高中数学苏教版(2022春 )选择性必修第二册 模块综合试卷(二) (word版含解析)
文档属性
| 名称 | 高中数学苏教版(2022春 )选择性必修第二册 模块综合试卷(二) (word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 478.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-21 11:20:08 | ||
图片预览




文档简介
高中数学苏教版(2022春 )选择性必修第二册 模块综合试卷(二)
(时间:120分钟 满分:150分)
一、单项选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.如图在平行六面体ABCD-A1B1C1D1中,E为A1D1的中点,设=a,=b,=c,则等于( )
A.-a-b+c
B.a-b+c
C.a-b-c
D.a+b-c
2.小明同学从8道概率题和2道排列题中选3道题进行测试,则他至少选中1道排列题的选法有( )
A.56 B.64 C.72 D.144
3.向量a=(2,4,x),b=(2,y,2),若|a|=6,且a⊥b,则x+y的值为( )
A.-3 B.1 C.-3或1 D.3或1
4.为了提升全民身体素质,学校十分重视学生体育锻炼,某校篮球运动员进行投篮练习.如果他前一球投进则后一球投进的概率为;如果他前一球投不进则后一球投进的概率为.若他第1球投进的概率为,则他第2球投进的概率为( )
A. B. C. D.
5.《易·系辞上》有“河出图,洛出书”之说,河图、洛书是中华文化,阴阳术数之源,其中河图排列结构是一、六在后,二、七在前,三、八在左,四、九在右,五、十背中.如图,白圈为阳数,黑点为阴数.若从这10个数中任取3个数,则这3个数中至少有2个阳数的概率为( )
A. B. C. D.
6.二项式(1+x)2+(1+x)3+…+(1+x)20的展开式中,含x2项的系数为( )
A.1 140 B.1 330 C.190 D.210
7.我省高考总成绩由语文、数学、外语三门统考科目和思想政治、历史、地理、物理、化学、生物六门选考科目组成,将每门选考科目的考生原始成绩从高到低划分为A,B+,B,C+,C,D+,D,E共8个等级,参照正态分布原则,确定各等级人数所占比例分别为3%,7%,16%,24%,24%,16%,7%,3%,选考科目成绩计入考生总成绩时,将A至E等级内的考生原始成绩,依照等比例转换法则,分别转换到[91,100],[81,90],[71,80],[61,70],[51,60],[41,50],[31,40],[21,30]八个分数区间,得到考生的等级成绩,如果某次高考模拟考试物理科目的原始成绩X~N(50,256),那么D等级的原始分最高大约为( )
附:①若X~N(μ,σ2),Y=,则Y~N(0,1);
②当Y~N(0,1)时,P(Y≤1.3)≈0.9.
A.23 B.29 C.36 D.43
8.如图是某地区2010年至2019年污染天数y(单位:天)与年份x的折线图.根据2010年至2014年数据,2015年至2019年的数据,2010年至2019年的数据分别建立线性回归模型y=b1x+a1,y=b2x+a2,y=b3x+a3,则( )
A.b1<b2<b3,a1<a2<a3
B.b1<b3<b2,a1<a3<a2
C.b2<b3<b1,a1<a3<a2
D.b2<b3<b1,a3<a2<a1
二、多项选择题(本大题共4小题,每小题5分,共20分.全部选对的得5分,部分选对的得2分,有选错的得0分)
9.已知随机变量X的概率分布如下,且E(X)=2,则下列说法正确的是( )
X 1 2 3
P m n
A.m=,n= B.m=,n=
C.D(X)= D.D(X)=
10.已知空间中三点A(0,1,0),B(2,2,0),C(-1,3,1),则下列说法正确的是( )
A.与是共线向量
B.与同向的单位向量是
C.和夹角的余弦值是
D.平面ABC的一个法向量是(1,-2,5)
11.为吸引顾客,某商场举办购物抽奖活动,抽奖规则是:从装有2个白球和3个红球(小球除颜色外,完全相同)的抽奖箱中,每次摸出一个球,不放回地依次摸取两次,记为一次抽奖.若摸出的2个球颜色相同则为中奖,否则为不中奖.则下列随机事件的概率正确的是( )
A.某顾客抽奖一次中奖的概率是
B.某顾客抽奖三次,至少有一次中奖的概率是
C.在一次抽奖过程中,若已知顾客第一次抽出了红球,则该顾客中奖的概率是
D.在一次抽奖过程中,若已知顾客第一次抽出了红球,则该顾客中奖的概率是
12.已知6的展开式中各项系数的和为2,则下列结论正确的有( )
A.a=1
B.展开式中常数项为160
C.展开式系数的绝对值的和为1 458
D.若r为偶数,则展开式中xr和xr-1的系数相等
三、填空题(本大题共4小题,每小题5分,共20分)
13.某产品的广告费用x与销售额y的统计数据如下表:
广告费用x(万元) 4 2 3 5
销售额y(万元) 49 26 39 54
根据上表可得线性回归方程y=x+中的为9.4,则=________,据此模型预报广告费用为6万元时销售额为________万元.
14.已知平面α的一个法向量为n=(1,-1,0),则y轴与平面α所成的角的大小为________.
15.5的展开式中常数项是________.
16.如图所示,在直平行六面体ABCD-A1B1C1D1中,BD⊥DC,BD=DC=1,点E在AA1上,且AE=AA1=,则点B到平面EDC1的距离为________.
四、解答题(本大题共6小题,共70分)
17.(10分)已知在n的展开式中,________.(填写条件前的序号)
条件①第5项的系数与第3项的系数之比是14∶3;
条件②第2项与倒数第3项的二项式系数之和为55;
条件③C-C=10.
(1)求展开式中二项式系数最大的项;
(2)求展开式中含x5的项.
18.(12分)某医院有2名女医生,3名男医生,3名女护士,1名男护士报名参加某研讨会,医院计划从医生和护士中各选2名参加.
(1)求选出的4名全是女性的方法数;
(2)记X为选出的4名参加者中男性的人数,求X的概率分布和均值.
19.(12分)在传染病学中,通常把从致病刺激物侵入机体或者对机体发生作用起,到机体出现反应或开始呈现该疾病对应的相关症状的这一阶段称为潜伏期.一研究团队统计了某地区200名患者的相关信息,得到如下表格:
潜伏期(单位:天) [0,2] (2,4] (4,6] (6,8] (8,10] (10,12] (12,14]
人数 17 43 60 50 26 3 1
(1)该传染病的潜伏期受诸多因素的影响,为研究潜伏期与患者年龄的关系,根据上表数据将如下列联表补充完整,并根据列联表判断是否有99%的把握认为该传染病的潜伏期与患者年龄有关.
潜伏期≤6天 潜伏期>6天 合计
50岁以上
(含50岁) 100
50岁以下 55
合计 200
(2)将200名患者的潜伏期超过6天的频率视为该地区每名患者潜伏期超过6天发生的概率,每名患者的潜伏期是否超过6天相互独立.为了深入研究,该团队随机调查了该地区20名患者,其中潜伏期超过6天的人数为X,求随机变量X的均值和方差.
附:
P(χ2≥x0) 0.05 0.025 0.010
x0 3.841 5.024 6.635
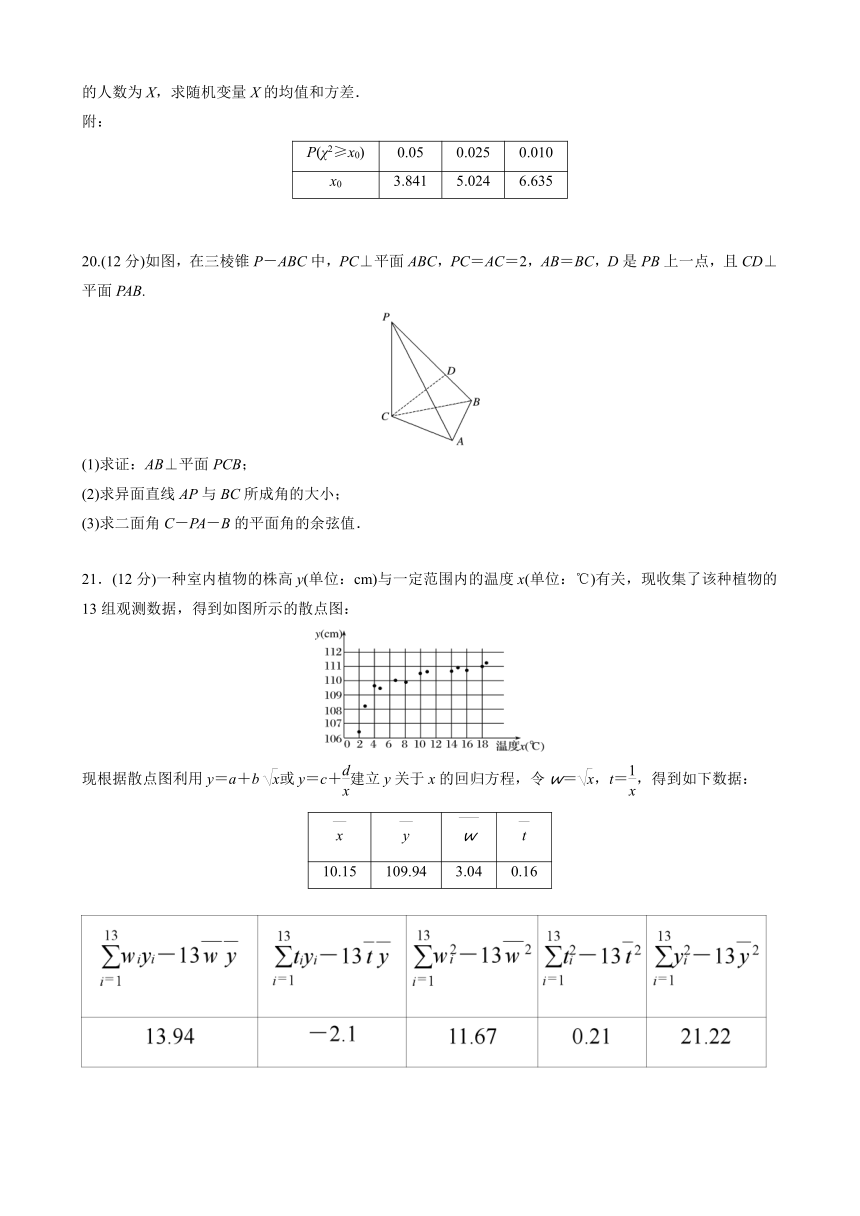
20.(12分)如图,在三棱锥P-ABC中,PC⊥平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD⊥平面PAB.
(1)求证:AB⊥平面PCB;
(2)求异面直线AP与BC所成角的大小;
(3)求二面角C-PA-B的平面角的余弦值.
21.(12分)一种室内植物的株高y(单位:cm)与一定范围内的温度x(单位:℃)有关,现收集了该种植物的13组观测数据,得到如图所示的散点图:
现根据散点图利用y=a+b或y=c+建立y关于x的回归方程,令w=,t=,得到如下数据:
10.15 109.94 3.04 0.16
且(wi,yi)与(ti,yi)(i=1,2,3,…,13)的相关系数分别为r1,r2,其中r1=0.885 9.
(1)用相关系数说明哪种模型建立y关于x的回归方程更合适;
(2)①根据(1)的结果及表中数据,求y关于x的回归方程;
②已知这种植物的利润z(单位:千元)与x,y的关系为z=10y-x,当x为何值时,利润的值最大.
附:对于样本(ui,Di)(i=1,2,…,n),其回归直线=u+的斜率和截距的最小二乘法估计公式分别为:
≈2.11.
22.(12分)当今世界环境污染已经成为各国面临的一大难题,其中大气污染是目前城市急需应对的一项课题.某市号召市民尽量减少开车出行以绿色低碳的出行方式支持节能减排.原来天天开车上班的王先生积极响应政府号召,准备每天从骑自行车和开车两种出行方式中随机选择一种方式出行.从即日起出行方式选择规则如下:第一天选择骑自行车方式上班,随后每天用“一次性抛掷4枚均匀硬币”的方法确定出行方式,若得到的正面朝上的枚数小于3,则该天出行方式与前一天相同,否则选择另一种出行方式.
(1)求王先生前三天骑自行车上班的天数X的概率分布;
(2)设Pn(n∈N)表示事件“第n天王先生上班选择的是骑自行车出行方式”的概率.
①用Pn-1表示Pn(n≥2);
②请问王先生的这种选择随机选择出行方式有没有积极响应该市政府的号召?请说明理由.
答案与解析
高中数学苏教版(2022春 )选择性必修第二册 模块综合试卷(二)
(时间:120分钟 满分:150分)
一、单项选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.如图在平行六面体ABCD-A1B1C1D1中,E为A1D1的中点,设=a,=b,=c,则等于( )
A.-a-b+c
B.a-b+c
C.a-b-c
D.a+b-c
答案 A
解析 由题意结合平行六面体的性质可得
=++=++
=--=-a-b+c,故选A.
2.小明同学从8道概率题和2道排列题中选3道题进行测试,则他至少选中1道排列题的选法有( )
A.56 B.64 C.72 D.144
答案 B
解析 从8道概率题和2道排列题中选3道题进行测试,至少选中1道排列题的选法有CC+CC=+8=64.故选B.
3.向量a=(2,4,x),b=(2,y,2),若|a|=6,且a⊥b,则x+y的值为( )
A.-3 B.1 C.-3或1 D.3或1
答案 C
解析 由题意得=6,4+4y+2x=0,
解得或则x+y=-3或1.
4.为了提升全民身体素质,学校十分重视学生体育锻炼,某校篮球运动员进行投篮练习.如果他前一球投进则后一球投进的概率为;如果他前一球投不进则后一球投进的概率为.若他第1球投进的概率为,则他第2球投进的概率为( )
A. B. C. D.
答案 B
解析 记事件A为“第1球投进”,事件B为“第2球投进”,P(B|A)=,P(B|)=,P(A)=,
由全概率公式可得P(B)=P(A)P(B|A)+P()P(B|)=2+2=.
5.《易·系辞上》有“河出图,洛出书”之说,河图、洛书是中华文化,阴阳术数之源,其中河图排列结构是一、六在后,二、七在前,三、八在左,四、九在右,五、十背中.如图,白圈为阳数,黑点为阴数.若从这10个数中任取3个数,则这3个数中至少有2个阳数的概率为( )
A. B. C. D.
答案 C
解析 由题意可知,10个数中,1,3,5,7,9是阳数,2,4,6,8,10是阴数,
若任取3个数中有2个阳数,则P===,
若任取3个数中有3个阳数,则P===,
故这3个数中至少有2个阳数的概率
P=+=,故选C.
6.二项式(1+x)2+(1+x)3+…+(1+x)20的展开式中,含x2项的系数为( )
A.1 140 B.1 330 C.190 D.210
答案 B
解析 根据二项式定理得(1+x)2+(1+x)3+…+(1+x)20的展开式中,含x2项的系数为:
C+C+C+…+C=C+C+C+…+C
=C+C+…+C=…=C+C=C=1 330.故选B.
7.我省高考总成绩由语文、数学、外语三门统考科目和思想政治、历史、地理、物理、化学、生物六门选考科目组成,将每门选考科目的考生原始成绩从高到低划分为A,B+,B,C+,C,D+,D,E共8个等级,参照正态分布原则,确定各等级人数所占比例分别为3%,7%,16%,24%,24%,16%,7%,3%,选考科目成绩计入考生总成绩时,将A至E等级内的考生原始成绩,依照等比例转换法则,分别转换到[91,100],[81,90],[71,80],[61,70],[51,60],[41,50],[31,40],[21,30]八个分数区间,得到考生的等级成绩,如果某次高考模拟考试物理科目的原始成绩X~N(50,256),那么D等级的原始分最高大约为( )
附:①若X~N(μ,σ2),Y=,则Y~N(0,1);
②当Y~N(0,1)时,P(Y≤1.3)≈0.9.
A.23 B.29 C.36 D.43
答案 B
解析 由题意知,X~N(50,256),则有μ=50,σ=16,设D等级的原始分最高大约为x,对应的等级分为40,而P(等级分≥40)=1-(7%+3%)=0.9,
∴有P=0.9,
而P(Y≤1.3)≈0.9,由对称性知P(Y≥-1.3)≈0.9,
∴有=-1.3,即x=29.2≈29,故选B.
8.如图是某地区2010年至2019年污染天数y(单位:天)与年份x的折线图.根据2010年至2014年数据,2015年至2019年的数据,2010年至2019年的数据分别建立线性回归模型y=b1x+a1,y=b2x+a2,y=b3x+a3,则( )
A.b1<b2<b3,a1<a2<a3
B.b1<b3<b2,a1<a3<a2
C.b2<b3<b1,a1<a3<a2
D.b2<b3<b1,a3<a2<a1
答案 C
解析 2010年至2014年数据,2015年至2019年的数据,2010年至2019年的数据的回归模型分别为l1:y=b1x+a1,l2:y=b2x+a2,l3:y=b3x+a3,
∴由图知:2010年至2014年数据为71,66,68,63,65;
2015年至2019年数据为57,40,32,16,6;
2010年至2019年数据为71,66,68,63,65,57,40,32,16,6;
均成递减趋势,
又1==66.6,
2==30.2,
3==48.4,且极差分别为8,51,65,三条回归方程的直线大致图象,如图所示.
∴回归方程的斜率大小关系为b2a3>a1>0.故选C.
二、多项选择题(本大题共4小题,每小题5分,共20分.全部选对的得5分,部分选对的得2分,有选错的得0分)
9.已知随机变量X的概率分布如下,且E(X)=2,则下列说法正确的是( )
X 1 2 3
P m n
A.m=,n= B.m=,n=
C.D(X)= D.D(X)=
答案 BC
解析 依题意
E(X)=1·m+2·n+3×=m+2n+1=2,
所以m+2n=1,结合m+n+=1,
解得m=n=,所以B选项正确.
D(X)=(1-2)2×+(2-2)2×+(3-2)2×=,
所以C选项正确.故选BC.
10.已知空间中三点A(0,1,0),B(2,2,0),C(-1,3,1),则下列说法正确的是( )
A.与是共线向量
B.与同向的单位向量是
C.和夹角的余弦值是
D.平面ABC的一个法向量是(1,-2,5)
答案 BD
解析 对于A,=(2,1,0),=(-1,2,1),
可知≠λ,与不共线,A错误;
对于B,∵=(2,1,0),
∴||=,
∴=,即与同向的单位向量是,B正确;
对于C,∵=(-3,1,1),
∴cos〈,〉===-,
即和夹角的余弦值为-,C错误;
对于D,设平面ABC的法向量n=(x,y,z),
则
令x=1,解得y=-2,z=5,
∴n=(1,-2,5),
即平面ABC的一个法向量为(1,-2,5),D正确,
故选BD.
11.为吸引顾客,某商场举办购物抽奖活动,抽奖规则是:从装有2个白球和3个红球(小球除颜色外,完全相同)的抽奖箱中,每次摸出一个球,不放回地依次摸取两次,记为一次抽奖.若摸出的2个球颜色相同则为中奖,否则为不中奖.则下列随机事件的概率正确的是( )
A.某顾客抽奖一次中奖的概率是
B.某顾客抽奖三次,至少有一次中奖的概率是
C.在一次抽奖过程中,若已知顾客第一次抽出了红球,则该顾客中奖的概率是
D.在一次抽奖过程中,若已知顾客第一次抽出了红球,则该顾客中奖的概率是
答案 ABD
解析 顾客抽奖一次中奖的概率为==,故A选项正确;
顾客抽奖三次,至少有一次中奖的概率是1-3=1-3=1-=,故B选项正确;
对于C,D选项,由于第一次抽出了红球,故剩余2个白球和2个红球,再抽一个,抽到红球的概率是=,故C选项错误,D选项正确.
12.已知6的展开式中各项系数的和为2,则下列结论正确的有( )
A.a=1
B.展开式中常数项为160
C.展开式系数的绝对值的和为1 458
D.若r为偶数,则展开式中xr和xr-1的系数相等
答案 ACD
解析 令x=1,可得6的展开式中各项系数的和为(1+a)×1=2,∴a=1,故选项A正确;
∵6=(64x6-192x4+240x2-160+60x-2-12x-4+x-6),故展开式中常数项为-160,故选项B不正确;
6的展开式中各项系数绝对值的和,即6的展开式中各项系数和,
为(1+a)·36=1 458,故选项C正确;
根据6=(64x6-192x4+240x2-160+60x-2-12x-4+x-6)
=64x6-192x4+240x2-160+60x-2-12x-4+x-6+64x5-192x3+240x-+60x-3-12x-5+x-7可得若r为偶数,则展开式中xr和xr-1的系数相等,故选项D正确,故选ACD.
三、填空题(本大题共4小题,每小题5分,共20分)
13.某产品的广告费用x与销售额y的统计数据如下表:
广告费用x(万元) 4 2 3 5
销售额y(万元) 49 26 39 54
根据上表可得线性回归方程y=x+中的为9.4,则=________,据此模型预报广告费用为6万元时销售额为________万元.
答案 9.1 65.5
解析 样本点的中心是(3.5,42),
则=42-9.4×3.5=9.1,
所以线性回归方程是=9.4x+9.1,
把x=6代入得y=65.5.
14.已知平面α的一个法向量为n=(1,-1,0),则y轴与平面α所成的角的大小为________.
答案
解析 y轴的一个方向向量为s=(0,1,0),
cos〈n,s〉==-,
即y轴与平面α所成角的正弦值是,故其所成的角的大小是.
15.5的展开式中常数项是________.
答案 -161
解析 5表示五个相乘,则展开式中的常数项由三种情况产生,
第一种是从五个中分别抽取2x,2x,,,-1,则此时的常数项为C·C·22·(-1)=-120,
第二种情况是从五个中都抽取-1,则此时的常数项为(-1)5=-1,
第三种情况是从五个中分别抽取2x,,-1,-1,-1,
则此时的常数项为C·C·21·(-1)3=-40,
则展开式中常数项为-120-1-40=-161.
16.如图所示,在直平行六面体ABCD-A1B1C1D1中,BD⊥DC,BD=DC=1,点E在AA1上,且AE=AA1=,则点B到平面EDC1的距离为________.
答案
解析 建立如图所示的空间直角坐标系,
则D(0,0,0),A(1,-1,0),B(1,0,0),C(0,1,0),C1(0,1,2),E,
∴=(0,1,2),=.
设平面EDC1的法向量为n=(x,y,z),
则
令z=1,则x=-,y=-2,
∴n=.
∴点B到平面EDC1的距离
d===.
四、解答题(本大题共6小题,共70分)
17.(10分)已知在n的展开式中,________.(填写条件前的序号)
条件①第5项的系数与第3项的系数之比是14∶3;
条件②第2项与倒数第3项的二项式系数之和为55;
条件③C-C=10.
(1)求展开式中二项式系数最大的项;
(2)求展开式中含x5的项.
解 通项公式为
Tr+1=C()n-rr=(-1)rC,
r=0,1,2,…,n.
若填条件①,
(1)依题意得=,即3C=14C,
整理得(n-10)(n+5)=0,
所以n=10或n=-5(舍),
因为n=10,所以10的展开式共有11项,
所以展开式中二项式系数最大的项是第6项,
所以T6=T5+1=(-1)5C
(2)通项公式为Tr+1=(-1)rC,
令=5,得r=0,
所以展开式中含x5的项为x5.
若填条件②,
(1)依题意得C+C=55,
所以n+C=55,
所以n+=55,
即n2+n-110=0,
所以n=10或n=-11(舍),
因为n=10,所以10的展开式共有11项,
所以展开式中二项式系数最大的项是第6项,
所以T6=T5+1=(-1)5C
(2)通项公式为Tr+1=(-1)rC,
令=5,得r=0,
所以展开式中含x5的项为x5.
若填条件③,
(1)依题意得C-C=10,
则C-C=10,
所以-=10,
所以n=10,
因为n=10,所以10的展开式共有11项,
所以展开式中二项式系数最大的项是第6项,
所以T6=T5+1=(-1)5C
(2)通项公式为Tr+1=(-1)rC,
令=5,得r=0,所以展开式中含x5的项为x5.
18.(12分)某医院有2名女医生,3名男医生,3名女护士,1名男护士报名参加某研讨会,医院计划从医生和护士中各选2名参加.
(1)求选出的4名全是女性的方法数;
(2)记X为选出的4名参加者中男性的人数,求X的概率分布和均值.
解 (1)从2名女医生中选2人有C种选法,从3名女护士中选2人有C种选法,则选出的4名全是女性有C·C=3(种)不同的选法.
(2)X的取值可能为0,1,2,3.
P(X=0)==,
P(X=1)==,
P(X=2)==,
P(X=3)==,
列表如下:
X 0 1 2 3
P
∴E(X)=0×+1×+2×+3×=.
19.(12分)在传染病学中,通常把从致病刺激物侵入机体或者对机体发生作用起,到机体出现反应或开始呈现该疾病对应的相关症状的这一阶段称为潜伏期.一研究团队统计了某地区200名患者的相关信息,得到如下表格:
潜伏期(单位:天) [0,2] (2,4] (4,6] (6,8] (8,10] (10,12] (12,14]
人数 17 43 60 50 26 3 1
(1)该传染病的潜伏期受诸多因素的影响,为研究潜伏期与患者年龄的关系,根据上表数据将如下列联表补充完整,并根据列联表判断是否有99%的把握认为该传染病的潜伏期与患者年龄有关.
潜伏期≤6天 潜伏期>6天 合计
50岁以上
(含50岁) 100
50岁以下 55
合计 200
(2)将200名患者的潜伏期超过6天的频率视为该地区每名患者潜伏期超过6天发生的概率,每名患者的潜伏期是否超过6天相互独立.为了深入研究,该团队随机调查了该地区20名患者,其中潜伏期超过6天的人数为X,求随机变量X的均值和方差.
附:
P(χ2≥x0) 0.05 0.025 0.010
x0 3.841 5.024 6.635
解 (1)由题意得列联表:
潜伏期≤6天 潜伏期>6天 合计
50岁以上
(含50岁) 75 25 100
50岁以下 45 55 100
合计 120 80 200
由上表可得
χ2==18.75>6.635,所以有99%的把握认为该传染病的潜伏期与患者年龄有关.
(2)由题意可知,一名患者潜伏期超过6天的概率为
P==,故X~B,
∴E(X)=20×=8,D(X)=20××=.
20.(12分)如图,在三棱锥P-ABC中,PC⊥平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD⊥平面PAB.
(1)求证:AB⊥平面PCB;
(2)求异面直线AP与BC所成角的大小;
(3)求二面角C-PA-B的平面角的余弦值.
(1)证明 ∵PC⊥平面ABC,AB 平面ABC,
∴PC⊥AB.
∵CD⊥平面PAB,AB 平面PAB,
∴CD⊥AB.
又PC∩CD=C,PC,CD 平面PCB,
∴AB⊥平面PCB.
(2)解 由(1)知AB⊥平面PCB,
∴AB⊥BC.
∵PC=AC=2,AB=BC,
∴BC=AB=.
如图,以B为坐标原点,建立空间直角坐标系,则B(0,0,0),A(0,,0),C(,0,0),P(,0,2),
∴=(,-,2),=(,0,0),
则·=×+0+0=2,
∴cos〈,〉===,
故异面直线AP与BC所成的角为.
(3)解 结合(2)中建立的空间直角坐标系,设平面PAB的法向量为m=(x1,y1,z1).
易知=(0,-,0),=(,-,2).
由
得
令z1=-1,得x1=,y1=0,
∴平面PAB的一个法向量为m=(,0,-1).
设平面PAC的法向量为n=(x2,y2,z2).
易知=(0,0,-2),=(,-,0).
由
得令x2=1,得y2=1,z2=0,
∴平面PAC的一个法向量为n=(1,1,0).
∴cos〈m,n〉===.
由图知,二面角C-PA-B的平面角为钝角,
∴二面角C-PA-B的平面角的余弦值为-.
21.(12分)一种室内植物的株高y(单位:cm)与一定范围内的温度x(单位:℃)有关,现收集了该种植物的13组观测数据,得到如图所示的散点图:
现根据散点图利用y=a+b或y=c+建立y关于x的回归方程,令w=,t=,得到如下数据:
10.15 109.94 3.04 0.16
iyi-13 iyi-13 -132 -132 -132
13.94 -2.1 11.67 0.21 21.22
且(wi,yi)与(ti,yi)(i=1,2,3,…,13)的相关系数分别为r1,r2,其中r1=0.885 9.
(1)用相关系数说明哪种模型建立y关于x的回归方程更合适;
(2)①根据(1)的结果及表中数据,求y关于x的回归方程;
②已知这种植物的利润z(单位:千元)与x,y的关系为z=10y-x,当x为何值时,利润的值最大.
附:对于样本(ui,Di)(i=1,2,…,n),其回归直线=u+的斜率和截距的最小二乘法估计公式分别为:
解 (1)由相关系数公式可得
=-≈-≈-0.995 3,
因为|r1|<|r2|<1,
所以用y=c+模型建立y与x的回归方程更合适.
(2)
①
=-=109.94-(-10)×0.16=111.54,
因此,y关于x的回归方程为=111.54-.
②由题意知z=10y-x=10×-x
=1 115.4-,
由基本不等式可得+x≥2=20,
所以z≤1 115.4-20=1 095.4,
当且仅当x=10时等号成立,所以当温度为10 ℃时,这种植物的利润z的值最大.
22.(12分)当今世界环境污染已经成为各国面临的一大难题,其中大气污染是目前城市急需应对的一项课题.某市号召市民尽量减少开车出行以绿色低碳的出行方式支持节能减排.原来天天开车上班的王先生积极响应政府号召,准备每天从骑自行车和开车两种出行方式中随机选择一种方式出行.从即日起出行方式选择规则如下:第一天选择骑自行车方式上班,随后每天用“一次性抛掷4枚均匀硬币”的方法确定出行方式,若得到的正面朝上的枚数小于3,则该天出行方式与前一天相同,否则选择另一种出行方式.
(1)求王先生前三天骑自行车上班的天数X的概率分布;
(2)设Pn(n∈N)表示事件“第n天王先生上班选择的是骑自行车出行方式”的概率.
①用Pn-1表示Pn(n≥2);
②请问王先生的这种选择随机选择出行方式有没有积极响应该市政府的号召?请说明理由.
解 (1)设一次性抛掷4枚均匀的硬币得到正面向上的枚数为ξ,则ξ~B,
P(ξ<3)=C4+C4+C4=,
P(ξ≥3)=1-P(ξ<3)=,
由已知随机变量X的可能取值为1,2,3;
P(X=1)=P(ξ≥3)·P(ξ<3)=×=;
P(X=2)=P(ξ<3)·P(ξ≥3)+P(ξ≥3)·P(ξ≥3)
=×+×=;
P(X=3)=P(ξ<3)·P(ξ<3)=×=.
所以随机变量X的概率分布为
X 1 2 3
P
(2)①设An-1表示事件“第n-1天王先生选择的是骑自行车出行方式”,An表示事件“第n天王先生选择的是骑自行车出行方式”,由全概率公式知
Pn=P(An)=P(An|An-1)P(An-1)+P(An|)P()
=Pn-1·P(ξ<3)+(1-Pn-1)·P(ξ≥3)
=Pn-1+(1-Pn-1)=Pn-1+,
所以Pn=Pn-1+(n≥2).
②由①知Pn-=,n≥2,
又P1=1,所以数列是首项为,公比为的等比数列,所以Pn-=n-1,Pn
=n-1+.
因为Pn=n-1+>恒成立,所以王先生每天选择骑自行车出行方式的概率始终大于选择开车出行方式,从长期来看,王先生选择骑自行车出行方式的次数多于选择开车出行方式的次数是大概率事件,所以王先生积极响应该市政府的号召.
(时间:120分钟 满分:150分)
一、单项选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.如图在平行六面体ABCD-A1B1C1D1中,E为A1D1的中点,设=a,=b,=c,则等于( )
A.-a-b+c
B.a-b+c
C.a-b-c
D.a+b-c
2.小明同学从8道概率题和2道排列题中选3道题进行测试,则他至少选中1道排列题的选法有( )
A.56 B.64 C.72 D.144
3.向量a=(2,4,x),b=(2,y,2),若|a|=6,且a⊥b,则x+y的值为( )
A.-3 B.1 C.-3或1 D.3或1
4.为了提升全民身体素质,学校十分重视学生体育锻炼,某校篮球运动员进行投篮练习.如果他前一球投进则后一球投进的概率为;如果他前一球投不进则后一球投进的概率为.若他第1球投进的概率为,则他第2球投进的概率为( )
A. B. C. D.
5.《易·系辞上》有“河出图,洛出书”之说,河图、洛书是中华文化,阴阳术数之源,其中河图排列结构是一、六在后,二、七在前,三、八在左,四、九在右,五、十背中.如图,白圈为阳数,黑点为阴数.若从这10个数中任取3个数,则这3个数中至少有2个阳数的概率为( )
A. B. C. D.
6.二项式(1+x)2+(1+x)3+…+(1+x)20的展开式中,含x2项的系数为( )
A.1 140 B.1 330 C.190 D.210
7.我省高考总成绩由语文、数学、外语三门统考科目和思想政治、历史、地理、物理、化学、生物六门选考科目组成,将每门选考科目的考生原始成绩从高到低划分为A,B+,B,C+,C,D+,D,E共8个等级,参照正态分布原则,确定各等级人数所占比例分别为3%,7%,16%,24%,24%,16%,7%,3%,选考科目成绩计入考生总成绩时,将A至E等级内的考生原始成绩,依照等比例转换法则,分别转换到[91,100],[81,90],[71,80],[61,70],[51,60],[41,50],[31,40],[21,30]八个分数区间,得到考生的等级成绩,如果某次高考模拟考试物理科目的原始成绩X~N(50,256),那么D等级的原始分最高大约为( )
附:①若X~N(μ,σ2),Y=,则Y~N(0,1);
②当Y~N(0,1)时,P(Y≤1.3)≈0.9.
A.23 B.29 C.36 D.43
8.如图是某地区2010年至2019年污染天数y(单位:天)与年份x的折线图.根据2010年至2014年数据,2015年至2019年的数据,2010年至2019年的数据分别建立线性回归模型y=b1x+a1,y=b2x+a2,y=b3x+a3,则( )
A.b1<b2<b3,a1<a2<a3
B.b1<b3<b2,a1<a3<a2
C.b2<b3<b1,a1<a3<a2
D.b2<b3<b1,a3<a2<a1
二、多项选择题(本大题共4小题,每小题5分,共20分.全部选对的得5分,部分选对的得2分,有选错的得0分)
9.已知随机变量X的概率分布如下,且E(X)=2,则下列说法正确的是( )
X 1 2 3
P m n
A.m=,n= B.m=,n=
C.D(X)= D.D(X)=
10.已知空间中三点A(0,1,0),B(2,2,0),C(-1,3,1),则下列说法正确的是( )
A.与是共线向量
B.与同向的单位向量是
C.和夹角的余弦值是
D.平面ABC的一个法向量是(1,-2,5)
11.为吸引顾客,某商场举办购物抽奖活动,抽奖规则是:从装有2个白球和3个红球(小球除颜色外,完全相同)的抽奖箱中,每次摸出一个球,不放回地依次摸取两次,记为一次抽奖.若摸出的2个球颜色相同则为中奖,否则为不中奖.则下列随机事件的概率正确的是( )
A.某顾客抽奖一次中奖的概率是
B.某顾客抽奖三次,至少有一次中奖的概率是
C.在一次抽奖过程中,若已知顾客第一次抽出了红球,则该顾客中奖的概率是
D.在一次抽奖过程中,若已知顾客第一次抽出了红球,则该顾客中奖的概率是
12.已知6的展开式中各项系数的和为2,则下列结论正确的有( )
A.a=1
B.展开式中常数项为160
C.展开式系数的绝对值的和为1 458
D.若r为偶数,则展开式中xr和xr-1的系数相等
三、填空题(本大题共4小题,每小题5分,共20分)
13.某产品的广告费用x与销售额y的统计数据如下表:
广告费用x(万元) 4 2 3 5
销售额y(万元) 49 26 39 54
根据上表可得线性回归方程y=x+中的为9.4,则=________,据此模型预报广告费用为6万元时销售额为________万元.
14.已知平面α的一个法向量为n=(1,-1,0),则y轴与平面α所成的角的大小为________.
15.5的展开式中常数项是________.
16.如图所示,在直平行六面体ABCD-A1B1C1D1中,BD⊥DC,BD=DC=1,点E在AA1上,且AE=AA1=,则点B到平面EDC1的距离为________.
四、解答题(本大题共6小题,共70分)
17.(10分)已知在n的展开式中,________.(填写条件前的序号)
条件①第5项的系数与第3项的系数之比是14∶3;
条件②第2项与倒数第3项的二项式系数之和为55;
条件③C-C=10.
(1)求展开式中二项式系数最大的项;
(2)求展开式中含x5的项.
18.(12分)某医院有2名女医生,3名男医生,3名女护士,1名男护士报名参加某研讨会,医院计划从医生和护士中各选2名参加.
(1)求选出的4名全是女性的方法数;
(2)记X为选出的4名参加者中男性的人数,求X的概率分布和均值.
19.(12分)在传染病学中,通常把从致病刺激物侵入机体或者对机体发生作用起,到机体出现反应或开始呈现该疾病对应的相关症状的这一阶段称为潜伏期.一研究团队统计了某地区200名患者的相关信息,得到如下表格:
潜伏期(单位:天) [0,2] (2,4] (4,6] (6,8] (8,10] (10,12] (12,14]
人数 17 43 60 50 26 3 1
(1)该传染病的潜伏期受诸多因素的影响,为研究潜伏期与患者年龄的关系,根据上表数据将如下列联表补充完整,并根据列联表判断是否有99%的把握认为该传染病的潜伏期与患者年龄有关.
潜伏期≤6天 潜伏期>6天 合计
50岁以上
(含50岁) 100
50岁以下 55
合计 200
(2)将200名患者的潜伏期超过6天的频率视为该地区每名患者潜伏期超过6天发生的概率,每名患者的潜伏期是否超过6天相互独立.为了深入研究,该团队随机调查了该地区20名患者,其中潜伏期超过6天的人数为X,求随机变量X的均值和方差.
附:
P(χ2≥x0) 0.05 0.025 0.010
x0 3.841 5.024 6.635
20.(12分)如图,在三棱锥P-ABC中,PC⊥平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD⊥平面PAB.
(1)求证:AB⊥平面PCB;
(2)求异面直线AP与BC所成角的大小;
(3)求二面角C-PA-B的平面角的余弦值.
21.(12分)一种室内植物的株高y(单位:cm)与一定范围内的温度x(单位:℃)有关,现收集了该种植物的13组观测数据,得到如图所示的散点图:
现根据散点图利用y=a+b或y=c+建立y关于x的回归方程,令w=,t=,得到如下数据:
10.15 109.94 3.04 0.16
且(wi,yi)与(ti,yi)(i=1,2,3,…,13)的相关系数分别为r1,r2,其中r1=0.885 9.
(1)用相关系数说明哪种模型建立y关于x的回归方程更合适;
(2)①根据(1)的结果及表中数据,求y关于x的回归方程;
②已知这种植物的利润z(单位:千元)与x,y的关系为z=10y-x,当x为何值时,利润的值最大.
附:对于样本(ui,Di)(i=1,2,…,n),其回归直线=u+的斜率和截距的最小二乘法估计公式分别为:
≈2.11.
22.(12分)当今世界环境污染已经成为各国面临的一大难题,其中大气污染是目前城市急需应对的一项课题.某市号召市民尽量减少开车出行以绿色低碳的出行方式支持节能减排.原来天天开车上班的王先生积极响应政府号召,准备每天从骑自行车和开车两种出行方式中随机选择一种方式出行.从即日起出行方式选择规则如下:第一天选择骑自行车方式上班,随后每天用“一次性抛掷4枚均匀硬币”的方法确定出行方式,若得到的正面朝上的枚数小于3,则该天出行方式与前一天相同,否则选择另一种出行方式.
(1)求王先生前三天骑自行车上班的天数X的概率分布;
(2)设Pn(n∈N)表示事件“第n天王先生上班选择的是骑自行车出行方式”的概率.
①用Pn-1表示Pn(n≥2);
②请问王先生的这种选择随机选择出行方式有没有积极响应该市政府的号召?请说明理由.
答案与解析
高中数学苏教版(2022春 )选择性必修第二册 模块综合试卷(二)
(时间:120分钟 满分:150分)
一、单项选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.如图在平行六面体ABCD-A1B1C1D1中,E为A1D1的中点,设=a,=b,=c,则等于( )
A.-a-b+c
B.a-b+c
C.a-b-c
D.a+b-c
答案 A
解析 由题意结合平行六面体的性质可得
=++=++
=--=-a-b+c,故选A.
2.小明同学从8道概率题和2道排列题中选3道题进行测试,则他至少选中1道排列题的选法有( )
A.56 B.64 C.72 D.144
答案 B
解析 从8道概率题和2道排列题中选3道题进行测试,至少选中1道排列题的选法有CC+CC=+8=64.故选B.
3.向量a=(2,4,x),b=(2,y,2),若|a|=6,且a⊥b,则x+y的值为( )
A.-3 B.1 C.-3或1 D.3或1
答案 C
解析 由题意得=6,4+4y+2x=0,
解得或则x+y=-3或1.
4.为了提升全民身体素质,学校十分重视学生体育锻炼,某校篮球运动员进行投篮练习.如果他前一球投进则后一球投进的概率为;如果他前一球投不进则后一球投进的概率为.若他第1球投进的概率为,则他第2球投进的概率为( )
A. B. C. D.
答案 B
解析 记事件A为“第1球投进”,事件B为“第2球投进”,P(B|A)=,P(B|)=,P(A)=,
由全概率公式可得P(B)=P(A)P(B|A)+P()P(B|)=2+2=.
5.《易·系辞上》有“河出图,洛出书”之说,河图、洛书是中华文化,阴阳术数之源,其中河图排列结构是一、六在后,二、七在前,三、八在左,四、九在右,五、十背中.如图,白圈为阳数,黑点为阴数.若从这10个数中任取3个数,则这3个数中至少有2个阳数的概率为( )
A. B. C. D.
答案 C
解析 由题意可知,10个数中,1,3,5,7,9是阳数,2,4,6,8,10是阴数,
若任取3个数中有2个阳数,则P===,
若任取3个数中有3个阳数,则P===,
故这3个数中至少有2个阳数的概率
P=+=,故选C.
6.二项式(1+x)2+(1+x)3+…+(1+x)20的展开式中,含x2项的系数为( )
A.1 140 B.1 330 C.190 D.210
答案 B
解析 根据二项式定理得(1+x)2+(1+x)3+…+(1+x)20的展开式中,含x2项的系数为:
C+C+C+…+C=C+C+C+…+C
=C+C+…+C=…=C+C=C=1 330.故选B.
7.我省高考总成绩由语文、数学、外语三门统考科目和思想政治、历史、地理、物理、化学、生物六门选考科目组成,将每门选考科目的考生原始成绩从高到低划分为A,B+,B,C+,C,D+,D,E共8个等级,参照正态分布原则,确定各等级人数所占比例分别为3%,7%,16%,24%,24%,16%,7%,3%,选考科目成绩计入考生总成绩时,将A至E等级内的考生原始成绩,依照等比例转换法则,分别转换到[91,100],[81,90],[71,80],[61,70],[51,60],[41,50],[31,40],[21,30]八个分数区间,得到考生的等级成绩,如果某次高考模拟考试物理科目的原始成绩X~N(50,256),那么D等级的原始分最高大约为( )
附:①若X~N(μ,σ2),Y=,则Y~N(0,1);
②当Y~N(0,1)时,P(Y≤1.3)≈0.9.
A.23 B.29 C.36 D.43
答案 B
解析 由题意知,X~N(50,256),则有μ=50,σ=16,设D等级的原始分最高大约为x,对应的等级分为40,而P(等级分≥40)=1-(7%+3%)=0.9,
∴有P=0.9,
而P(Y≤1.3)≈0.9,由对称性知P(Y≥-1.3)≈0.9,
∴有=-1.3,即x=29.2≈29,故选B.
8.如图是某地区2010年至2019年污染天数y(单位:天)与年份x的折线图.根据2010年至2014年数据,2015年至2019年的数据,2010年至2019年的数据分别建立线性回归模型y=b1x+a1,y=b2x+a2,y=b3x+a3,则( )
A.b1<b2<b3,a1<a2<a3
B.b1<b3<b2,a1<a3<a2
C.b2<b3<b1,a1<a3<a2
D.b2<b3<b1,a3<a2<a1
答案 C
解析 2010年至2014年数据,2015年至2019年的数据,2010年至2019年的数据的回归模型分别为l1:y=b1x+a1,l2:y=b2x+a2,l3:y=b3x+a3,
∴由图知:2010年至2014年数据为71,66,68,63,65;
2015年至2019年数据为57,40,32,16,6;
2010年至2019年数据为71,66,68,63,65,57,40,32,16,6;
均成递减趋势,
又1==66.6,
2==30.2,
3==48.4,且极差分别为8,51,65,三条回归方程的直线大致图象,如图所示.
∴回归方程的斜率大小关系为b2
二、多项选择题(本大题共4小题,每小题5分,共20分.全部选对的得5分,部分选对的得2分,有选错的得0分)
9.已知随机变量X的概率分布如下,且E(X)=2,则下列说法正确的是( )
X 1 2 3
P m n
A.m=,n= B.m=,n=
C.D(X)= D.D(X)=
答案 BC
解析 依题意
E(X)=1·m+2·n+3×=m+2n+1=2,
所以m+2n=1,结合m+n+=1,
解得m=n=,所以B选项正确.
D(X)=(1-2)2×+(2-2)2×+(3-2)2×=,
所以C选项正确.故选BC.
10.已知空间中三点A(0,1,0),B(2,2,0),C(-1,3,1),则下列说法正确的是( )
A.与是共线向量
B.与同向的单位向量是
C.和夹角的余弦值是
D.平面ABC的一个法向量是(1,-2,5)
答案 BD
解析 对于A,=(2,1,0),=(-1,2,1),
可知≠λ,与不共线,A错误;
对于B,∵=(2,1,0),
∴||=,
∴=,即与同向的单位向量是,B正确;
对于C,∵=(-3,1,1),
∴cos〈,〉===-,
即和夹角的余弦值为-,C错误;
对于D,设平面ABC的法向量n=(x,y,z),
则
令x=1,解得y=-2,z=5,
∴n=(1,-2,5),
即平面ABC的一个法向量为(1,-2,5),D正确,
故选BD.
11.为吸引顾客,某商场举办购物抽奖活动,抽奖规则是:从装有2个白球和3个红球(小球除颜色外,完全相同)的抽奖箱中,每次摸出一个球,不放回地依次摸取两次,记为一次抽奖.若摸出的2个球颜色相同则为中奖,否则为不中奖.则下列随机事件的概率正确的是( )
A.某顾客抽奖一次中奖的概率是
B.某顾客抽奖三次,至少有一次中奖的概率是
C.在一次抽奖过程中,若已知顾客第一次抽出了红球,则该顾客中奖的概率是
D.在一次抽奖过程中,若已知顾客第一次抽出了红球,则该顾客中奖的概率是
答案 ABD
解析 顾客抽奖一次中奖的概率为==,故A选项正确;
顾客抽奖三次,至少有一次中奖的概率是1-3=1-3=1-=,故B选项正确;
对于C,D选项,由于第一次抽出了红球,故剩余2个白球和2个红球,再抽一个,抽到红球的概率是=,故C选项错误,D选项正确.
12.已知6的展开式中各项系数的和为2,则下列结论正确的有( )
A.a=1
B.展开式中常数项为160
C.展开式系数的绝对值的和为1 458
D.若r为偶数,则展开式中xr和xr-1的系数相等
答案 ACD
解析 令x=1,可得6的展开式中各项系数的和为(1+a)×1=2,∴a=1,故选项A正确;
∵6=(64x6-192x4+240x2-160+60x-2-12x-4+x-6),故展开式中常数项为-160,故选项B不正确;
6的展开式中各项系数绝对值的和,即6的展开式中各项系数和,
为(1+a)·36=1 458,故选项C正确;
根据6=(64x6-192x4+240x2-160+60x-2-12x-4+x-6)
=64x6-192x4+240x2-160+60x-2-12x-4+x-6+64x5-192x3+240x-+60x-3-12x-5+x-7可得若r为偶数,则展开式中xr和xr-1的系数相等,故选项D正确,故选ACD.
三、填空题(本大题共4小题,每小题5分,共20分)
13.某产品的广告费用x与销售额y的统计数据如下表:
广告费用x(万元) 4 2 3 5
销售额y(万元) 49 26 39 54
根据上表可得线性回归方程y=x+中的为9.4,则=________,据此模型预报广告费用为6万元时销售额为________万元.
答案 9.1 65.5
解析 样本点的中心是(3.5,42),
则=42-9.4×3.5=9.1,
所以线性回归方程是=9.4x+9.1,
把x=6代入得y=65.5.
14.已知平面α的一个法向量为n=(1,-1,0),则y轴与平面α所成的角的大小为________.
答案
解析 y轴的一个方向向量为s=(0,1,0),
cos〈n,s〉==-,
即y轴与平面α所成角的正弦值是,故其所成的角的大小是.
15.5的展开式中常数项是________.
答案 -161
解析 5表示五个相乘,则展开式中的常数项由三种情况产生,
第一种是从五个中分别抽取2x,2x,,,-1,则此时的常数项为C·C·22·(-1)=-120,
第二种情况是从五个中都抽取-1,则此时的常数项为(-1)5=-1,
第三种情况是从五个中分别抽取2x,,-1,-1,-1,
则此时的常数项为C·C·21·(-1)3=-40,
则展开式中常数项为-120-1-40=-161.
16.如图所示,在直平行六面体ABCD-A1B1C1D1中,BD⊥DC,BD=DC=1,点E在AA1上,且AE=AA1=,则点B到平面EDC1的距离为________.
答案
解析 建立如图所示的空间直角坐标系,
则D(0,0,0),A(1,-1,0),B(1,0,0),C(0,1,0),C1(0,1,2),E,
∴=(0,1,2),=.
设平面EDC1的法向量为n=(x,y,z),
则
令z=1,则x=-,y=-2,
∴n=.
∴点B到平面EDC1的距离
d===.
四、解答题(本大题共6小题,共70分)
17.(10分)已知在n的展开式中,________.(填写条件前的序号)
条件①第5项的系数与第3项的系数之比是14∶3;
条件②第2项与倒数第3项的二项式系数之和为55;
条件③C-C=10.
(1)求展开式中二项式系数最大的项;
(2)求展开式中含x5的项.
解 通项公式为
Tr+1=C()n-rr=(-1)rC,
r=0,1,2,…,n.
若填条件①,
(1)依题意得=,即3C=14C,
整理得(n-10)(n+5)=0,
所以n=10或n=-5(舍),
因为n=10,所以10的展开式共有11项,
所以展开式中二项式系数最大的项是第6项,
所以T6=T5+1=(-1)5C
(2)通项公式为Tr+1=(-1)rC,
令=5,得r=0,
所以展开式中含x5的项为x5.
若填条件②,
(1)依题意得C+C=55,
所以n+C=55,
所以n+=55,
即n2+n-110=0,
所以n=10或n=-11(舍),
因为n=10,所以10的展开式共有11项,
所以展开式中二项式系数最大的项是第6项,
所以T6=T5+1=(-1)5C
(2)通项公式为Tr+1=(-1)rC,
令=5,得r=0,
所以展开式中含x5的项为x5.
若填条件③,
(1)依题意得C-C=10,
则C-C=10,
所以-=10,
所以n=10,
因为n=10,所以10的展开式共有11项,
所以展开式中二项式系数最大的项是第6项,
所以T6=T5+1=(-1)5C
(2)通项公式为Tr+1=(-1)rC,
令=5,得r=0,所以展开式中含x5的项为x5.
18.(12分)某医院有2名女医生,3名男医生,3名女护士,1名男护士报名参加某研讨会,医院计划从医生和护士中各选2名参加.
(1)求选出的4名全是女性的方法数;
(2)记X为选出的4名参加者中男性的人数,求X的概率分布和均值.
解 (1)从2名女医生中选2人有C种选法,从3名女护士中选2人有C种选法,则选出的4名全是女性有C·C=3(种)不同的选法.
(2)X的取值可能为0,1,2,3.
P(X=0)==,
P(X=1)==,
P(X=2)==,
P(X=3)==,
列表如下:
X 0 1 2 3
P
∴E(X)=0×+1×+2×+3×=.
19.(12分)在传染病学中,通常把从致病刺激物侵入机体或者对机体发生作用起,到机体出现反应或开始呈现该疾病对应的相关症状的这一阶段称为潜伏期.一研究团队统计了某地区200名患者的相关信息,得到如下表格:
潜伏期(单位:天) [0,2] (2,4] (4,6] (6,8] (8,10] (10,12] (12,14]
人数 17 43 60 50 26 3 1
(1)该传染病的潜伏期受诸多因素的影响,为研究潜伏期与患者年龄的关系,根据上表数据将如下列联表补充完整,并根据列联表判断是否有99%的把握认为该传染病的潜伏期与患者年龄有关.
潜伏期≤6天 潜伏期>6天 合计
50岁以上
(含50岁) 100
50岁以下 55
合计 200
(2)将200名患者的潜伏期超过6天的频率视为该地区每名患者潜伏期超过6天发生的概率,每名患者的潜伏期是否超过6天相互独立.为了深入研究,该团队随机调查了该地区20名患者,其中潜伏期超过6天的人数为X,求随机变量X的均值和方差.
附:
P(χ2≥x0) 0.05 0.025 0.010
x0 3.841 5.024 6.635
解 (1)由题意得列联表:
潜伏期≤6天 潜伏期>6天 合计
50岁以上
(含50岁) 75 25 100
50岁以下 45 55 100
合计 120 80 200
由上表可得
χ2==18.75>6.635,所以有99%的把握认为该传染病的潜伏期与患者年龄有关.
(2)由题意可知,一名患者潜伏期超过6天的概率为
P==,故X~B,
∴E(X)=20×=8,D(X)=20××=.
20.(12分)如图,在三棱锥P-ABC中,PC⊥平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD⊥平面PAB.
(1)求证:AB⊥平面PCB;
(2)求异面直线AP与BC所成角的大小;
(3)求二面角C-PA-B的平面角的余弦值.
(1)证明 ∵PC⊥平面ABC,AB 平面ABC,
∴PC⊥AB.
∵CD⊥平面PAB,AB 平面PAB,
∴CD⊥AB.
又PC∩CD=C,PC,CD 平面PCB,
∴AB⊥平面PCB.
(2)解 由(1)知AB⊥平面PCB,
∴AB⊥BC.
∵PC=AC=2,AB=BC,
∴BC=AB=.
如图,以B为坐标原点,建立空间直角坐标系,则B(0,0,0),A(0,,0),C(,0,0),P(,0,2),
∴=(,-,2),=(,0,0),
则·=×+0+0=2,
∴cos〈,〉===,
故异面直线AP与BC所成的角为.
(3)解 结合(2)中建立的空间直角坐标系,设平面PAB的法向量为m=(x1,y1,z1).
易知=(0,-,0),=(,-,2).
由
得
令z1=-1,得x1=,y1=0,
∴平面PAB的一个法向量为m=(,0,-1).
设平面PAC的法向量为n=(x2,y2,z2).
易知=(0,0,-2),=(,-,0).
由
得令x2=1,得y2=1,z2=0,
∴平面PAC的一个法向量为n=(1,1,0).
∴cos〈m,n〉===.
由图知,二面角C-PA-B的平面角为钝角,
∴二面角C-PA-B的平面角的余弦值为-.
21.(12分)一种室内植物的株高y(单位:cm)与一定范围内的温度x(单位:℃)有关,现收集了该种植物的13组观测数据,得到如图所示的散点图:
现根据散点图利用y=a+b或y=c+建立y关于x的回归方程,令w=,t=,得到如下数据:
10.15 109.94 3.04 0.16
iyi-13 iyi-13 -132 -132 -132
13.94 -2.1 11.67 0.21 21.22
且(wi,yi)与(ti,yi)(i=1,2,3,…,13)的相关系数分别为r1,r2,其中r1=0.885 9.
(1)用相关系数说明哪种模型建立y关于x的回归方程更合适;
(2)①根据(1)的结果及表中数据,求y关于x的回归方程;
②已知这种植物的利润z(单位:千元)与x,y的关系为z=10y-x,当x为何值时,利润的值最大.
附:对于样本(ui,Di)(i=1,2,…,n),其回归直线=u+的斜率和截距的最小二乘法估计公式分别为:
解 (1)由相关系数公式可得
=-≈-≈-0.995 3,
因为|r1|<|r2|<1,
所以用y=c+模型建立y与x的回归方程更合适.
(2)
①
=-=109.94-(-10)×0.16=111.54,
因此,y关于x的回归方程为=111.54-.
②由题意知z=10y-x=10×-x
=1 115.4-,
由基本不等式可得+x≥2=20,
所以z≤1 115.4-20=1 095.4,
当且仅当x=10时等号成立,所以当温度为10 ℃时,这种植物的利润z的值最大.
22.(12分)当今世界环境污染已经成为各国面临的一大难题,其中大气污染是目前城市急需应对的一项课题.某市号召市民尽量减少开车出行以绿色低碳的出行方式支持节能减排.原来天天开车上班的王先生积极响应政府号召,准备每天从骑自行车和开车两种出行方式中随机选择一种方式出行.从即日起出行方式选择规则如下:第一天选择骑自行车方式上班,随后每天用“一次性抛掷4枚均匀硬币”的方法确定出行方式,若得到的正面朝上的枚数小于3,则该天出行方式与前一天相同,否则选择另一种出行方式.
(1)求王先生前三天骑自行车上班的天数X的概率分布;
(2)设Pn(n∈N)表示事件“第n天王先生上班选择的是骑自行车出行方式”的概率.
①用Pn-1表示Pn(n≥2);
②请问王先生的这种选择随机选择出行方式有没有积极响应该市政府的号召?请说明理由.
解 (1)设一次性抛掷4枚均匀的硬币得到正面向上的枚数为ξ,则ξ~B,
P(ξ<3)=C4+C4+C4=,
P(ξ≥3)=1-P(ξ<3)=,
由已知随机变量X的可能取值为1,2,3;
P(X=1)=P(ξ≥3)·P(ξ<3)=×=;
P(X=2)=P(ξ<3)·P(ξ≥3)+P(ξ≥3)·P(ξ≥3)
=×+×=;
P(X=3)=P(ξ<3)·P(ξ<3)=×=.
所以随机变量X的概率分布为
X 1 2 3
P
(2)①设An-1表示事件“第n-1天王先生选择的是骑自行车出行方式”,An表示事件“第n天王先生选择的是骑自行车出行方式”,由全概率公式知
Pn=P(An)=P(An|An-1)P(An-1)+P(An|)P()
=Pn-1·P(ξ<3)+(1-Pn-1)·P(ξ≥3)
=Pn-1+(1-Pn-1)=Pn-1+,
所以Pn=Pn-1+(n≥2).
②由①知Pn-=,n≥2,
又P1=1,所以数列是首项为,公比为的等比数列,所以Pn-=n-1,Pn
=n-1+.
因为Pn=n-1+>恒成立,所以王先生每天选择骑自行车出行方式的概率始终大于选择开车出行方式,从长期来看,王先生选择骑自行车出行方式的次数多于选择开车出行方式的次数是大概率事件,所以王先生积极响应该市政府的号召.
