18.1.2平行四边形的判定(第1课时 ) 课件(共28张PPT)
文档属性
| 名称 | 18.1.2平行四边形的判定(第1课时 ) 课件(共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-20 19:12:19 | ||
图片预览





文档简介
(共28张PPT)
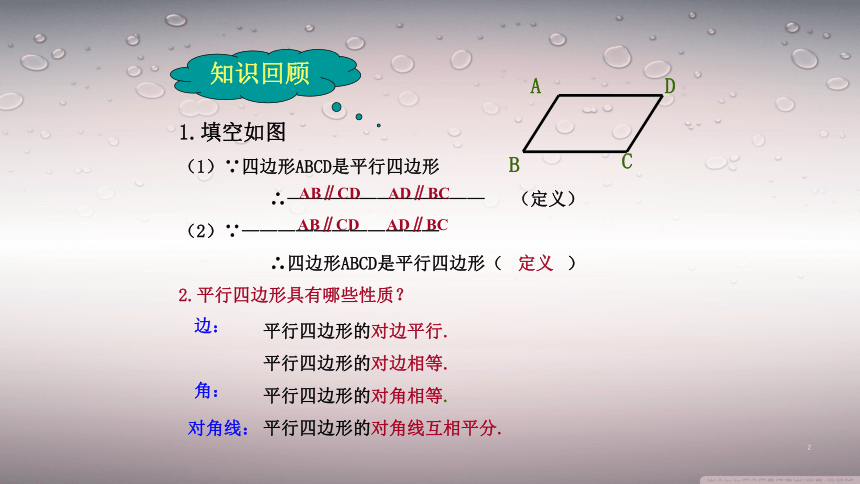
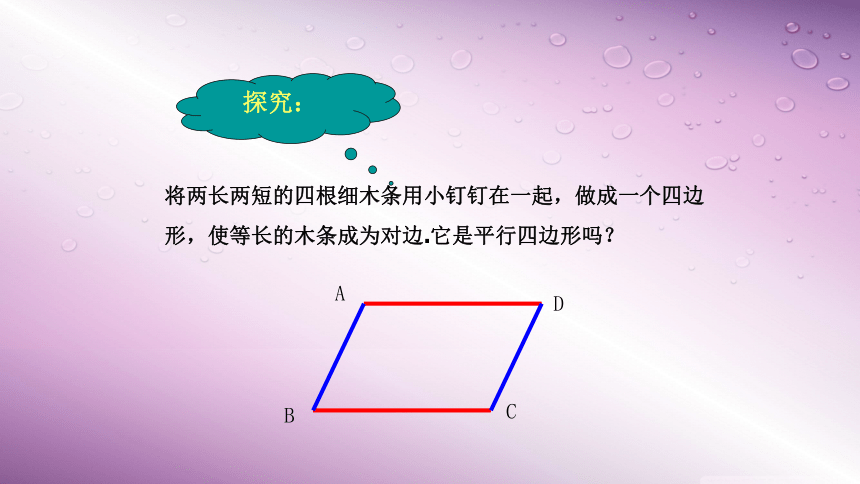
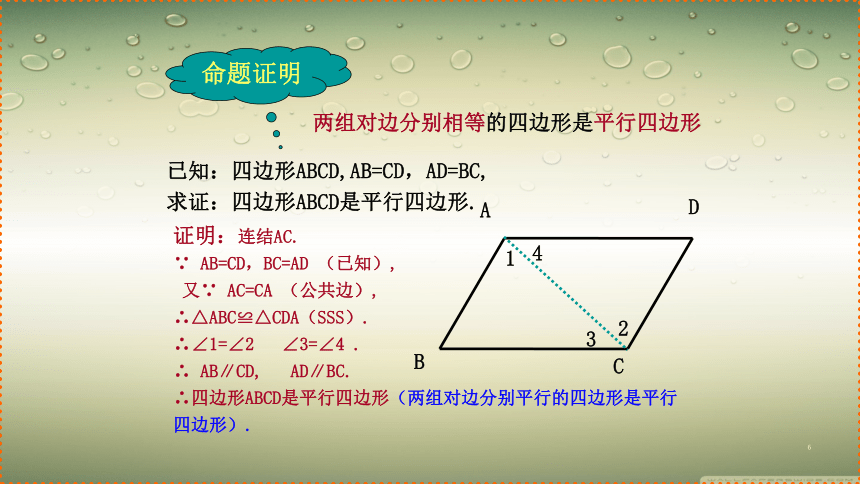
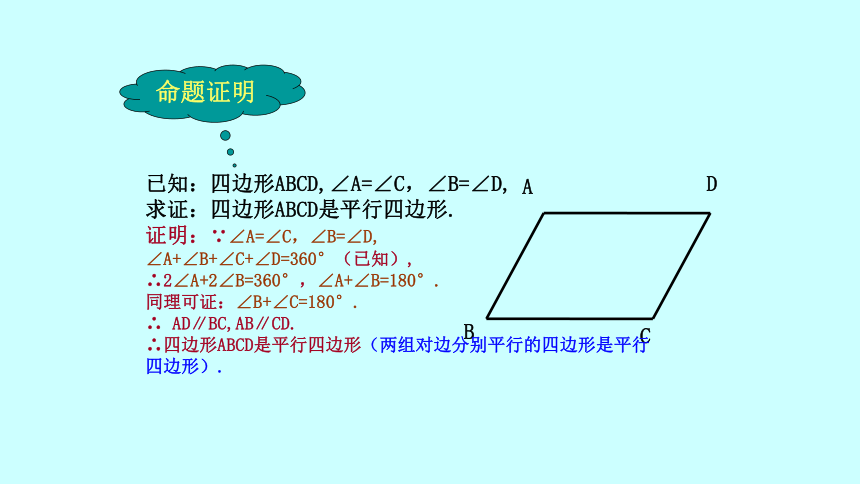
18.1.2平行四边形的判定第1课时 平行四边形的判定2.平行四边形具有哪些性质?知识回顾BCAD1.填空如图(1)∵四边形ABCD是平行四边形∴———————————(定义)(2)∵———————————∴四边形ABCD是平行四边形( )AB∥CD AD∥BCAB∥CD AD∥BC定义平行四边形的对边平行.平行四边形的对边相等.平行四边形的对角相等.平行四边形的对角线互相平分.边:角:对角线:思考:通过前面的学习,我们知道,平行四边形对边相等、对角相等、对角线互相平分.反过来,对边相等或对角相等或对角线互相平分的四边形是不是平行四边形呢?这些逆命题是不是真命题呢?探究:将两长两短的四根细木条用小钉钉在一起,做成一个四边形,使等长的木条成为对边.它是平行四边形吗?ABCD命题1两组对边分别相等的四边形是平行四边形.BCAD两组对边分别相等的四边形是平行四边形已知:四边形ABCD,AB=CD,AD=BC,求证:四边形ABCD是平行四边形.证明:连结AC.∵ AB=CD,BC=AD (已知),又∵ AC=CA (公共边),∴△ABC≌△CDA(SSS).∴∠1=∠2 ∠3=∠4 .∴ AB∥CD, AD∥BC.∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形).2134命题证明判定定理1两组对边分别相等的四边形是平行四边形.BCAD符号语言:∵AB=CD, AD=BC,∴ 四边形ABCD是平行四边形.命题2两组对角分别相等的四边形是平行四边形猜一猜BCAD已知:四边形ABCD,∠A=∠C,∠B=∠D,求证:四边形ABCD是平行四边形.证明:∵∠A=∠C,∠B=∠D,∠A+∠B+∠C+∠D=360°(已知),∴2∠A+2∠B=360°,∠A+∠B=180°.同理可证:∠B+∠C=180°.∴ AD∥BC,AB∥CD.∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形).命题证明判定定理2两组对角分别相等的四边形是平行四边形.符号语言:∵∠A=∠C,∠B=∠D,∴四边形ABCD是平行四边形.BCAD猜一猜命题3对角线互相平分的四边形是平行四边形.将两根细木条的中点重叠,用小钉钉在一起,再用橡皮筋连接木条的顶点做成一个四边形它是平行四边形吗?做一做ABCDO对角线互相平分的四边形是平行四边形.已知:四边形ABCD,对角线AC、BD交于点O,且OA=OC,OB=OD.求证:四边形ABCD是平行四边形.(1)证明:∵OA=OC OD=OB(已知),∠AOB=∠COD(对顶角),∴ △AOB≌△COD(SAS).∴ ∠1 = ∠2.∴AB∥CD.同理 AD∥BC.∴四边形ABCD是平行四边形(2)证明:∵OA=OC OB=OD(已知),∠AOB=∠COD(对顶角),∴ △AOB≌△COD(SAS).∴ AB=CD .同理 AD=CB .∴四边形ABCD是平行四边形.ABCDO12命题证明判定定理3对角线互相平分的四边形是平行四边形.ABCDO符号语言:∵ OA=OC, OB=OD,∴四边形ABCD是平行四边形.试一试判断下列四边形是否是平行四边形 并说明理由.BADC110°110°⑴⑶ABCDO5㎝5㎝4㎝4㎝4.8㎝BADC4.8㎝7.6㎝7.6㎝⑵两组对边分别相等的四边形是平行四边形判定1两组对边分别平行的四边形是平行四边形定义两条对角线互相平分的四边形是平行四边形判定270°探讨规律判定一个四边形是平行四边形应具备几个条件?既可以从位置关系证明,也可以从数量关系证明.判定一个四边形是平行四边形应具备两个条件.已知: ABCD, E、F是AC上的两点,并且AE=CF.求证:四边形BFDE是平行四边形.证明:连接BD交AC于O.∵四边形ABCD是平行四边形,∴ AO=CO,BO=DO.∵AE=CF,∴AO-AE=CO-CF,即 EO=FO.∴ 四边形BFDE是平行四边形.例1:DABCEF昨天初二的李明同学在生物实验室做实验时,不小心碰碎了实验室的一块平行四边形的实验用的玻璃片,只剩下如图所示部分,他想明天星期六回家去割一块赔给学校,带上玻璃剩下部分去玻璃店不安全,于是他想把原来的平行四边形重新在纸上画出来 然后带上图纸去就行了,可原来的平行四边形怎么给它画出来呢?(A,B,C为三顶点,即找出第四个顶点D)ABCDABC根据平行四边形的定义:作AE∥BC,CD∥AB,相交于D点,则四边形ABCD为平行四边形.ADCB一组对边平行且相等的四边形是平行四边形已知:AB∥CD,AB=CD求证:四边形ABCD是平行四边形证明:连接AC.∵AB∥CD,∴∠1=∠2,又AB=CD ,AC=CA,∴△ABC≌△CDA.∴BC=DA.∴四边形ABCD是平行四边形.12命题4平行四边形的第二种判定方法:几何语言表达:∵AD=BC,AD∥BC,∴四边形ABCD为平行四边形(一组对边平行且相等的四边形是平行四边形).ABCD定理4:一组对边平行且相等的四边形是平行四边形例2 已知:如图,E,F分别是平行四边形ABCD的边AD,BC的中点。求证:BE=DF.BFECDA证明:∵四边形ABCD是平行四边形,∴AB∥CD (平行四边形的定义)AB=CD(平行四边形的对边分别相等),∵E,F分别是AD,BC的中点,∴EB=FD,即EB FD.∥﹦∴四边形EBFD是平行四边形(一组对边 平行并且相等的四边形是平行四边形)。平行四边形的第三种判定方法:几何语言表达:∵AB=CD,AD=BC∴四边形ABCD为平行四边形(两组对边分别相等的四边形是平行四边形)ABCD定理2:两组对边分别相等的四边形是平行四边形自学检测:1.在下列条件中,不能判定四边形是平行四边形的是( )AB∥CD,AD∥BCAB=CD,AD=BC(C)AB∥CD,AB=CD(D) AB∥CD,AD=BC(E) AB∥CD, ∠A=∠CDBDAC(两组对边分别平行)(两组对边分别相等)(一组对边平行且相等)(两组对角分别相等)ABDC基础练习:BDAC2.已知:四边形ABCD,∠A=∠C,∠B=∠D.求证:四边形ABCD是平行四边形证明:∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形).同理可证AB∥CD又∵∠A+ ∠B+ ∠C+ ∠D =360 °,∴ 2∠A+ 2∠B=360 °,∵∠A=∠C,∠B=∠D(已知),即∠A+ ∠B=180°.∴ AD∥BC(同旁内角互补,两直线平行)..3.已知:如图,CD是线段AB经平移所得的像,连结AD,BC.求证:四边形ABCD是平行四边形.DCBA证明:∵CD是AB经平移所得的像,∴CD AB,∥﹦∴四边形ABCD是平行四边形(一组对边平行并且相等的四边形是平行四边形).4.直角坐标系内有平行四边形的三个顶点,它们的坐标分别是A(2,1)、B(-1,-2)、C(3 , -2 ),试找出第四个顶点的位置,并写出它的坐标.X轴Y轴-6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6321-1-2-3-4-5-6(-1,-2)BC(3 , -2)(-2,1)DE(6,1)F(0,-5)(2,1)A谢谢!
18.1.2平行四边形的判定第1课时 平行四边形的判定2.平行四边形具有哪些性质?知识回顾BCAD1.填空如图(1)∵四边形ABCD是平行四边形∴———————————(定义)(2)∵———————————∴四边形ABCD是平行四边形( )AB∥CD AD∥BCAB∥CD AD∥BC定义平行四边形的对边平行.平行四边形的对边相等.平行四边形的对角相等.平行四边形的对角线互相平分.边:角:对角线:思考:通过前面的学习,我们知道,平行四边形对边相等、对角相等、对角线互相平分.反过来,对边相等或对角相等或对角线互相平分的四边形是不是平行四边形呢?这些逆命题是不是真命题呢?探究:将两长两短的四根细木条用小钉钉在一起,做成一个四边形,使等长的木条成为对边.它是平行四边形吗?ABCD命题1两组对边分别相等的四边形是平行四边形.BCAD两组对边分别相等的四边形是平行四边形已知:四边形ABCD,AB=CD,AD=BC,求证:四边形ABCD是平行四边形.证明:连结AC.∵ AB=CD,BC=AD (已知),又∵ AC=CA (公共边),∴△ABC≌△CDA(SSS).∴∠1=∠2 ∠3=∠4 .∴ AB∥CD, AD∥BC.∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形).2134命题证明判定定理1两组对边分别相等的四边形是平行四边形.BCAD符号语言:∵AB=CD, AD=BC,∴ 四边形ABCD是平行四边形.命题2两组对角分别相等的四边形是平行四边形猜一猜BCAD已知:四边形ABCD,∠A=∠C,∠B=∠D,求证:四边形ABCD是平行四边形.证明:∵∠A=∠C,∠B=∠D,∠A+∠B+∠C+∠D=360°(已知),∴2∠A+2∠B=360°,∠A+∠B=180°.同理可证:∠B+∠C=180°.∴ AD∥BC,AB∥CD.∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形).命题证明判定定理2两组对角分别相等的四边形是平行四边形.符号语言:∵∠A=∠C,∠B=∠D,∴四边形ABCD是平行四边形.BCAD猜一猜命题3对角线互相平分的四边形是平行四边形.将两根细木条的中点重叠,用小钉钉在一起,再用橡皮筋连接木条的顶点做成一个四边形它是平行四边形吗?做一做ABCDO对角线互相平分的四边形是平行四边形.已知:四边形ABCD,对角线AC、BD交于点O,且OA=OC,OB=OD.求证:四边形ABCD是平行四边形.(1)证明:∵OA=OC OD=OB(已知),∠AOB=∠COD(对顶角),∴ △AOB≌△COD(SAS).∴ ∠1 = ∠2.∴AB∥CD.同理 AD∥BC.∴四边形ABCD是平行四边形(2)证明:∵OA=OC OB=OD(已知),∠AOB=∠COD(对顶角),∴ △AOB≌△COD(SAS).∴ AB=CD .同理 AD=CB .∴四边形ABCD是平行四边形.ABCDO12命题证明判定定理3对角线互相平分的四边形是平行四边形.ABCDO符号语言:∵ OA=OC, OB=OD,∴四边形ABCD是平行四边形.试一试判断下列四边形是否是平行四边形 并说明理由.BADC110°110°⑴⑶ABCDO5㎝5㎝4㎝4㎝4.8㎝BADC4.8㎝7.6㎝7.6㎝⑵两组对边分别相等的四边形是平行四边形判定1两组对边分别平行的四边形是平行四边形定义两条对角线互相平分的四边形是平行四边形判定270°探讨规律判定一个四边形是平行四边形应具备几个条件?既可以从位置关系证明,也可以从数量关系证明.判定一个四边形是平行四边形应具备两个条件.已知: ABCD, E、F是AC上的两点,并且AE=CF.求证:四边形BFDE是平行四边形.证明:连接BD交AC于O.∵四边形ABCD是平行四边形,∴ AO=CO,BO=DO.∵AE=CF,∴AO-AE=CO-CF,即 EO=FO.∴ 四边形BFDE是平行四边形.例1:DABCEF昨天初二的李明同学在生物实验室做实验时,不小心碰碎了实验室的一块平行四边形的实验用的玻璃片,只剩下如图所示部分,他想明天星期六回家去割一块赔给学校,带上玻璃剩下部分去玻璃店不安全,于是他想把原来的平行四边形重新在纸上画出来 然后带上图纸去就行了,可原来的平行四边形怎么给它画出来呢?(A,B,C为三顶点,即找出第四个顶点D)ABCDABC根据平行四边形的定义:作AE∥BC,CD∥AB,相交于D点,则四边形ABCD为平行四边形.ADCB一组对边平行且相等的四边形是平行四边形已知:AB∥CD,AB=CD求证:四边形ABCD是平行四边形证明:连接AC.∵AB∥CD,∴∠1=∠2,又AB=CD ,AC=CA,∴△ABC≌△CDA.∴BC=DA.∴四边形ABCD是平行四边形.12命题4平行四边形的第二种判定方法:几何语言表达:∵AD=BC,AD∥BC,∴四边形ABCD为平行四边形(一组对边平行且相等的四边形是平行四边形).ABCD定理4:一组对边平行且相等的四边形是平行四边形例2 已知:如图,E,F分别是平行四边形ABCD的边AD,BC的中点。求证:BE=DF.BFECDA证明:∵四边形ABCD是平行四边形,∴AB∥CD (平行四边形的定义)AB=CD(平行四边形的对边分别相等),∵E,F分别是AD,BC的中点,∴EB=FD,即EB FD.∥﹦∴四边形EBFD是平行四边形(一组对边 平行并且相等的四边形是平行四边形)。平行四边形的第三种判定方法:几何语言表达:∵AB=CD,AD=BC∴四边形ABCD为平行四边形(两组对边分别相等的四边形是平行四边形)ABCD定理2:两组对边分别相等的四边形是平行四边形自学检测:1.在下列条件中,不能判定四边形是平行四边形的是( )AB∥CD,AD∥BCAB=CD,AD=BC(C)AB∥CD,AB=CD(D) AB∥CD,AD=BC(E) AB∥CD, ∠A=∠CDBDAC(两组对边分别平行)(两组对边分别相等)(一组对边平行且相等)(两组对角分别相等)ABDC基础练习:BDAC2.已知:四边形ABCD,∠A=∠C,∠B=∠D.求证:四边形ABCD是平行四边形证明:∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形).同理可证AB∥CD又∵∠A+ ∠B+ ∠C+ ∠D =360 °,∴ 2∠A+ 2∠B=360 °,∵∠A=∠C,∠B=∠D(已知),即∠A+ ∠B=180°.∴ AD∥BC(同旁内角互补,两直线平行)..3.已知:如图,CD是线段AB经平移所得的像,连结AD,BC.求证:四边形ABCD是平行四边形.DCBA证明:∵CD是AB经平移所得的像,∴CD AB,∥﹦∴四边形ABCD是平行四边形(一组对边平行并且相等的四边形是平行四边形).4.直角坐标系内有平行四边形的三个顶点,它们的坐标分别是A(2,1)、B(-1,-2)、C(3 , -2 ),试找出第四个顶点的位置,并写出它的坐标.X轴Y轴-6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6321-1-2-3-4-5-6(-1,-2)BC(3 , -2)(-2,1)DE(6,1)F(0,-5)(2,1)A谢谢!
