2021-2022学年河北省石家庄市晋州市八年级上学期期末数学试卷(Word版 含解析)
文档属性
| 名称 | 2021-2022学年河北省石家庄市晋州市八年级上学期期末数学试卷(Word版 含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-20 22:23:17 | ||
图片预览




文档简介
2021-2022学年河北省石家庄市晋州市八年级(上)期末数学试卷
注意:本试卷包含Ⅰ、Ⅱ两卷。第Ⅰ卷为选择题,所有答案必须用2B铅笔涂在答题卡中相应的位置。第Ⅱ卷为非选择题,所有答案必须填在答题卷的相应位置。答案写在试卷上均无效,不予记分。
下列选项中,属于最简二次根式的是
A. B. C. D.
下列是医疗或救援的标识,其中既是轴对称图形又是中心对称图形的是
A. B. C. D.
若式子有意义,则的取值可以是
A. B. C. D.
下列条件不能判定两个直角三角形全等的是
A. 两条直角边对应相等 B. 斜边和一锐角对应相等
C. 斜边和一直角边对应相等 D. 两个锐角对应相等
,是两个连续整数,若,则的值为
A. B. C. D.
如图,在中,,,为线段的中点,则的度数是
A.
B.
C.
D.
下列说法中正确的有
是的一个平方根;的平方根和算术平方根都是;的立方根是;近似数精确到百分位;用反证法证明“若,则”时,首先假设“”.
A. 个 B. 个 C. 个 D. 个
如图,在中,,平分,的面积是,则的面积是
A.
B.
C.
D.
下列式子运算结果为的是
A. B. C. D.
如图是嘉嘉的试卷,答对题得分,答错或者不答不得分,则嘉嘉的得分是
A. 分 B. 分 C. 分 D. 分
如图是用三块正方形纸片以顶点相连的方式设计的“毕达哥拉斯”图案.现有五种正方形纸片,面积分别是,,,,,选取其中三块,按图中的方式组成图案,则选取的三块纸片的不可能的是
A. ,,
B. ,,
C. ,,
D. ,,
如图,在中,,,平分,的面积为,则的面积是
A. B. C. D.
定义新运算“”:若,则的值为
A. B. C. D.
如图,≌,与交于点,连接若,,则的度数为
A.
B.
C.
D.
如图所示,在中,,,的垂直平分线交于,交于,下列结论中错误的是
A. 平分
B. 的周长等于
C.
D. 的面积等于的面积
如图,已知线段,于点,,射线于点,点从点向点运动,每秒走,点从点向点运动,每秒走若,同时从出发,则出发秒后,在线段上有一点,使与全等,则的值为
A. B. 或 C. D. 或
命题“三个角都相等的三角形是等边三角形”的逆命题是______;该逆命题是______命题填“真”或“假”.
如图,淇淇在离水面高度为的岸边处,用绳子拉船靠岸,开始时绳子的长为.
开始时,船距岸的距离是______;
若淇淇收绳后,船到达处,则船向岸移动______
如图,是内一点,点,分别在边,上运动.若,,则的周长最小值为______,此时的度数为______.
按要求解答下列各小题.
解方程:;
计算:
老师在黑板上书写了一个代数式的正确计算结果,随后用字母代替了原代数式的一部分.
求代数式,并将其化简;
当时,求的值;
当时,求的值.
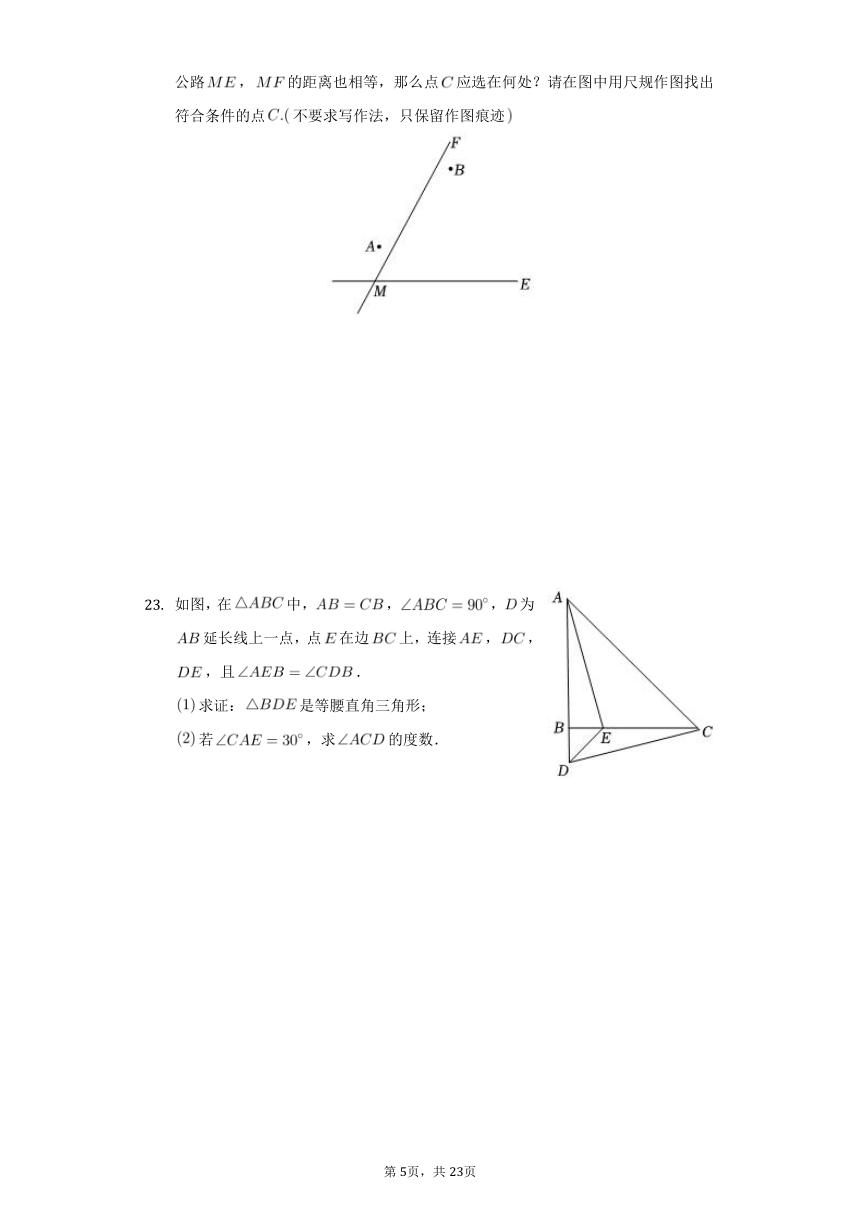
两城镇,与两条公路,的位置如图所示,现电信部门需在的内部处修建一座信号发射塔,要求发射塔到城镇,的距离相等,且到两条公路,的距离也相等,那么点应选在何处?请在图中用尺规作图找出符合条件的点不要求写作法,只保留作图痕迹
如图,在中,,,为延长线上一点,点在边上,连接,,,且.
求证:是等腰直角三角形;
若,求的度数.
为防控新冠肺炎,某药店用元购进若干医用防护口罩,面市后发现供不应求,商店又购进第二批同样的医用防护口罩,所购数量是第一批购进数量的倍,但每只的进价贵了元,结果第二批用了元.
求第一批医用防护口罩每只的进价是多少元?
若药店销售这两批医用防护口罩时,每只的售价都是元,求全部售出后,该药店共盈利多少元?
如图,已知平分,垂直平分,垂足为,点在上,连接交线段于点.
求证:;
若,请你判断与之间的数量关系,并说明理由;
在的条件下,当,时,判断是否为等边三角形?并说明理由.
如图,已知在中,,,,点在上,且,点从点出发沿射线方向以每秒个单位长度的速度向右运动.设点的运动时间为秒,连接.
当秒时,则的长度为______;
当是以为腰的等腰三角形时,求的值;
过点作于点,连接,在点的运动过程中,当平分时,直接写出的值.
答案和解析
1.【答案】
【解析】解:.,不是最简二次根式;
B.,不是最简二次根式;
C.是最简二次根式,符合题意;
D.,不是最简二次根式;
故选:.
利用最简二次根式定义判断即可.
此题考查了最简二次根式,熟练掌握最简二次根式的判定方法是解本题的关键.
2.【答案】
【解析】解:是轴对称图形,不是中心对称图形,故此选项不合题意;
B.不是轴对称图形,也不是中心对称图形,故此选项不合题意;
C.既是轴对称图形又是中心对称图形,故此选项符合题意;
D.不是轴对称图形,也不是中心对称图形,故此选项不合题意.
故选:.
根据轴对称图形与中心对称图形的概念求解.
本题考查了中心对称图形与轴对称图形的概念:轴对称图形的关键是寻找对称轴,图形两部分沿对称轴折叠后可重合;中心对称图形是要寻找对称中心,旋转度后与原图重合.
3.【答案】
【解析】解:由题意可得,
解得:且,
A、,故此选项不符合题意;
B、,故此选项不符合题意;
C、时,原式没有意义,故此选项不符合题意;
D、取时,原式,故此选项符合题意;
故选:.
根据二次根式和分式有意义的条件列不等式组求解.
本题考查二次根式和分式有意义的条件,理解二次根式的有意义的条件被开方数为非负数,分式有意义的条件分母不能为零是解题关键.
4.【答案】
【解析】解:、根据定理可知,两条直角边对应相等的两个三角形全等,本选项不符合题意;
B、根据定理可知,斜边和一锐角对应相等的两个三角形全等,本选项不符合题意;
C、根据定理可知,斜边和一直角边对应相等的两个三角形全等,本选项不符合题意;
D、两个锐角对应相等的两个三角形不一定全等,本选项符合题意;
故选:.
根据三角形全等的判定定理判断即可.
本题考查的是三角形全等的判定,掌握三角形全等的判定定理是解题的关键.
5.【答案】
【解析】解:,
,
,是两个连续整数,若,
,,
,
故选:.
估算出的值即可解答.
本题考查了估算无理数的大小,熟练掌握平方数是解题的关键.
6.【答案】
【解析】解:,为线段的中点,
,
,
,
,
,
故选:.
根据直角三角形斜边上的中线性质求出,根据等腰三角形的性质求出,再求出答案即可.
本题考查了等腰三角形的性质,直角三角形斜边上的中线性质等知识点,能熟记直角三角形斜边上的中线等于斜边的一半是解此题的关键.
7.【答案】
【解析】解:是的一个平方根,说法正确;
的平方根和算术平方根都是,说法正确;
的立方根是,故本说法错误;
近似数精确到个位,故本说法错误;
用反证法证明“若,则”时,首先假设“”,说法正确,
故选:.
根据平方根的概念、立方根的概念、近似数与有效数字以及反证法的一般步骤判断即可.
本题考查的是命题的真假判断,掌握平方根的概念、立方根的概念、近似数与有效数字以及反证法是解题的关键.
8.【答案】
【解析】解:中,,平分,
是三角形的中线,
,
,
.
故选:.
根据等腰三角形的性质得出是三角形的中线,利用三角形的中线得出的面积即可.
此题考查等腰三角形的性质,关键是根据等腰三角形的性质得出是三角形的中线.
9.【答案】
【解析】解:,故选项A的运算结果不是;
,故选项B的运算结果不是;
,故选项C的运算结果是;
,故选项D的运算结果不是;
故选:.
利用分式的运算法则,逐个计算得结论.
本题考查了分式的混合运算,掌握分式的运算法则和运算顺序是解决本题的关键.
10.【答案】
【解析】解:,故此选项不合题意;
,故此选项符合题意;
,故此选项不合题意;
,故此选项符合题意;
答对题得分,答错或者不答不得分,
嘉嘉的得分是:分.
故选:.
直接利用二次根式的性质化简得出答案;
直接利用二次根式的加减运算法则计算得出答案;
直接化简二次根式,再合并得出答案;
直接利用完全平方公式计算得出答案.
此题主要考查了二次根式的加减运算以及二次根式的性质,正确化简二次根式是解题关键.
11.【答案】
【解析】解:由题意可得,
三角形各边的平方是对应的各个正方形的面积,
,故选项A不符合题意;
,故选项B不符合题意;
,故选项C不符合题意;
,故选项D符合题意;
故选:.
根据题意和勾股定理,可以判断各个选项中的条件是否符合题意,从而可以解答本题.
本题考查勾股定理,解答本题的关键是明确题意,利用勾股定理的知识解答.
12.【答案】
【解析】解:中,,,
,
平分,
,
,,
,
:::,,
,
故选:.
利用度角所对的直角边是斜边的一半、三角形的面积计算公式来求两个三角形的面积之比进而求出答案.
本题考查了角平分线的性质、线段垂直平分线的性质.解题时,需要熟悉含角的直角三角形的性质.
13.【答案】
【解析】解:已知等式利用题中的新定义化简得:,
去分母得:,
解得:,
检验:把代入最简公分母得:,
分式方程的解为.
故选:.
已知等式利用题中的新定义化简,求出解即可得到的值.
此题考查了解分式方程,以及有理数的混合运算,弄清题中的新定义是解本题的关键.
14.【答案】
【解析】解:≌,
,
,
,
,
故选:.
根据全等三角形的性质得到,根据三角形外角的性质即可得到结论.
本题考查了全等三角形的性质,三角形外角的性质,熟练掌握全等三角形的性质是解题的关键.
15.【答案】
【解析】解:在中,,,
,
是的垂直平分线,
,
,
,
是的角平分线,故选项A正确;
的周长为,故选项B正确,
在中,,,
,
,
,故选项C正确;
过点作于,
是的角平分线,
,
,
,
在中,,
,
,
,故选项D错误,
故选:.
先求出,再用垂直平分线判断出,进而判断出是的角平分线,判断出选项A正确,再用三角形的周长公式,即可判断出选项B正确,再求出,进而判断出,即可判断出选项C正确,再判断出,再用三角形的面积公式,即可判断出选项D错误.
此题主要考查了等腰三角形的判定和性质,三角形的内角和定理,三角形的周长和面积公式,线段垂直平分线定理,掌握等腰三角形的判定和性质是解本题的关键.
16.【答案】
【解析】解:出发秒,点从点向点运动,每秒走,点从点向点运动,每秒走,
,,则,
,,
,
要使与全等,有两种情况:
,,
即,
解得:;
,,
即,
解得:,
当时,,不符合题意,舍去,
所以,
故选:.
求出,,,根据全等三角形得出,,,,再列出方程,最后求出即可.
本题考查了全等三角形的判定定理,能熟记全等三角形的判定定理是解此题的关键,注意:全等三角形的判定定理有,,,,两直角三角形全等还有等.
17.【答案】等边三角形的三个角都相等 真
【解析】解:“三个角都相等的三角形是等边三角形”的逆命题为“等边三角形的三个角都相等”,逆命题是真命题.
故答案为:等边三角形的三个角都相等;真.
把原命题“三个角都相等的三角形是等边三角形”的题设与结论进行交换即可.
本题考查了命题与定理:判断事物的语句叫命题;正确的命题称为真命题,错误的命题称为假命题;经过推理论证的真命题称为定理.也考查了逆命题.
18.【答案】
【解析】解:在中,,,,
,
故答案为:;
淇淇收绳后,船到达处,
,
,
.
故答案为:
在中,利用勾股定理计算出长;
根据题意可得长,然后再次利用勾股定理计算出长,再利用可得长.
此题主要考查了勾股定理的应用,关键是掌握从题中抽象出勾股定理这一数学模型,画出准确的示意图.领会数形结合的思想的应用.
19.【答案】
【解析】解:分别作点关于、的对称点、,连接,分别交、于点、,连接、、、、.
点关于的对称点为,关于的对称点为,
,,;
点关于的对称点为,
,,,
,,
,
是等边三角形,
.
的周长的最小值.
故答案为:,.
设点关于的对称点为,关于的对称点为,当点、在上时,的周长最小.
本题考查了对称的性质,正确作出图形,理解周长最小的条件是解题的关键.
20.【答案】解:,
,
则,
解得:;
原式
.
【解析】直接利用立方根的定义得出答案;
直接利用二次根式的性质结合二次根式的混合运算法则计算得出答案.
此题主要考查了立方根、二次根式的性质、二次根式混合运算,正确化简各数是解题关键.
21.【答案】解:
;
当时,,
去分母,得:,
解得:,
经检验是原方程的解,
即的值为;
当时,
.
【解析】根据“被除式商除式”,“被减式差减式”列式,然后根据分式乘法和减法运算法则进行计算求解;
根据题意列分式方程求解,注意结果要进行检验;
将已知字母的值代入求值即可.
本题考查分式的化简求值,解分式方程,二次根式的分母有理化计算,理解二次根式的性质,掌握分式混合运算的运算顺序先算乘方,然后算乘除,最后算加减,有小括号先算小括号里面的和计算法则以及解分式方程的步骤是解题关键.
22.【答案】解:如图,点即为所求作的点.
【解析】连接,作线段的垂直平分线,交的角平分线于点,点即为所求.
本题考查作图应用与设计作图,角平分线的性质,线段的垂直平分线等知识,解题的关键是熟练掌握五种基本作图,属于中考常考题型
23.【答案】证明:,
,
在和中,
,
≌,
,
又,
是等腰直角三角形;
解:在中,,,
,
,
,
由得:≌,
,
.
答:的度数为.
【解析】证≌,得,再由,即可得出结论;
由等腰直角三角形的性质得,再,再由全等三角形的性质得,即可得出答案.
本题考查了全等三角形的判定与性质、等腰直角三角形的判定与性质等知识,熟练掌握等腰直角三角形的判定与性质,证明三角形全等是解题的关键.
24.【答案】解:设第一批医用防护口罩每只的进价是元,
依题意,得:,
解得:,
经检验,是所列分式方程的解,且符合题意.
答:第一批医用防护口罩每只的进价是元;
元.
答:该药店共盈利元.
【解析】设第一批医用防护口罩每只的进价是元,则第二批医用防护口罩每只的进价是元,由题意:某药店用元购进若干医用防护口罩,面市后发现供不应求,商店又购进第二批同样的医用防护口罩,所购数量是第一批购进数量的倍,但每只的进价贵了元,结果第二批用了元.列出分式方程,解方程即可;
由每只的售价都是元,结合的结果列式计算即可.
本题考查了分式方程的应用,找准等量关系,正确列出分式方程是解题的关键.
25.【答案】证明:垂直平分,
,
.
又平分,
,
,
;
解:,理由如下:
平分,,
,.
在和中,
,
≌,
.
又,
是的垂直平分线,
,
.
,
.
又,,
;
解:是等边三角形,理由如下:
在和中,
,
≌,
.
,,
.
.
又,
是等边三角形.
【解析】由线段垂直平分线的性质得,则再由角平分线定义得,则,即可得出结论;
证≌,得,再由线段垂直平分线的性质得,则然后由三角形的外角性质即可得出结论;
证≌,得再求出然后由,即可得出结论.
本题考查了全等三角形的判定与性质、线段垂直平分线的性质、平行线的判定、等腰三角形的判定与性质、等边三角形的判定等知识,熟练掌握等腰三角形的判定与性质,证明三角形全等是解题的关键.
26.【答案】
【解析】解:根据题意,得,
,
在中,,
由勾股定理,得,
故答案为:;
在中,,,
由勾股定理,得.
若,则,在中,由勾股定理,得,解得;
若,则 ,解得;
综上所述,当的值为或时,是以为腰的等腰三角形;
点在线段上时,过点作于,如图所示:
则,
,
平分,
,
又,
≌,
,,
,
,
,
在中,由勾股定理得:,
解得:;
点在线段的延长线上时,过点作于,如图所示:
同得:≌,
,,
,
,
,
在中,由勾股定理得:,
解得:;
综上所述,在点的运动过程中,当的值为或时,平分.
根据动点的运动速度和时间先求出,再根据勾股定理即可求解;
分两种情况讨论,由等腰三角形的性质列出等式,即可求解;
分两种情况:点在线段上时,过点作于,先证≌,得出,,再由勾股定理求出,则,然后在中,由勾股定理得出方程,解方程即可;
点在线段的延长线上时,过点作于,同得≌,得出,,再由勾股定理得,则,然后在中,由勾股定理得出方程,解方程即可.
本题是三角形综合题,考查了全等三角形的判定与性质、勾股定理、等腰三角形的性质以及分类讨论等知识;本题综合性强,熟练掌握等腰三角形的性质和勾股定理,证明三角形全等是解本题的关键.
第2页,共2页
第1页,共1页
注意:本试卷包含Ⅰ、Ⅱ两卷。第Ⅰ卷为选择题,所有答案必须用2B铅笔涂在答题卡中相应的位置。第Ⅱ卷为非选择题,所有答案必须填在答题卷的相应位置。答案写在试卷上均无效,不予记分。
下列选项中,属于最简二次根式的是
A. B. C. D.
下列是医疗或救援的标识,其中既是轴对称图形又是中心对称图形的是
A. B. C. D.
若式子有意义,则的取值可以是
A. B. C. D.
下列条件不能判定两个直角三角形全等的是
A. 两条直角边对应相等 B. 斜边和一锐角对应相等
C. 斜边和一直角边对应相等 D. 两个锐角对应相等
,是两个连续整数,若,则的值为
A. B. C. D.
如图,在中,,,为线段的中点,则的度数是
A.
B.
C.
D.
下列说法中正确的有
是的一个平方根;的平方根和算术平方根都是;的立方根是;近似数精确到百分位;用反证法证明“若,则”时,首先假设“”.
A. 个 B. 个 C. 个 D. 个
如图,在中,,平分,的面积是,则的面积是
A.
B.
C.
D.
下列式子运算结果为的是
A. B. C. D.
如图是嘉嘉的试卷,答对题得分,答错或者不答不得分,则嘉嘉的得分是
A. 分 B. 分 C. 分 D. 分
如图是用三块正方形纸片以顶点相连的方式设计的“毕达哥拉斯”图案.现有五种正方形纸片,面积分别是,,,,,选取其中三块,按图中的方式组成图案,则选取的三块纸片的不可能的是
A. ,,
B. ,,
C. ,,
D. ,,
如图,在中,,,平分,的面积为,则的面积是
A. B. C. D.
定义新运算“”:若,则的值为
A. B. C. D.
如图,≌,与交于点,连接若,,则的度数为
A.
B.
C.
D.
如图所示,在中,,,的垂直平分线交于,交于,下列结论中错误的是
A. 平分
B. 的周长等于
C.
D. 的面积等于的面积
如图,已知线段,于点,,射线于点,点从点向点运动,每秒走,点从点向点运动,每秒走若,同时从出发,则出发秒后,在线段上有一点,使与全等,则的值为
A. B. 或 C. D. 或
命题“三个角都相等的三角形是等边三角形”的逆命题是______;该逆命题是______命题填“真”或“假”.
如图,淇淇在离水面高度为的岸边处,用绳子拉船靠岸,开始时绳子的长为.
开始时,船距岸的距离是______;
若淇淇收绳后,船到达处,则船向岸移动______
如图,是内一点,点,分别在边,上运动.若,,则的周长最小值为______,此时的度数为______.
按要求解答下列各小题.
解方程:;
计算:
老师在黑板上书写了一个代数式的正确计算结果,随后用字母代替了原代数式的一部分.
求代数式,并将其化简;
当时,求的值;
当时,求的值.
两城镇,与两条公路,的位置如图所示,现电信部门需在的内部处修建一座信号发射塔,要求发射塔到城镇,的距离相等,且到两条公路,的距离也相等,那么点应选在何处?请在图中用尺规作图找出符合条件的点不要求写作法,只保留作图痕迹
如图,在中,,,为延长线上一点,点在边上,连接,,,且.
求证:是等腰直角三角形;
若,求的度数.
为防控新冠肺炎,某药店用元购进若干医用防护口罩,面市后发现供不应求,商店又购进第二批同样的医用防护口罩,所购数量是第一批购进数量的倍,但每只的进价贵了元,结果第二批用了元.
求第一批医用防护口罩每只的进价是多少元?
若药店销售这两批医用防护口罩时,每只的售价都是元,求全部售出后,该药店共盈利多少元?
如图,已知平分,垂直平分,垂足为,点在上,连接交线段于点.
求证:;
若,请你判断与之间的数量关系,并说明理由;
在的条件下,当,时,判断是否为等边三角形?并说明理由.
如图,已知在中,,,,点在上,且,点从点出发沿射线方向以每秒个单位长度的速度向右运动.设点的运动时间为秒,连接.
当秒时,则的长度为______;
当是以为腰的等腰三角形时,求的值;
过点作于点,连接,在点的运动过程中,当平分时,直接写出的值.
答案和解析
1.【答案】
【解析】解:.,不是最简二次根式;
B.,不是最简二次根式;
C.是最简二次根式,符合题意;
D.,不是最简二次根式;
故选:.
利用最简二次根式定义判断即可.
此题考查了最简二次根式,熟练掌握最简二次根式的判定方法是解本题的关键.
2.【答案】
【解析】解:是轴对称图形,不是中心对称图形,故此选项不合题意;
B.不是轴对称图形,也不是中心对称图形,故此选项不合题意;
C.既是轴对称图形又是中心对称图形,故此选项符合题意;
D.不是轴对称图形,也不是中心对称图形,故此选项不合题意.
故选:.
根据轴对称图形与中心对称图形的概念求解.
本题考查了中心对称图形与轴对称图形的概念:轴对称图形的关键是寻找对称轴,图形两部分沿对称轴折叠后可重合;中心对称图形是要寻找对称中心,旋转度后与原图重合.
3.【答案】
【解析】解:由题意可得,
解得:且,
A、,故此选项不符合题意;
B、,故此选项不符合题意;
C、时,原式没有意义,故此选项不符合题意;
D、取时,原式,故此选项符合题意;
故选:.
根据二次根式和分式有意义的条件列不等式组求解.
本题考查二次根式和分式有意义的条件,理解二次根式的有意义的条件被开方数为非负数,分式有意义的条件分母不能为零是解题关键.
4.【答案】
【解析】解:、根据定理可知,两条直角边对应相等的两个三角形全等,本选项不符合题意;
B、根据定理可知,斜边和一锐角对应相等的两个三角形全等,本选项不符合题意;
C、根据定理可知,斜边和一直角边对应相等的两个三角形全等,本选项不符合题意;
D、两个锐角对应相等的两个三角形不一定全等,本选项符合题意;
故选:.
根据三角形全等的判定定理判断即可.
本题考查的是三角形全等的判定,掌握三角形全等的判定定理是解题的关键.
5.【答案】
【解析】解:,
,
,是两个连续整数,若,
,,
,
故选:.
估算出的值即可解答.
本题考查了估算无理数的大小,熟练掌握平方数是解题的关键.
6.【答案】
【解析】解:,为线段的中点,
,
,
,
,
,
故选:.
根据直角三角形斜边上的中线性质求出,根据等腰三角形的性质求出,再求出答案即可.
本题考查了等腰三角形的性质,直角三角形斜边上的中线性质等知识点,能熟记直角三角形斜边上的中线等于斜边的一半是解此题的关键.
7.【答案】
【解析】解:是的一个平方根,说法正确;
的平方根和算术平方根都是,说法正确;
的立方根是,故本说法错误;
近似数精确到个位,故本说法错误;
用反证法证明“若,则”时,首先假设“”,说法正确,
故选:.
根据平方根的概念、立方根的概念、近似数与有效数字以及反证法的一般步骤判断即可.
本题考查的是命题的真假判断,掌握平方根的概念、立方根的概念、近似数与有效数字以及反证法是解题的关键.
8.【答案】
【解析】解:中,,平分,
是三角形的中线,
,
,
.
故选:.
根据等腰三角形的性质得出是三角形的中线,利用三角形的中线得出的面积即可.
此题考查等腰三角形的性质,关键是根据等腰三角形的性质得出是三角形的中线.
9.【答案】
【解析】解:,故选项A的运算结果不是;
,故选项B的运算结果不是;
,故选项C的运算结果是;
,故选项D的运算结果不是;
故选:.
利用分式的运算法则,逐个计算得结论.
本题考查了分式的混合运算,掌握分式的运算法则和运算顺序是解决本题的关键.
10.【答案】
【解析】解:,故此选项不合题意;
,故此选项符合题意;
,故此选项不合题意;
,故此选项符合题意;
答对题得分,答错或者不答不得分,
嘉嘉的得分是:分.
故选:.
直接利用二次根式的性质化简得出答案;
直接利用二次根式的加减运算法则计算得出答案;
直接化简二次根式,再合并得出答案;
直接利用完全平方公式计算得出答案.
此题主要考查了二次根式的加减运算以及二次根式的性质,正确化简二次根式是解题关键.
11.【答案】
【解析】解:由题意可得,
三角形各边的平方是对应的各个正方形的面积,
,故选项A不符合题意;
,故选项B不符合题意;
,故选项C不符合题意;
,故选项D符合题意;
故选:.
根据题意和勾股定理,可以判断各个选项中的条件是否符合题意,从而可以解答本题.
本题考查勾股定理,解答本题的关键是明确题意,利用勾股定理的知识解答.
12.【答案】
【解析】解:中,,,
,
平分,
,
,,
,
:::,,
,
故选:.
利用度角所对的直角边是斜边的一半、三角形的面积计算公式来求两个三角形的面积之比进而求出答案.
本题考查了角平分线的性质、线段垂直平分线的性质.解题时,需要熟悉含角的直角三角形的性质.
13.【答案】
【解析】解:已知等式利用题中的新定义化简得:,
去分母得:,
解得:,
检验:把代入最简公分母得:,
分式方程的解为.
故选:.
已知等式利用题中的新定义化简,求出解即可得到的值.
此题考查了解分式方程,以及有理数的混合运算,弄清题中的新定义是解本题的关键.
14.【答案】
【解析】解:≌,
,
,
,
,
故选:.
根据全等三角形的性质得到,根据三角形外角的性质即可得到结论.
本题考查了全等三角形的性质,三角形外角的性质,熟练掌握全等三角形的性质是解题的关键.
15.【答案】
【解析】解:在中,,,
,
是的垂直平分线,
,
,
,
是的角平分线,故选项A正确;
的周长为,故选项B正确,
在中,,,
,
,
,故选项C正确;
过点作于,
是的角平分线,
,
,
,
在中,,
,
,
,故选项D错误,
故选:.
先求出,再用垂直平分线判断出,进而判断出是的角平分线,判断出选项A正确,再用三角形的周长公式,即可判断出选项B正确,再求出,进而判断出,即可判断出选项C正确,再判断出,再用三角形的面积公式,即可判断出选项D错误.
此题主要考查了等腰三角形的判定和性质,三角形的内角和定理,三角形的周长和面积公式,线段垂直平分线定理,掌握等腰三角形的判定和性质是解本题的关键.
16.【答案】
【解析】解:出发秒,点从点向点运动,每秒走,点从点向点运动,每秒走,
,,则,
,,
,
要使与全等,有两种情况:
,,
即,
解得:;
,,
即,
解得:,
当时,,不符合题意,舍去,
所以,
故选:.
求出,,,根据全等三角形得出,,,,再列出方程,最后求出即可.
本题考查了全等三角形的判定定理,能熟记全等三角形的判定定理是解此题的关键,注意:全等三角形的判定定理有,,,,两直角三角形全等还有等.
17.【答案】等边三角形的三个角都相等 真
【解析】解:“三个角都相等的三角形是等边三角形”的逆命题为“等边三角形的三个角都相等”,逆命题是真命题.
故答案为:等边三角形的三个角都相等;真.
把原命题“三个角都相等的三角形是等边三角形”的题设与结论进行交换即可.
本题考查了命题与定理:判断事物的语句叫命题;正确的命题称为真命题,错误的命题称为假命题;经过推理论证的真命题称为定理.也考查了逆命题.
18.【答案】
【解析】解:在中,,,,
,
故答案为:;
淇淇收绳后,船到达处,
,
,
.
故答案为:
在中,利用勾股定理计算出长;
根据题意可得长,然后再次利用勾股定理计算出长,再利用可得长.
此题主要考查了勾股定理的应用,关键是掌握从题中抽象出勾股定理这一数学模型,画出准确的示意图.领会数形结合的思想的应用.
19.【答案】
【解析】解:分别作点关于、的对称点、,连接,分别交、于点、,连接、、、、.
点关于的对称点为,关于的对称点为,
,,;
点关于的对称点为,
,,,
,,
,
是等边三角形,
.
的周长的最小值.
故答案为:,.
设点关于的对称点为,关于的对称点为,当点、在上时,的周长最小.
本题考查了对称的性质,正确作出图形,理解周长最小的条件是解题的关键.
20.【答案】解:,
,
则,
解得:;
原式
.
【解析】直接利用立方根的定义得出答案;
直接利用二次根式的性质结合二次根式的混合运算法则计算得出答案.
此题主要考查了立方根、二次根式的性质、二次根式混合运算,正确化简各数是解题关键.
21.【答案】解:
;
当时,,
去分母,得:,
解得:,
经检验是原方程的解,
即的值为;
当时,
.
【解析】根据“被除式商除式”,“被减式差减式”列式,然后根据分式乘法和减法运算法则进行计算求解;
根据题意列分式方程求解,注意结果要进行检验;
将已知字母的值代入求值即可.
本题考查分式的化简求值,解分式方程,二次根式的分母有理化计算,理解二次根式的性质,掌握分式混合运算的运算顺序先算乘方,然后算乘除,最后算加减,有小括号先算小括号里面的和计算法则以及解分式方程的步骤是解题关键.
22.【答案】解:如图,点即为所求作的点.
【解析】连接,作线段的垂直平分线,交的角平分线于点,点即为所求.
本题考查作图应用与设计作图,角平分线的性质,线段的垂直平分线等知识,解题的关键是熟练掌握五种基本作图,属于中考常考题型
23.【答案】证明:,
,
在和中,
,
≌,
,
又,
是等腰直角三角形;
解:在中,,,
,
,
,
由得:≌,
,
.
答:的度数为.
【解析】证≌,得,再由,即可得出结论;
由等腰直角三角形的性质得,再,再由全等三角形的性质得,即可得出答案.
本题考查了全等三角形的判定与性质、等腰直角三角形的判定与性质等知识,熟练掌握等腰直角三角形的判定与性质,证明三角形全等是解题的关键.
24.【答案】解:设第一批医用防护口罩每只的进价是元,
依题意,得:,
解得:,
经检验,是所列分式方程的解,且符合题意.
答:第一批医用防护口罩每只的进价是元;
元.
答:该药店共盈利元.
【解析】设第一批医用防护口罩每只的进价是元,则第二批医用防护口罩每只的进价是元,由题意:某药店用元购进若干医用防护口罩,面市后发现供不应求,商店又购进第二批同样的医用防护口罩,所购数量是第一批购进数量的倍,但每只的进价贵了元,结果第二批用了元.列出分式方程,解方程即可;
由每只的售价都是元,结合的结果列式计算即可.
本题考查了分式方程的应用,找准等量关系,正确列出分式方程是解题的关键.
25.【答案】证明:垂直平分,
,
.
又平分,
,
,
;
解:,理由如下:
平分,,
,.
在和中,
,
≌,
.
又,
是的垂直平分线,
,
.
,
.
又,,
;
解:是等边三角形,理由如下:
在和中,
,
≌,
.
,,
.
.
又,
是等边三角形.
【解析】由线段垂直平分线的性质得,则再由角平分线定义得,则,即可得出结论;
证≌,得,再由线段垂直平分线的性质得,则然后由三角形的外角性质即可得出结论;
证≌,得再求出然后由,即可得出结论.
本题考查了全等三角形的判定与性质、线段垂直平分线的性质、平行线的判定、等腰三角形的判定与性质、等边三角形的判定等知识,熟练掌握等腰三角形的判定与性质,证明三角形全等是解题的关键.
26.【答案】
【解析】解:根据题意,得,
,
在中,,
由勾股定理,得,
故答案为:;
在中,,,
由勾股定理,得.
若,则,在中,由勾股定理,得,解得;
若,则 ,解得;
综上所述,当的值为或时,是以为腰的等腰三角形;
点在线段上时,过点作于,如图所示:
则,
,
平分,
,
又,
≌,
,,
,
,
,
在中,由勾股定理得:,
解得:;
点在线段的延长线上时,过点作于,如图所示:
同得:≌,
,,
,
,
,
在中,由勾股定理得:,
解得:;
综上所述,在点的运动过程中,当的值为或时,平分.
根据动点的运动速度和时间先求出,再根据勾股定理即可求解;
分两种情况讨论,由等腰三角形的性质列出等式,即可求解;
分两种情况:点在线段上时,过点作于,先证≌,得出,,再由勾股定理求出,则,然后在中,由勾股定理得出方程,解方程即可;
点在线段的延长线上时,过点作于,同得≌,得出,,再由勾股定理得,则,然后在中,由勾股定理得出方程,解方程即可.
本题是三角形综合题,考查了全等三角形的判定与性质、勾股定理、等腰三角形的性质以及分类讨论等知识;本题综合性强,熟练掌握等腰三角形的性质和勾股定理,证明三角形全等是解本题的关键.
第2页,共2页
第1页,共1页
同课章节目录
