2021-2022学年高二下学期数学人教A版(2019)选择性必修第三册6.3.2二项式系数的性质与杨辉三角的性质与应用课件(共26张PPT)
文档属性
| 名称 | 2021-2022学年高二下学期数学人教A版(2019)选择性必修第三册6.3.2二项式系数的性质与杨辉三角的性质与应用课件(共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-21 14:44:17 | ||
图片预览







文档简介
(共26张PPT)
第六章 计数原理
6.3.2 二项式系数的性质
杨辉三角的性质与应用
学习目标
1.通过建立“杨辉三角”与二项式系数的关系,归纳二项式系数的性质.
2.学会利用赋值法解决二项式系数和的相关问题.
知识回顾
1.二项式定理(a+b)n=____________________________________________ (n∈N*).
2.二项展开式的通项公式 (a+b)n展开式的通项(展开式的第k+1项),记作Tk+1 =____ __.
3.(a+b)n的展开式各项的二项式系数分别是
4.组合数有哪两个基本性质?
杨辉三角,是二项式系数在三角形中的一种几何排列.在欧洲,这个表叫作帕斯卡三角形.帕斯卡(1623—1662)是在1654年发现这一规律的,比杨辉要迟393年,比贾宪迟600年.杨辉三角是我国古代数学的杰出研究成果之一,它把二项式系数图形化,把组合数内在的一些代数性质直观地从图形中体现出来,是一种离散型的数与形的结合.
问题1:
杨辉三角的上述基本性质
如何用组合数性质解释?
学习新知
新知探究
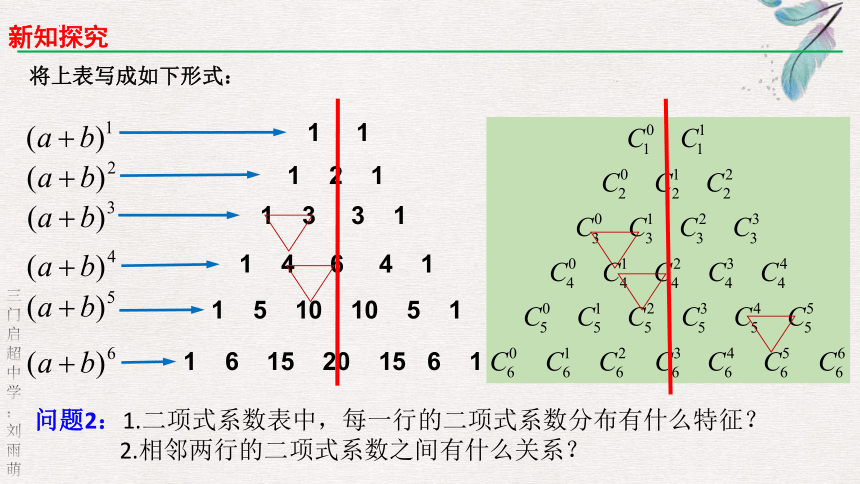
将上表写成如下形式:
1 4 6 4 1
1 1
1 2 1
1 3 3 1
1 5 10 10 5 1
1 6 15 20 15 6 1
问题2:1.二项式系数表中,每一行的二项式系数分布有什么特征?
2.相邻两行的二项式系数之间有什么关系?
新知探究
1 4 6 4 1
1 1
1 2 1
1 3 3 1
1 5 10 10 5 1
1 6 15 20 15 6 1
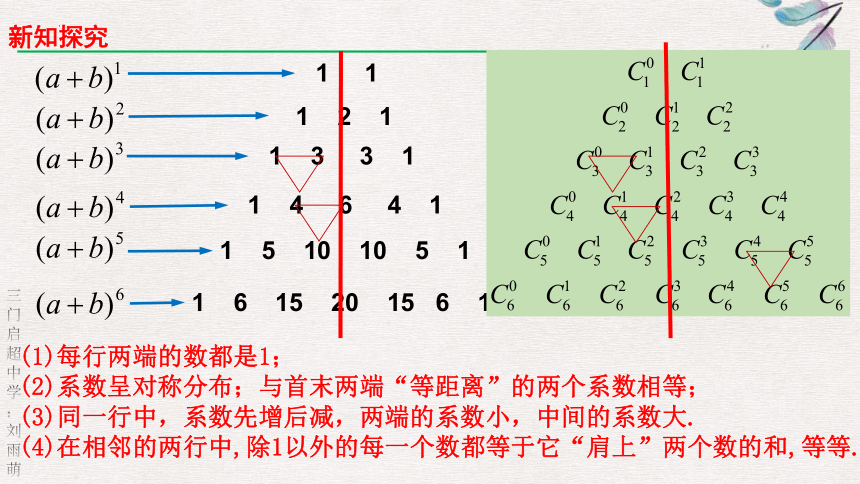
(1)每行两端的数都是1;
(2)系数呈对称分布;与首末两端“等距离”的两个系数相等;
(3)同一行中,系数先增后减,两端的系数小,中间的系数大.
(4)在相邻的两行中,除1以外的每一个数都等于它“肩上”两个数的和,等等.
1 4 6 4 1
1 1
1 2 1
1 3 3 1
1 5 10 10 5 1
1 6 15 20 15 6 1
新知探究
二项式系数的函数解释
问题3:对给定的正整数n,设函数 ,r∈{0,1,2,…,n},
因为 展开式的二项式系数依次是:
从函数角度看, 可看成是以k为自变量的函数 ,其定义域是:
对于确定的n,我们还可以画出它的图象,例如,当n=6时,其图象是右图中的7个孤立点.
追问:一般地,函数 ,r∈{0,1,2,…,n}的图象是什么?
它具有怎样的对称性?
n+1个孤立的点,关于直线 对称
知识概念
二项式系数的函数解释
知识概念
一、二项式系数的性质
典例分析
例1 已知二项式(1-x)8,求:
(1)展开式中二项式系数最大的项;
(2)展开式中系数最小的项.
全品70页例1
巩固练习
1)已知 ,那么 = ;
2) 的展开式中,二项式系数的最大值是 ;
3)若 的展开式中的第十项和第十一项的二项式系数最大,则n= ;
a+b
126
19
课堂小结——你学到了那些新知识呢?
课后作业
课后作业:全品19-20页滚动习题(二)1-15题
二项式系数的性质
学习目标
1.通过小组探究掌握二项式系数和的推导过程.
2.能够区分奇偶项二项式系数和与奇偶次项数和的区别与联系.
3.能用二项式定理解决整除和近似值问题.
新知探究
问题4:
问题5:当x=1时各项系数的和?
二项式系数之和
新知探究
例2:求证在(a+b)n的展开式中,奇数项的二项式系数的和等于偶数项的二项式系数的和.
分析:由(a+b)n的展开式可知,
奇数项的二项式系数的和为
偶数项的二项式系数的和为
由于
因此,我们可以通过对a,b适当赋值来得到上述两个系数和.
证明:
即
即在(a+b)n的展开式中,奇数项的二项式系数的和等于偶数项的二项式系数的和.
新知探究
当a=1,b=1时
各项系数的和
各奇数项二项式系数的和与各偶数项二项式系数的和
例3.在(2x-3y)10的展开式中,求:(1)二项式系数的和;(2)各项系数的和;(3)奇数项的二项式系数和与偶数项的二项式系数和;(4)奇数项系数和与偶数项系数和;
(5)x的奇次项系数和与x的偶次项系数和.
全品20页15题
典例分析
(4)由(2)知,a0+a1+a2+…+a10=1①,
令x=1,y=-1,则(2×1+3×1)10=510=a0-a1+a2-a3+a4-a5+a6-a7+a8-a9+a10②,
由得奇数项的系数和为a0+a2+…+a10= ,由得偶数项的系数和为
例4 (1)[2021·杭州高二期末] 5050被7除的余数为 ( )
A.0 B.1 C.2 D.3
B
(2)1.026的近似值(精确到0.01)为 ( )
A.1.12 B.1.13 C.1.14 D.1.20
B
典例分析
整除和求近似值问题
拓展 (1)求233-1除以9的余数;
(2)求1.025的近似值.(精确到0.01)
巩固练习
课堂小结——你学到了那些新知识呢?
一般地, 展开式的二项式系 有如下性质:
(1)
(对称性)
(2)
(3)当n为偶数时, 最大
当n为奇数时, = 最大
(4)
在(a+b)n的展开式中,奇数项的二项式系数的和等于偶数项的二项式系数的和.
课后作业
课后作业:全品17-18页1-14题必做,15-17选做
第六章 计数原理
6.3.2 二项式系数的性质
杨辉三角的性质与应用
学习目标
1.通过建立“杨辉三角”与二项式系数的关系,归纳二项式系数的性质.
2.学会利用赋值法解决二项式系数和的相关问题.
知识回顾
1.二项式定理(a+b)n=____________________________________________ (n∈N*).
2.二项展开式的通项公式 (a+b)n展开式的通项(展开式的第k+1项),记作Tk+1 =____ __.
3.(a+b)n的展开式各项的二项式系数分别是
4.组合数有哪两个基本性质?
杨辉三角,是二项式系数在三角形中的一种几何排列.在欧洲,这个表叫作帕斯卡三角形.帕斯卡(1623—1662)是在1654年发现这一规律的,比杨辉要迟393年,比贾宪迟600年.杨辉三角是我国古代数学的杰出研究成果之一,它把二项式系数图形化,把组合数内在的一些代数性质直观地从图形中体现出来,是一种离散型的数与形的结合.
问题1:
杨辉三角的上述基本性质
如何用组合数性质解释?
学习新知
新知探究
将上表写成如下形式:
1 4 6 4 1
1 1
1 2 1
1 3 3 1
1 5 10 10 5 1
1 6 15 20 15 6 1
问题2:1.二项式系数表中,每一行的二项式系数分布有什么特征?
2.相邻两行的二项式系数之间有什么关系?
新知探究
1 4 6 4 1
1 1
1 2 1
1 3 3 1
1 5 10 10 5 1
1 6 15 20 15 6 1
(1)每行两端的数都是1;
(2)系数呈对称分布;与首末两端“等距离”的两个系数相等;
(3)同一行中,系数先增后减,两端的系数小,中间的系数大.
(4)在相邻的两行中,除1以外的每一个数都等于它“肩上”两个数的和,等等.
1 4 6 4 1
1 1
1 2 1
1 3 3 1
1 5 10 10 5 1
1 6 15 20 15 6 1
新知探究
二项式系数的函数解释
问题3:对给定的正整数n,设函数 ,r∈{0,1,2,…,n},
因为 展开式的二项式系数依次是:
从函数角度看, 可看成是以k为自变量的函数 ,其定义域是:
对于确定的n,我们还可以画出它的图象,例如,当n=6时,其图象是右图中的7个孤立点.
追问:一般地,函数 ,r∈{0,1,2,…,n}的图象是什么?
它具有怎样的对称性?
n+1个孤立的点,关于直线 对称
知识概念
二项式系数的函数解释
知识概念
一、二项式系数的性质
典例分析
例1 已知二项式(1-x)8,求:
(1)展开式中二项式系数最大的项;
(2)展开式中系数最小的项.
全品70页例1
巩固练习
1)已知 ,那么 = ;
2) 的展开式中,二项式系数的最大值是 ;
3)若 的展开式中的第十项和第十一项的二项式系数最大,则n= ;
a+b
126
19
课堂小结——你学到了那些新知识呢?
课后作业
课后作业:全品19-20页滚动习题(二)1-15题
二项式系数的性质
学习目标
1.通过小组探究掌握二项式系数和的推导过程.
2.能够区分奇偶项二项式系数和与奇偶次项数和的区别与联系.
3.能用二项式定理解决整除和近似值问题.
新知探究
问题4:
问题5:当x=1时各项系数的和?
二项式系数之和
新知探究
例2:求证在(a+b)n的展开式中,奇数项的二项式系数的和等于偶数项的二项式系数的和.
分析:由(a+b)n的展开式可知,
奇数项的二项式系数的和为
偶数项的二项式系数的和为
由于
因此,我们可以通过对a,b适当赋值来得到上述两个系数和.
证明:
即
即在(a+b)n的展开式中,奇数项的二项式系数的和等于偶数项的二项式系数的和.
新知探究
当a=1,b=1时
各项系数的和
各奇数项二项式系数的和与各偶数项二项式系数的和
例3.在(2x-3y)10的展开式中,求:(1)二项式系数的和;(2)各项系数的和;(3)奇数项的二项式系数和与偶数项的二项式系数和;(4)奇数项系数和与偶数项系数和;
(5)x的奇次项系数和与x的偶次项系数和.
全品20页15题
典例分析
(4)由(2)知,a0+a1+a2+…+a10=1①,
令x=1,y=-1,则(2×1+3×1)10=510=a0-a1+a2-a3+a4-a5+a6-a7+a8-a9+a10②,
由得奇数项的系数和为a0+a2+…+a10= ,由得偶数项的系数和为
例4 (1)[2021·杭州高二期末] 5050被7除的余数为 ( )
A.0 B.1 C.2 D.3
B
(2)1.026的近似值(精确到0.01)为 ( )
A.1.12 B.1.13 C.1.14 D.1.20
B
典例分析
整除和求近似值问题
拓展 (1)求233-1除以9的余数;
(2)求1.025的近似值.(精确到0.01)
巩固练习
课堂小结——你学到了那些新知识呢?
一般地, 展开式的二项式系 有如下性质:
(1)
(对称性)
(2)
(3)当n为偶数时, 最大
当n为奇数时, = 最大
(4)
在(a+b)n的展开式中,奇数项的二项式系数的和等于偶数项的二项式系数的和.
课后作业
课后作业:全品17-18页1-14题必做,15-17选做
