18.2.2 菱形的判定(第2课时)课件(共14张PPT)
文档属性
| 名称 | 18.2.2 菱形的判定(第2课时)课件(共14张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 543.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-21 06:20:38 | ||
图片预览




文档简介
(共14张PPT)
八年级 下册
18.2.2 菱形
第2课时 菱形的判定
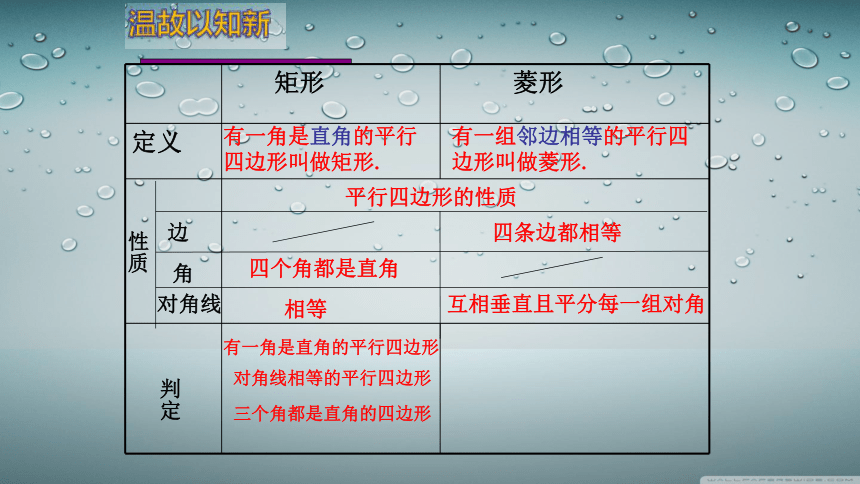
矩形 菱形
定义
有一角是直角的平行四边形叫做矩形.
有一组邻边相等的平行四边形叫做菱形.
平行四边形的性质
性质
边
角
对角线
四个角都是直角
相等
互相垂直且平分每一组对角
判定
有一角是直角的平行四边形
对角线相等的平行四边形
三个角都是直角的四边形
四条边都相等
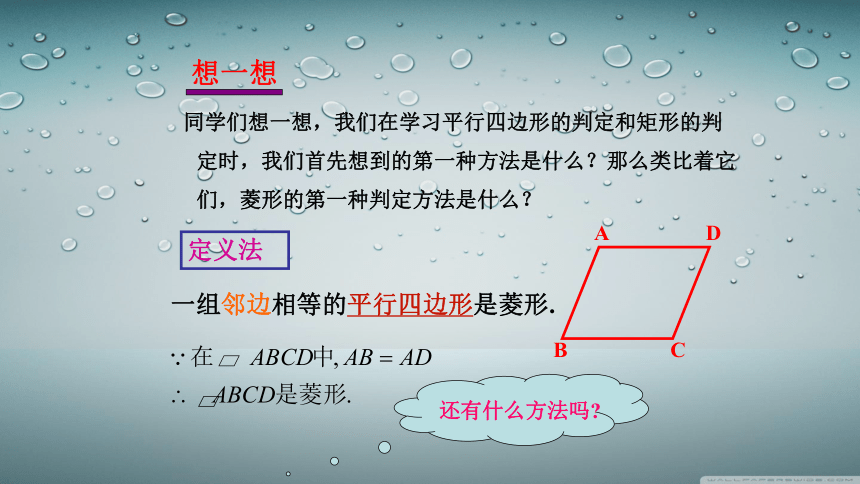
想一想
同学们想一想,我们在学习平行四边形的判定和矩形的判定时,我们首先想到的第一种方法是什么?那么类比着它们,菱形的第一种判定方法是什么?
一组邻边相等的平行四边形是菱形.
定义法
A
B
C
D
还有什么方法吗
探究一
用一长一短两根细木条,在它们的中点处固定一个小钉,做成一个可以转动的十字,四周围上一根橡皮筋,做成一个四边形.转动木条,这个四边形什么时候变成菱形
猜想:
对角线互相垂直的平行四边形是菱形.
对角线互相垂直的平行四边形是菱形.
A
B
C
D
已知:在 中,AC ⊥ BD,
ABCD
ABCD
求证: 是菱形.
证明: ∵四边形ABCD是平行四边形,
∴OA=OC.
又∵ AC ⊥ BD,
∴BA=BC .
∴ ABCD是菱形.
O
定理1:对角线互相垂直的平行四边形是菱形.
例1 如图, ABCD中,对角线AC,BD相交于点O,且
AB=5,AO=4,BO=3.求证: ABCD是菱形.
B
C
A
D
O
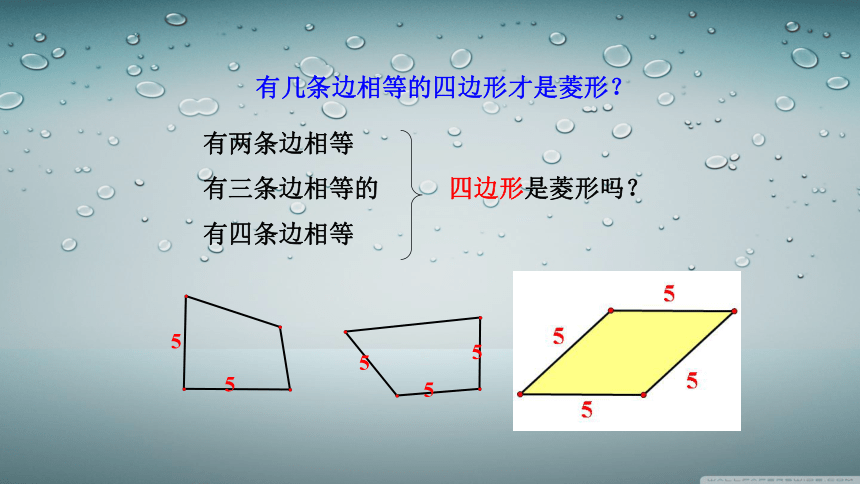
有两条边相等
有三条边相等的 四边形是菱形吗?
有四条边相等
5
5
5
5
5
有几条边相等的四边形才是菱形?
求证:四边都相等的四边形是菱形.
如图,四边形ABCD中,AB=BC=CD=DA.求证:四
边形ABCD是菱形.
D
C
A
B
定理2:四边都相等的四边形是菱形.
发散思维
证明: ∵四边形ABCD中,AB=CD , BC==AD,
∴四边形ABCD是平行四边形.
又∵ AB=BC,
∴ 平行四边形ABCD是菱形.
应用格式:
∵ AB=BC=CD=DA
∴四边形ABCD是菱形.
文字语言 图形语言 符号语言
判定定理1 对角线互相垂直的平行四边形是菱形
判定 定理2 四边相等的四边形是菱形
定义法 一组邻边相等的平行四边形是菱形
菱形的判定
A
B
C
D
∵AB=BC=CD=DA
∴四边形ABCD是菱形
∵□ABCD
AC⊥BD
∴四边形ABCD是菱形
∵□ABCD
AB=AD
∴四边形ABCD是菱形
A
B
C
D
O
A
B
C
D
知识要点
例:在矩形ABCD中,对角线AC的垂直平分线与边AD,BC分别交于点E,F.
求证:四边形AFCE是菱形.
A
B
F
1
2
C
D
O
E
提示
通过证△AOE≌△COF,从而证得EO=OF.
例:在矩形ABCD中,对角线AC的垂直平分线与边AD,BC分别交于点E,F.
求证:四边形AFCE是菱形.
A
B
F
1
2
C
D
O
E
证明:∵四边形ABCD是矩形,
∴AE//FC(矩形的定义)
∴∠1=∠2
又∵∠AOE=∠COF,AO=CO,
∴△AOE≌△COF,
∴EO=FO.
∴四边形是平行四边形(对角线相互平分的四边形是平行四边形).
∴四边形AFCE是菱形(对角线互相垂直的平行四边形是菱形).
1.判断下列说法是否正确?为什么?
(1)对角线互相垂直的四边形是菱形;
(2)对角线互相垂直平分的四边形是菱形;
(3)对角线互相垂直,且有一组邻边相等
的四边形是菱形;
(4)两条邻边相等,且一条对角线平分一
组对角的四边形是菱形.
√
╳
╳
╳
做一做
2. ABCD的对角线AC与BD相交于点O,
(1)若AB=AD,则□ABCD是 形;
(2)若AC=BD,则□ABCD是 形;
(3)若∠ABC是直角,则□ABCD是 形;
(4)若∠BAO=∠DAO,则□ABCD是 形.
A
B
C
D
O
菱
矩
矩
菱
做一做
三个角是直角
四条边都相等
一个角是直角
对角线相等
一组邻边相等
对角线互相垂直
两组对边分别平行
一组对边平行且相等
两组对边分别相等
两组对角分别相等
对角线互相平分
四边形
平行四边形
矩形
菱形
八年级 下册
18.2.2 菱形
第2课时 菱形的判定
矩形 菱形
定义
有一角是直角的平行四边形叫做矩形.
有一组邻边相等的平行四边形叫做菱形.
平行四边形的性质
性质
边
角
对角线
四个角都是直角
相等
互相垂直且平分每一组对角
判定
有一角是直角的平行四边形
对角线相等的平行四边形
三个角都是直角的四边形
四条边都相等
想一想
同学们想一想,我们在学习平行四边形的判定和矩形的判定时,我们首先想到的第一种方法是什么?那么类比着它们,菱形的第一种判定方法是什么?
一组邻边相等的平行四边形是菱形.
定义法
A
B
C
D
还有什么方法吗
探究一
用一长一短两根细木条,在它们的中点处固定一个小钉,做成一个可以转动的十字,四周围上一根橡皮筋,做成一个四边形.转动木条,这个四边形什么时候变成菱形
猜想:
对角线互相垂直的平行四边形是菱形.
对角线互相垂直的平行四边形是菱形.
A
B
C
D
已知:在 中,AC ⊥ BD,
ABCD
ABCD
求证: 是菱形.
证明: ∵四边形ABCD是平行四边形,
∴OA=OC.
又∵ AC ⊥ BD,
∴BA=BC .
∴ ABCD是菱形.
O
定理1:对角线互相垂直的平行四边形是菱形.
例1 如图, ABCD中,对角线AC,BD相交于点O,且
AB=5,AO=4,BO=3.求证: ABCD是菱形.
B
C
A
D
O
有两条边相等
有三条边相等的 四边形是菱形吗?
有四条边相等
5
5
5
5
5
有几条边相等的四边形才是菱形?
求证:四边都相等的四边形是菱形.
如图,四边形ABCD中,AB=BC=CD=DA.求证:四
边形ABCD是菱形.
D
C
A
B
定理2:四边都相等的四边形是菱形.
发散思维
证明: ∵四边形ABCD中,AB=CD , BC==AD,
∴四边形ABCD是平行四边形.
又∵ AB=BC,
∴ 平行四边形ABCD是菱形.
应用格式:
∵ AB=BC=CD=DA
∴四边形ABCD是菱形.
文字语言 图形语言 符号语言
判定定理1 对角线互相垂直的平行四边形是菱形
判定 定理2 四边相等的四边形是菱形
定义法 一组邻边相等的平行四边形是菱形
菱形的判定
A
B
C
D
∵AB=BC=CD=DA
∴四边形ABCD是菱形
∵□ABCD
AC⊥BD
∴四边形ABCD是菱形
∵□ABCD
AB=AD
∴四边形ABCD是菱形
A
B
C
D
O
A
B
C
D
知识要点
例:在矩形ABCD中,对角线AC的垂直平分线与边AD,BC分别交于点E,F.
求证:四边形AFCE是菱形.
A
B
F
1
2
C
D
O
E
提示
通过证△AOE≌△COF,从而证得EO=OF.
例:在矩形ABCD中,对角线AC的垂直平分线与边AD,BC分别交于点E,F.
求证:四边形AFCE是菱形.
A
B
F
1
2
C
D
O
E
证明:∵四边形ABCD是矩形,
∴AE//FC(矩形的定义)
∴∠1=∠2
又∵∠AOE=∠COF,AO=CO,
∴△AOE≌△COF,
∴EO=FO.
∴四边形是平行四边形(对角线相互平分的四边形是平行四边形).
∴四边形AFCE是菱形(对角线互相垂直的平行四边形是菱形).
1.判断下列说法是否正确?为什么?
(1)对角线互相垂直的四边形是菱形;
(2)对角线互相垂直平分的四边形是菱形;
(3)对角线互相垂直,且有一组邻边相等
的四边形是菱形;
(4)两条邻边相等,且一条对角线平分一
组对角的四边形是菱形.
√
╳
╳
╳
做一做
2. ABCD的对角线AC与BD相交于点O,
(1)若AB=AD,则□ABCD是 形;
(2)若AC=BD,则□ABCD是 形;
(3)若∠ABC是直角,则□ABCD是 形;
(4)若∠BAO=∠DAO,则□ABCD是 形.
A
B
C
D
O
菱
矩
矩
菱
做一做
三个角是直角
四条边都相等
一个角是直角
对角线相等
一组邻边相等
对角线互相垂直
两组对边分别平行
一组对边平行且相等
两组对边分别相等
两组对角分别相等
对角线互相平分
四边形
平行四边形
矩形
菱形
