人教版八下数学第十七章 17.2勾股定理的逆定理同步练习 (word版含答案)
文档属性
| 名称 | 人教版八下数学第十七章 17.2勾股定理的逆定理同步练习 (word版含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 160.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-21 00:00:00 | ||
图片预览



文档简介
勾股定理的逆定理同步练习
一、选择题
1.长度为下列四组数据的线段中,可以构成直角三角形的是( )
A.1,2,3 B.2,3,4 C.3,4,5 D.4,5,6
2.将直角三角形的各边都缩小或扩大同样的倍数后,得到的三角形是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.不确定
3.如图,以 的三边为直角边分别向外作等腰直角三角形.若 ,则图中阴影部分的面积为( )
A.3 B. C. D.
4.如图,在4×4的正方形网格中,每个小正方形的边长均为1,点A,B,C都在格点上,AD⊥BC于点D,则AD的长为( )
A. B.2 C. D.3
5.如图,五根小木棒,其长度分别为5,9,12,13,15,现将它们摆成两个直角三角形,其中正确的是( )
A. B.
C. D.
6.如图所示,有一个高18cm,底面周长为24cm的圆柱形玻璃容器,在外侧距下底1cm的点S处有一蜘蛛,与蜘蛛相对的圆柱形容器的上口外侧距开口处1cm的点F处有一只苍蝇,则急于捕获苍蝇充饥的蜘蛛所走的最短路径的长度是( )
A.16cm B.18cm C.20cm D.24cm
7.下列结论中,错误的有( )
①Rt△ABC中,已知两边分别为3和4,则第三边的长为5;
②三角形的三边分别为a、b、c,若a2+b2=c2,则∠A=90°;
③若△ABC中,∠A:∠B:∠C=1:5:6,则这个三角形是一个直角三角形;
④若(x﹣y)2+M=(x+y)2成立,则M=4xy.
A.0个 B.1个 C.2个 D.3个
8.如图,在正方形ABCD中,点P在对角线BD上,PE⊥BC,PF⊥CD,E,F分别为垂足,连结AP,EF,则下列命题:①若AP=5,则EF=5;②若AP⊥BD,则EF∥BD;③若正方形边长为4,则EF的最小值为2,其中正确的命题是( )
A.①② B.①③ C.②③ D.①②③
二、填空题
9.如图,已知阴影部分是一个正方形, ,则此正方形的面积为
10.如图,一棵大树在一次强台风中于离地面 处折断倒下,树干顶部在距离根部 处,这棵大树在折断前的高度为 .
11.如图,长方体的长为15厘米,宽为10厘米,高为20厘米,点B到点C的距离是5厘米。一只小虫在长方体表面从A爬到B的最短路程是
12.有两棵树,一棵高5米,另一棵高2米,两棵树的距离有4米,一只小鸟从一棵树的树顶端飞到另一棵树的顶端,那么请问:这只小鸟至少要飞了 米.
13.如图,每个小正方形的边长为1, 的各点都在网格的格点上,点 为 的中点,则线段 的长 .
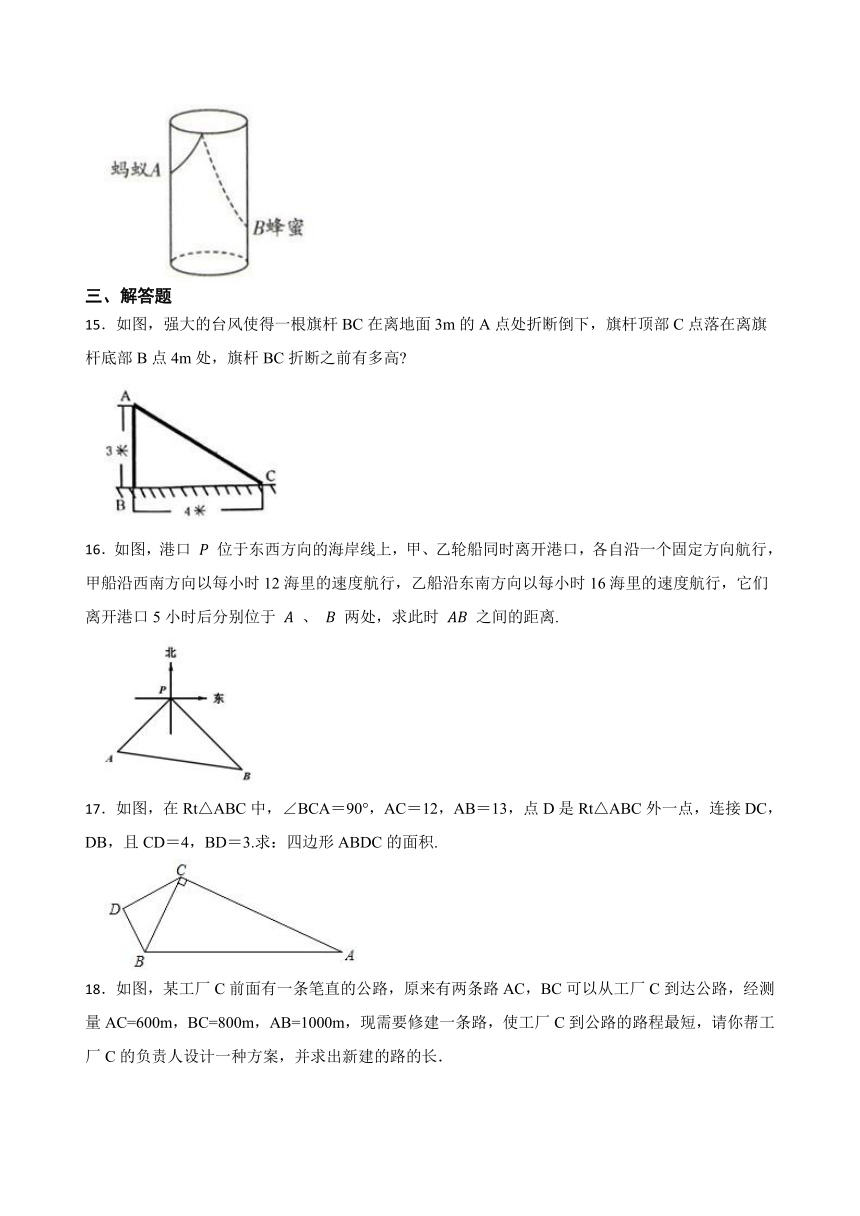
14.如图所示,圆柱形玻璃杯高为14cm,底面周长为32cm,在杯内壁离杯底5cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿3 cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到内壁B处的最短距离为 cm. (杯壁厚度不计)
三、解答题
15.如图,强大的台风使得一根旗杆BC在离地面3m的A点处折断倒下,旗杆顶部C点落在离旗杆底部B点4m处,旗杆BC折断之前有多高
16.如图,港口 位于东西方向的海岸线上,甲、乙轮船同时离开港口,各自沿一个固定方向航行,甲船沿西南方向以每小时12海里的速度航行,乙船沿东南方向以每小时16海里的速度航行,它们离开港口5小时后分别位于 、 两处,求此时 之间的距离.
17.如图,在Rt△ABC中,∠BCA=90°,AC=12,AB=13,点D是Rt△ABC外一点,连接DC,DB,且CD=4,BD=3.求:四边形ABDC的面积.
18.如图,某工厂C前面有一条笔直的公路,原来有两条路AC,BC可以从工厂C到达公路,经测量AC=600m,BC=800m,AB=1000m,现需要修建一条路,使工厂C到公路的路程最短,请你帮工厂C的负责人设计一种方案,并求出新建的路的长.
19.如图,在四边形ABCD中,AD=4,BC=1,∠A=30°,∠B=90°,∠ADC=120°,求CD的长.
20.如图第4号台风“黑格比”的中心于2020年8月5日下午位于浙江省绍兴市境内的B处,最大风力有9级(23m/s),中心最低气压为990百帕,台风中心沿东北(BC)方向以25km/h的速度向D移动在距离B地250km的正北方有一A地,已知A地到BC的距离AD=70km,那么台风中心经过多长时间从B点移到D点?如果在距台风中心70km的圆形区域内都将有受到台风破坏的危险,正在D点休闲的游人在接到台风警报后的几个小时内撤离才可脱离危险?
答案解析部分
1.【答案】C
2.【答案】B
3.【答案】A
4.【答案】B
5.【答案】C
6.【答案】C
7.【答案】C
8.【答案】A
9.【答案】8
10.【答案】8
11.【答案】25厘米
12.【答案】5
13.【答案】
14.【答案】20
15.【答案】解:在Rt△ABC中,AB=3,BC=4 AC2=AB2+BC2=52,解得AC=5
∴BC=AB+AC=3+5=8
所以旗杆折断之前高度为8m。
16.【答案】解:如图,由已知得,AP=12×5=60海里,PB=16×5=80海里,
在△APB中
∵∠APB=90°,
由勾股定理得AP2+PB2=AB2,
即602+802=AB2,
AB= =100海里.
答:此时A、B之间的距离相距100海里.
17.【答案】解:∵Rt△ABC中,∠BCA=90°,AC=12,AB=13,
∴BC= = =5;
∵在△BCD中,CD=4,BD=3,BC=5,
∴CD2+BD2=BC2,
∴△BCD是直角三角形,
∴四边形ABDC的面积=S△ABC+S△BCD= ×12×5+ ×3×4=36.
18.【答案】解:过点C作公路AB的垂线,垂足为D,则线段CD即为新建的路.
∵AC2+BC2 =6002 +8002=1 0002 ,AB2=1 0002,
∴AC2 +BC2=AB2,.∴△ABC为直角三角形.
由三角形的面积公式知 AB·CD= AC·BC,
×1 000·CD= ×600×800,
∴CD= 480 m,即新建的路的长为480 m.
19.【答案】解:延长AD、BC,两条延长线交于点E,
∵∠B=90°,∠A=30°
∴∠E=60°
∵∠ADC=120°
∴∠CDE=60°
∴△CDE是等边三角形
则CD=CE=DE
设CD=x,则CE=DE=x,AE=x+4,BE=x+1
∵ 在Rt△ABE中,∠A=30°
∴ x+4=2(x+1)
解得:x=2
∴CD=2.
20.【答案】解:在 ΔABD中,根据勾股定理,BD= = =240(km),
则台风中心经过240÷25= 小时从B点移到D点,
如图,距台风中心70km的圆形区域内都会受到不同程度的影响,
∴所以人们要在台风中心到达E点之前撤离,
∵BE=BD-DE=240-70=170km,170÷25= (小时),
∴正在D点休闲的游人在接到台风警报后的 小时内撤离才可脱离危险.
一、选择题
1.长度为下列四组数据的线段中,可以构成直角三角形的是( )
A.1,2,3 B.2,3,4 C.3,4,5 D.4,5,6
2.将直角三角形的各边都缩小或扩大同样的倍数后,得到的三角形是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.不确定
3.如图,以 的三边为直角边分别向外作等腰直角三角形.若 ,则图中阴影部分的面积为( )
A.3 B. C. D.
4.如图,在4×4的正方形网格中,每个小正方形的边长均为1,点A,B,C都在格点上,AD⊥BC于点D,则AD的长为( )
A. B.2 C. D.3
5.如图,五根小木棒,其长度分别为5,9,12,13,15,现将它们摆成两个直角三角形,其中正确的是( )
A. B.
C. D.
6.如图所示,有一个高18cm,底面周长为24cm的圆柱形玻璃容器,在外侧距下底1cm的点S处有一蜘蛛,与蜘蛛相对的圆柱形容器的上口外侧距开口处1cm的点F处有一只苍蝇,则急于捕获苍蝇充饥的蜘蛛所走的最短路径的长度是( )
A.16cm B.18cm C.20cm D.24cm
7.下列结论中,错误的有( )
①Rt△ABC中,已知两边分别为3和4,则第三边的长为5;
②三角形的三边分别为a、b、c,若a2+b2=c2,则∠A=90°;
③若△ABC中,∠A:∠B:∠C=1:5:6,则这个三角形是一个直角三角形;
④若(x﹣y)2+M=(x+y)2成立,则M=4xy.
A.0个 B.1个 C.2个 D.3个
8.如图,在正方形ABCD中,点P在对角线BD上,PE⊥BC,PF⊥CD,E,F分别为垂足,连结AP,EF,则下列命题:①若AP=5,则EF=5;②若AP⊥BD,则EF∥BD;③若正方形边长为4,则EF的最小值为2,其中正确的命题是( )
A.①② B.①③ C.②③ D.①②③
二、填空题
9.如图,已知阴影部分是一个正方形, ,则此正方形的面积为
10.如图,一棵大树在一次强台风中于离地面 处折断倒下,树干顶部在距离根部 处,这棵大树在折断前的高度为 .
11.如图,长方体的长为15厘米,宽为10厘米,高为20厘米,点B到点C的距离是5厘米。一只小虫在长方体表面从A爬到B的最短路程是
12.有两棵树,一棵高5米,另一棵高2米,两棵树的距离有4米,一只小鸟从一棵树的树顶端飞到另一棵树的顶端,那么请问:这只小鸟至少要飞了 米.
13.如图,每个小正方形的边长为1, 的各点都在网格的格点上,点 为 的中点,则线段 的长 .
14.如图所示,圆柱形玻璃杯高为14cm,底面周长为32cm,在杯内壁离杯底5cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿3 cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到内壁B处的最短距离为 cm. (杯壁厚度不计)
三、解答题
15.如图,强大的台风使得一根旗杆BC在离地面3m的A点处折断倒下,旗杆顶部C点落在离旗杆底部B点4m处,旗杆BC折断之前有多高
16.如图,港口 位于东西方向的海岸线上,甲、乙轮船同时离开港口,各自沿一个固定方向航行,甲船沿西南方向以每小时12海里的速度航行,乙船沿东南方向以每小时16海里的速度航行,它们离开港口5小时后分别位于 、 两处,求此时 之间的距离.
17.如图,在Rt△ABC中,∠BCA=90°,AC=12,AB=13,点D是Rt△ABC外一点,连接DC,DB,且CD=4,BD=3.求:四边形ABDC的面积.
18.如图,某工厂C前面有一条笔直的公路,原来有两条路AC,BC可以从工厂C到达公路,经测量AC=600m,BC=800m,AB=1000m,现需要修建一条路,使工厂C到公路的路程最短,请你帮工厂C的负责人设计一种方案,并求出新建的路的长.
19.如图,在四边形ABCD中,AD=4,BC=1,∠A=30°,∠B=90°,∠ADC=120°,求CD的长.
20.如图第4号台风“黑格比”的中心于2020年8月5日下午位于浙江省绍兴市境内的B处,最大风力有9级(23m/s),中心最低气压为990百帕,台风中心沿东北(BC)方向以25km/h的速度向D移动在距离B地250km的正北方有一A地,已知A地到BC的距离AD=70km,那么台风中心经过多长时间从B点移到D点?如果在距台风中心70km的圆形区域内都将有受到台风破坏的危险,正在D点休闲的游人在接到台风警报后的几个小时内撤离才可脱离危险?
答案解析部分
1.【答案】C
2.【答案】B
3.【答案】A
4.【答案】B
5.【答案】C
6.【答案】C
7.【答案】C
8.【答案】A
9.【答案】8
10.【答案】8
11.【答案】25厘米
12.【答案】5
13.【答案】
14.【答案】20
15.【答案】解:在Rt△ABC中,AB=3,BC=4 AC2=AB2+BC2=52,解得AC=5
∴BC=AB+AC=3+5=8
所以旗杆折断之前高度为8m。
16.【答案】解:如图,由已知得,AP=12×5=60海里,PB=16×5=80海里,
在△APB中
∵∠APB=90°,
由勾股定理得AP2+PB2=AB2,
即602+802=AB2,
AB= =100海里.
答:此时A、B之间的距离相距100海里.
17.【答案】解:∵Rt△ABC中,∠BCA=90°,AC=12,AB=13,
∴BC= = =5;
∵在△BCD中,CD=4,BD=3,BC=5,
∴CD2+BD2=BC2,
∴△BCD是直角三角形,
∴四边形ABDC的面积=S△ABC+S△BCD= ×12×5+ ×3×4=36.
18.【答案】解:过点C作公路AB的垂线,垂足为D,则线段CD即为新建的路.
∵AC2+BC2 =6002 +8002=1 0002 ,AB2=1 0002,
∴AC2 +BC2=AB2,.∴△ABC为直角三角形.
由三角形的面积公式知 AB·CD= AC·BC,
×1 000·CD= ×600×800,
∴CD= 480 m,即新建的路的长为480 m.
19.【答案】解:延长AD、BC,两条延长线交于点E,
∵∠B=90°,∠A=30°
∴∠E=60°
∵∠ADC=120°
∴∠CDE=60°
∴△CDE是等边三角形
则CD=CE=DE
设CD=x,则CE=DE=x,AE=x+4,BE=x+1
∵ 在Rt△ABE中,∠A=30°
∴ x+4=2(x+1)
解得:x=2
∴CD=2.
20.【答案】解:在 ΔABD中,根据勾股定理,BD= = =240(km),
则台风中心经过240÷25= 小时从B点移到D点,
如图,距台风中心70km的圆形区域内都会受到不同程度的影响,
∴所以人们要在台风中心到达E点之前撤离,
∵BE=BD-DE=240-70=170km,170÷25= (小时),
∴正在D点休闲的游人在接到台风警报后的 小时内撤离才可脱离危险.
