2021-2022学年苏科版八年级数学下册9.3平行四边形知识点分类训练(Word版含答案)
文档属性
| 名称 | 2021-2022学年苏科版八年级数学下册9.3平行四边形知识点分类训练(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 247.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-21 00:00:00 | ||
图片预览




文档简介
2021-2022学年苏科版八年级数学下册《9-3平行四边形》知识点分类训练(附答案)
一.平行四边形的性质
1.如图,在 ABCD中,AC=11,BC=7,BD⊥AB,则AB= .
2.在平面直角坐标系xOy中,已知四边形ABCD是平行四边形,且点A(0,﹣2),点B(m,m+1),点C(6,2).
(1)线段AC的中点E的坐标为 ;
(2)对角线BD长的最小值为 .
3.在平行四边形ABCD中,BC边上的高为AE=4,AB=5,EC=7,则平行四边形ABCD的周长等于 .
4.如图,在平行四边形ABCD中,∠B<90°,BC>AB,点E、F分别在边BC和CD上,AE=6,AF=8,∠EAF=60°.
(1)若AE⊥BC,AF⊥CD,则CD:BC= ;
(2)若点E、F在分别是边BC和CD的中点,则AD= .
5.在平行四边形ABCD中,∠A=45°,BC=2,则AB与CD之间的距离为 .
6.如图所示,在 ABCD中,点E在线段BC上且BE=2CE,点F是CD边的中点,若AE=4,AF=4,且∠EAF=45°,则AB的长是 .
7.如图,在 ABCD中,AE⊥BC于E,AF⊥CD于F,∠EAF=45°,且AE+AF=5,则平行四边形ABCD的周长为 .
8.如图,过平行四边形ABCD的对角找BD上一点M分别作平行四边形两边的平行线EF与GH,那么图中的平行四边形AEMG的面积S1与平行四边形HCFM的面积S2的大小关系是 .
二.平行四边形的判定
9.如图,点E,F是 ABCD对角线上两点,在条件:①DE=BF;②∠ADE=∠CBF;③AF=CE;④∠AEB=∠CFD中,选择一个条件添加,使四边形DEBF是平行四边形可添加的条件有 (写出所有正确条件的序号)
10.若以A(﹣0.5,0),B(2,0),C(0,1)三点为顶点要画平行四边形,则第四个顶点不可能在第 象限.
11.在平面直角坐标系xOy中,有A(3,2),B(﹣1,﹣4),P是x轴上的一点,Q是y轴上的一点,若以点A,B,P,Q四个点为顶点的四边形是平行四边形,则Q点的坐标是 .
三.平行四边形的判定与性质
12.如图,在 ABCD中,AC,BD相交于点O,点E,F在对角线BD上,有下列条件:①BF=DE;②AE=CF;③∠EAB=∠FCD;④AF∥CE.其中一定能判定四边形AECF是平行四边形的是 .
13.四边形ABCD中,若∠DAC=∠BCA,∠DCA=∠BAC,且∠D=52°,则∠B= .
14.如图,平行四边形ABCD中,AB=8cm,AD=12cm,点P在AD边上以每秒1cm的速度从点A向点D运动,点Q在BC边上,以每秒4cm的速度从点C出发,在CB间往返运动,两个点同时出发,当点P到达点D时停止(同时点Q也停止),在运动以后,以P、D、Q、B四点组成平行四边形的次数有 次.
15.如图,已知DE∥BC,AB∥CD,E为AB的中点,∠A=∠B.下列结论:
①AC=DE;②CD=AE;
③AC平分∠BCD;④O点是DE的中点;
⑤AC=AB.其中正确的番号有 .
16.如图, ABCD的对角线AC恰好平分∠DAB,点H、点F分别在AD、BC上,点E、点G分别在BA、DC的延长线上,且AE=AH=CG=CF.
(1)求证:四边形EFGH为平行四边形.
(2)写出△HEA和四边形EFGH的面积之间的数量关系,并说明理由.
17.已知,如图,在平行四边形ABCD中,点G,H分别是AB,CD的中点,点E,F在对角线AC上,且AE=CF.
(1)求证:四边形EGFH是平行四边形.
(2)连接BD交AC于点O,若BD=12,AE=EF﹣CF,求EG的长.
18.如图,已知四边形ABCD是平行四边形,AE⊥BD于点E,CF⊥BD于点F,延长AE,CF分别交CD,AB于点M,N.
(1)求证:四边形CMAN是平行四边形;
(2)已知DE=4,FN=3,求△BFN的周长.
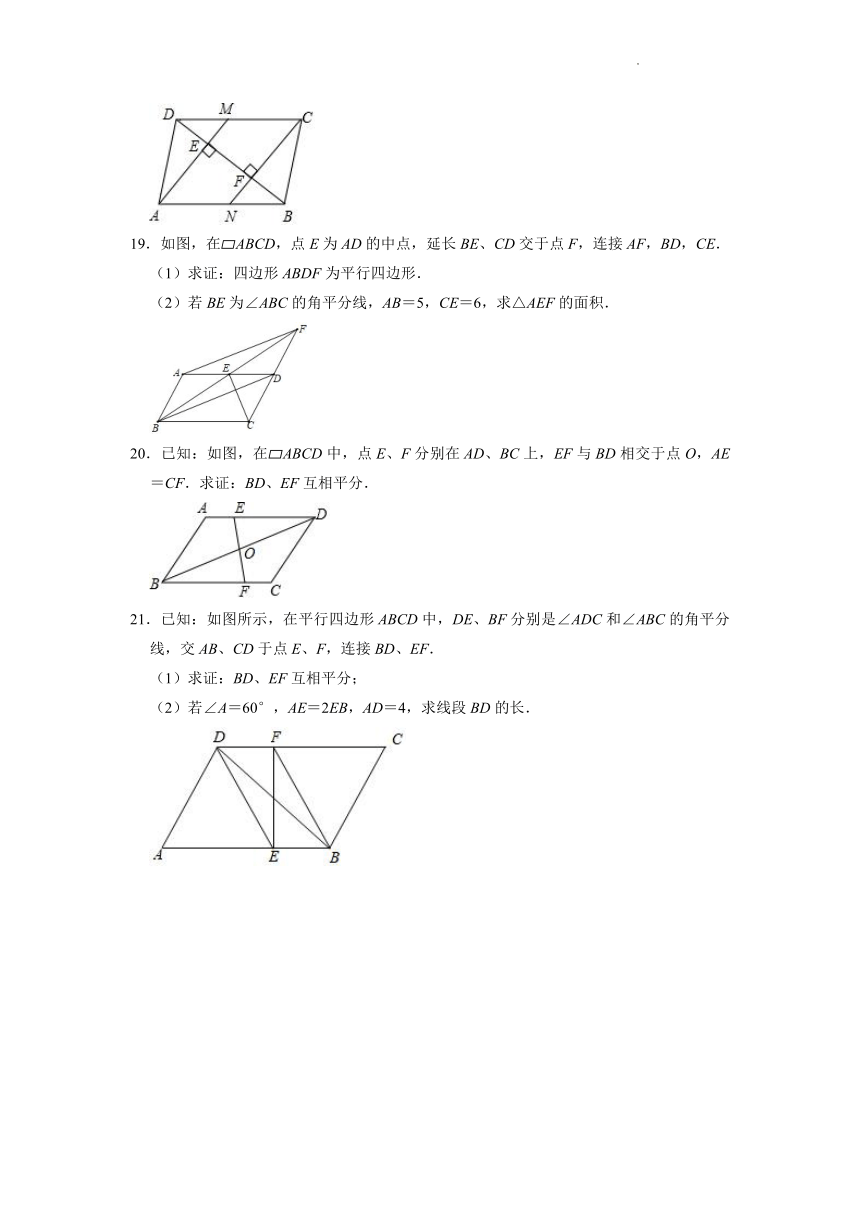
19.如图,在 ABCD,点E为AD的中点,延长BE、CD交于点F,连接AF,BD,CE.
(1)求证:四边形ABDF为平行四边形.
(2)若BE为∠ABC的角平分线,AB=5,CE=6,求△AEF的面积.
20.已知:如图,在 ABCD中,点E、F分别在AD、BC上,EF与BD相交于点O,AE=CF.求证:BD、EF互相平分.
21.已知:如图所示,在平行四边形ABCD中,DE、BF分别是∠ADC和∠ABC的角平分线,交AB、CD于点E、F,连接BD、EF.
(1)求证:BD、EF互相平分;
(2)若∠A=60°,AE=2EB,AD=4,求线段BD的长.
参考答案
一.平行四边形的性质
1.解:延长AB,过点C作CE⊥AB交于点E,
∵四边形ABCD是平行四边形,
∴AB=DC,BC=AD,DC∥AB,
∵DC∥AB,∠ABD=90°,
∴∠CDB=90°,
可得:∠CDB=∠DBC=∠BEC=90°,
则四边形DBEC是矩形,
∴DC=BE=AB,
设AB=BE=x,
∵AC2﹣AE2=CE2,BC2﹣BE2=CE2,
∴112﹣(2x)2=72﹣x2,
∴x=2.
∴AB=2
故答案为:2.
2.解:(1)∵点A(0,﹣2),点C(6,2),
∴线段AC中点E的坐标为(3,0),
故答案为:(3,0);
(2)∵点B(m,m+1),
∴点B在直线y=x+1上运动,
则直线y=x+1与x轴交于点F(﹣1,0),∠BFO=45°,
如图,当BE⊥直线y=x+1时,BE有最小值,即BD有最小值,
此时,EF=3﹣(﹣1)=4,
∵∠BFE=45°,∠EBF=90°,
∴∠BFE=∠BEF,
∴BE=BF,EF=BE,
∴BE=2,
∴BD的最小值=4,
故答案为4.
3.解:如图1,当∠ABC是锐角时,
在直角△ABE中,AB=5,AE=4,
由勾股定理得,BE=3,又EC=7,
∴BC=10,
∴ ABCD的周长等于30;
如图2,当∠ABC是钝角时,
在直角△ABE中,AB=5,AE=4,
由勾股定理得,BE=3,又EC=7,
∴BC=4,
∴ ABCD的周长等于18;
故答案为18或30.
4.解:(1)连接AC,如图,
∵平行四边形ABCD,
∴S△ABC=S△ACD,
即 BC AE=CD AF,
∵AE=6,AF=8,
∴3BC=4AF,
∴CD:BC=3:4,
故答案为:3:4.
(2)延长AF与BC延长线交于点M,过点M作MN⊥AE交AE的延长线于点N,如图,
∵平行四边形ABCD,
∴AD=BC,AD∥BM,
∴∠ADF=∠MCF,
∵F为CD的中点,
∴CF=DF,
在△AFD和△MFC,
,
∴△AFD≌△MFC(ASA),
∴AD=CM,AF=FM,
∴AM=2AF=16,
∵∠EAF=60°,∠N=90°,
∴∠AMN=30°,
∴AN=AM=8,MN==8,
∵AE=6,
∴EN=AN﹣AE=2,
∴EM==14,
∵E为BC中点,
∴EC==AD=,
∴EM=EC+CM=CM=AD,
∴AD=EM=,
故答案为:.
5.解:过点D作DE⊥AB于E,
∵四边形ABCD是平行四边形
∴AD=BC=2,
∵∠A=45°,DE⊥AB,
∴∠A=∠ADE=45°,
∴DE=AE,
∵DE2+AE2=AD2=4,
∴DE=,
故答案为.
6.解:如图,过点F作FM⊥AE于点M,过点M作MG∥AB交BC于点G,连接EF,
∵∠EAF=45°,
∴△AMF是等腰直角三角形,
∴AM=MF=AF=2,
∵AE=4,
∴EM=AE﹣AM=2,
∴AM=EM,
∵MG∥AB,
∴BG=GE,
∴GM是三角形AEB的中位线,
∴GM∥AB,GM=AB,
∴GM=CD,
∵点F是CD边的中点,
∴CF=CD,
∴GM∥CF,GM=CF,
∴四边形GMFC是平行四边形,
∴GC=MF=2,
∵BE=2BG=2GE,BE=2CE,
∴BG=GE=EC,
∴BE=GC=2,
∵FM⊥AE,FM∥GC,
∴AE⊥GC,
∵AE=4,
∴AB===2.
故答案为:2.
7.解:∵四边形ABCD是平行四边形,
∴AD∥BC,∠B=∠D,
∴∠DAE+∠AEC=180°,
∵∠AEC=90°,∠EAF=45°,
∴∠EAD=90°,∠AGE=45°,
∴∠FAD=45°,
∵AF⊥CD,
∴∠AFD=90°,
∴∠D=45°,
∴△ABE和△AFD都是等腰直角三角形,
∵AE+AF=5,
∴设AE=x,则AF=5﹣x,
∴AB=x,AD=(5﹣x),
∴平行四边形ABCD的周长为:[x+(5﹣x)]×2=10,
故答案为:10.
8.解:∵四边形ABCD是平行四边形,EF∥BC,HG∥AB,
∴AD=BC,AB=CD,AB∥GH∥CD,AD∥EF∥BC,
∴四边形HBEM、GMFD是平行四边形,
在△ABD和△CDB中,
,
∴△ABD≌△CDB(SSS),
即△ABD和△CDB的面积相等;
同理△BEM和△MHB的面积相等,△GMD和△FDM的面积相等,
故四边形AEMG和四边形HCFM的面积相等,即S1=S2.
故答案为:S1=S2.
二.平行四边形的判定
9.解:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,AB∥CD,
∴∠DAE=∠BCF,∠DCF=∠BAE,
①DE=BF时,不能证明△ADE≌△CBF,
不能证明四边形DEBF是平行四边形;
②∠ADE=∠CBF时,
在△ADE和△CBF中,,
∴△ADE≌△CBF(ASA),
∴DE=BF,∠AED=∠CFB,
∴∠DEF=∠BFE,
∴DE∥BF,
∴四边形DEBF是平行四边形;
③AF=CE时,AE=CF,
在△ADE和△CBF中,,
∴△ADE≌△CBF(SAS),
∴DE=BF,∠AED=∠CFB,
∴∠DEF=∠BFE,
∴DE∥BF,
∴四边形DEBF是平行四边形;
④∠AEB=∠CFD时,
在△ABE和△CDF中,,
∴△ABE≌△CDF(AAS),
∴BE=DF,
∵∠AEB=∠CFD,
∴∠BEF=∠DFE,
∴BE∥DF,
∴四边形DEBF是平行四边形;
故答案为:②③④.
10.解:分别以AB、AC、BC为对角线画图即可,
如图所示,第四个顶点不可能在第三象限,
故答案为:三.
11.解:如图所示,
当AB为边,①即当四边形ABQ2P2是平行四边形,所以AB=P2Q2,AP2=BQ2,
∴Q2点的坐标是:(0,﹣6),
②当四边形QPBA是平行四边形,所以AB=PQ,QA=PB,
∴Q点的坐标是:(0,6),
当AB为对角线,即当四边形P1AQ1B是平行四边形,所以AP1=Q1B,
AQ1=BP1,
∴Q1点的坐标是:(0,﹣2).
故答案为:(0,﹣6)或(0,﹣2)或(0,6).
三.平行四边形的判定与性质
12.解:①∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,OB=OD,OA=OC,
∵BF=DE,
∴BF﹣OB=DE﹣OD,
即OF=OE,
∴四边形AECF是平行四边形;
③∵AB∥CD,
∴∠ABE=∠CDF,
∵∠BAE=∠DCF,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(ASA),
∴BE=DF,
∵AO=CO,BO=DO,
∴OE=OF,
∴四边形AECF是平行四边形;
④∵AF∥CE,
∴∠AFB=∠CED,
在△ABF和△CDE中,
,
∴△ABF≌△CDE(AAS),
∴BF=DE,
∴BF﹣OB=DE﹣OD,
即OF=OE,
又∵OA=OC,
∴四边形AECF是平行四边形;
②∵AE=CF,不能判定△ABE≌△CDF,
∴不能判定四边形AECF是平行四边形;
∴一定能判定四边形AECF是平行四边形的是①③④,
故答案为:①③④.
13.解:如图,∵∠DAC=∠BCA,∠DCA=∠BAC,
∴AD∥BC,AB∥CD,
∴四边形ABCD是平行四边形,
∴∠B=∠D=52°.
故答案为:52°.
14.解:设经过t秒,以点P、D、Q、B为顶点组成平行四边形,
∵以点P、D、Q、B为顶点组成平行四边形,
∴DP=BQ,
分为以下情况:①点Q的运动路线是C﹣B,方程为12﹣4t=12﹣t,
此时方程t=0,此时不符合题意;
②点Q的运动路线是C﹣B﹣C,方程为4t﹣12=12﹣t,
解得:t=4.8;
③点Q的运动路线是C﹣B﹣C﹣B,方程为12﹣(4t﹣24)=12﹣t,
解得:t=8;
④点Q的运动路线是C﹣B﹣C﹣B﹣C,方程为4t﹣36=12﹣t,
解得:t=9.6;
∴共3次.
故答案为:3.
15.解:∵已知DE∥BC,AB∥CD,
∴四边形BCDE为平行四边形,
∴CB=DE;
∵∠A=∠B,
∴AC=BC,
∴AC=DE,即可得①正确;
根据平行线等分线段性质可得AO=CO,
∵AB∥CD,
∴∠A=∠DCO,
又∵∠AOE=∠COD,
∴△AOE≌△COD(ASA),
∴AE=CD,即可得②正确;OE=OD,O点是DE的中点;即可得④正确;
结论③⑤无法证明.
故答案填:①②④.
16.(1)证明:∵四边形ABCD是平行四边形,
∴DC=AB,AD=BC,∠B=∠D,
∵AE=AH=CG=CF,
∴AB+AE=CD+CG,BC﹣CF=AD﹣AH,
即EB=GD,BF=DH,
在△BFE和△DHG中,
,
∴△BFE≌△DHG(SAS),
∴EF=GH,
∵∠DAB=∠DCB,
∴∠EAH=∠FCG,
同理△EAH≌△GCF(SAS),
∴EH=FG,
∴四边形EFGH是平行四边形;
(2)解:△AEH的面积=平行四边形EFGH的面积,理由如下:
如图,设AC与GH交于点P,连接PE、PF,
∵AH=AE=CF=CG,∠BAD=∠AEH+∠AHE,AC平分∠DAB,
∴∠AEH=∠AHE=∠DAC=∠BAC,
∴EH∥AP,
∴△AEH的面积=△PEH的面积,
同理可得:△GCF的面积=△PFG的面积,
由(1)得:△EAH≌△GCF,
∴△EAH的面积=△GCF的面积,
∴△AEH的面积+△PFG的面积=2△AEH的面积=平行四边形EFGH的面积,
∴△AEH的面积=平行四边形EFGH的面积.
17.(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠GAE=∠HCF,
∵点G,H分别是AB,CD的中点,
∴AG=CH,
在△AGE和△CHF中,
,
∴△AGE≌△CHF(SAS),
∴GE=HF,∠AEG=∠CFH,
∴∠GEF=∠HFE,
∴GE∥HF,
又∵GE=HF,
∴四边形EGFH是平行四边形;
(2)解:连接BD交AC于点O,如图:
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵BD=12,
∴OB=OD=6,
∵AE=CF,OA=OC,
∴OE=OF,
∵AE=EF﹣CF,
∴AE+CF=EF,AE=CF,
∴2AE=EF=2OE,
∴AE=OE,
又∵点G是AB的中点,
∴EG是△ABO的中位线,
∴EG=OB=3.
18.(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,
∵AM⊥BD,CN⊥BD,
∴AM∥CN,
∴四边形CMAN是平行四边形;
(2)解:∵四边形CMAN是平行四边形,
∴AN=CM,
∵CD=AB,
∴DM=BN,
∵CD∥AB,
∴∠MDE=∠NBF,
在△BNF和△DME中,
,
∴△DME≌△BNF(AAS),
∴BF=DE=4,
在Rt△BFN中,BN===5,
∴△BFN的周长=FN+BF+BN=3+4+5=12.
19.解:(1)证明:由题意得,AB∥CF,
∴∠ABE=∠DFE,
又∵点E为AD的中点,
∴AE=DE,
在△ABE和△DFE中,
,
∴△ABE≌△DFE(AAS)
∴AB=DF,
又∵AB∥DF,
∴四边形ABDF为平行四边形(一组对边平行且相等的四边形是平行四边形);
(2)过点F作AD的垂线交AD延长线于点K,过点D作DH⊥EC,过点E作EG⊥CD,
∵S△AEF=;,
∴S△AEF=S△EDF,
又∵BE为∠ABC的角平分线,
∴∠ABE=∠EBC,
又∵AD∥BC,
∴∠EBC=∠FED,
而∠ABE=∠DFE,
∴∠FED=∠DFE,
∴ED=FD,
由(1)可知AB=DC=FD=5,
∴ED=FD=DC=5,
又∵S△EFD=,S△EDC=,
∴S△AEF=S△EDF=S△ECD,
在等腰△EDC中,ED=CD=5,EC=6,
∵DH⊥EC,
∴EH===3,
在Rt△EHD中,ED=5,EH=3,
∴DH===4,
∴S△ECD==12,
∴S△AEF=S△EDF=S△ECD=12,
故S△AEF=12.
20.证明:连接BE、DF,如图所示:
∵四边形ABCD为平行四边形,
∴AD=BC,AD∥BC,
又∵AE=CF,
∴DE=BF,
∴四边形EBFD为平行四边形,
∴BD、EF互相平分.
21.(1)证明:∵四边形ABCD是平行四边形,
∴CD∥AB,CD=AB,AD=BC,
∵DE、BF分别是∠ADC和∠ABC的角平分线,
∴∠ADE=∠CDE,∠CBF=∠ABF,
∵CD∥AB,
∴∠AED=∠CDE,∠CFB=∠ABF,
∴∠AED=∠ADE,∠CFB=∠CBF,
∴AE=AD,CF=CB,
∴AE=CF,
∴AB﹣AE=CD﹣CF 即BE=DF,
∵DF∥BE,
∴四边形DEBF是平行四边形.
∴BD、EF互相平分;
(2)∵∠A=60°,AE=AD,
∴△ADE是等边三角形,
∵AD=4,
∴DE=AE=4,
∵AE=2EB,
∴BE=GE=2,
∴BG=4,
过D点作DG⊥AB于点G,
在Rt△ADG中,AD=4,∠A=60°,
∴AG=AD=2,
∴DG==2,
∴BD===2.
一.平行四边形的性质
1.如图,在 ABCD中,AC=11,BC=7,BD⊥AB,则AB= .
2.在平面直角坐标系xOy中,已知四边形ABCD是平行四边形,且点A(0,﹣2),点B(m,m+1),点C(6,2).
(1)线段AC的中点E的坐标为 ;
(2)对角线BD长的最小值为 .
3.在平行四边形ABCD中,BC边上的高为AE=4,AB=5,EC=7,则平行四边形ABCD的周长等于 .
4.如图,在平行四边形ABCD中,∠B<90°,BC>AB,点E、F分别在边BC和CD上,AE=6,AF=8,∠EAF=60°.
(1)若AE⊥BC,AF⊥CD,则CD:BC= ;
(2)若点E、F在分别是边BC和CD的中点,则AD= .
5.在平行四边形ABCD中,∠A=45°,BC=2,则AB与CD之间的距离为 .
6.如图所示,在 ABCD中,点E在线段BC上且BE=2CE,点F是CD边的中点,若AE=4,AF=4,且∠EAF=45°,则AB的长是 .
7.如图,在 ABCD中,AE⊥BC于E,AF⊥CD于F,∠EAF=45°,且AE+AF=5,则平行四边形ABCD的周长为 .
8.如图,过平行四边形ABCD的对角找BD上一点M分别作平行四边形两边的平行线EF与GH,那么图中的平行四边形AEMG的面积S1与平行四边形HCFM的面积S2的大小关系是 .
二.平行四边形的判定
9.如图,点E,F是 ABCD对角线上两点,在条件:①DE=BF;②∠ADE=∠CBF;③AF=CE;④∠AEB=∠CFD中,选择一个条件添加,使四边形DEBF是平行四边形可添加的条件有 (写出所有正确条件的序号)
10.若以A(﹣0.5,0),B(2,0),C(0,1)三点为顶点要画平行四边形,则第四个顶点不可能在第 象限.
11.在平面直角坐标系xOy中,有A(3,2),B(﹣1,﹣4),P是x轴上的一点,Q是y轴上的一点,若以点A,B,P,Q四个点为顶点的四边形是平行四边形,则Q点的坐标是 .
三.平行四边形的判定与性质
12.如图,在 ABCD中,AC,BD相交于点O,点E,F在对角线BD上,有下列条件:①BF=DE;②AE=CF;③∠EAB=∠FCD;④AF∥CE.其中一定能判定四边形AECF是平行四边形的是 .
13.四边形ABCD中,若∠DAC=∠BCA,∠DCA=∠BAC,且∠D=52°,则∠B= .
14.如图,平行四边形ABCD中,AB=8cm,AD=12cm,点P在AD边上以每秒1cm的速度从点A向点D运动,点Q在BC边上,以每秒4cm的速度从点C出发,在CB间往返运动,两个点同时出发,当点P到达点D时停止(同时点Q也停止),在运动以后,以P、D、Q、B四点组成平行四边形的次数有 次.
15.如图,已知DE∥BC,AB∥CD,E为AB的中点,∠A=∠B.下列结论:
①AC=DE;②CD=AE;
③AC平分∠BCD;④O点是DE的中点;
⑤AC=AB.其中正确的番号有 .
16.如图, ABCD的对角线AC恰好平分∠DAB,点H、点F分别在AD、BC上,点E、点G分别在BA、DC的延长线上,且AE=AH=CG=CF.
(1)求证:四边形EFGH为平行四边形.
(2)写出△HEA和四边形EFGH的面积之间的数量关系,并说明理由.
17.已知,如图,在平行四边形ABCD中,点G,H分别是AB,CD的中点,点E,F在对角线AC上,且AE=CF.
(1)求证:四边形EGFH是平行四边形.
(2)连接BD交AC于点O,若BD=12,AE=EF﹣CF,求EG的长.
18.如图,已知四边形ABCD是平行四边形,AE⊥BD于点E,CF⊥BD于点F,延长AE,CF分别交CD,AB于点M,N.
(1)求证:四边形CMAN是平行四边形;
(2)已知DE=4,FN=3,求△BFN的周长.
19.如图,在 ABCD,点E为AD的中点,延长BE、CD交于点F,连接AF,BD,CE.
(1)求证:四边形ABDF为平行四边形.
(2)若BE为∠ABC的角平分线,AB=5,CE=6,求△AEF的面积.
20.已知:如图,在 ABCD中,点E、F分别在AD、BC上,EF与BD相交于点O,AE=CF.求证:BD、EF互相平分.
21.已知:如图所示,在平行四边形ABCD中,DE、BF分别是∠ADC和∠ABC的角平分线,交AB、CD于点E、F,连接BD、EF.
(1)求证:BD、EF互相平分;
(2)若∠A=60°,AE=2EB,AD=4,求线段BD的长.
参考答案
一.平行四边形的性质
1.解:延长AB,过点C作CE⊥AB交于点E,
∵四边形ABCD是平行四边形,
∴AB=DC,BC=AD,DC∥AB,
∵DC∥AB,∠ABD=90°,
∴∠CDB=90°,
可得:∠CDB=∠DBC=∠BEC=90°,
则四边形DBEC是矩形,
∴DC=BE=AB,
设AB=BE=x,
∵AC2﹣AE2=CE2,BC2﹣BE2=CE2,
∴112﹣(2x)2=72﹣x2,
∴x=2.
∴AB=2
故答案为:2.
2.解:(1)∵点A(0,﹣2),点C(6,2),
∴线段AC中点E的坐标为(3,0),
故答案为:(3,0);
(2)∵点B(m,m+1),
∴点B在直线y=x+1上运动,
则直线y=x+1与x轴交于点F(﹣1,0),∠BFO=45°,
如图,当BE⊥直线y=x+1时,BE有最小值,即BD有最小值,
此时,EF=3﹣(﹣1)=4,
∵∠BFE=45°,∠EBF=90°,
∴∠BFE=∠BEF,
∴BE=BF,EF=BE,
∴BE=2,
∴BD的最小值=4,
故答案为4.
3.解:如图1,当∠ABC是锐角时,
在直角△ABE中,AB=5,AE=4,
由勾股定理得,BE=3,又EC=7,
∴BC=10,
∴ ABCD的周长等于30;
如图2,当∠ABC是钝角时,
在直角△ABE中,AB=5,AE=4,
由勾股定理得,BE=3,又EC=7,
∴BC=4,
∴ ABCD的周长等于18;
故答案为18或30.
4.解:(1)连接AC,如图,
∵平行四边形ABCD,
∴S△ABC=S△ACD,
即 BC AE=CD AF,
∵AE=6,AF=8,
∴3BC=4AF,
∴CD:BC=3:4,
故答案为:3:4.
(2)延长AF与BC延长线交于点M,过点M作MN⊥AE交AE的延长线于点N,如图,
∵平行四边形ABCD,
∴AD=BC,AD∥BM,
∴∠ADF=∠MCF,
∵F为CD的中点,
∴CF=DF,
在△AFD和△MFC,
,
∴△AFD≌△MFC(ASA),
∴AD=CM,AF=FM,
∴AM=2AF=16,
∵∠EAF=60°,∠N=90°,
∴∠AMN=30°,
∴AN=AM=8,MN==8,
∵AE=6,
∴EN=AN﹣AE=2,
∴EM==14,
∵E为BC中点,
∴EC==AD=,
∴EM=EC+CM=CM=AD,
∴AD=EM=,
故答案为:.
5.解:过点D作DE⊥AB于E,
∵四边形ABCD是平行四边形
∴AD=BC=2,
∵∠A=45°,DE⊥AB,
∴∠A=∠ADE=45°,
∴DE=AE,
∵DE2+AE2=AD2=4,
∴DE=,
故答案为.
6.解:如图,过点F作FM⊥AE于点M,过点M作MG∥AB交BC于点G,连接EF,
∵∠EAF=45°,
∴△AMF是等腰直角三角形,
∴AM=MF=AF=2,
∵AE=4,
∴EM=AE﹣AM=2,
∴AM=EM,
∵MG∥AB,
∴BG=GE,
∴GM是三角形AEB的中位线,
∴GM∥AB,GM=AB,
∴GM=CD,
∵点F是CD边的中点,
∴CF=CD,
∴GM∥CF,GM=CF,
∴四边形GMFC是平行四边形,
∴GC=MF=2,
∵BE=2BG=2GE,BE=2CE,
∴BG=GE=EC,
∴BE=GC=2,
∵FM⊥AE,FM∥GC,
∴AE⊥GC,
∵AE=4,
∴AB===2.
故答案为:2.
7.解:∵四边形ABCD是平行四边形,
∴AD∥BC,∠B=∠D,
∴∠DAE+∠AEC=180°,
∵∠AEC=90°,∠EAF=45°,
∴∠EAD=90°,∠AGE=45°,
∴∠FAD=45°,
∵AF⊥CD,
∴∠AFD=90°,
∴∠D=45°,
∴△ABE和△AFD都是等腰直角三角形,
∵AE+AF=5,
∴设AE=x,则AF=5﹣x,
∴AB=x,AD=(5﹣x),
∴平行四边形ABCD的周长为:[x+(5﹣x)]×2=10,
故答案为:10.
8.解:∵四边形ABCD是平行四边形,EF∥BC,HG∥AB,
∴AD=BC,AB=CD,AB∥GH∥CD,AD∥EF∥BC,
∴四边形HBEM、GMFD是平行四边形,
在△ABD和△CDB中,
,
∴△ABD≌△CDB(SSS),
即△ABD和△CDB的面积相等;
同理△BEM和△MHB的面积相等,△GMD和△FDM的面积相等,
故四边形AEMG和四边形HCFM的面积相等,即S1=S2.
故答案为:S1=S2.
二.平行四边形的判定
9.解:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,AB∥CD,
∴∠DAE=∠BCF,∠DCF=∠BAE,
①DE=BF时,不能证明△ADE≌△CBF,
不能证明四边形DEBF是平行四边形;
②∠ADE=∠CBF时,
在△ADE和△CBF中,,
∴△ADE≌△CBF(ASA),
∴DE=BF,∠AED=∠CFB,
∴∠DEF=∠BFE,
∴DE∥BF,
∴四边形DEBF是平行四边形;
③AF=CE时,AE=CF,
在△ADE和△CBF中,,
∴△ADE≌△CBF(SAS),
∴DE=BF,∠AED=∠CFB,
∴∠DEF=∠BFE,
∴DE∥BF,
∴四边形DEBF是平行四边形;
④∠AEB=∠CFD时,
在△ABE和△CDF中,,
∴△ABE≌△CDF(AAS),
∴BE=DF,
∵∠AEB=∠CFD,
∴∠BEF=∠DFE,
∴BE∥DF,
∴四边形DEBF是平行四边形;
故答案为:②③④.
10.解:分别以AB、AC、BC为对角线画图即可,
如图所示,第四个顶点不可能在第三象限,
故答案为:三.
11.解:如图所示,
当AB为边,①即当四边形ABQ2P2是平行四边形,所以AB=P2Q2,AP2=BQ2,
∴Q2点的坐标是:(0,﹣6),
②当四边形QPBA是平行四边形,所以AB=PQ,QA=PB,
∴Q点的坐标是:(0,6),
当AB为对角线,即当四边形P1AQ1B是平行四边形,所以AP1=Q1B,
AQ1=BP1,
∴Q1点的坐标是:(0,﹣2).
故答案为:(0,﹣6)或(0,﹣2)或(0,6).
三.平行四边形的判定与性质
12.解:①∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,OB=OD,OA=OC,
∵BF=DE,
∴BF﹣OB=DE﹣OD,
即OF=OE,
∴四边形AECF是平行四边形;
③∵AB∥CD,
∴∠ABE=∠CDF,
∵∠BAE=∠DCF,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(ASA),
∴BE=DF,
∵AO=CO,BO=DO,
∴OE=OF,
∴四边形AECF是平行四边形;
④∵AF∥CE,
∴∠AFB=∠CED,
在△ABF和△CDE中,
,
∴△ABF≌△CDE(AAS),
∴BF=DE,
∴BF﹣OB=DE﹣OD,
即OF=OE,
又∵OA=OC,
∴四边形AECF是平行四边形;
②∵AE=CF,不能判定△ABE≌△CDF,
∴不能判定四边形AECF是平行四边形;
∴一定能判定四边形AECF是平行四边形的是①③④,
故答案为:①③④.
13.解:如图,∵∠DAC=∠BCA,∠DCA=∠BAC,
∴AD∥BC,AB∥CD,
∴四边形ABCD是平行四边形,
∴∠B=∠D=52°.
故答案为:52°.
14.解:设经过t秒,以点P、D、Q、B为顶点组成平行四边形,
∵以点P、D、Q、B为顶点组成平行四边形,
∴DP=BQ,
分为以下情况:①点Q的运动路线是C﹣B,方程为12﹣4t=12﹣t,
此时方程t=0,此时不符合题意;
②点Q的运动路线是C﹣B﹣C,方程为4t﹣12=12﹣t,
解得:t=4.8;
③点Q的运动路线是C﹣B﹣C﹣B,方程为12﹣(4t﹣24)=12﹣t,
解得:t=8;
④点Q的运动路线是C﹣B﹣C﹣B﹣C,方程为4t﹣36=12﹣t,
解得:t=9.6;
∴共3次.
故答案为:3.
15.解:∵已知DE∥BC,AB∥CD,
∴四边形BCDE为平行四边形,
∴CB=DE;
∵∠A=∠B,
∴AC=BC,
∴AC=DE,即可得①正确;
根据平行线等分线段性质可得AO=CO,
∵AB∥CD,
∴∠A=∠DCO,
又∵∠AOE=∠COD,
∴△AOE≌△COD(ASA),
∴AE=CD,即可得②正确;OE=OD,O点是DE的中点;即可得④正确;
结论③⑤无法证明.
故答案填:①②④.
16.(1)证明:∵四边形ABCD是平行四边形,
∴DC=AB,AD=BC,∠B=∠D,
∵AE=AH=CG=CF,
∴AB+AE=CD+CG,BC﹣CF=AD﹣AH,
即EB=GD,BF=DH,
在△BFE和△DHG中,
,
∴△BFE≌△DHG(SAS),
∴EF=GH,
∵∠DAB=∠DCB,
∴∠EAH=∠FCG,
同理△EAH≌△GCF(SAS),
∴EH=FG,
∴四边形EFGH是平行四边形;
(2)解:△AEH的面积=平行四边形EFGH的面积,理由如下:
如图,设AC与GH交于点P,连接PE、PF,
∵AH=AE=CF=CG,∠BAD=∠AEH+∠AHE,AC平分∠DAB,
∴∠AEH=∠AHE=∠DAC=∠BAC,
∴EH∥AP,
∴△AEH的面积=△PEH的面积,
同理可得:△GCF的面积=△PFG的面积,
由(1)得:△EAH≌△GCF,
∴△EAH的面积=△GCF的面积,
∴△AEH的面积+△PFG的面积=2△AEH的面积=平行四边形EFGH的面积,
∴△AEH的面积=平行四边形EFGH的面积.
17.(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠GAE=∠HCF,
∵点G,H分别是AB,CD的中点,
∴AG=CH,
在△AGE和△CHF中,
,
∴△AGE≌△CHF(SAS),
∴GE=HF,∠AEG=∠CFH,
∴∠GEF=∠HFE,
∴GE∥HF,
又∵GE=HF,
∴四边形EGFH是平行四边形;
(2)解:连接BD交AC于点O,如图:
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵BD=12,
∴OB=OD=6,
∵AE=CF,OA=OC,
∴OE=OF,
∵AE=EF﹣CF,
∴AE+CF=EF,AE=CF,
∴2AE=EF=2OE,
∴AE=OE,
又∵点G是AB的中点,
∴EG是△ABO的中位线,
∴EG=OB=3.
18.(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,
∵AM⊥BD,CN⊥BD,
∴AM∥CN,
∴四边形CMAN是平行四边形;
(2)解:∵四边形CMAN是平行四边形,
∴AN=CM,
∵CD=AB,
∴DM=BN,
∵CD∥AB,
∴∠MDE=∠NBF,
在△BNF和△DME中,
,
∴△DME≌△BNF(AAS),
∴BF=DE=4,
在Rt△BFN中,BN===5,
∴△BFN的周长=FN+BF+BN=3+4+5=12.
19.解:(1)证明:由题意得,AB∥CF,
∴∠ABE=∠DFE,
又∵点E为AD的中点,
∴AE=DE,
在△ABE和△DFE中,
,
∴△ABE≌△DFE(AAS)
∴AB=DF,
又∵AB∥DF,
∴四边形ABDF为平行四边形(一组对边平行且相等的四边形是平行四边形);
(2)过点F作AD的垂线交AD延长线于点K,过点D作DH⊥EC,过点E作EG⊥CD,
∵S△AEF=;,
∴S△AEF=S△EDF,
又∵BE为∠ABC的角平分线,
∴∠ABE=∠EBC,
又∵AD∥BC,
∴∠EBC=∠FED,
而∠ABE=∠DFE,
∴∠FED=∠DFE,
∴ED=FD,
由(1)可知AB=DC=FD=5,
∴ED=FD=DC=5,
又∵S△EFD=,S△EDC=,
∴S△AEF=S△EDF=S△ECD,
在等腰△EDC中,ED=CD=5,EC=6,
∵DH⊥EC,
∴EH===3,
在Rt△EHD中,ED=5,EH=3,
∴DH===4,
∴S△ECD==12,
∴S△AEF=S△EDF=S△ECD=12,
故S△AEF=12.
20.证明:连接BE、DF,如图所示:
∵四边形ABCD为平行四边形,
∴AD=BC,AD∥BC,
又∵AE=CF,
∴DE=BF,
∴四边形EBFD为平行四边形,
∴BD、EF互相平分.
21.(1)证明:∵四边形ABCD是平行四边形,
∴CD∥AB,CD=AB,AD=BC,
∵DE、BF分别是∠ADC和∠ABC的角平分线,
∴∠ADE=∠CDE,∠CBF=∠ABF,
∵CD∥AB,
∴∠AED=∠CDE,∠CFB=∠ABF,
∴∠AED=∠ADE,∠CFB=∠CBF,
∴AE=AD,CF=CB,
∴AE=CF,
∴AB﹣AE=CD﹣CF 即BE=DF,
∵DF∥BE,
∴四边形DEBF是平行四边形.
∴BD、EF互相平分;
(2)∵∠A=60°,AE=AD,
∴△ADE是等边三角形,
∵AD=4,
∴DE=AE=4,
∵AE=2EB,
∴BE=GE=2,
∴BG=4,
过D点作DG⊥AB于点G,
在Rt△ADG中,AD=4,∠A=60°,
∴AG=AD=2,
∴DG==2,
∴BD===2.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
