2021-2022学年人教版八年级数学下册18.2.2菱形(判定)课时练习(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版八年级数学下册18.2.2菱形(判定)课时练习(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 669.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-21 12:05:23 | ||
图片预览


文档简介
菱形(判定)
一、单选题
1.在四边形ABCD中,对角线AC,BD互相平分,若添加一个条件使得四边形ABCD是菱形,则这个条件可以是( )
A.∠ABC=90° B.AC⊥BD C.AB=CD D.AB∥CD
2.下列关于菱形、矩形的说法正确的是( )
A.对角线相等的四边形是矩形
B.矩形的对角线相等且互相平分
C.对角线互相垂直的四边形是菱形
D.一组对边相等,另一组对边平行的四边形是菱形
3.如图,下列条件能使平行四边形ABCD是菱形的为( )
①AC⊥BD;②∠BAD=90°;③AB=BC;④AC=BD.
A.①③ B.②③ C.③④ D.①
4.已知四边形ABCD是平行四边形,对角线AC、BD交于点0,给出下列条件:(1)AB=AD;(2)AC=BD;(3)∠BOC=90°;(4)∠ABC=∠BCD;(5)∠ADB=∠CDB.其中能判定四边形ABCD是菱形的方法有( )
A.2种 B.3种 C.4种 D.5种
5.如图,下列条件:①;②;③;④,其中不能使平行四边形是菱形的是( )
A.① B.② C.③ D.④
6.如图,在△中,平分,交于点,交于点,若,则四边形的周长是( )
A.24 B.28 C.32 D.36
7.将图1所示的长方形纸片对折后得到图2,图2再对折后得到图3,沿图3中的虚线剪下并展开,所得的四边形是( )
A.矩形 B.菱形 C.正方形 D.梯形
8.如图,四边形ABCD中,AD∥BC,∠C=90°,AB=AD,连接BD,∠BAD的角平分线交BD、BC分别于点O、E,若EC=3,CD=4,则BO的长为( )
A.4 B.3 C.2 D.3
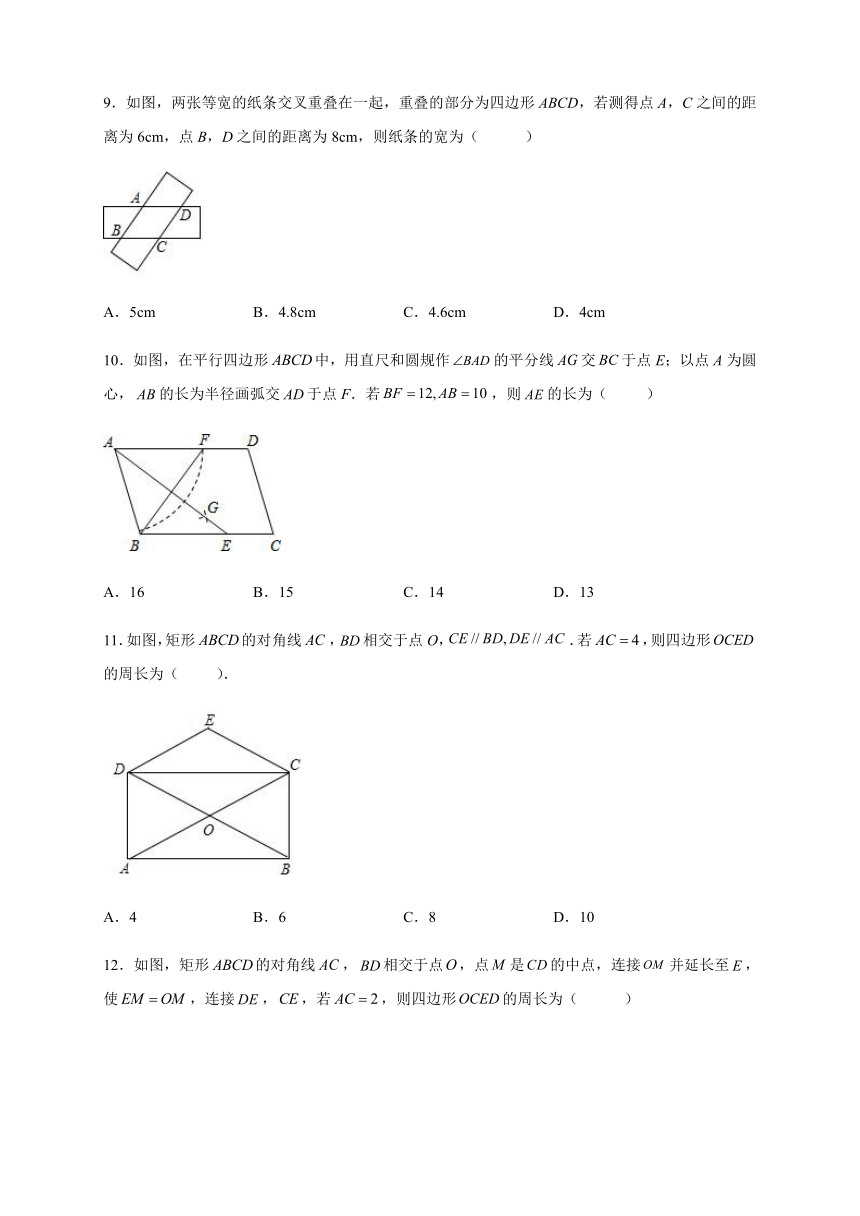
9.如图,两张等宽的纸条交叉重叠在一起,重叠的部分为四边形ABCD,若测得点A,C之间的距离为6cm,点B,D之间的距离为8cm,则纸条的宽为( )
A.5cm B.4.8cm C.4.6cm D.4cm
10.如图,在平行四边形中,用直尺和圆规作的平分线交于点E;以点A为圆心,的长为半径画弧交于点F.若,则的长为( )
A.16 B.15 C.14 D.13
11.如图,矩形的对角线,相交于点O,.若,则四边形的周长为( ).
A.4 B.6 C.8 D.10
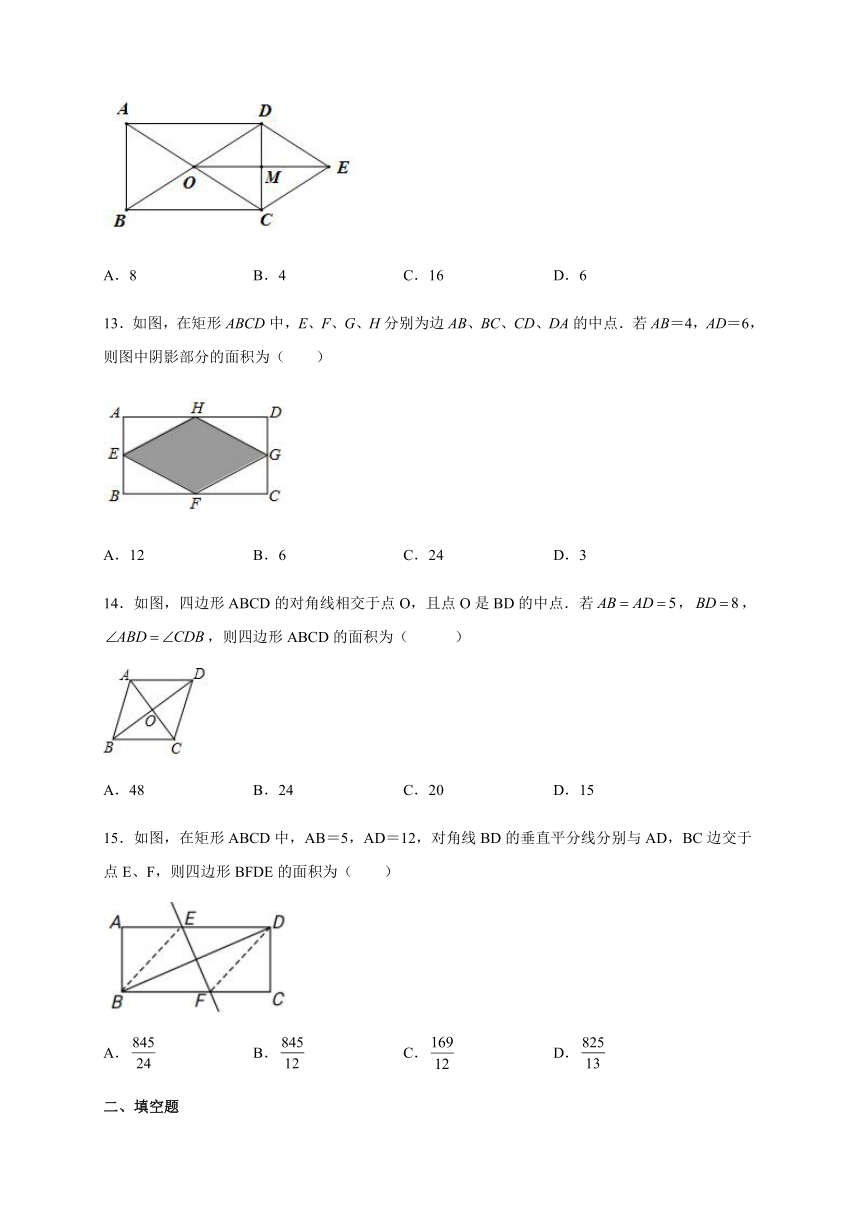
12.如图,矩形的对角线,相交于点,点是的中点,连接并延长至,使,连接,,若,则四边形的周长为( )
A.8 B.4 C.16 D.6
13.如图,在矩形ABCD中,E、F、G、H分别为边AB、BC、CD、DA的中点.若AB=4,AD=6,则图中阴影部分的面积为( )
A.12 B.6 C.24 D.3
14.如图,四边形ABCD的对角线相交于点O,且点O是BD的中点.若,,,则四边形ABCD的面积为( )
A.48 B.24 C.20 D.15
15.如图,在矩形ABCD中,AB=5,AD=12,对角线BD的垂直平分线分别与AD,BC边交于点E、F,则四边形BFDE的面积为( )
A. B. C. D.
二、填空题
16.△ABC中,延长BA至D使得AB=AD,延长CA至E使得AC=AE,当△ABC满足条件________时,四边形BCDE是菱形.
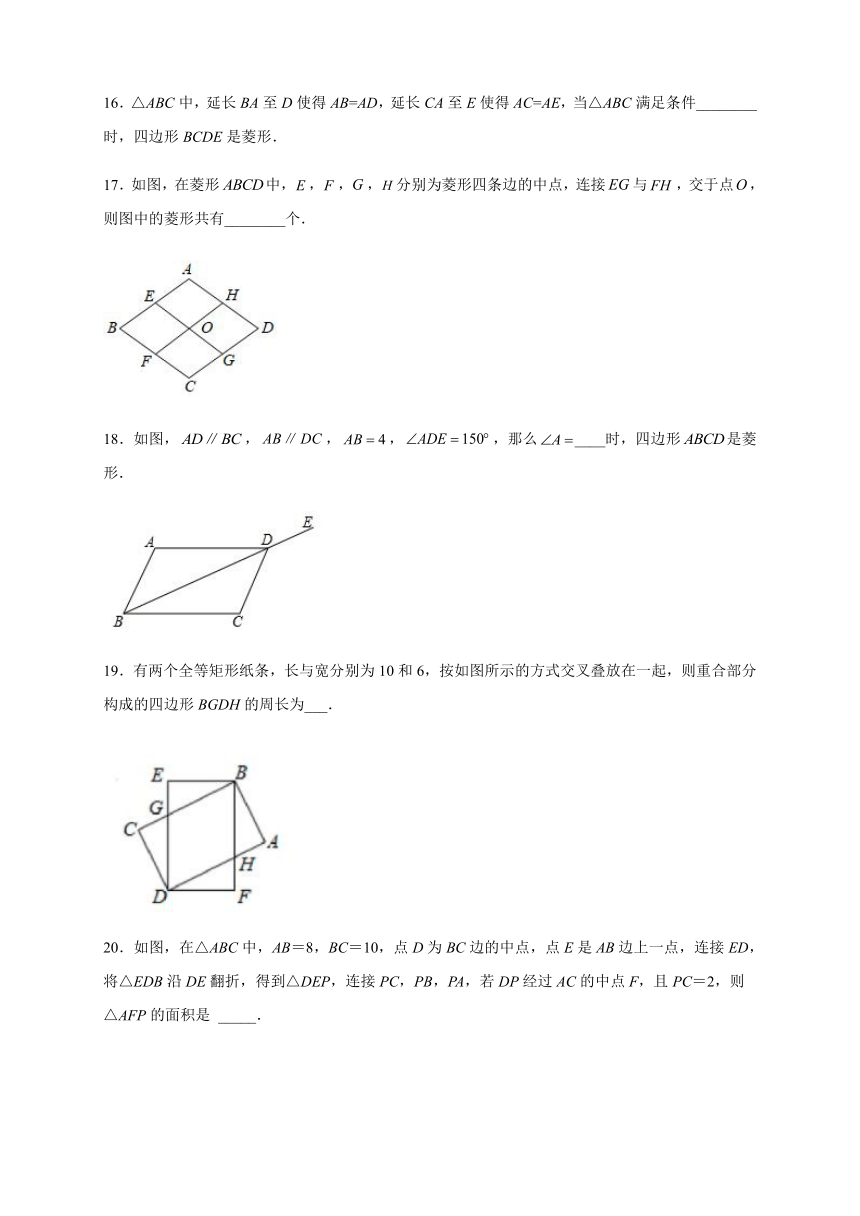
17.如图,在菱形中,,,,分别为菱形四条边的中点,连接与,交于点,则图中的菱形共有________个.
18.如图,,,,,那么____时,四边形是菱形.
19.有两个全等矩形纸条,长与宽分别为10和6,按如图所示的方式交叉叠放在一起,则重合部分构成的四边形BGDH的周长为___.
20.如图,在△ABC中,AB=8,BC=10,点D为BC边的中点,点E是AB边上一点,连接ED,将△EDB沿DE翻折,得到△DEP,连接PC,PB,PA,若DP经过AC的中点F,且PC=2,则△AFP的面积是 _____.
三、解答题
21.如图,在 ABCD中,点O是对角线BD的中点,过点O作EF⊥BD,垂足为点O,且交AD,BC分别于点E,F.
求证:四边形BEDF是菱形.
22.如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,BD是对角线,过A点作交CB的延长线于点G.
(1)求证:.
(2)若,求证:四边形DEBF是菱形.
23.如图,在四边形ABCD中,,,对角线AC、BD交于点O,AC平分∠BAD,过点C作交AB的延长线于点E.
(1)求证:四边形ABCD是菱形;
(2)若,,求CE的长.
24.如图,在平行四边形ABCD中,AE⊥BC于点E,AF⊥CD于点F,AE、AF分别交BD于点G、H.AG=AH.
(1)如图1,求证:平行四边形ABCD是菱形;
(2)如图2,当∠ABC=60°时,连接CH,在不添加任何辅助线的情况下,请直接写出图2中面积等于△BEG面积2倍的所有三角形.
25.如图,四边形ABCD中,AB=AD,∠B=∠D,AE⊥BC于E,AF⊥CD于F,连接EF.
(1)求证:△AEF是等腰三角形;
(2)若,求证:四边形ABCD为菱形.
26.两个不全等的直角三角形ABC和DEF重叠在一起,其中∠A=60°,AC=1.固定△ABC不动,将△DEF进行如下操作:
(1)如图(1),△DEF沿线段AB向右平移(D点在线段AB内移动),连接DC、CF、FB,四边形的形状在不断的变化,但它的面积不变化,请求出其面积;
(2)如图(2),当点移到的中点时,请你猜想四边形的形状,并说明理由.
试卷第1页,共3页
参考答案:
1.B
解:略
2.B
解:A、错误,对角线相等的平行四边形是矩形;
B、 正确,根据矩形的性质:矩形的对角线相等且互相平分;
C、错误,对角线互相垂直的平行四边形是菱形;
D、错误,一组对边相等,另一组对边平行的四边形可能是等腰梯形、平行四边形、矩形、菱形、正方形.
故选:B.
3.A
解:① ABCD中,AC⊥BD,根据对角线互相垂直的平行四边形是菱形,即可判定 ABCD是菱形;故①正确;
② ABCD中,∠BAD=90°,根据有一个角是直角的平行四边形是矩形,即可判定 ABCD是矩形,而不能判定 ABCD是菱形;故②错误;
③ ABCD中,AB=BC,根据一组邻边相等的平行四边形是菱形,即可判定 ABCD是菱形;故③正确;
④ ABCD中,AC=BD,根据对角线相等的平行四边形是矩形,即可判定 ABCD是矩形,而不能判定 ABCD是菱形;故④错误.
故正确的为①③
故选:A.
4.B
解:如图,四边形ABCD是平行四边形
(1)四边形ABCD是平行四边形,AB=AD
平行四边形ABCD是菱形;
(2)四边形ABCD是平行四边形,AC=BD
平行四边形ABCD是矩形;
(3) ∠BOC=90°
四边形ABCD是平行四边形
平行四边形ABCD是菱形;
(4)四边形ABCD是平行四边形
∠ABC=∠BCD
平行四边形ABCD是矩形;
(5)四边形ABCD是平行四边形
∠ADB=∠CDB
即
平行四边形ABCD是菱形.
其中,能判定四边形ABCD是菱形的方法有3种
故选:B.
5.A
解:①,对角线相等的平行四边形是矩形,故①符合题意;
②,对角线垂直的平行四边形是菱形,故②不符合题意;
③,邻边相等的平行四边形是菱形,故③不符合题意;
④,
∵,
∴,
∴,
∴,邻边相等的平行四边形是菱形,故④不符合题意;
故选:A.
6.C
解:∵
∴四边形是平行四边形
∴,
∵平分
∴
∴
∴平行四边形AEDF是菱形
∴
故选C.
7.B
解:
展得到的图形如上图,
由操作过程可知:AB=CD,BC=AD,
∴四边形ABCD是平行四边形,
∵AC⊥BD,
∴四边形ABCD为菱形,
故选:B.
8.C
解:连接DE.
在直角三角形CDE中,EC=3,CD=4,根据勾股定理,得DE=5.
∵AB=AD, AE平分
∴AE⊥BD,BO=OD,
∴AE垂直平分BD,∠BAE=∠DAE.
∴DE=BE=5.
∵AD∥BC,
∴∠DAE=∠AEB,
∴∠BAE=∠AEB,
∴AB=BE=5,
∴BC=BE+EC=8,
∴四边形ABED是菱形,
由勾股定理得出,
∴,
故选:C.
9.B
解:作AR⊥BC于R,AS⊥CD于S,连接AC、BD交于点O.
由题意知:AD∥BC,AB∥CD,
∴四边形ABCD是平行四边形,
∵两个矩形等宽,
∴AR=AS,
∵AR BC=AS CD,
∴BC=CD,
∴平行四边形ABCD是菱形,
∴AC⊥BD,
在Rt△AOB中,
∵OA=3cm,OB=4cm,
∴AB==5cm,
∵平行四边形ABCD是菱形,
∴AB=BC=5cm,
∴菱形ABCD的面积,即,
解得: cm.
故选:B.
10.A
解:如图,连接,设交于点,
平分
四边形是平行四边形
,
又
四边形是平行四边形
四边形是菱形
,
在中,,
故选A
11.C
解:,,
四边形是平行四边形,
四边形是矩形,,
,,,
,
四边形是菱形,
,
四边形的周长,
故选:C.
12.B
解:∵矩形的对角线,相交于点,
∴,
∴OC=OD=1,
∴△OCD是等腰三角形,
∵点是的中点,
∴OM是△OCD的中线,也是高,
∴OM⊥CD,DM=CM,
∵,
∴四边形OCED中,对角线OE与CD互相垂直且平分,
∴四边形OCED菱形,
∴四边形的周长为:;
故选:B.
13.A
解:连接AC,BD,FH,EG,
∵E,F,G,H分别为边AB,BC,CD,DA的中点,
∴AH=AD,BF=BC,
∵四边形ABCD是矩形,
∴AD=BC,ADBC,
∴AH=BF,AHBF,
∴四边形AHFB是平行四边形,
∴FH=AB=2,
同理EG=AD=4,
∵四边形ABCD是矩形,
∴AC=BD,
∵E,F,G,H分别为边AB,BC,CD,DA的中点,
∴HGAC,HG=AC,EFAC,EF=AC,EH=BD,
∴EH=HG,GH=EF,GHEF,
∴四边形EFGH是平行四边形,
∴平行四边形EFGH是菱形,
∴FH⊥EG,
∴阴影部分EFGH的面积是×HF×EG=×6×4=12,
故选:A.
14.B
解:∵AB=AD,点O是BD的中点,
∴AC⊥BD,∠BAO=∠DAO,
∵∠ABD=∠CDB,
∴AB∥CD,
∴∠BAC=∠ACD,
∴∠DAC=∠ACD,
∴AD=CD,
∴AB=CD,
∴四边形ABCD是菱形,
∵AB=5,BO=BD=4,
∴AO=3,
∴AC=2AO=6,
∴四边形ABCD的面积=×6×8=24,
故选:B.
15.A
解:∵四边形ABCD是矩形,
∴AD∥BC,
∴∠DEO=∠BFO,∠EDO=∠FBO,
∵对角线BD的垂直平分线分别与AD,BC边交于点E、F,
∴BO=DO,EF⊥BD,
∴△DEO≌△BFO(AAS),
∴EO=FO,
∵BO=DO,
∴四边形BEDF是平行四边形,
∵EF⊥BD,
∴平行四边形BEDF是菱形,
∴BE=DE,
∵AB=5,AD=12,∠A=90°,
∴BD=13,
设DE=x,则AE=12﹣x,
在Rt△AEB中,AB2+AE2=BE2,
即52+(12﹣x)2=x2,
∴x,
∴BE=DE,
在Rt△BEO中,OE,
∴EF=2EO,
∴菱形BEDF的面积,
故选:A.
16.∠BAC=90°
解:如图所示:∵AB=AD,EA=AC,
∴四边形EBCD是平行四边形;
当BD⊥EC时,四边形BCDE是菱形,
此时∠BAC=90°.
故答案为:∠BAC=90°.
17.5
解:∵四边形ABCD是菱形,E,F,F,H分别是菱形四边的中点,
∴AE=AH=HD=GD=CG=CF=FB=BE=OE=OG=OH=OF,
∴四边形AEOH,HOGD,EOFB,OFGC和ABCD均为菱形,共5个.
故答案为:5.
18.
解:当时,四边形是菱形,
证明:∵AD∥BC,AB∥CD,
∴四边形是平行四边形,
∵,
∴∠ADB=30°,
∵,
∴∠ABD=30°=∠ADB,
∴AB=AD,
∴四边形是菱形,
故答案为:.
19.##27.2
解:由题意得:矩形ABCD≌矩形BEDF,
∴∠A=90°,AB=BE=6,AD∥BC,BF∥DE,AD=10,
∴四边形BGDH是平行四边形,
∴平行四边形BGDH的面积=BG×AB=BH×BE,
∴BG=BH,
∴四边形BGDH是菱形,
∴BH=DH=DG=BG,
设BH=DH=x,则AH=10-x,
在Rt△ABH中,由勾股定理得:62+(10-x)2=x2,
解得:x=,
∴BH=,
∴四边形BGDH的周长=4BH=.
故答案为:
20.##
解:过点D作 DM⊥AB于点M,设ED与BP交于点O,
∵点D是BC边的中点,点F是AC的中点,
∴DP∥BE,
∴∠EBD=∠PDC,
又∵∠EPD=∠EBD,
∴∠EPD=∠PDC,
∴EP∥BD,
∴四边形BDPE为平行四边形,
又∵BD=DP,
∴平行四边形BDPE为菱形,
∴EP=BD=BE=DP=CD=5,BP⊥ED,
∴四边形 EPCD为平行四边形,
∴ED=PC=2,ED∥CP,
∵DP∥BE,即DP∥EG,
∴四边形EDPG是平行四边形,
∴EG=DP=5,PG=ED=2,
∴PG=CP,
∴PF是△ACG中位线,
∵AE=AB﹣BE=8﹣5=3,
∴AG=EG﹣AE=5﹣3=2,
∴PFAG=1,
在 Rt△BOE中,
BE=BD=5,EODE=1,
∴BO2,
∴S△BDEDE BO=2BE DM,
∴DM,
∵平行线间的距离相等,△AFP以PF为底,高即为,
∴S△AFPPF1,
故答案为:.
21.证明见解析
解:∵四边形ABCD是平行四边形,O为对角线BD的中点,
∴BO=DO,AD∥BC,
∴∠EDB=∠FBO,
在△EOD和△FOB中,,
∴△DOE≌△BOF(ASA);
∴OE=OF,
又∵OB=OD,
∴四边形BEDF是平行四边形,
∵EF⊥BD,
∴平行四边形BEDF为菱形.
22.(1)见解析 (2)见解析
(1)
∵四边形ABCD是平行四边形,
∴,,,
∵E、F分别为边AB、CD的中点,
∴,.
∴四边形DEBF是平行四边形,
∴.
(2)
∵,,
∴.
又∵F分别为边CD的中点,
∴.
∴平行四边形DEBF是菱形.
23.(1)见解析; (2)
(1)
证明:∵,
∴,
∵AC平分∠BAD,
∴,
∴,
∴,
∵AB=AD,
∴,
∵,
∴四边形ABCD是平行四边形,
又∵,
∴四边形ABCD是菱形;
(2)
∵四边形ABCD是菱形,BD=6,AC=8,
∴,,,
∴,
在中,根据勾股定理可知,
,
∴菱形的面积,
∵,
∴菱形面积,
∴.
24.(1)见解析;
(2)面积等于△BEG面积2倍的所有三角形有:△ABG,△ADH,△AGH,△DHC
(1)
证明:∵AG=AH,
∴∠AGH=∠AHG,
∵∠AGH=∠BGE,∠DHF=∠AHG,
∴∠BGE=∠DHF,
∵AE⊥BC,AF⊥CD,
∴∠BEG=∠DFH,
∴∠EBG=∠FDH,
∴∠CBD=∠CDB,
∴BC=CD,
∵四边形ABCD是平行四边形,
∴平行四边形ABCD是菱形;
(2)
解:面积等于△BEG面积2倍的三角形有:△ABG,△ADH,△AGH,△DHC,
∵四边形ABCD是菱形,∠ABC=60°,AE⊥BC,AF⊥CD,
∴∠DBC=∠ABD=∠BAE=∠DAF=30°,
设GE=a,
∴BG=2a,BE=a,
∵∠ABG=∠BAG=30°,
∴AG=BG=2a,
∴S△ABG=2S△BEG;
在△ABG和△ADH中,
,
∴△ABG≌△ADH(SAS),
同理△CDH≌△ADH(SAS),
∴△ABG≌△ADH≌△CDH,
∴S△ABG=S△ADH=S△CDH=2S△BEG;
∵∠GAH=120°-30°-30°=60°,AG=AH,
∴△AGH是等边三角形,
∴GH=AG=BG,
∴S△AGH=S△ABG=2S△BEG;
综上所述:面积等于△BEG面积2倍的所有三角形有:△ABG,△ADH,△AGH,△DHC.
25.(1)见解析 (2)见解析
(1)
证明:∵AE⊥BC,AF⊥CD,
∴∠AEB=∠AFD=90°,
在△ABE和△ADF中,
,
∴△ABE≌△ADF(AAS),
∴AE=AF,
∴△AEF是等腰三角形;
(2)
∵,
∴∠B+∠C=180°,
∵∠B=∠D,
∴∠D+∠C=180°,
∴,
∴四边形ABCD为平行四边形,
又∵AB=AD,
∴平行四边形ABCD为菱形.
26.(1) (2)四边形是菱形,理由见解析
(1)
解:过点作,垂足是点.
由题可知,,,
则四边形是梯形.
在直角中,,,,
,
在直角中,,,,
,,
.
;
(2)
证明:四边形是菱形.
理由如下:在直角中,是的中点,
,
由(1),
,
又,
四边形是平行四边形.
,
四边形是菱形.
答案第1页,共2页
一、单选题
1.在四边形ABCD中,对角线AC,BD互相平分,若添加一个条件使得四边形ABCD是菱形,则这个条件可以是( )
A.∠ABC=90° B.AC⊥BD C.AB=CD D.AB∥CD
2.下列关于菱形、矩形的说法正确的是( )
A.对角线相等的四边形是矩形
B.矩形的对角线相等且互相平分
C.对角线互相垂直的四边形是菱形
D.一组对边相等,另一组对边平行的四边形是菱形
3.如图,下列条件能使平行四边形ABCD是菱形的为( )
①AC⊥BD;②∠BAD=90°;③AB=BC;④AC=BD.
A.①③ B.②③ C.③④ D.①
4.已知四边形ABCD是平行四边形,对角线AC、BD交于点0,给出下列条件:(1)AB=AD;(2)AC=BD;(3)∠BOC=90°;(4)∠ABC=∠BCD;(5)∠ADB=∠CDB.其中能判定四边形ABCD是菱形的方法有( )
A.2种 B.3种 C.4种 D.5种
5.如图,下列条件:①;②;③;④,其中不能使平行四边形是菱形的是( )
A.① B.② C.③ D.④
6.如图,在△中,平分,交于点,交于点,若,则四边形的周长是( )
A.24 B.28 C.32 D.36
7.将图1所示的长方形纸片对折后得到图2,图2再对折后得到图3,沿图3中的虚线剪下并展开,所得的四边形是( )
A.矩形 B.菱形 C.正方形 D.梯形
8.如图,四边形ABCD中,AD∥BC,∠C=90°,AB=AD,连接BD,∠BAD的角平分线交BD、BC分别于点O、E,若EC=3,CD=4,则BO的长为( )
A.4 B.3 C.2 D.3
9.如图,两张等宽的纸条交叉重叠在一起,重叠的部分为四边形ABCD,若测得点A,C之间的距离为6cm,点B,D之间的距离为8cm,则纸条的宽为( )
A.5cm B.4.8cm C.4.6cm D.4cm
10.如图,在平行四边形中,用直尺和圆规作的平分线交于点E;以点A为圆心,的长为半径画弧交于点F.若,则的长为( )
A.16 B.15 C.14 D.13
11.如图,矩形的对角线,相交于点O,.若,则四边形的周长为( ).
A.4 B.6 C.8 D.10
12.如图,矩形的对角线,相交于点,点是的中点,连接并延长至,使,连接,,若,则四边形的周长为( )
A.8 B.4 C.16 D.6
13.如图,在矩形ABCD中,E、F、G、H分别为边AB、BC、CD、DA的中点.若AB=4,AD=6,则图中阴影部分的面积为( )
A.12 B.6 C.24 D.3
14.如图,四边形ABCD的对角线相交于点O,且点O是BD的中点.若,,,则四边形ABCD的面积为( )
A.48 B.24 C.20 D.15
15.如图,在矩形ABCD中,AB=5,AD=12,对角线BD的垂直平分线分别与AD,BC边交于点E、F,则四边形BFDE的面积为( )
A. B. C. D.
二、填空题
16.△ABC中,延长BA至D使得AB=AD,延长CA至E使得AC=AE,当△ABC满足条件________时,四边形BCDE是菱形.
17.如图,在菱形中,,,,分别为菱形四条边的中点,连接与,交于点,则图中的菱形共有________个.
18.如图,,,,,那么____时,四边形是菱形.
19.有两个全等矩形纸条,长与宽分别为10和6,按如图所示的方式交叉叠放在一起,则重合部分构成的四边形BGDH的周长为___.
20.如图,在△ABC中,AB=8,BC=10,点D为BC边的中点,点E是AB边上一点,连接ED,将△EDB沿DE翻折,得到△DEP,连接PC,PB,PA,若DP经过AC的中点F,且PC=2,则△AFP的面积是 _____.
三、解答题
21.如图,在 ABCD中,点O是对角线BD的中点,过点O作EF⊥BD,垂足为点O,且交AD,BC分别于点E,F.
求证:四边形BEDF是菱形.
22.如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,BD是对角线,过A点作交CB的延长线于点G.
(1)求证:.
(2)若,求证:四边形DEBF是菱形.
23.如图,在四边形ABCD中,,,对角线AC、BD交于点O,AC平分∠BAD,过点C作交AB的延长线于点E.
(1)求证:四边形ABCD是菱形;
(2)若,,求CE的长.
24.如图,在平行四边形ABCD中,AE⊥BC于点E,AF⊥CD于点F,AE、AF分别交BD于点G、H.AG=AH.
(1)如图1,求证:平行四边形ABCD是菱形;
(2)如图2,当∠ABC=60°时,连接CH,在不添加任何辅助线的情况下,请直接写出图2中面积等于△BEG面积2倍的所有三角形.
25.如图,四边形ABCD中,AB=AD,∠B=∠D,AE⊥BC于E,AF⊥CD于F,连接EF.
(1)求证:△AEF是等腰三角形;
(2)若,求证:四边形ABCD为菱形.
26.两个不全等的直角三角形ABC和DEF重叠在一起,其中∠A=60°,AC=1.固定△ABC不动,将△DEF进行如下操作:
(1)如图(1),△DEF沿线段AB向右平移(D点在线段AB内移动),连接DC、CF、FB,四边形的形状在不断的变化,但它的面积不变化,请求出其面积;
(2)如图(2),当点移到的中点时,请你猜想四边形的形状,并说明理由.
试卷第1页,共3页
参考答案:
1.B
解:略
2.B
解:A、错误,对角线相等的平行四边形是矩形;
B、 正确,根据矩形的性质:矩形的对角线相等且互相平分;
C、错误,对角线互相垂直的平行四边形是菱形;
D、错误,一组对边相等,另一组对边平行的四边形可能是等腰梯形、平行四边形、矩形、菱形、正方形.
故选:B.
3.A
解:① ABCD中,AC⊥BD,根据对角线互相垂直的平行四边形是菱形,即可判定 ABCD是菱形;故①正确;
② ABCD中,∠BAD=90°,根据有一个角是直角的平行四边形是矩形,即可判定 ABCD是矩形,而不能判定 ABCD是菱形;故②错误;
③ ABCD中,AB=BC,根据一组邻边相等的平行四边形是菱形,即可判定 ABCD是菱形;故③正确;
④ ABCD中,AC=BD,根据对角线相等的平行四边形是矩形,即可判定 ABCD是矩形,而不能判定 ABCD是菱形;故④错误.
故正确的为①③
故选:A.
4.B
解:如图,四边形ABCD是平行四边形
(1)四边形ABCD是平行四边形,AB=AD
平行四边形ABCD是菱形;
(2)四边形ABCD是平行四边形,AC=BD
平行四边形ABCD是矩形;
(3) ∠BOC=90°
四边形ABCD是平行四边形
平行四边形ABCD是菱形;
(4)四边形ABCD是平行四边形
∠ABC=∠BCD
平行四边形ABCD是矩形;
(5)四边形ABCD是平行四边形
∠ADB=∠CDB
即
平行四边形ABCD是菱形.
其中,能判定四边形ABCD是菱形的方法有3种
故选:B.
5.A
解:①,对角线相等的平行四边形是矩形,故①符合题意;
②,对角线垂直的平行四边形是菱形,故②不符合题意;
③,邻边相等的平行四边形是菱形,故③不符合题意;
④,
∵,
∴,
∴,
∴,邻边相等的平行四边形是菱形,故④不符合题意;
故选:A.
6.C
解:∵
∴四边形是平行四边形
∴,
∵平分
∴
∴
∴平行四边形AEDF是菱形
∴
故选C.
7.B
解:
展得到的图形如上图,
由操作过程可知:AB=CD,BC=AD,
∴四边形ABCD是平行四边形,
∵AC⊥BD,
∴四边形ABCD为菱形,
故选:B.
8.C
解:连接DE.
在直角三角形CDE中,EC=3,CD=4,根据勾股定理,得DE=5.
∵AB=AD, AE平分
∴AE⊥BD,BO=OD,
∴AE垂直平分BD,∠BAE=∠DAE.
∴DE=BE=5.
∵AD∥BC,
∴∠DAE=∠AEB,
∴∠BAE=∠AEB,
∴AB=BE=5,
∴BC=BE+EC=8,
∴四边形ABED是菱形,
由勾股定理得出,
∴,
故选:C.
9.B
解:作AR⊥BC于R,AS⊥CD于S,连接AC、BD交于点O.
由题意知:AD∥BC,AB∥CD,
∴四边形ABCD是平行四边形,
∵两个矩形等宽,
∴AR=AS,
∵AR BC=AS CD,
∴BC=CD,
∴平行四边形ABCD是菱形,
∴AC⊥BD,
在Rt△AOB中,
∵OA=3cm,OB=4cm,
∴AB==5cm,
∵平行四边形ABCD是菱形,
∴AB=BC=5cm,
∴菱形ABCD的面积,即,
解得: cm.
故选:B.
10.A
解:如图,连接,设交于点,
平分
四边形是平行四边形
,
又
四边形是平行四边形
四边形是菱形
,
在中,,
故选A
11.C
解:,,
四边形是平行四边形,
四边形是矩形,,
,,,
,
四边形是菱形,
,
四边形的周长,
故选:C.
12.B
解:∵矩形的对角线,相交于点,
∴,
∴OC=OD=1,
∴△OCD是等腰三角形,
∵点是的中点,
∴OM是△OCD的中线,也是高,
∴OM⊥CD,DM=CM,
∵,
∴四边形OCED中,对角线OE与CD互相垂直且平分,
∴四边形OCED菱形,
∴四边形的周长为:;
故选:B.
13.A
解:连接AC,BD,FH,EG,
∵E,F,G,H分别为边AB,BC,CD,DA的中点,
∴AH=AD,BF=BC,
∵四边形ABCD是矩形,
∴AD=BC,ADBC,
∴AH=BF,AHBF,
∴四边形AHFB是平行四边形,
∴FH=AB=2,
同理EG=AD=4,
∵四边形ABCD是矩形,
∴AC=BD,
∵E,F,G,H分别为边AB,BC,CD,DA的中点,
∴HGAC,HG=AC,EFAC,EF=AC,EH=BD,
∴EH=HG,GH=EF,GHEF,
∴四边形EFGH是平行四边形,
∴平行四边形EFGH是菱形,
∴FH⊥EG,
∴阴影部分EFGH的面积是×HF×EG=×6×4=12,
故选:A.
14.B
解:∵AB=AD,点O是BD的中点,
∴AC⊥BD,∠BAO=∠DAO,
∵∠ABD=∠CDB,
∴AB∥CD,
∴∠BAC=∠ACD,
∴∠DAC=∠ACD,
∴AD=CD,
∴AB=CD,
∴四边形ABCD是菱形,
∵AB=5,BO=BD=4,
∴AO=3,
∴AC=2AO=6,
∴四边形ABCD的面积=×6×8=24,
故选:B.
15.A
解:∵四边形ABCD是矩形,
∴AD∥BC,
∴∠DEO=∠BFO,∠EDO=∠FBO,
∵对角线BD的垂直平分线分别与AD,BC边交于点E、F,
∴BO=DO,EF⊥BD,
∴△DEO≌△BFO(AAS),
∴EO=FO,
∵BO=DO,
∴四边形BEDF是平行四边形,
∵EF⊥BD,
∴平行四边形BEDF是菱形,
∴BE=DE,
∵AB=5,AD=12,∠A=90°,
∴BD=13,
设DE=x,则AE=12﹣x,
在Rt△AEB中,AB2+AE2=BE2,
即52+(12﹣x)2=x2,
∴x,
∴BE=DE,
在Rt△BEO中,OE,
∴EF=2EO,
∴菱形BEDF的面积,
故选:A.
16.∠BAC=90°
解:如图所示:∵AB=AD,EA=AC,
∴四边形EBCD是平行四边形;
当BD⊥EC时,四边形BCDE是菱形,
此时∠BAC=90°.
故答案为:∠BAC=90°.
17.5
解:∵四边形ABCD是菱形,E,F,F,H分别是菱形四边的中点,
∴AE=AH=HD=GD=CG=CF=FB=BE=OE=OG=OH=OF,
∴四边形AEOH,HOGD,EOFB,OFGC和ABCD均为菱形,共5个.
故答案为:5.
18.
解:当时,四边形是菱形,
证明:∵AD∥BC,AB∥CD,
∴四边形是平行四边形,
∵,
∴∠ADB=30°,
∵,
∴∠ABD=30°=∠ADB,
∴AB=AD,
∴四边形是菱形,
故答案为:.
19.##27.2
解:由题意得:矩形ABCD≌矩形BEDF,
∴∠A=90°,AB=BE=6,AD∥BC,BF∥DE,AD=10,
∴四边形BGDH是平行四边形,
∴平行四边形BGDH的面积=BG×AB=BH×BE,
∴BG=BH,
∴四边形BGDH是菱形,
∴BH=DH=DG=BG,
设BH=DH=x,则AH=10-x,
在Rt△ABH中,由勾股定理得:62+(10-x)2=x2,
解得:x=,
∴BH=,
∴四边形BGDH的周长=4BH=.
故答案为:
20.##
解:过点D作 DM⊥AB于点M,设ED与BP交于点O,
∵点D是BC边的中点,点F是AC的中点,
∴DP∥BE,
∴∠EBD=∠PDC,
又∵∠EPD=∠EBD,
∴∠EPD=∠PDC,
∴EP∥BD,
∴四边形BDPE为平行四边形,
又∵BD=DP,
∴平行四边形BDPE为菱形,
∴EP=BD=BE=DP=CD=5,BP⊥ED,
∴四边形 EPCD为平行四边形,
∴ED=PC=2,ED∥CP,
∵DP∥BE,即DP∥EG,
∴四边形EDPG是平行四边形,
∴EG=DP=5,PG=ED=2,
∴PG=CP,
∴PF是△ACG中位线,
∵AE=AB﹣BE=8﹣5=3,
∴AG=EG﹣AE=5﹣3=2,
∴PFAG=1,
在 Rt△BOE中,
BE=BD=5,EODE=1,
∴BO2,
∴S△BDEDE BO=2BE DM,
∴DM,
∵平行线间的距离相等,△AFP以PF为底,高即为,
∴S△AFPPF1,
故答案为:.
21.证明见解析
解:∵四边形ABCD是平行四边形,O为对角线BD的中点,
∴BO=DO,AD∥BC,
∴∠EDB=∠FBO,
在△EOD和△FOB中,,
∴△DOE≌△BOF(ASA);
∴OE=OF,
又∵OB=OD,
∴四边形BEDF是平行四边形,
∵EF⊥BD,
∴平行四边形BEDF为菱形.
22.(1)见解析 (2)见解析
(1)
∵四边形ABCD是平行四边形,
∴,,,
∵E、F分别为边AB、CD的中点,
∴,.
∴四边形DEBF是平行四边形,
∴.
(2)
∵,,
∴.
又∵F分别为边CD的中点,
∴.
∴平行四边形DEBF是菱形.
23.(1)见解析; (2)
(1)
证明:∵,
∴,
∵AC平分∠BAD,
∴,
∴,
∴,
∵AB=AD,
∴,
∵,
∴四边形ABCD是平行四边形,
又∵,
∴四边形ABCD是菱形;
(2)
∵四边形ABCD是菱形,BD=6,AC=8,
∴,,,
∴,
在中,根据勾股定理可知,
,
∴菱形的面积,
∵,
∴菱形面积,
∴.
24.(1)见解析;
(2)面积等于△BEG面积2倍的所有三角形有:△ABG,△ADH,△AGH,△DHC
(1)
证明:∵AG=AH,
∴∠AGH=∠AHG,
∵∠AGH=∠BGE,∠DHF=∠AHG,
∴∠BGE=∠DHF,
∵AE⊥BC,AF⊥CD,
∴∠BEG=∠DFH,
∴∠EBG=∠FDH,
∴∠CBD=∠CDB,
∴BC=CD,
∵四边形ABCD是平行四边形,
∴平行四边形ABCD是菱形;
(2)
解:面积等于△BEG面积2倍的三角形有:△ABG,△ADH,△AGH,△DHC,
∵四边形ABCD是菱形,∠ABC=60°,AE⊥BC,AF⊥CD,
∴∠DBC=∠ABD=∠BAE=∠DAF=30°,
设GE=a,
∴BG=2a,BE=a,
∵∠ABG=∠BAG=30°,
∴AG=BG=2a,
∴S△ABG=2S△BEG;
在△ABG和△ADH中,
,
∴△ABG≌△ADH(SAS),
同理△CDH≌△ADH(SAS),
∴△ABG≌△ADH≌△CDH,
∴S△ABG=S△ADH=S△CDH=2S△BEG;
∵∠GAH=120°-30°-30°=60°,AG=AH,
∴△AGH是等边三角形,
∴GH=AG=BG,
∴S△AGH=S△ABG=2S△BEG;
综上所述:面积等于△BEG面积2倍的所有三角形有:△ABG,△ADH,△AGH,△DHC.
25.(1)见解析 (2)见解析
(1)
证明:∵AE⊥BC,AF⊥CD,
∴∠AEB=∠AFD=90°,
在△ABE和△ADF中,
,
∴△ABE≌△ADF(AAS),
∴AE=AF,
∴△AEF是等腰三角形;
(2)
∵,
∴∠B+∠C=180°,
∵∠B=∠D,
∴∠D+∠C=180°,
∴,
∴四边形ABCD为平行四边形,
又∵AB=AD,
∴平行四边形ABCD为菱形.
26.(1) (2)四边形是菱形,理由见解析
(1)
解:过点作,垂足是点.
由题可知,,,
则四边形是梯形.
在直角中,,,,
,
在直角中,,,,
,,
.
;
(2)
证明:四边形是菱形.
理由如下:在直角中,是的中点,
,
由(1),
,
又,
四边形是平行四边形.
,
四边形是菱形.
答案第1页,共2页
