8.3动能和动能定理(Word版含答案)
文档属性
| 名称 | 8.3动能和动能定理(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 459.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-03-20 00:00:00 | ||
图片预览



文档简介
8.3 动能和动能定理
一、单选题
1.某同学参加学校运动会立定跳远项目比赛,起跳直至着地过程如图,测量得到比赛成绩是2.5m,目测空中脚离地最大高度约0.8m,忽略空气阻力,则起跳过程该同学所做功约为( )
A.65J B.350J
C.700J D.1550J
2.如图所示,电梯轿厢质量为M,底板上放置一个质量为m的物体,钢索拉着轿厢由静止开始向上加速运动,当上升高度为H时,速度达到v,不计空气阻力,则在此过程中( )
A.钢索的拉力做功等于
B.钢索对轿厢及物体构成的系统做功等于
C.底板支持力对物体做功等于
D.物体克服重力做功的平均功率等于mgv
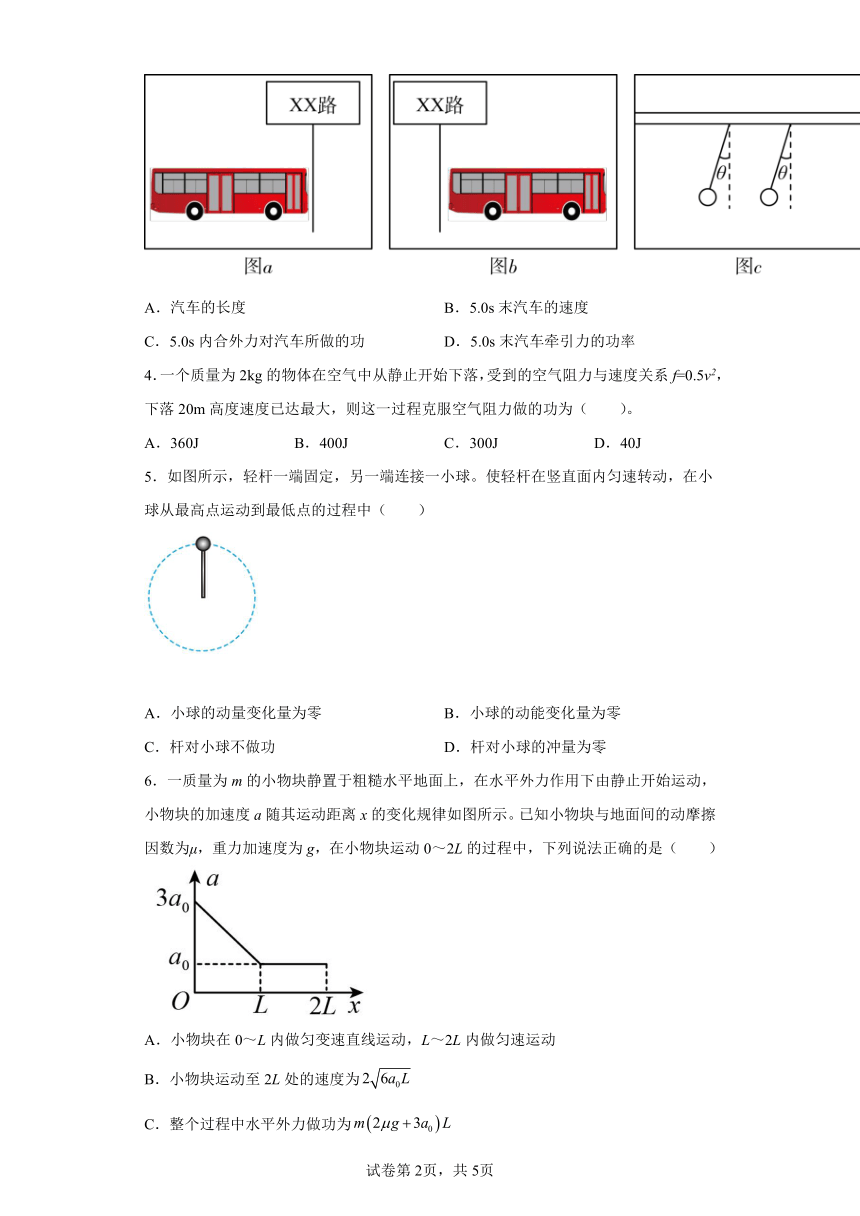
3.图中a、b所示是一辆质量为6.0×103kg的公共汽车在t=0和t=5.0s末两个时刻的两张照片。当t=0时,汽车刚启动(汽车的运动可看成匀加速直线运动)。图c是车内横杆上悬挂的拉手环经放大后的图像,约为30°。根据题中提供的信息,不能估算出的物理量有( )
A.汽车的长度 B.5.0s末汽车的速度
C.5.0s内合外力对汽车所做的功 D.5.0s末汽车牵引力的功率
4.一个质量为2kg的物体在空气中从静止开始下落,受到的空气阻力与速度关系f=0.5v2,下落20m高度速度已达最大,则这一过程克服空气阻力做的功为( )。
A.360J B.400J C.300J D.40J
5.如图所示,轻杆一端固定,另一端连接一小球。使轻杆在竖直面内匀速转动,在小球从最高点运动到最低点的过程中( )
A.小球的动量变化量为零 B.小球的动能变化量为零
C.杆对小球不做功 D.杆对小球的冲量为零
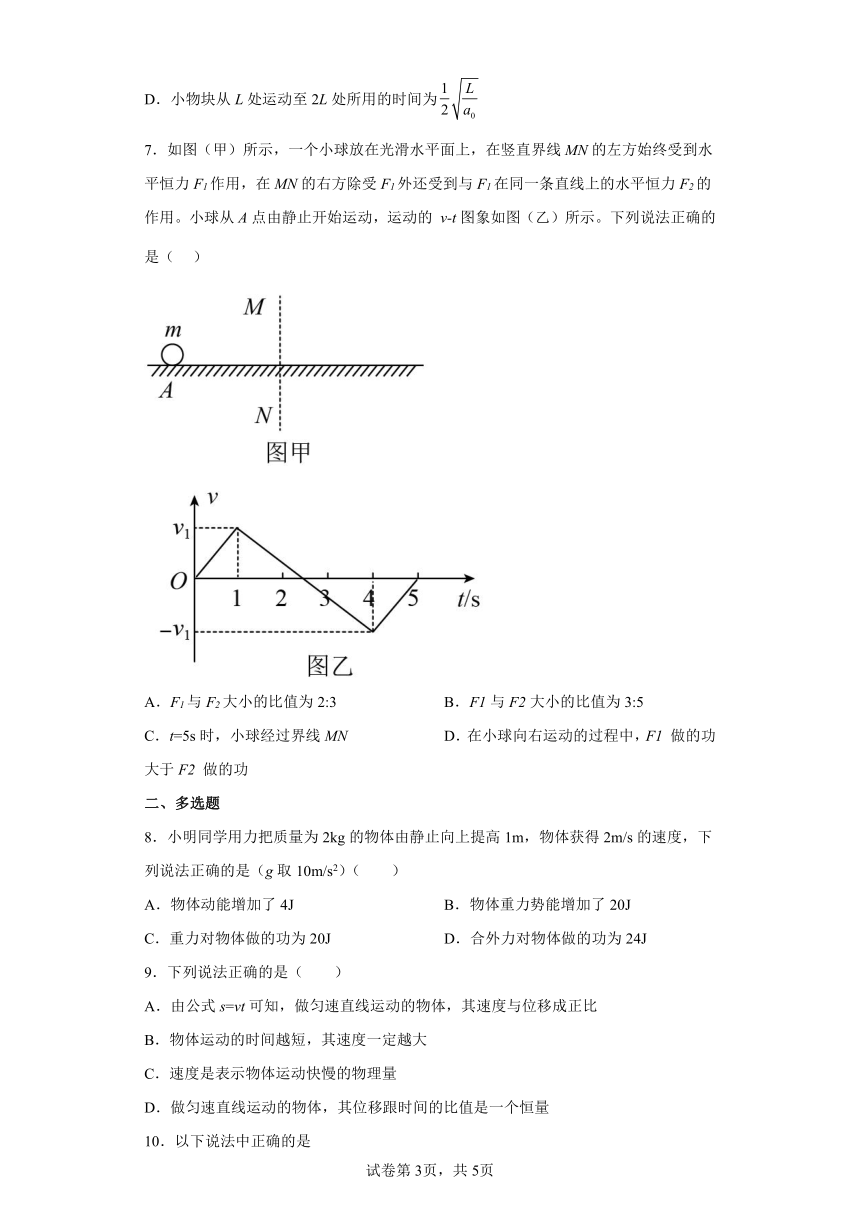
6.一质量为m的小物块静置于粗糙水平地面上,在水平外力作用下由静止开始运动,小物块的加速度a随其运动距离x的变化规律如图所示。已知小物块与地面间的动摩擦因数为μ,重力加速度为g,在小物块运动0~2L的过程中,下列说法正确的是( )
A.小物块在0~L内做匀变速直线运动,L~2L内做匀速运动
B.小物块运动至2L处的速度为
C.整个过程中水平外力做功为
D.小物块从L处运动至2L处所用的时间为
7.如图(甲)所示,一个小球放在光滑水平面上,在竖直界线MN的左方始终受到水平恒力F1作用,在MN的右方除受F1外还受到与F1在同一条直线上的水平恒力F2的作用。小球从A点由静止开始运动,运动的 v-t图象如图(乙)所示。下列说法正确的是( )
A.F1与F2大小的比值为2:3 B.F1与F2大小的比值为3:5
C.t=5s时,小球经过界线MN D.在小球向右运动的过程中,F1 做的功大于F2 做的功
二、多选题
8.小明同学用力把质量为2kg的物体由静止向上提高1m,物体获得2m/s的速度,下列说法正确的是(g取10m/s2)( )
A.物体动能增加了4J B.物体重力势能增加了20J
C.重力对物体做的功为20J D.合外力对物体做的功为24J
9.下列说法正确的是( )
A.由公式s=vt可知,做匀速直线运动的物体,其速度与位移成正比
B.物体运动的时间越短,其速度一定越大
C.速度是表示物体运动快慢的物理量
D.做匀速直线运动的物体,其位移跟时间的比值是一个恒量
10.以下说法中正确的是
A.是决定式;是定义式
B.是定义式;是决定式
C.两个力的合成是唯一的,两个力的分解是任意的
D.两个力的合成是任意的,两个力的分解是唯一的
11.我国计划于2020年前后实施的火星探测进展顺利,探测任务中将完成对火星的环绕和着陆巡视探索,收集火星的空间环境、形貌特征、表层结构、大气环境等重要数据。若探测器的质量为m,在火星表面上受到的重力为P,火星的半径为R,则探测器在距火星表面高度为h的圆形轨道上做匀速圆周运动时( )
A.线速度大小为 B.周期为
C.所受火星引力大小为 D.动能为
三、解答题
12.如图甲所示,长为4m的水平轨道AB与半径为R=0.8m的竖直半圆弧轨道BC在B处相连接。有一质量为1kg的滑块(大小不计)受水平向右的力F的作用,从A处以3m/s的初速度开始向右运动,F的大小随位移变化的关系如图乙所示。滑块与AB间的动摩擦因数μ=0.25,与BC间的动摩擦因数未知,g取,求:
(1)滑块到达B处时的速度大小;
(2)若到达B点时撤去力F,滑块沿半圆弧轨道内侧上滑,到达最高点C时,滑块对轨道的压力恰好等于滑块的重力,则滑块在半圆弧轨道上克服摩擦力所做的功是多少?
13.如图是越野滑雪障碍追逐赛一段简化的赛道。某次比赛中,质量m=60kg的运动员从 A点滑下,经过AC段赛道最低点B点时速度为20m/s,经过BD段赛道最高点C点时的速度为10m/s,已知B、C两点的曲率圆半径分别为R1=10.0m,R2=16.0m,A、B两点的高度差为A=30.0m,取g=lOm/s2。求:(赛道在同一竖直平面内)
(1)从A到B阻力对运动员做的功;
(2)运动员经过B点和C点时受到雪道的弹力
14.如图所示,在竖直平面内有一条 圆弧形轨道AB,其半径为1m,B点的切线方向恰好为水平方向.一个质量为2kg的小物体,从轨道顶端A点由静止开始沿轨道下滑,到达轨道末端B点时的速度为4m/s,然后做平抛运动,落到地面上的C点.若轨道距地面的高度h为5m(不计空气阻力,g=10m/s2),求:
(1)物体在AB轨道克服阻力做的功;
(2)物体在B点对轨道的压力;
(3)物体落地时的动能;
(4)B、C两点间的水平距离.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【解析】
【分析】
【详解】
运动员做抛体运动,从起跳到达到最大高度的过程中,竖直方向做加速度为g的匀减速直线运动,则
竖直方向初速度
vy=gt=4m/s
水平方向做匀速直线运动,则
则起跳时的速度
设中学生的质量为60kg,根据动能定理得:
最接近的是C选项。
故选C。
2.C
【解析】
【分析】
对电梯和物体整体运用动能定理求解拉力做功.对物体运用动能定理求解支持力做功.平均功率根据公式求解.
【详解】
对系统,由动能定理得,解得钢索的拉力的功,AB错误;对物体,由动能定理得,解得到地板对物体的支持力做的功为,C正确;地板克服物体的重力做功的平均功率,D错误.
【点睛】
应用动能定理应注意的几个问题(1)明确研究对象和研究过程,找出始末状态的速度.(2)要对物体正确地进行受力分析,明确各力做功的大小及正负情况(待求的功除外).(3)有些力在物体运动过程中不是始终存在的.若物体运动过程中包括几个阶段,物体在不同阶段内的受力情况不同,在考虑外力做功时需根据情况区分对待.
3.D
【解析】
【分析】
【详解】
A.根据牛顿第二定律悬挂的拉手环可知加速度为
则汽车的长度可用
L=
求得,故A不符合题意;
B.5s末汽车的速度可用
v=at
求得,故B不符合题意;
C.5s内合外力对汽车所做的功
W=
可求,故C不符合题意;
D.因为牵引力未知所以无法求得5s末汽车牵引力的功率,故D符合题意。
故选D。
4.A
【解析】
【分析】
【详解】
由题意可知
由动能定理可得
解得
故选A。
5.B
【解析】
【详解】
AD.设小球在竖直面内以v匀速转动,小球从最高点运动到最低点的过程中,速度大小不变,方向相反,以最低点速度方向为正方向,故小球的动量变化量为
由动量定理可知,杆对小球的冲量不为零,AD错误;
B.小球速度大小不变,动能不变,故小球的动能变化量为零,B正确。
C.小球从最高点运动到最低点的过程中,由动能定理可得
解得
故杆对小球做负功,C错误。
故选B。
6.C
【解析】
【详解】
A.小物块在0~L内加速度减小,做加速度减小的变加速直线运动,L~2L内加速度不变,做匀加速运动,故A错误;
B.整个过程,根据动能定理得:
,
得小物块运动至2L处的速度为:
,
故B错误;
C.整个过程,根据动能定理得:
,
联立解得水平外力做功为
,
故C正确;
D.设小物块运动至L处的速度为.根据动能定理得:
,
得
,
小物块从L处运动至2L处做匀加速直线运动,有
,
联立解得
,
故D错误。
故选:C。
7.B
【解析】
【分析】
【详解】
AB.由图乙可得,取向右为正方向,小球在1s前做匀加速运动,所以它对应于图甲中MN左侧,且F1水平向右,在1s到4s小球先做匀减速运动,后做反向匀加速运动,它对应于图甲MN右侧小球的运动,可知F2方向水平向左。且根据牛顿第二定律
且根据图像可知
即
可求
A错误,B正确;
C.5s时,小球位移为零,回到出发点,C错误;
D.由图像乙可知,小球0-2.5s向右运动,且2.5s时小球速度为零,由以上分析知,F1水平向右做正功,F2水平向左做负功,由动能定理可知0-2.5s过程合外力做功为零,即F1,F2做功大小相等,D错误。
故选B。
8.AB
【解析】
【详解】
A.物体的初动能为0,末速度为v=2m/s,则物体动能增加量为
故A正确;
BC.重力对物体做的功为
由功能关系可知,物体重力势能增加量为20J,故B正确,C错误;
D.根据动能定理知,合外力做功等于动能的变化,即
故D错误。
故选AB。
9.CD
【解析】
【详解】
A.速度取决于位移与时间的比值,与位移大小没关系,故A错误;
B.物体运动的时间短,但如果位移很小,则速度不一定大,故B错误;
C.速度是描述物体运动快慢的物理量,故C正确;
D.做匀速直线运动的物体,速度保持不变,则其位移与时间的比值是一个恒量,故D正确。
故选CD。
10.BC
【解析】
【详解】
AB.加速度
是定义式,根据牛顿第二定律可知加速度与物体所受合力成正比,与物体的质量成反比,即是加速度的决定式,故A错误,B正确;
CD.两个力的合成,根据力的平行四边形定则,相当于已知平行四边形的两个邻边求对角线,所以两个力合成时其合力是一定的,唯一的;如果不加限制条件的话,一个力可以分解成无数对分力,故C正确,D错误。
11.AC
【解析】
【分析】
【详解】
探测器绕火星做匀速圆周运动,由万有引力提供向心力可得
探测器在火星表面上受到的引力等于重力
联立解得线速度大小为
周期为
所受火星引力大小为
探测器的动能为
故选AC。
12.(1)7 m/s;(2)0.5 J
【解析】
【详解】
(1)设B点的速度为vB,滑块从A到B的过程,由动能定理得
代入数据解得
(2)当滑块恰好能到达最高点C时,有
由于滑块对轨道的压力恰好等于滑块的重力,根据牛顿第三定律有
设摩擦力做功为Wf,对滑块从B到C的过程,由动能定理得
联立上式,代入数据解得
即滑块克服摩擦力做的功为0.5 J。
13.(1)-6000J;(2)225N
【解析】
【分析】
【详解】
(1)运动员从A到B的运动过程只有重力、阻力做功,由动能定理可得
(2)运动员在B点时,在竖直方向上应用牛顿第二定律可得
运动员在C点时,在竖直方向上应用牛顿第二定律可得
14.(1)4J;(2)52N;(3)116J;(4)4m
【解析】
【分析】
【详解】
(1)设小滑块在AB轨道上克服阻力做功为W,对于从A至B过程,根据动能定理得
代入数据解得
(2)物体在B点受到的支持力和重力的合力提供向心力
所以
根据牛顿第三定律,物体在B点受到的支持力和物体在B点对轨道的压力大小相等,方向相反,所以物体在B点对轨道的压力大小也是52 N
(3)设小滑块落地时的动能为Ek,取地面为零重力势能参照考面,由于平抛过程中只有重力做功,故根据机械能守恒定律得
代入数据解得
(4)小球离开B之后做平抛运动
B、C两点间的水平距离等于小球平抛的水平距离
答案第1页,共2页
答案第1页,共2页
一、单选题
1.某同学参加学校运动会立定跳远项目比赛,起跳直至着地过程如图,测量得到比赛成绩是2.5m,目测空中脚离地最大高度约0.8m,忽略空气阻力,则起跳过程该同学所做功约为( )
A.65J B.350J
C.700J D.1550J
2.如图所示,电梯轿厢质量为M,底板上放置一个质量为m的物体,钢索拉着轿厢由静止开始向上加速运动,当上升高度为H时,速度达到v,不计空气阻力,则在此过程中( )
A.钢索的拉力做功等于
B.钢索对轿厢及物体构成的系统做功等于
C.底板支持力对物体做功等于
D.物体克服重力做功的平均功率等于mgv
3.图中a、b所示是一辆质量为6.0×103kg的公共汽车在t=0和t=5.0s末两个时刻的两张照片。当t=0时,汽车刚启动(汽车的运动可看成匀加速直线运动)。图c是车内横杆上悬挂的拉手环经放大后的图像,约为30°。根据题中提供的信息,不能估算出的物理量有( )
A.汽车的长度 B.5.0s末汽车的速度
C.5.0s内合外力对汽车所做的功 D.5.0s末汽车牵引力的功率
4.一个质量为2kg的物体在空气中从静止开始下落,受到的空气阻力与速度关系f=0.5v2,下落20m高度速度已达最大,则这一过程克服空气阻力做的功为( )。
A.360J B.400J C.300J D.40J
5.如图所示,轻杆一端固定,另一端连接一小球。使轻杆在竖直面内匀速转动,在小球从最高点运动到最低点的过程中( )
A.小球的动量变化量为零 B.小球的动能变化量为零
C.杆对小球不做功 D.杆对小球的冲量为零
6.一质量为m的小物块静置于粗糙水平地面上,在水平外力作用下由静止开始运动,小物块的加速度a随其运动距离x的变化规律如图所示。已知小物块与地面间的动摩擦因数为μ,重力加速度为g,在小物块运动0~2L的过程中,下列说法正确的是( )
A.小物块在0~L内做匀变速直线运动,L~2L内做匀速运动
B.小物块运动至2L处的速度为
C.整个过程中水平外力做功为
D.小物块从L处运动至2L处所用的时间为
7.如图(甲)所示,一个小球放在光滑水平面上,在竖直界线MN的左方始终受到水平恒力F1作用,在MN的右方除受F1外还受到与F1在同一条直线上的水平恒力F2的作用。小球从A点由静止开始运动,运动的 v-t图象如图(乙)所示。下列说法正确的是( )
A.F1与F2大小的比值为2:3 B.F1与F2大小的比值为3:5
C.t=5s时,小球经过界线MN D.在小球向右运动的过程中,F1 做的功大于F2 做的功
二、多选题
8.小明同学用力把质量为2kg的物体由静止向上提高1m,物体获得2m/s的速度,下列说法正确的是(g取10m/s2)( )
A.物体动能增加了4J B.物体重力势能增加了20J
C.重力对物体做的功为20J D.合外力对物体做的功为24J
9.下列说法正确的是( )
A.由公式s=vt可知,做匀速直线运动的物体,其速度与位移成正比
B.物体运动的时间越短,其速度一定越大
C.速度是表示物体运动快慢的物理量
D.做匀速直线运动的物体,其位移跟时间的比值是一个恒量
10.以下说法中正确的是
A.是决定式;是定义式
B.是定义式;是决定式
C.两个力的合成是唯一的,两个力的分解是任意的
D.两个力的合成是任意的,两个力的分解是唯一的
11.我国计划于2020年前后实施的火星探测进展顺利,探测任务中将完成对火星的环绕和着陆巡视探索,收集火星的空间环境、形貌特征、表层结构、大气环境等重要数据。若探测器的质量为m,在火星表面上受到的重力为P,火星的半径为R,则探测器在距火星表面高度为h的圆形轨道上做匀速圆周运动时( )
A.线速度大小为 B.周期为
C.所受火星引力大小为 D.动能为
三、解答题
12.如图甲所示,长为4m的水平轨道AB与半径为R=0.8m的竖直半圆弧轨道BC在B处相连接。有一质量为1kg的滑块(大小不计)受水平向右的力F的作用,从A处以3m/s的初速度开始向右运动,F的大小随位移变化的关系如图乙所示。滑块与AB间的动摩擦因数μ=0.25,与BC间的动摩擦因数未知,g取,求:
(1)滑块到达B处时的速度大小;
(2)若到达B点时撤去力F,滑块沿半圆弧轨道内侧上滑,到达最高点C时,滑块对轨道的压力恰好等于滑块的重力,则滑块在半圆弧轨道上克服摩擦力所做的功是多少?
13.如图是越野滑雪障碍追逐赛一段简化的赛道。某次比赛中,质量m=60kg的运动员从 A点滑下,经过AC段赛道最低点B点时速度为20m/s,经过BD段赛道最高点C点时的速度为10m/s,已知B、C两点的曲率圆半径分别为R1=10.0m,R2=16.0m,A、B两点的高度差为A=30.0m,取g=lOm/s2。求:(赛道在同一竖直平面内)
(1)从A到B阻力对运动员做的功;
(2)运动员经过B点和C点时受到雪道的弹力
14.如图所示,在竖直平面内有一条 圆弧形轨道AB,其半径为1m,B点的切线方向恰好为水平方向.一个质量为2kg的小物体,从轨道顶端A点由静止开始沿轨道下滑,到达轨道末端B点时的速度为4m/s,然后做平抛运动,落到地面上的C点.若轨道距地面的高度h为5m(不计空气阻力,g=10m/s2),求:
(1)物体在AB轨道克服阻力做的功;
(2)物体在B点对轨道的压力;
(3)物体落地时的动能;
(4)B、C两点间的水平距离.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【解析】
【分析】
【详解】
运动员做抛体运动,从起跳到达到最大高度的过程中,竖直方向做加速度为g的匀减速直线运动,则
竖直方向初速度
vy=gt=4m/s
水平方向做匀速直线运动,则
则起跳时的速度
设中学生的质量为60kg,根据动能定理得:
最接近的是C选项。
故选C。
2.C
【解析】
【分析】
对电梯和物体整体运用动能定理求解拉力做功.对物体运用动能定理求解支持力做功.平均功率根据公式求解.
【详解】
对系统,由动能定理得,解得钢索的拉力的功,AB错误;对物体,由动能定理得,解得到地板对物体的支持力做的功为,C正确;地板克服物体的重力做功的平均功率,D错误.
【点睛】
应用动能定理应注意的几个问题(1)明确研究对象和研究过程,找出始末状态的速度.(2)要对物体正确地进行受力分析,明确各力做功的大小及正负情况(待求的功除外).(3)有些力在物体运动过程中不是始终存在的.若物体运动过程中包括几个阶段,物体在不同阶段内的受力情况不同,在考虑外力做功时需根据情况区分对待.
3.D
【解析】
【分析】
【详解】
A.根据牛顿第二定律悬挂的拉手环可知加速度为
则汽车的长度可用
L=
求得,故A不符合题意;
B.5s末汽车的速度可用
v=at
求得,故B不符合题意;
C.5s内合外力对汽车所做的功
W=
可求,故C不符合题意;
D.因为牵引力未知所以无法求得5s末汽车牵引力的功率,故D符合题意。
故选D。
4.A
【解析】
【分析】
【详解】
由题意可知
由动能定理可得
解得
故选A。
5.B
【解析】
【详解】
AD.设小球在竖直面内以v匀速转动,小球从最高点运动到最低点的过程中,速度大小不变,方向相反,以最低点速度方向为正方向,故小球的动量变化量为
由动量定理可知,杆对小球的冲量不为零,AD错误;
B.小球速度大小不变,动能不变,故小球的动能变化量为零,B正确。
C.小球从最高点运动到最低点的过程中,由动能定理可得
解得
故杆对小球做负功,C错误。
故选B。
6.C
【解析】
【详解】
A.小物块在0~L内加速度减小,做加速度减小的变加速直线运动,L~2L内加速度不变,做匀加速运动,故A错误;
B.整个过程,根据动能定理得:
,
得小物块运动至2L处的速度为:
,
故B错误;
C.整个过程,根据动能定理得:
,
联立解得水平外力做功为
,
故C正确;
D.设小物块运动至L处的速度为.根据动能定理得:
,
得
,
小物块从L处运动至2L处做匀加速直线运动,有
,
联立解得
,
故D错误。
故选:C。
7.B
【解析】
【分析】
【详解】
AB.由图乙可得,取向右为正方向,小球在1s前做匀加速运动,所以它对应于图甲中MN左侧,且F1水平向右,在1s到4s小球先做匀减速运动,后做反向匀加速运动,它对应于图甲MN右侧小球的运动,可知F2方向水平向左。且根据牛顿第二定律
且根据图像可知
即
可求
A错误,B正确;
C.5s时,小球位移为零,回到出发点,C错误;
D.由图像乙可知,小球0-2.5s向右运动,且2.5s时小球速度为零,由以上分析知,F1水平向右做正功,F2水平向左做负功,由动能定理可知0-2.5s过程合外力做功为零,即F1,F2做功大小相等,D错误。
故选B。
8.AB
【解析】
【详解】
A.物体的初动能为0,末速度为v=2m/s,则物体动能增加量为
故A正确;
BC.重力对物体做的功为
由功能关系可知,物体重力势能增加量为20J,故B正确,C错误;
D.根据动能定理知,合外力做功等于动能的变化,即
故D错误。
故选AB。
9.CD
【解析】
【详解】
A.速度取决于位移与时间的比值,与位移大小没关系,故A错误;
B.物体运动的时间短,但如果位移很小,则速度不一定大,故B错误;
C.速度是描述物体运动快慢的物理量,故C正确;
D.做匀速直线运动的物体,速度保持不变,则其位移与时间的比值是一个恒量,故D正确。
故选CD。
10.BC
【解析】
【详解】
AB.加速度
是定义式,根据牛顿第二定律可知加速度与物体所受合力成正比,与物体的质量成反比,即是加速度的决定式,故A错误,B正确;
CD.两个力的合成,根据力的平行四边形定则,相当于已知平行四边形的两个邻边求对角线,所以两个力合成时其合力是一定的,唯一的;如果不加限制条件的话,一个力可以分解成无数对分力,故C正确,D错误。
11.AC
【解析】
【分析】
【详解】
探测器绕火星做匀速圆周运动,由万有引力提供向心力可得
探测器在火星表面上受到的引力等于重力
联立解得线速度大小为
周期为
所受火星引力大小为
探测器的动能为
故选AC。
12.(1)7 m/s;(2)0.5 J
【解析】
【详解】
(1)设B点的速度为vB,滑块从A到B的过程,由动能定理得
代入数据解得
(2)当滑块恰好能到达最高点C时,有
由于滑块对轨道的压力恰好等于滑块的重力,根据牛顿第三定律有
设摩擦力做功为Wf,对滑块从B到C的过程,由动能定理得
联立上式,代入数据解得
即滑块克服摩擦力做的功为0.5 J。
13.(1)-6000J;(2)225N
【解析】
【分析】
【详解】
(1)运动员从A到B的运动过程只有重力、阻力做功,由动能定理可得
(2)运动员在B点时,在竖直方向上应用牛顿第二定律可得
运动员在C点时,在竖直方向上应用牛顿第二定律可得
14.(1)4J;(2)52N;(3)116J;(4)4m
【解析】
【分析】
【详解】
(1)设小滑块在AB轨道上克服阻力做功为W,对于从A至B过程,根据动能定理得
代入数据解得
(2)物体在B点受到的支持力和重力的合力提供向心力
所以
根据牛顿第三定律,物体在B点受到的支持力和物体在B点对轨道的压力大小相等,方向相反,所以物体在B点对轨道的压力大小也是52 N
(3)设小滑块落地时的动能为Ek,取地面为零重力势能参照考面,由于平抛过程中只有重力做功,故根据机械能守恒定律得
代入数据解得
(4)小球离开B之后做平抛运动
B、C两点间的水平距离等于小球平抛的水平距离
答案第1页,共2页
答案第1页,共2页
