2021-2022学年北师大版九年级数学下册第三章圆单元检测(Word版含答案)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学下册第三章圆单元检测(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 338.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-21 12:08:13 | ||
图片预览

文档简介
圆单元检测
一、单选题
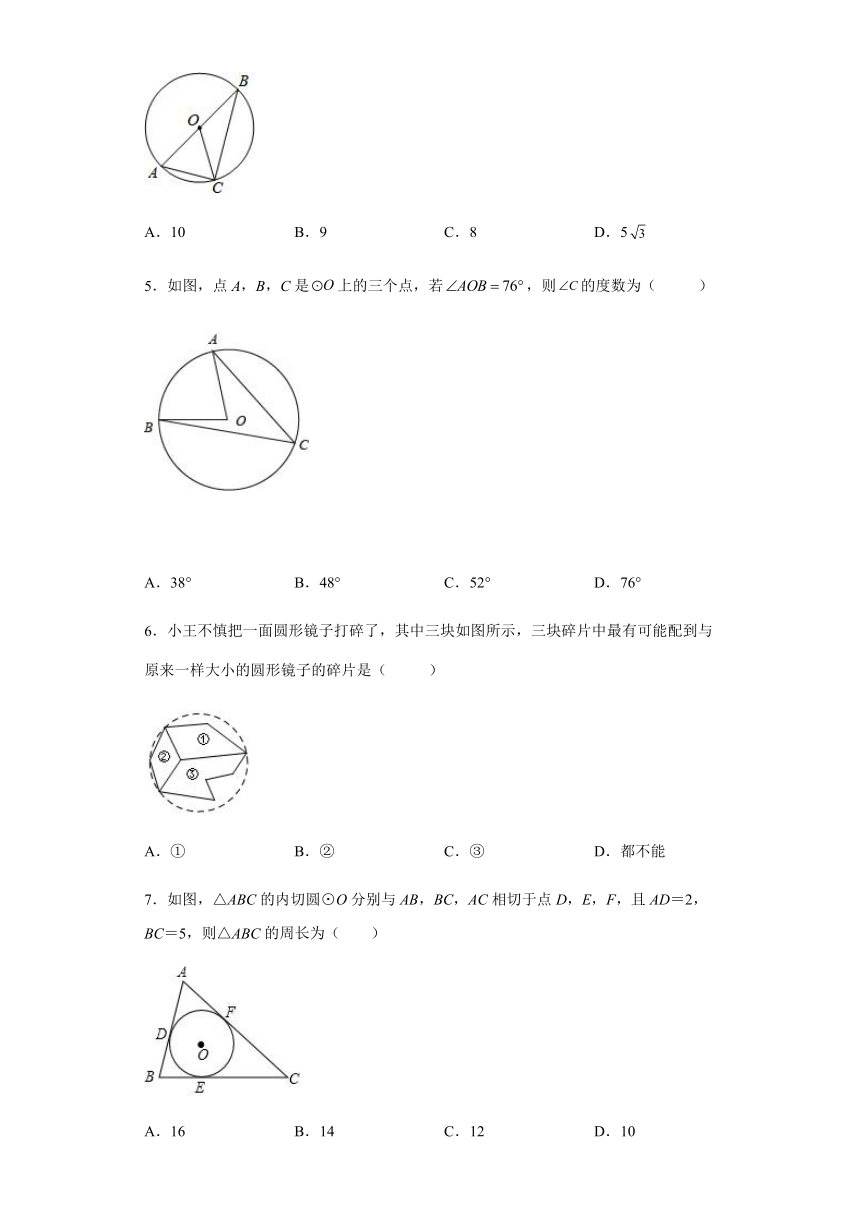
1.下列说法中,正确的是( )
A.相等的圆心角所对的弧相等
B.过任意三点可以画一个圆
C.周长相等的圆是等圆
D.平分弦的直径垂直于弦
2.如图,CD为的直径,弦于点E,,,则直径CD的长是( )
A.4 B.8 C.26 D.10
3.如图在平面直角坐标系中,过格点A,B,C作一圆弧,圆心坐标是( )
A. B. C. D.
4.如图,⊙O为△ABC的外接圆,且AB为⊙O的直径,若OC=AC=5,则BC长为( )
A.10 B.9 C.8 D.5
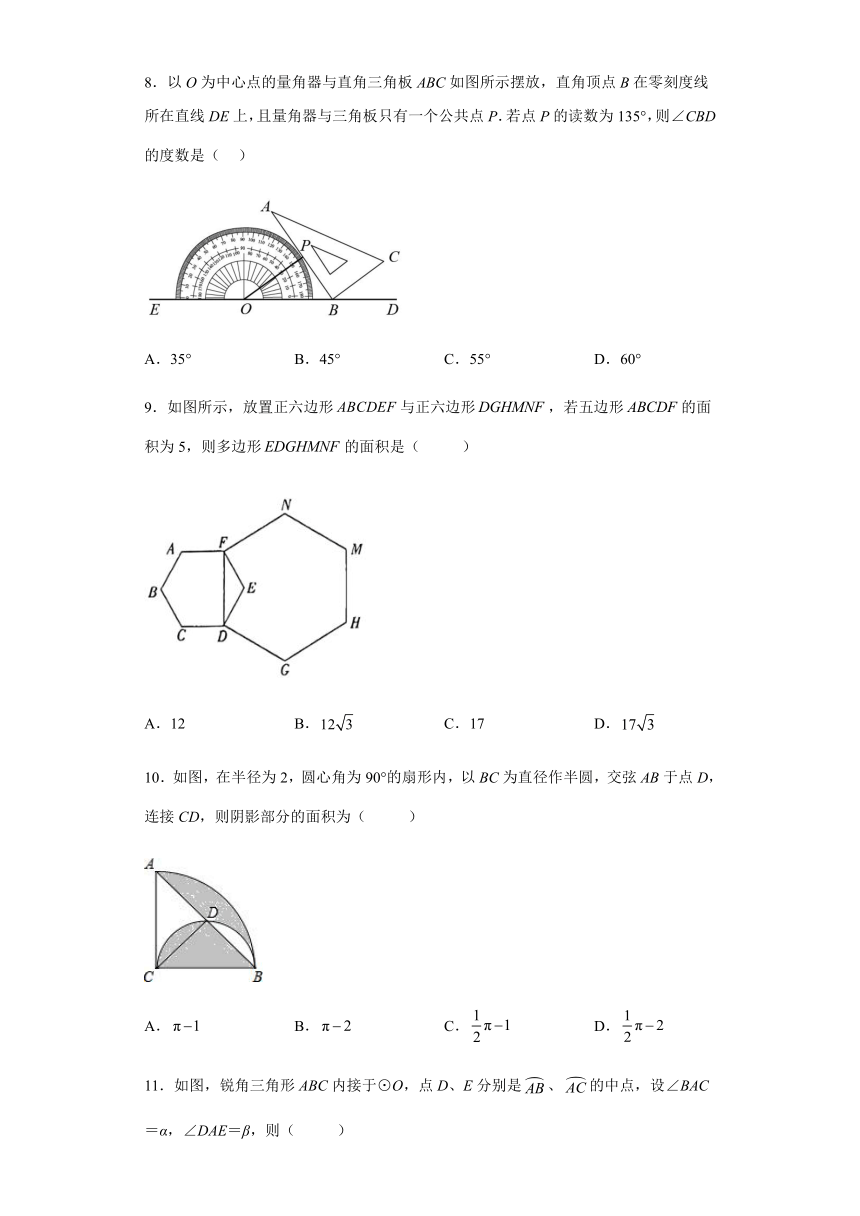
5.如图,点A,B,C是上的三个点,若,则的度数为( )
A.38° B.48° C.52° D.76°
6.小王不慎把一面圆形镜子打碎了,其中三块如图所示,三块碎片中最有可能配到与原来一样大小的圆形镜子的碎片是( )
A.① B.② C.③ D.都不能
7.如图,△ABC的内切圆⊙O分别与AB,BC,AC相切于点D,E,F,且AD=2,BC=5,则△ABC的周长为( )
A.16 B.14 C.12 D.10
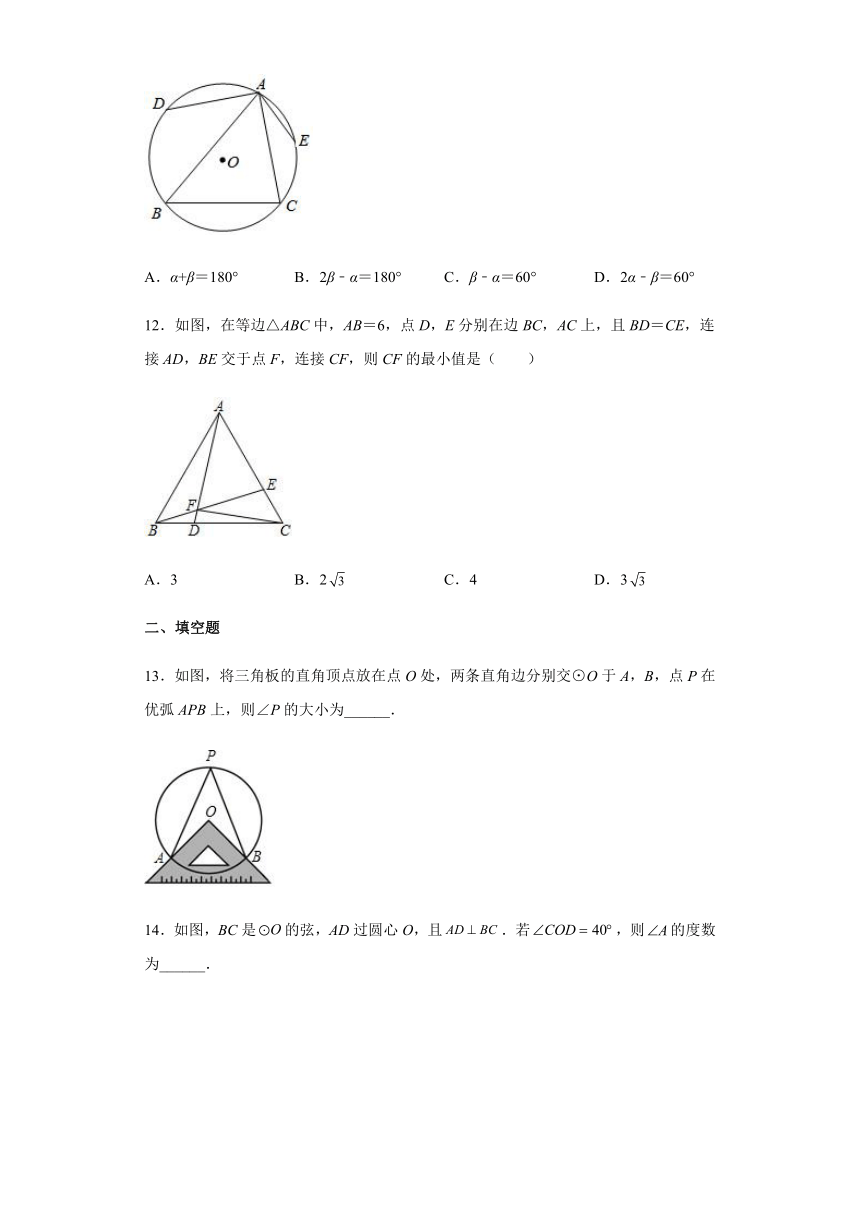
8.以O为中心点的量角器与直角三角板ABC如图所示摆放,直角顶点B在零刻度线所在直线DE上,且量角器与三角板只有一个公共点P.若点P的读数为135°,则∠CBD的度数是( )
A.35° B.45° C.55° D.60°
9.如图所示,放置正六边形与正六边形,若五边形的面积为5,则多边形的面积是( )
A.12 B. C.17 D.
10.如图,在半径为2,圆心角为90°的扇形内,以BC为直径作半圆,交弦AB于点D,连接CD,则阴影部分的面积为( )
A. B. C. D.
11.如图,锐角三角形ABC内接于⊙O,点D、E分别是、的中点,设∠BAC=α,∠DAE=β,则( )
A.α+β=180° B.2β﹣α=180° C.β﹣α=60° D.2α﹣β=60°
12.如图,在等边△ABC中,AB=6,点D,E分别在边BC,AC上,且BD=CE,连接AD,BE交于点F,连接CF,则CF的最小值是( )
A.3 B.2 C.4 D.3
二、填空题
13.如图,将三角板的直角顶点放在点O处,两条直角边分别交⊙O于A,B,点P在优弧APB上,则∠P的大小为______.
14.如图,BC是的弦,AD过圆心O,且.若,则的度数为______.
15.一圆锥的侧面展开图的圆心角为,底面半径为3,则该圆锥的侧面积为_______.
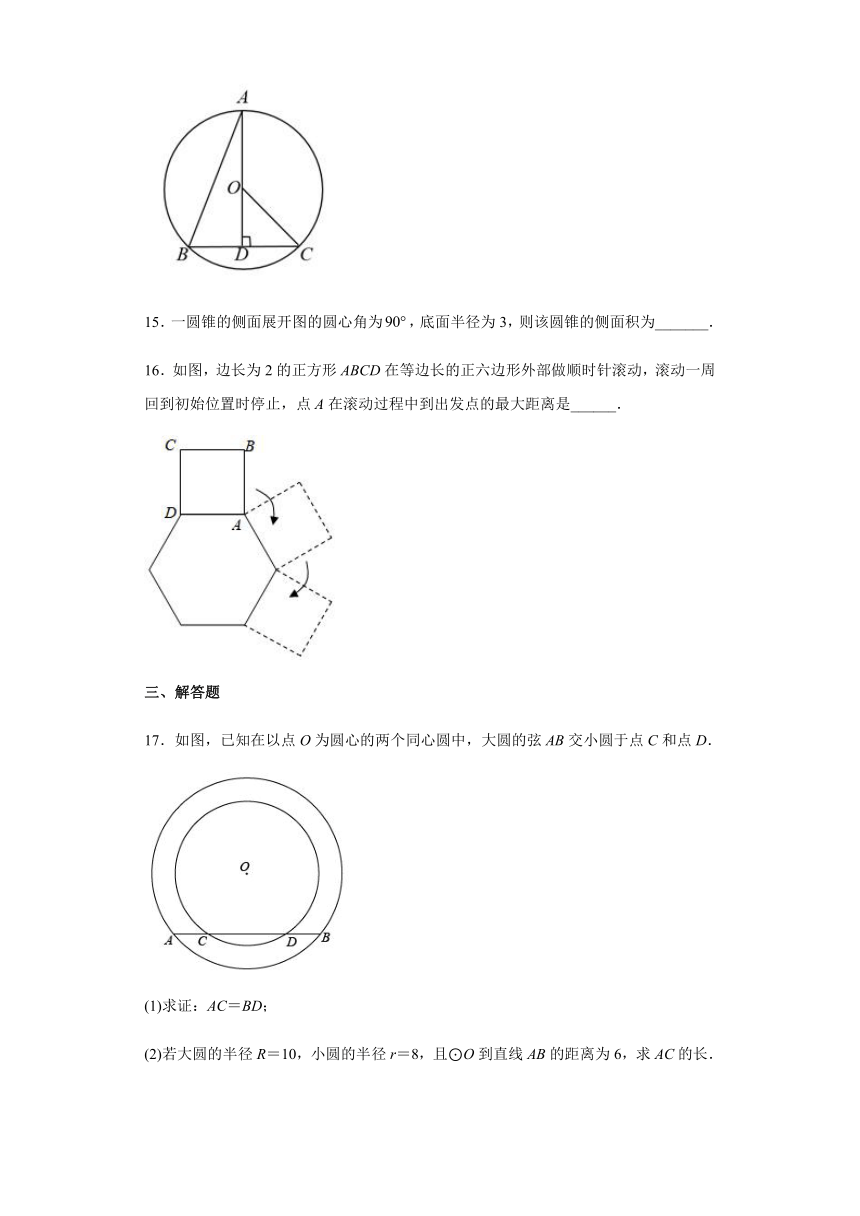
16.如图,边长为2的正方形ABCD在等边长的正六边形外部做顺时针滚动,滚动一周回到初始位置时停止,点A在滚动过程中到出发点的最大距离是______.
三、解答题
17.如图,已知在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C和点D.
(1)求证:AC=BD;
(2)若大圆的半径R=10,小圆的半径r=8,且⊙O到直线AB的距离为6,求AC的长.
18.如图,已知AB为⊙O的直径,CD是弦,且AB⊥CD于点E,连接AC、OC、BC.
(1)求证:∠ACO=∠BCD;
(2)若EB=8cm,CD=24cm,求⊙O的半径.
19.如图,已知AB是⊙O的直径,C是⊙O上的点,过点C作⊙O的切线,交AB的延长线上于点D,连接BC.
(1)求证:∠BCD=∠BAC;
(2)若∠D=30°,BD=2,求图中阴影部分的面积.
20.如图,已知AB是⊙O的直径,点C在⊙O上,AD⊥DC于点D,AC平分∠DAB.
(1)求证:直线CD是⊙O的切线;
(2)若AD=3,∠DAC=30°,求⊙O的面积.
21.如图,AB是⊙O的直径,点C是劣弧BD中点,AC与BD相交于点E.连接BC,∠BCF=∠BAC,CF与AB的延长线相交于点F.
(1)求证:CF是⊙O的切线;
(2)求证:∠ACD=∠F;
(3)若AB=10,BC=6,求AD的长.
试卷第1页,共3页
答案
1.C
2.D
3.B
4.D
5.A
6.B
7.B
8.B
9.C
10.A
11.B
12.B
13.45°
14.20°
15.
16.
17.(1)过点O作,垂足为E,如图
则CE=DE,AE=BE,
,
即.
(2)连接OA,OC,如图所示,
在中,,,
,
在中,,,
,
.
18.证明:(1)∵AB为⊙O的直径,
∴∠ACB=90°,
∴∠BCD与∠ACE互余,
又∵AB⊥CD于点E,
∴∠ACE与∠CAE互余,
∴∠BCD=∠BAC.
∵OA=OC,
∴∠OAC=∠OCA.
∴∠ACO=∠BCD;
(2)设⊙O的半径为Rcm,则OE=OB﹣EB=(R﹣8)cm,
CE=CD=×24=12cm,
在Rt△CEO中,由勾股定理可得:
OC2=OE2+CE2,
即R2=(R﹣8)2+122,
解得R=13.
答:⊙O的半径为13cm.
19.(1)证明:如图,连接OC,
∵CD为⊙O的切线,
∴OC⊥CD,
∴∠BCD+∠OCB=90°,
∵AB是直径,
∴∠ACB=90°,
∴∠OCA+OCB =90°,
∴∠OCA=∠BCD,
又∵OA=OC,
∴∠BAC=∠OCA,
∴∠BCD=∠BAC.
(2)解:设⊙O的半径为r,
∴AB=2r,
∵∠D=30°,∠OCD=90°,
∴OD=2OC=2r,∠COB=60°,
∵OD=OB+BD,
∴r+2=2r,
解得r=2,
∴BC为斜边上的中线,
∴BC=OD =2,
又∵中,AB=2r=4,
由勾股定理可知,
∵OA=OB,
∴ ,
∵∠AOC=180°-∠COB=120°,
∴S扇形OAC=,
∴阴影部分面积为.
20.(1)证明:连接,
,
,
平分,
,
,
,
,
为的切线
(2)解:连接BC,
∵是的直径,
,
平分,,
,
,
,
的面积=.
21.(1)解:如图,连接OC
∵AB是直径
∴∠ACB=90°
∴∠ACO+∠OCB=90°
∵OA=OC
∴∠BAC=∠ACO
∵∠BCF=∠BAC
∴∠BCF +∠OCB=90°
∴∠OCF=90°
∴OC⊥CF
∴CF是⊙O的切线
(2)∵点C是劣弧BD中点
∴∠CAD=∠BAC
∵∠BCF=∠BAC
∴∠CAD=∠BCF
∴∠CAD=∠CBD
∴∠BCF=∠CBD
∴CF∥BD
∴∠ABD=∠F
∴∠ACD=∠ABD
∴∠ACD=∠F
(3),
∴点H为BD的中点
∵AB=10,BC=6
设OH=x,则CH=5-x,根据勾股定理得
解得:
∵OH是中位线
∴
答案第1页,共2页
一、单选题
1.下列说法中,正确的是( )
A.相等的圆心角所对的弧相等
B.过任意三点可以画一个圆
C.周长相等的圆是等圆
D.平分弦的直径垂直于弦
2.如图,CD为的直径,弦于点E,,,则直径CD的长是( )
A.4 B.8 C.26 D.10
3.如图在平面直角坐标系中,过格点A,B,C作一圆弧,圆心坐标是( )
A. B. C. D.
4.如图,⊙O为△ABC的外接圆,且AB为⊙O的直径,若OC=AC=5,则BC长为( )
A.10 B.9 C.8 D.5
5.如图,点A,B,C是上的三个点,若,则的度数为( )
A.38° B.48° C.52° D.76°
6.小王不慎把一面圆形镜子打碎了,其中三块如图所示,三块碎片中最有可能配到与原来一样大小的圆形镜子的碎片是( )
A.① B.② C.③ D.都不能
7.如图,△ABC的内切圆⊙O分别与AB,BC,AC相切于点D,E,F,且AD=2,BC=5,则△ABC的周长为( )
A.16 B.14 C.12 D.10
8.以O为中心点的量角器与直角三角板ABC如图所示摆放,直角顶点B在零刻度线所在直线DE上,且量角器与三角板只有一个公共点P.若点P的读数为135°,则∠CBD的度数是( )
A.35° B.45° C.55° D.60°
9.如图所示,放置正六边形与正六边形,若五边形的面积为5,则多边形的面积是( )
A.12 B. C.17 D.
10.如图,在半径为2,圆心角为90°的扇形内,以BC为直径作半圆,交弦AB于点D,连接CD,则阴影部分的面积为( )
A. B. C. D.
11.如图,锐角三角形ABC内接于⊙O,点D、E分别是、的中点,设∠BAC=α,∠DAE=β,则( )
A.α+β=180° B.2β﹣α=180° C.β﹣α=60° D.2α﹣β=60°
12.如图,在等边△ABC中,AB=6,点D,E分别在边BC,AC上,且BD=CE,连接AD,BE交于点F,连接CF,则CF的最小值是( )
A.3 B.2 C.4 D.3
二、填空题
13.如图,将三角板的直角顶点放在点O处,两条直角边分别交⊙O于A,B,点P在优弧APB上,则∠P的大小为______.
14.如图,BC是的弦,AD过圆心O,且.若,则的度数为______.
15.一圆锥的侧面展开图的圆心角为,底面半径为3,则该圆锥的侧面积为_______.
16.如图,边长为2的正方形ABCD在等边长的正六边形外部做顺时针滚动,滚动一周回到初始位置时停止,点A在滚动过程中到出发点的最大距离是______.
三、解答题
17.如图,已知在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C和点D.
(1)求证:AC=BD;
(2)若大圆的半径R=10,小圆的半径r=8,且⊙O到直线AB的距离为6,求AC的长.
18.如图,已知AB为⊙O的直径,CD是弦,且AB⊥CD于点E,连接AC、OC、BC.
(1)求证:∠ACO=∠BCD;
(2)若EB=8cm,CD=24cm,求⊙O的半径.
19.如图,已知AB是⊙O的直径,C是⊙O上的点,过点C作⊙O的切线,交AB的延长线上于点D,连接BC.
(1)求证:∠BCD=∠BAC;
(2)若∠D=30°,BD=2,求图中阴影部分的面积.
20.如图,已知AB是⊙O的直径,点C在⊙O上,AD⊥DC于点D,AC平分∠DAB.
(1)求证:直线CD是⊙O的切线;
(2)若AD=3,∠DAC=30°,求⊙O的面积.
21.如图,AB是⊙O的直径,点C是劣弧BD中点,AC与BD相交于点E.连接BC,∠BCF=∠BAC,CF与AB的延长线相交于点F.
(1)求证:CF是⊙O的切线;
(2)求证:∠ACD=∠F;
(3)若AB=10,BC=6,求AD的长.
试卷第1页,共3页
答案
1.C
2.D
3.B
4.D
5.A
6.B
7.B
8.B
9.C
10.A
11.B
12.B
13.45°
14.20°
15.
16.
17.(1)过点O作,垂足为E,如图
则CE=DE,AE=BE,
,
即.
(2)连接OA,OC,如图所示,
在中,,,
,
在中,,,
,
.
18.证明:(1)∵AB为⊙O的直径,
∴∠ACB=90°,
∴∠BCD与∠ACE互余,
又∵AB⊥CD于点E,
∴∠ACE与∠CAE互余,
∴∠BCD=∠BAC.
∵OA=OC,
∴∠OAC=∠OCA.
∴∠ACO=∠BCD;
(2)设⊙O的半径为Rcm,则OE=OB﹣EB=(R﹣8)cm,
CE=CD=×24=12cm,
在Rt△CEO中,由勾股定理可得:
OC2=OE2+CE2,
即R2=(R﹣8)2+122,
解得R=13.
答:⊙O的半径为13cm.
19.(1)证明:如图,连接OC,
∵CD为⊙O的切线,
∴OC⊥CD,
∴∠BCD+∠OCB=90°,
∵AB是直径,
∴∠ACB=90°,
∴∠OCA+OCB =90°,
∴∠OCA=∠BCD,
又∵OA=OC,
∴∠BAC=∠OCA,
∴∠BCD=∠BAC.
(2)解:设⊙O的半径为r,
∴AB=2r,
∵∠D=30°,∠OCD=90°,
∴OD=2OC=2r,∠COB=60°,
∵OD=OB+BD,
∴r+2=2r,
解得r=2,
∴BC为斜边上的中线,
∴BC=OD =2,
又∵中,AB=2r=4,
由勾股定理可知,
∵OA=OB,
∴ ,
∵∠AOC=180°-∠COB=120°,
∴S扇形OAC=,
∴阴影部分面积为.
20.(1)证明:连接,
,
,
平分,
,
,
,
,
为的切线
(2)解:连接BC,
∵是的直径,
,
平分,,
,
,
,
的面积=.
21.(1)解:如图,连接OC
∵AB是直径
∴∠ACB=90°
∴∠ACO+∠OCB=90°
∵OA=OC
∴∠BAC=∠ACO
∵∠BCF=∠BAC
∴∠BCF +∠OCB=90°
∴∠OCF=90°
∴OC⊥CF
∴CF是⊙O的切线
(2)∵点C是劣弧BD中点
∴∠CAD=∠BAC
∵∠BCF=∠BAC
∴∠CAD=∠BCF
∴∠CAD=∠CBD
∴∠BCF=∠CBD
∴CF∥BD
∴∠ABD=∠F
∴∠ACD=∠ABD
∴∠ACD=∠F
(3),
∴点H为BD的中点
∵AB=10,BC=6
设OH=x,则CH=5-x,根据勾股定理得
解得:
∵OH是中位线
∴
答案第1页,共2页
