2021-2022学年人教版数学八年级下册18.2.3正方形(性质)课时练习(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版数学八年级下册18.2.3正方形(性质)课时练习(Word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 574.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-21 00:00:00 | ||
图片预览


文档简介
正方形(性质)
一、单选题
1.下列性质中,平行四边形,矩形,菱形,正方形共有的性质是( )
A.对角线相等 B.对角线互相垂直
C.对角线互相平分 D.对角线平分内角
2.正方形的一条对角线长为2,则正方形的周长为( )
A.4 B.8 C. D.
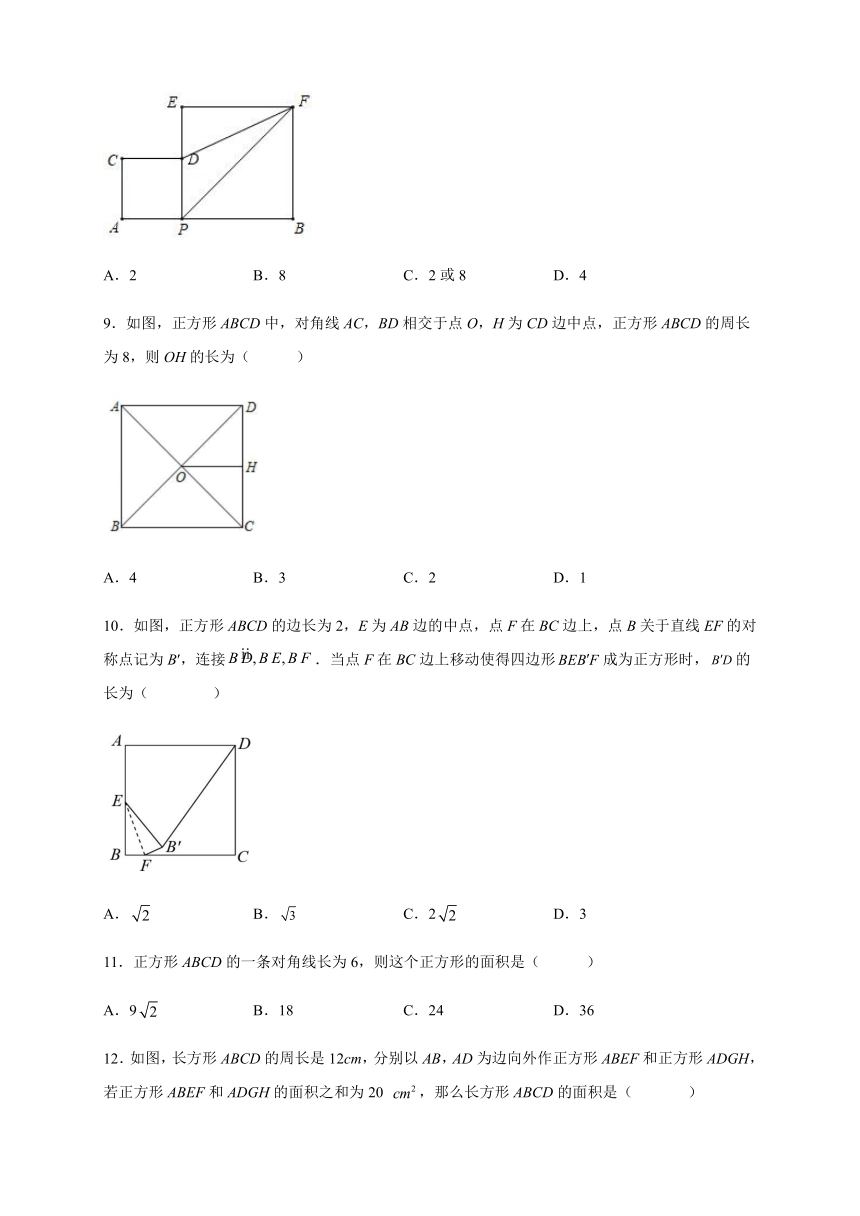
3.如图,直线l上有三个正方形A、B、C,若正方形A、C的边长分别为5和7,则正方形B的面积为()
A.36 B.49 C.74 D.81
4.如图,延长正方形的边至点E,使得.连结交边于点F,则的大小是( )
A.105度 B.112.5度 C.120度 D.135度
5.如图,在正方形ABCD中,E、F是对角线BD上的点,AB=BF=DE,则∠EAF的度数为( )
A.22.5° B.30° C.45° D.67.5°
6.如图,正方形ABCD中,点F为AB上一点,CF与BD交于点E,连接AE,若∠BCF=20°,则∠AEF的度数( )
A.35° B.40° C.45° D.50°
7.如图,在平面直角坐标系中,四边形ABCD为正方形,点A的坐标为,点B的坐标为,点E为对角线的交点,点F与点E关于y轴对称,则点F的坐标为( )
A. B. C. D.
8.如图,点P是线段AB上任意一点,在AB同侧作正方形ACDP、正方形PEFB,连接DF、PF,已知AB=10,当△PDF的面积为8时,AP的长为( )
A.2 B.8 C.2或8 D.4
9.如图,正方形ABCD中,对角线AC,BD相交于点O,H为CD边中点,正方形ABCD的周长为8,则OH的长为( )
A.4 B.3 C.2 D.1
10.如图,正方形ABCD的边长为2,E为AB边的中点,点F在BC边上,点B关于直线EF的对称点记为B′,连接.当点F在BC边上移动使得四边形成为正方形时,的长为( )
A. B. C.2 D.3
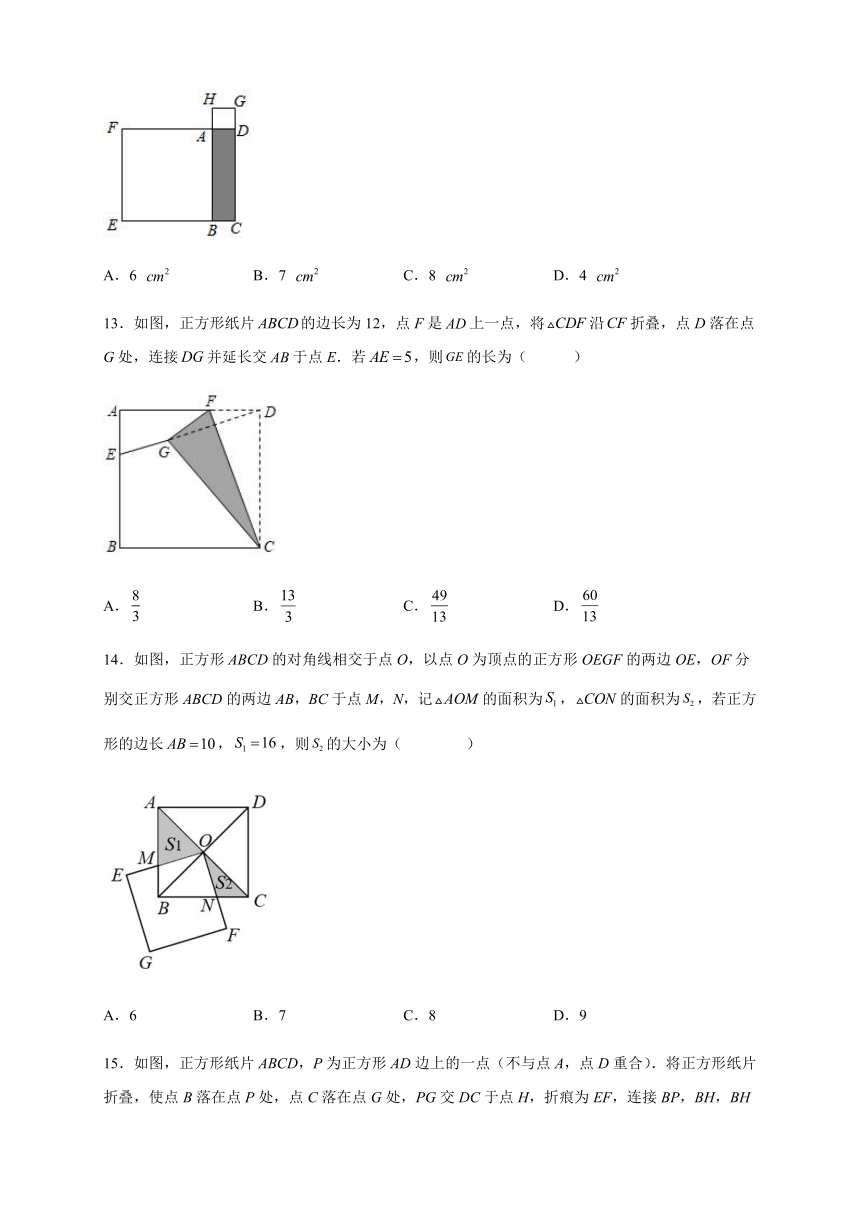
11.正方形ABCD的一条对角线长为6,则这个正方形的面积是( )
A.9 B.18 C.24 D.36
12.如图,长方形ABCD的周长是12cm,分别以AB,AD为边向外作正方形ABEF和正方形ADGH,若正方形ABEF和ADGH的面积之和为20 ,那么长方形ABCD的面积是( )
A.6 B.7 C.8 D.4
13.如图,正方形纸片的边长为12,点F是上一点,将沿折叠,点D落在点G处,连接并延长交于点E.若,则的长为( )
A. B. C. D.
14.如图,正方形ABCD的对角线相交于点O,以点O为顶点的正方形OEGF的两边OE,OF分别交正方形ABCD的两边AB,BC于点M,N,记的面积为,的面积为,若正方形的边长,,则的大小为( )
A.6 B.7 C.8 D.9
15.如图,正方形纸片ABCD,P为正方形AD边上的一点(不与点A,点D重合).将正方形纸片折叠,使点B落在点P处,点C落在点G处,PG交DC于点H,折痕为EF,连接BP,BH,BH交EF于点M,连接PM.下列结论:①BE=PE;②BP=EF;③PB平分∠APG;④PH=AP+HC;⑤MH=MF,其中正确结论的个数是( )
A.5 B.4 C.3 D.2
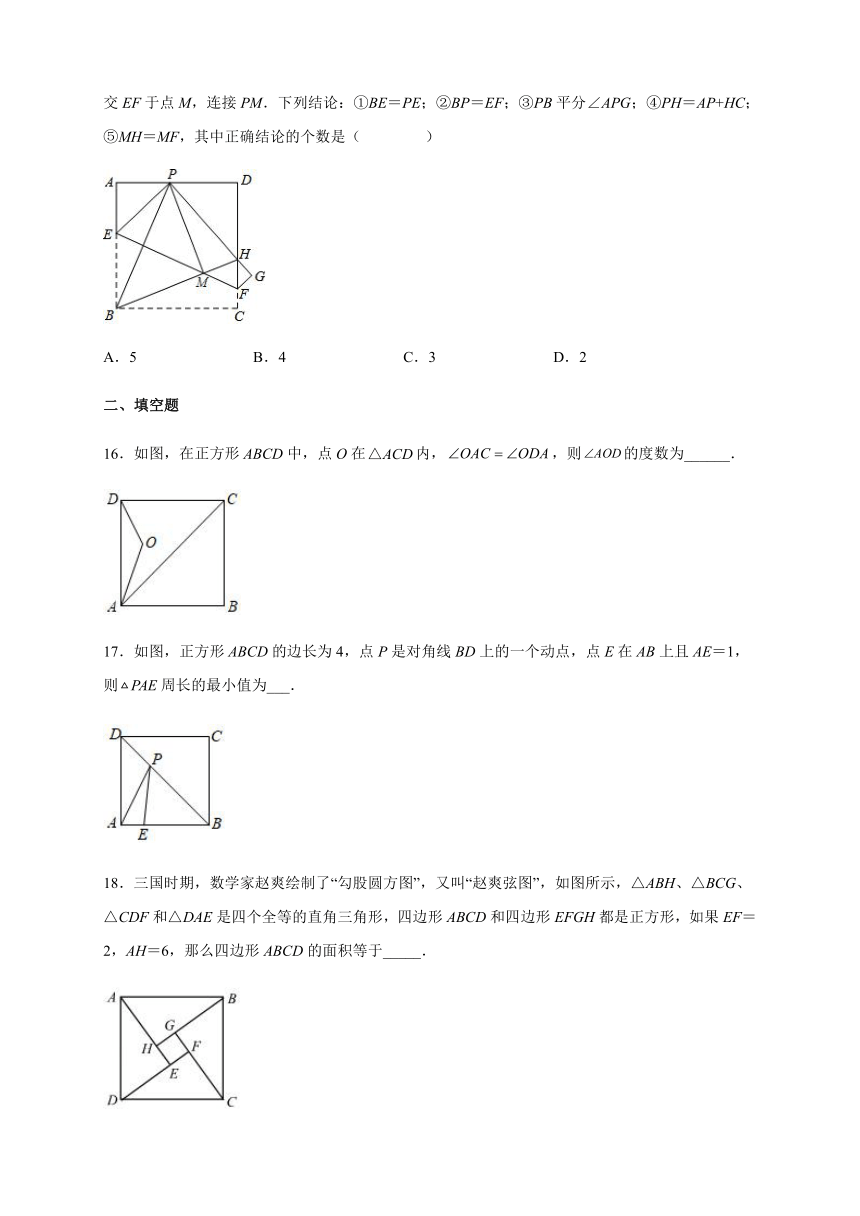
二、填空题
16.如图,在正方形ABCD中,点O在内,,则的度数为______.
17.如图,正方形ABCD的边长为4,点P是对角线BD上的一个动点,点E在AB上且AE=1,则PAE周长的最小值为___.
18.三国时期,数学家赵爽绘制了“勾股圆方图”,又叫“赵爽弦图”,如图所示,△ABH、△BCG、△CDF和△DAE是四个全等的直角三角形,四边形ABCD和四边形EFGH都是正方形,如果EF=2,AH=6,那么四边形ABCD的面积等于_____.
19.如图所示,正方形的边长为1,其面积标记为,以为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为,…,按照此规律继续下去,则的值为_________.
20.如图,RtABC中,∠ACB=90°,AC=4,BC=3,以AB,BC,AC为边在AB同侧作正方形ABDE,正方形BCFG,正方形ACMN,点E恰好在边MN上,GF的延长线能经过点D.图中阴影部分的面积为_____________.
三、解答题
21.如图,点E是正方形ABCD外一点,点F是线段AE上一点,且△EBF是等腰直角三角形,其中∠EBF=90°,连接CE、CF.求证:AF=CE.
22.如图:正方形ABCD中,点E、F分别在边BC、CD上,BE=CF,连接AE,BF交于点O,点M为AB中点,连接OM,求证:.
23.如图,在正方形ABCD中,E是BC的中点,连接AE,过点B作射线BM交CD于点F,
交AE于点O,且BF⊥AE .
(1)求证:BF=AE;
(2)连接OD,猜想OD与AB的数量关系,并证明.
24.在正方形ABCD中,点F是边AB上一点,连接DF,点E为DF中点.连接BE、CE、AE.
(1)求证:△AEB≌△DEC;
(2)当EB=BC时,求∠AFD的度数.
25.在边长为1的正方形ABCD中,点E是射线BC上一动点,AE与BD相交于点M,AE或其延长线与DC或其延长线相交于点F,G是EF的中点,连接CG.
(1)如图1,当点E在BC边上时.求证:CG⊥CM.
(2)如图2,当点E在BC的延长线上时,(1)中的结论是否成立?请说明理由.
(3)在点E运动过程中,当BE的长度多少时,△MCE是等腰三角形?请说明理由.
试卷第1页,共3页
参考答案:
1.C
解:∵平行四边形的对角线互相平分,
∴矩形,菱形,正方形的对角线也必然互相平分.
故选:C.
2.D
解:因为正方形的一条对角线长为2,
设正方形的边长为,
根据勾股定理,得,
解得,
所以正方形的边长为,
则正方形的周长为.
故选:D.
3.C
解:根据正方形的性质得出∠EFG=∠EGH=∠HMG=90°,EG=GH,
∵∠FEG+∠EGF=90°,∠EGF+∠HGM=90°,
∴∠FEG=∠HGM,
在△EFG和△GMH中,
,
∴△EFG≌△GMH(AAS),
∴FG=MH,GM=EF,
∵A,C的边长分别为5和7,
∴EF2=52, HM2=72,
∴B的面积为EG2=EF2+FG2=EF2+HM2=25+49=74,
故答案为:C.
4.B
解:∵AC是正方形的对角线,
∴AC平分∠BCD,且∠BCD=90°,
∴∠ACD=∠ACB=45°,
∵∠DCE=∠BCD=90°,
∴∠ACE=∠ACD+∠DCE=45°+90°=135°,
∵AC=CE,
∴∠E=∠CAE=,
∴∠AFC=∠FDE+∠E=90°+22.5°=112.5°.
故选择B.
5.C
解:在正方形中,,,,
,
,
,
.
故选:C.
6.D
解:∵四边形ABCD是正方形,
∴∠ABC=90°,BC=BA,∠ABE=∠CBE=45°.
又BE=BE,
∴△ABE≌△CBE(SAS).
∴∠BAE=∠BCE=20°.
∵∠ABC=90°,∠BCF=20°
∴∠BFC=180°-∠ABC-∠BCF
=180°-90°-20°
=70°
∵∠BFC=∠BAE+∠AEF
∴∠AEF=∠BFC-∠BAE=70°-20°=50°
故选:D.
7.D
解:∵点A的坐标为(0,2),点B的坐标为(4,0),
∴OA=2,OB=4,
过D作DH⊥y轴于H,如图,
∵四边形ABCD是正方形,
∴AD=AB,∠DAB=90°,DE=BE,
∵∠AHD=∠AOB=90°,
∴∠DAH+∠AHD=∠AHD+∠BAO=90°,
∴∠ADH=∠BAO,
∴△ADH≌△BAO(AAS),
∴AH=OB=4,DH=OA=2,
∴OH=6,
∴D(2,6),
∵点E是BD的中点,点B的坐标为(4,0),
∴点E的坐标是(,),
∴E(3,3),
∵点F与点E关于y轴对称,
点F的坐标为(﹣3,3),
故选:D.
8.C
解:设,则,
四边形和四边形都是正方形,
,
,
即,解得或,
故选:C.
9.D
解:由题意知是的中位线
∴
∵正方形ABCD的周长为8
∴
∴
故选D.
10.A
解:如图,连接BB',连接BD,
∵四边形ABCD是正方形,且边长为2,
∴BD=AB=,BD平分∠ABC,
∵点E是AB的中点,
∴AE=BE=1,
∵四边形是正方形,
∴,平分∠ABC,
∴点B,点,点D三点共线,
∴.
故选:A.
11.B
解:在正方形中,对角线相等,所以正方形ABCD的对角线长均为6,
∵正方形又是菱形,菱形的面积计算公式是(a、b是正方形对角线长度)
∴,
故选:B.
12.C
解:设AB=x,AD=y,
∵长方形ABCD的周长是12cm,正方形ABEF和ADGH的面积之和为20 ,
∴x+y=6,,
∴,
∴,
∴,
故选C.
13.C
解:设CF与DE交于点O,
将△CDF沿CF折叠,点D落在点G处,
GO=DO, CF⊥DG,
四边形ABCD是正方形,
AD=CD,∠A=∠ADC=90°=∠FOD, ,
∠CFD+∠FCD=90°=∠CFD+∠ADE,
∠ADE=∠FCD,
在△ADE和△DCF中,
( ASA ),
AE=DF=5,
AE=5, AD=12,
DE=,
CF⊥DG, ,
,
,
DO==GO,
EG=
故答案为:C
14.D
解:∵正方形ABCD的对角线AC,BD交于点O,
∴OC=OD=BO=AO,∠ABO=∠ACB=45°,AC⊥BD.
∵∠MOB+∠BON=90°,∠BON+∠CON=90°
∴∠BOM=∠CON,且OC=OB,∠ABO=∠ACB=45°,
∴△BOM≌△CON(ASA),=S△BOM,
∴,
∵=S正方形ABCD,正方形的边长,,
∴=S正方形ABCD -=.
故选:D.
15.B
解:∵折痕为EF,
∴四边形EBCF与四边形EPGF全等
∴BE=PE,
故①正确;
如图2,作FK⊥AB于K.设EF交BP于O.
∵四边形ABCD为正方形,
∴AB=BC,∠A=∠ABC=∠C=90°,
∵FK⊥AB,
∴∠FKB=90°,
∴∠FKB=∠KBC=∠C=90°,
∴四边形BCFK是矩形,
∴KF=BC=AB,
∵EF为对称轴,点B与点P为对称点,
∴EF⊥PB,
∴∠BOE=90°,
∵∠ABP+∠BEO=90°,∠BEO+∠EFK=90°,
∴∠ABP=∠EFK,
在△ABP和△KFE中,
,
∴△ABP≌△KFE(ASA),
∴EF=BP,故②正确,
∵BE=PE,
∴∠EBP=∠EPB.
又∵∠EPH=∠EBC=90°,
∴∠EPH﹣∠EPB=∠EBC﹣∠EBP.
即∠PBC=∠BPH.
又∵AD∥BC,
∴∠APB=∠PBC.
∴∠APB=∠BPH.故③正确;
如图3,过B作BQ⊥PH,垂足为Q.
∴∠PQB=∠HQB=90°,
由(1)知∠APB=∠BPH,
在△APB和△QPB中,
,
∴△ABP≌△QBP(AAS),
∴AP=QP,AB=QB,
又∵AB=BC,
∴BC=BQ.
∵∠HQB=90°,∠C=90°
在Rt△BCH和Rt△BQH中
,
∴Rt△BCH≌Rt△BQH(HL),
∴CH=QH,
∴QP+QH=AP+CH,即PH=AP+CH,故④正确;
设EF与BP的交点为点N,如图4,
∵Rt△ABP≌Rt△QBP,△BCH≌△BQH,
∴∠ABP=∠QBP,∠CBH=∠QBH,
∴∠QBP+∠QBH=∠ABP+∠CBH,
即∠PBM=45°,
由折叠知,∠BPM=∠PBM=45°,∠EBM=∠EPM,∠PNF=∠BNF=90°,
∵AB∥CD,
∴∠MHF=∠EBM=∠EPM=45°+∠EPN,
∵在四边形DPNF中,∠D=∠PNF=90°,
∴∠MFH+∠DPN=180°,
∵∠DPN+∠APN=180°,
∴∠APN=∠MFH,
假设MH=MF,
∴∠MHF=∠MFH=∠APB,
在△ABP和△CBH中,
,
∴△ABP≌△CBH(AAS),
∴∠ABP=∠CBH,
∵∠ABP+∠CBH=45°,
∴∠ABP=∠CBH=22.5°,
∵点P在AD上,
∴0≤∠ABP≤45°,
∴∠ABP=22.5°与0≤∠ABP≤45°相矛盾,
∴假设不正确,故⑤错误.
故选:B.
16.135°
解:∵四边形ABCD是正方形,
∴∠CAD=45°,
∴∠OAC+∠OAD=45°,
又∵∠OAC=∠ODA,
∴∠ODA+∠OAD=45°,
∴∠AOD=180°-∠ODA-∠OAD=135°,
故答案为:135°.
17.6
解:连接CP,CE,
∵四边形ABCD是正方形,
∴AB=BC,∠ABD=∠CBP,
在△ABP和△CBP中,
,
∴△ABP≌△CBP(SAS),
∴AP=CP,
∴AP+PE最小值为CE的长,
∵AE=1,
∴BE=AB AE=3,
在Rt△CBE中,由勾股定理得:
CE=,
∴△PAE周长的最小值为CE+AE=5+1=6,
故答案为:6.
18.
解:∵四边形EFGH是正方形
∴GH=EF=2
∵△ABH≌△BCG
∴BG=AH=6
∴BH=BG+GH=6+2=8
∴
∵ △ABH、△BCG、△CDF和△DAE是四个全等的直角三角形
∴这四个直角三角形的面积均为24
∵四边形EFGH是正方形
∴
∴
故答案为:100
19.
解:由题意知,面积为的正方形的边长为1,
面积为的正方形的边长为,
面积为的正方形的边长为,
面积为的正方形的边长为,
……
推导一般性规律为:
∴
故答案为:.
20.13
解:解:如图,设CF与BD交于点Q,
∵∠ACB=90°,AC=4,BC=3
∴在Rt中,利用勾股定理得:
∵四边形ABDE是正方形,
∴∠ABQ=∠D=∠ACB=90°,AB=BD,
∴∠ABC+∠CAB=90°,∠ABC+∠PBD=90°,
∴∠PBD =∠CAB,
∴≌,
∴=,
∴-=-
即:=,
∴S阴=S正方形ABDE-2S△ABC==25-12=13,
故答案为13.
21.见解析
证明:∵正方形ABCD
∴BC=AB,∠ABC=90°,
∴∠EBF=∠ABC=90°,
∴∠ABF+∠FBC=∠CBE+∠FBC
∴∠ABF=∠CBE,
又∵BF=BE,
∴△ABF≌△CBE(SAS),
∴AF=CE.
22.见解析
证明:∵四边形ABCD是正方形,
∴AB=BC,∠ABE=∠BCF=90°,
又BE=CF,
∴△ABE≌△BCF(SAS).
∴∠BAE=∠CBF.
∵∠ABO+∠CBF=90°,
∴∠ABO+∠BAO=90°,即∠AOB=90°.
在Rt△ABO中,M点是斜边AB中点,
∴.
23.(1)见解析 (2)OD=AB,理由见解析
(1)
证明:在正方形ABCD中,∠ABC=∠C=90°,AB=BC,
∴∠BAE+∠AEB=90°,
∵BF⊥AE,
∴∠EOB=90°,
∴∠CBF+∠AEB=90°,
∴∠BAE=∠CBF,
∴△ABE≌△BCF,
∴BF=AE;
(2)
解:OD=AB,理由如下:
如图,延长AD交射线BM于点G,
由(1)得:△ABE≌△BCF,
∴BE=CF,
∵E是BC的中点,
∴,
∴CF=DF,
∵AD∥BC,
∴∠DGF=∠CBF,
在△DGF和△CBF中,
∵∠DGF=∠CBF,∠DFG=∠BFC,DF=CF,
∴△DGF≌△CBF,
∴DG=BC,
∴DG=AD,即OD为△AOG的中线,
∵BF⊥AE,
∴.
24.(1)见详解; (2)∠AFE=75°.
(1)
证明:∵四边形ABCD为正方形,
∴AB=DC,∠FAD=90°=∠CDA,
∵点E为DF中点.
∴AE=FE=DE,
∴∠EAD=∠EDA,
∴∠BAE-∠EAD=∠CDA-∠EDA,即∠BAE=∠CDE,
在△AEB和△DEC,
,
∴△AEB≌△DEC(SAS);
(2)
解:∵△AEB≌△DEC;
∴BE=CE,
∵EB=BC,
∴BC=BE=CE,
∴∠EBC=∠ECB=∠BEC=60°
∴∠EBF=90°-∠EBC=90°-60°=30°,∠ECD=90°-∠ECB=90°-60°=30°,
∵CE=BC=CD,
∴∠DEC=∠EDC=,
∴∠FEB=180°-∠BEC-∠CED=180°-60°-75°=45°,
∵∠AFE为△FBE的外角,
∴∠AFE=∠FBE+∠FEB=30°+45°=75°.
25.(1)证明见解析 (2)成立,理由见解析 (3)戓,理由见解析
(1)
解:∵四边形ABCD是正方形,
∴AB=BC,∠ABM=∠CBM,
在△ABM和△CBM中,
,
∴△ABM≌△CBM(SAS).
∴∠BAM=∠BCM,
又∵∠ECF=90°,G是EF的中点,
∴GC=EF=GF,
∴∠GCF=∠GFC,
又∵AB∥DF,
∴∠BAM=∠GFC,
∴∠BCM=∠GCF,
∴∠BCM+∠GCE=∠GCF+∠GCE=90°,
∴GC⊥CM;
(2)
解:成立;理由如下:
∵四边形ABCD是正方形,
∴AB=BC,∠ABM=∠CBM,
在△ABM和△CBM中,
,
∴△ABM≌△CBM(SAS),
∴∠BAM=∠BCM,
又∵∠ECF=90°,G是EF的中点,
∴GC=GF,
∴∠GCF=∠GFC,
又∵AB∥DF,
∴∠BAM=∠GFC,
∴∠BCM=∠GCF,
∴∠GCF+∠MCF=∠BCM+∠MCF=90°,
∴GC⊥CM;
(3)
解:分两种情况:①当点E在BC边上时,
∵∠MEC>90°,要使△MCE是等腰三角形,必须EM=EC,
∴∠EMC=∠ECM,
∴∠AEB=2∠BCM=2∠BAE,
∴2∠BAE+∠BAE=90°,
∴∠BAE=30°,
∴,
∵,
∴
∴;
②当点E在BC的延长线上时,同①知BE= .
综上①②,当BE=戓BE=时,△MCE是等腰三角形.
答案第1页,共2页
一、单选题
1.下列性质中,平行四边形,矩形,菱形,正方形共有的性质是( )
A.对角线相等 B.对角线互相垂直
C.对角线互相平分 D.对角线平分内角
2.正方形的一条对角线长为2,则正方形的周长为( )
A.4 B.8 C. D.
3.如图,直线l上有三个正方形A、B、C,若正方形A、C的边长分别为5和7,则正方形B的面积为()
A.36 B.49 C.74 D.81
4.如图,延长正方形的边至点E,使得.连结交边于点F,则的大小是( )
A.105度 B.112.5度 C.120度 D.135度
5.如图,在正方形ABCD中,E、F是对角线BD上的点,AB=BF=DE,则∠EAF的度数为( )
A.22.5° B.30° C.45° D.67.5°
6.如图,正方形ABCD中,点F为AB上一点,CF与BD交于点E,连接AE,若∠BCF=20°,则∠AEF的度数( )
A.35° B.40° C.45° D.50°
7.如图,在平面直角坐标系中,四边形ABCD为正方形,点A的坐标为,点B的坐标为,点E为对角线的交点,点F与点E关于y轴对称,则点F的坐标为( )
A. B. C. D.
8.如图,点P是线段AB上任意一点,在AB同侧作正方形ACDP、正方形PEFB,连接DF、PF,已知AB=10,当△PDF的面积为8时,AP的长为( )
A.2 B.8 C.2或8 D.4
9.如图,正方形ABCD中,对角线AC,BD相交于点O,H为CD边中点,正方形ABCD的周长为8,则OH的长为( )
A.4 B.3 C.2 D.1
10.如图,正方形ABCD的边长为2,E为AB边的中点,点F在BC边上,点B关于直线EF的对称点记为B′,连接.当点F在BC边上移动使得四边形成为正方形时,的长为( )
A. B. C.2 D.3
11.正方形ABCD的一条对角线长为6,则这个正方形的面积是( )
A.9 B.18 C.24 D.36
12.如图,长方形ABCD的周长是12cm,分别以AB,AD为边向外作正方形ABEF和正方形ADGH,若正方形ABEF和ADGH的面积之和为20 ,那么长方形ABCD的面积是( )
A.6 B.7 C.8 D.4
13.如图,正方形纸片的边长为12,点F是上一点,将沿折叠,点D落在点G处,连接并延长交于点E.若,则的长为( )
A. B. C. D.
14.如图,正方形ABCD的对角线相交于点O,以点O为顶点的正方形OEGF的两边OE,OF分别交正方形ABCD的两边AB,BC于点M,N,记的面积为,的面积为,若正方形的边长,,则的大小为( )
A.6 B.7 C.8 D.9
15.如图,正方形纸片ABCD,P为正方形AD边上的一点(不与点A,点D重合).将正方形纸片折叠,使点B落在点P处,点C落在点G处,PG交DC于点H,折痕为EF,连接BP,BH,BH交EF于点M,连接PM.下列结论:①BE=PE;②BP=EF;③PB平分∠APG;④PH=AP+HC;⑤MH=MF,其中正确结论的个数是( )
A.5 B.4 C.3 D.2
二、填空题
16.如图,在正方形ABCD中,点O在内,,则的度数为______.
17.如图,正方形ABCD的边长为4,点P是对角线BD上的一个动点,点E在AB上且AE=1,则PAE周长的最小值为___.
18.三国时期,数学家赵爽绘制了“勾股圆方图”,又叫“赵爽弦图”,如图所示,△ABH、△BCG、△CDF和△DAE是四个全等的直角三角形,四边形ABCD和四边形EFGH都是正方形,如果EF=2,AH=6,那么四边形ABCD的面积等于_____.
19.如图所示,正方形的边长为1,其面积标记为,以为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为,…,按照此规律继续下去,则的值为_________.
20.如图,RtABC中,∠ACB=90°,AC=4,BC=3,以AB,BC,AC为边在AB同侧作正方形ABDE,正方形BCFG,正方形ACMN,点E恰好在边MN上,GF的延长线能经过点D.图中阴影部分的面积为_____________.
三、解答题
21.如图,点E是正方形ABCD外一点,点F是线段AE上一点,且△EBF是等腰直角三角形,其中∠EBF=90°,连接CE、CF.求证:AF=CE.
22.如图:正方形ABCD中,点E、F分别在边BC、CD上,BE=CF,连接AE,BF交于点O,点M为AB中点,连接OM,求证:.
23.如图,在正方形ABCD中,E是BC的中点,连接AE,过点B作射线BM交CD于点F,
交AE于点O,且BF⊥AE .
(1)求证:BF=AE;
(2)连接OD,猜想OD与AB的数量关系,并证明.
24.在正方形ABCD中,点F是边AB上一点,连接DF,点E为DF中点.连接BE、CE、AE.
(1)求证:△AEB≌△DEC;
(2)当EB=BC时,求∠AFD的度数.
25.在边长为1的正方形ABCD中,点E是射线BC上一动点,AE与BD相交于点M,AE或其延长线与DC或其延长线相交于点F,G是EF的中点,连接CG.
(1)如图1,当点E在BC边上时.求证:CG⊥CM.
(2)如图2,当点E在BC的延长线上时,(1)中的结论是否成立?请说明理由.
(3)在点E运动过程中,当BE的长度多少时,△MCE是等腰三角形?请说明理由.
试卷第1页,共3页
参考答案:
1.C
解:∵平行四边形的对角线互相平分,
∴矩形,菱形,正方形的对角线也必然互相平分.
故选:C.
2.D
解:因为正方形的一条对角线长为2,
设正方形的边长为,
根据勾股定理,得,
解得,
所以正方形的边长为,
则正方形的周长为.
故选:D.
3.C
解:根据正方形的性质得出∠EFG=∠EGH=∠HMG=90°,EG=GH,
∵∠FEG+∠EGF=90°,∠EGF+∠HGM=90°,
∴∠FEG=∠HGM,
在△EFG和△GMH中,
,
∴△EFG≌△GMH(AAS),
∴FG=MH,GM=EF,
∵A,C的边长分别为5和7,
∴EF2=52, HM2=72,
∴B的面积为EG2=EF2+FG2=EF2+HM2=25+49=74,
故答案为:C.
4.B
解:∵AC是正方形的对角线,
∴AC平分∠BCD,且∠BCD=90°,
∴∠ACD=∠ACB=45°,
∵∠DCE=∠BCD=90°,
∴∠ACE=∠ACD+∠DCE=45°+90°=135°,
∵AC=CE,
∴∠E=∠CAE=,
∴∠AFC=∠FDE+∠E=90°+22.5°=112.5°.
故选择B.
5.C
解:在正方形中,,,,
,
,
,
.
故选:C.
6.D
解:∵四边形ABCD是正方形,
∴∠ABC=90°,BC=BA,∠ABE=∠CBE=45°.
又BE=BE,
∴△ABE≌△CBE(SAS).
∴∠BAE=∠BCE=20°.
∵∠ABC=90°,∠BCF=20°
∴∠BFC=180°-∠ABC-∠BCF
=180°-90°-20°
=70°
∵∠BFC=∠BAE+∠AEF
∴∠AEF=∠BFC-∠BAE=70°-20°=50°
故选:D.
7.D
解:∵点A的坐标为(0,2),点B的坐标为(4,0),
∴OA=2,OB=4,
过D作DH⊥y轴于H,如图,
∵四边形ABCD是正方形,
∴AD=AB,∠DAB=90°,DE=BE,
∵∠AHD=∠AOB=90°,
∴∠DAH+∠AHD=∠AHD+∠BAO=90°,
∴∠ADH=∠BAO,
∴△ADH≌△BAO(AAS),
∴AH=OB=4,DH=OA=2,
∴OH=6,
∴D(2,6),
∵点E是BD的中点,点B的坐标为(4,0),
∴点E的坐标是(,),
∴E(3,3),
∵点F与点E关于y轴对称,
点F的坐标为(﹣3,3),
故选:D.
8.C
解:设,则,
四边形和四边形都是正方形,
,
,
即,解得或,
故选:C.
9.D
解:由题意知是的中位线
∴
∵正方形ABCD的周长为8
∴
∴
故选D.
10.A
解:如图,连接BB',连接BD,
∵四边形ABCD是正方形,且边长为2,
∴BD=AB=,BD平分∠ABC,
∵点E是AB的中点,
∴AE=BE=1,
∵四边形是正方形,
∴,平分∠ABC,
∴点B,点,点D三点共线,
∴.
故选:A.
11.B
解:在正方形中,对角线相等,所以正方形ABCD的对角线长均为6,
∵正方形又是菱形,菱形的面积计算公式是(a、b是正方形对角线长度)
∴,
故选:B.
12.C
解:设AB=x,AD=y,
∵长方形ABCD的周长是12cm,正方形ABEF和ADGH的面积之和为20 ,
∴x+y=6,,
∴,
∴,
∴,
故选C.
13.C
解:设CF与DE交于点O,
将△CDF沿CF折叠,点D落在点G处,
GO=DO, CF⊥DG,
四边形ABCD是正方形,
AD=CD,∠A=∠ADC=90°=∠FOD, ,
∠CFD+∠FCD=90°=∠CFD+∠ADE,
∠ADE=∠FCD,
在△ADE和△DCF中,
( ASA ),
AE=DF=5,
AE=5, AD=12,
DE=,
CF⊥DG, ,
,
,
DO==GO,
EG=
故答案为:C
14.D
解:∵正方形ABCD的对角线AC,BD交于点O,
∴OC=OD=BO=AO,∠ABO=∠ACB=45°,AC⊥BD.
∵∠MOB+∠BON=90°,∠BON+∠CON=90°
∴∠BOM=∠CON,且OC=OB,∠ABO=∠ACB=45°,
∴△BOM≌△CON(ASA),=S△BOM,
∴,
∵=S正方形ABCD,正方形的边长,,
∴=S正方形ABCD -=.
故选:D.
15.B
解:∵折痕为EF,
∴四边形EBCF与四边形EPGF全等
∴BE=PE,
故①正确;
如图2,作FK⊥AB于K.设EF交BP于O.
∵四边形ABCD为正方形,
∴AB=BC,∠A=∠ABC=∠C=90°,
∵FK⊥AB,
∴∠FKB=90°,
∴∠FKB=∠KBC=∠C=90°,
∴四边形BCFK是矩形,
∴KF=BC=AB,
∵EF为对称轴,点B与点P为对称点,
∴EF⊥PB,
∴∠BOE=90°,
∵∠ABP+∠BEO=90°,∠BEO+∠EFK=90°,
∴∠ABP=∠EFK,
在△ABP和△KFE中,
,
∴△ABP≌△KFE(ASA),
∴EF=BP,故②正确,
∵BE=PE,
∴∠EBP=∠EPB.
又∵∠EPH=∠EBC=90°,
∴∠EPH﹣∠EPB=∠EBC﹣∠EBP.
即∠PBC=∠BPH.
又∵AD∥BC,
∴∠APB=∠PBC.
∴∠APB=∠BPH.故③正确;
如图3,过B作BQ⊥PH,垂足为Q.
∴∠PQB=∠HQB=90°,
由(1)知∠APB=∠BPH,
在△APB和△QPB中,
,
∴△ABP≌△QBP(AAS),
∴AP=QP,AB=QB,
又∵AB=BC,
∴BC=BQ.
∵∠HQB=90°,∠C=90°
在Rt△BCH和Rt△BQH中
,
∴Rt△BCH≌Rt△BQH(HL),
∴CH=QH,
∴QP+QH=AP+CH,即PH=AP+CH,故④正确;
设EF与BP的交点为点N,如图4,
∵Rt△ABP≌Rt△QBP,△BCH≌△BQH,
∴∠ABP=∠QBP,∠CBH=∠QBH,
∴∠QBP+∠QBH=∠ABP+∠CBH,
即∠PBM=45°,
由折叠知,∠BPM=∠PBM=45°,∠EBM=∠EPM,∠PNF=∠BNF=90°,
∵AB∥CD,
∴∠MHF=∠EBM=∠EPM=45°+∠EPN,
∵在四边形DPNF中,∠D=∠PNF=90°,
∴∠MFH+∠DPN=180°,
∵∠DPN+∠APN=180°,
∴∠APN=∠MFH,
假设MH=MF,
∴∠MHF=∠MFH=∠APB,
在△ABP和△CBH中,
,
∴△ABP≌△CBH(AAS),
∴∠ABP=∠CBH,
∵∠ABP+∠CBH=45°,
∴∠ABP=∠CBH=22.5°,
∵点P在AD上,
∴0≤∠ABP≤45°,
∴∠ABP=22.5°与0≤∠ABP≤45°相矛盾,
∴假设不正确,故⑤错误.
故选:B.
16.135°
解:∵四边形ABCD是正方形,
∴∠CAD=45°,
∴∠OAC+∠OAD=45°,
又∵∠OAC=∠ODA,
∴∠ODA+∠OAD=45°,
∴∠AOD=180°-∠ODA-∠OAD=135°,
故答案为:135°.
17.6
解:连接CP,CE,
∵四边形ABCD是正方形,
∴AB=BC,∠ABD=∠CBP,
在△ABP和△CBP中,
,
∴△ABP≌△CBP(SAS),
∴AP=CP,
∴AP+PE最小值为CE的长,
∵AE=1,
∴BE=AB AE=3,
在Rt△CBE中,由勾股定理得:
CE=,
∴△PAE周长的最小值为CE+AE=5+1=6,
故答案为:6.
18.
解:∵四边形EFGH是正方形
∴GH=EF=2
∵△ABH≌△BCG
∴BG=AH=6
∴BH=BG+GH=6+2=8
∴
∵ △ABH、△BCG、△CDF和△DAE是四个全等的直角三角形
∴这四个直角三角形的面积均为24
∵四边形EFGH是正方形
∴
∴
故答案为:100
19.
解:由题意知,面积为的正方形的边长为1,
面积为的正方形的边长为,
面积为的正方形的边长为,
面积为的正方形的边长为,
……
推导一般性规律为:
∴
故答案为:.
20.13
解:解:如图,设CF与BD交于点Q,
∵∠ACB=90°,AC=4,BC=3
∴在Rt中,利用勾股定理得:
∵四边形ABDE是正方形,
∴∠ABQ=∠D=∠ACB=90°,AB=BD,
∴∠ABC+∠CAB=90°,∠ABC+∠PBD=90°,
∴∠PBD =∠CAB,
∴≌,
∴=,
∴-=-
即:=,
∴S阴=S正方形ABDE-2S△ABC==25-12=13,
故答案为13.
21.见解析
证明:∵正方形ABCD
∴BC=AB,∠ABC=90°,
∴∠EBF=∠ABC=90°,
∴∠ABF+∠FBC=∠CBE+∠FBC
∴∠ABF=∠CBE,
又∵BF=BE,
∴△ABF≌△CBE(SAS),
∴AF=CE.
22.见解析
证明:∵四边形ABCD是正方形,
∴AB=BC,∠ABE=∠BCF=90°,
又BE=CF,
∴△ABE≌△BCF(SAS).
∴∠BAE=∠CBF.
∵∠ABO+∠CBF=90°,
∴∠ABO+∠BAO=90°,即∠AOB=90°.
在Rt△ABO中,M点是斜边AB中点,
∴.
23.(1)见解析 (2)OD=AB,理由见解析
(1)
证明:在正方形ABCD中,∠ABC=∠C=90°,AB=BC,
∴∠BAE+∠AEB=90°,
∵BF⊥AE,
∴∠EOB=90°,
∴∠CBF+∠AEB=90°,
∴∠BAE=∠CBF,
∴△ABE≌△BCF,
∴BF=AE;
(2)
解:OD=AB,理由如下:
如图,延长AD交射线BM于点G,
由(1)得:△ABE≌△BCF,
∴BE=CF,
∵E是BC的中点,
∴,
∴CF=DF,
∵AD∥BC,
∴∠DGF=∠CBF,
在△DGF和△CBF中,
∵∠DGF=∠CBF,∠DFG=∠BFC,DF=CF,
∴△DGF≌△CBF,
∴DG=BC,
∴DG=AD,即OD为△AOG的中线,
∵BF⊥AE,
∴.
24.(1)见详解; (2)∠AFE=75°.
(1)
证明:∵四边形ABCD为正方形,
∴AB=DC,∠FAD=90°=∠CDA,
∵点E为DF中点.
∴AE=FE=DE,
∴∠EAD=∠EDA,
∴∠BAE-∠EAD=∠CDA-∠EDA,即∠BAE=∠CDE,
在△AEB和△DEC,
,
∴△AEB≌△DEC(SAS);
(2)
解:∵△AEB≌△DEC;
∴BE=CE,
∵EB=BC,
∴BC=BE=CE,
∴∠EBC=∠ECB=∠BEC=60°
∴∠EBF=90°-∠EBC=90°-60°=30°,∠ECD=90°-∠ECB=90°-60°=30°,
∵CE=BC=CD,
∴∠DEC=∠EDC=,
∴∠FEB=180°-∠BEC-∠CED=180°-60°-75°=45°,
∵∠AFE为△FBE的外角,
∴∠AFE=∠FBE+∠FEB=30°+45°=75°.
25.(1)证明见解析 (2)成立,理由见解析 (3)戓,理由见解析
(1)
解:∵四边形ABCD是正方形,
∴AB=BC,∠ABM=∠CBM,
在△ABM和△CBM中,
,
∴△ABM≌△CBM(SAS).
∴∠BAM=∠BCM,
又∵∠ECF=90°,G是EF的中点,
∴GC=EF=GF,
∴∠GCF=∠GFC,
又∵AB∥DF,
∴∠BAM=∠GFC,
∴∠BCM=∠GCF,
∴∠BCM+∠GCE=∠GCF+∠GCE=90°,
∴GC⊥CM;
(2)
解:成立;理由如下:
∵四边形ABCD是正方形,
∴AB=BC,∠ABM=∠CBM,
在△ABM和△CBM中,
,
∴△ABM≌△CBM(SAS),
∴∠BAM=∠BCM,
又∵∠ECF=90°,G是EF的中点,
∴GC=GF,
∴∠GCF=∠GFC,
又∵AB∥DF,
∴∠BAM=∠GFC,
∴∠BCM=∠GCF,
∴∠GCF+∠MCF=∠BCM+∠MCF=90°,
∴GC⊥CM;
(3)
解:分两种情况:①当点E在BC边上时,
∵∠MEC>90°,要使△MCE是等腰三角形,必须EM=EC,
∴∠EMC=∠ECM,
∴∠AEB=2∠BCM=2∠BAE,
∴2∠BAE+∠BAE=90°,
∴∠BAE=30°,
∴,
∵,
∴
∴;
②当点E在BC的延长线上时,同①知BE= .
综上①②,当BE=戓BE=时,△MCE是等腰三角形.
答案第1页,共2页
