2021-2022学年人教版八年级数学下册18.2.3正方形(判定)课时练习(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版八年级数学下册18.2.3正方形(判定)课时练习(Word版含答案) |

|
|
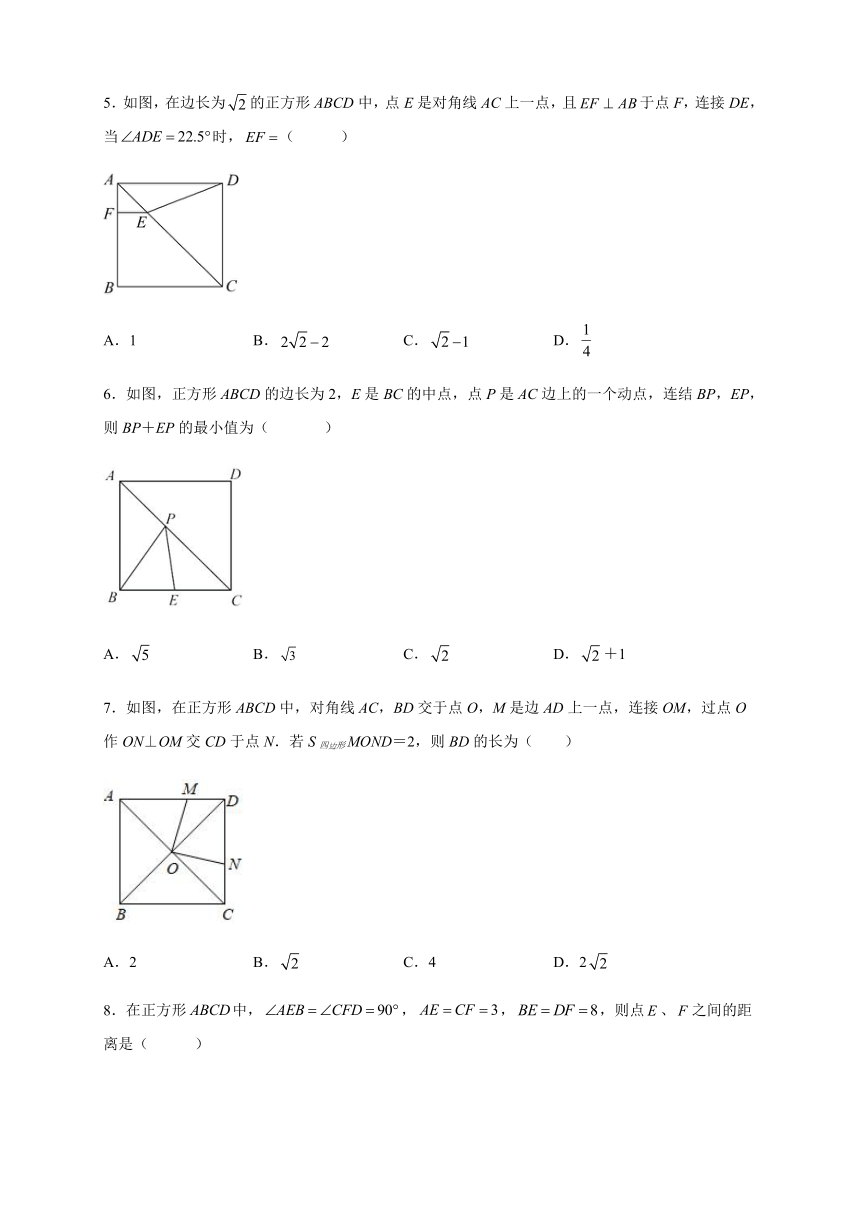
| 格式 | docx | ||
| 文件大小 | 897.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-21 12:11:51 | ||
图片预览


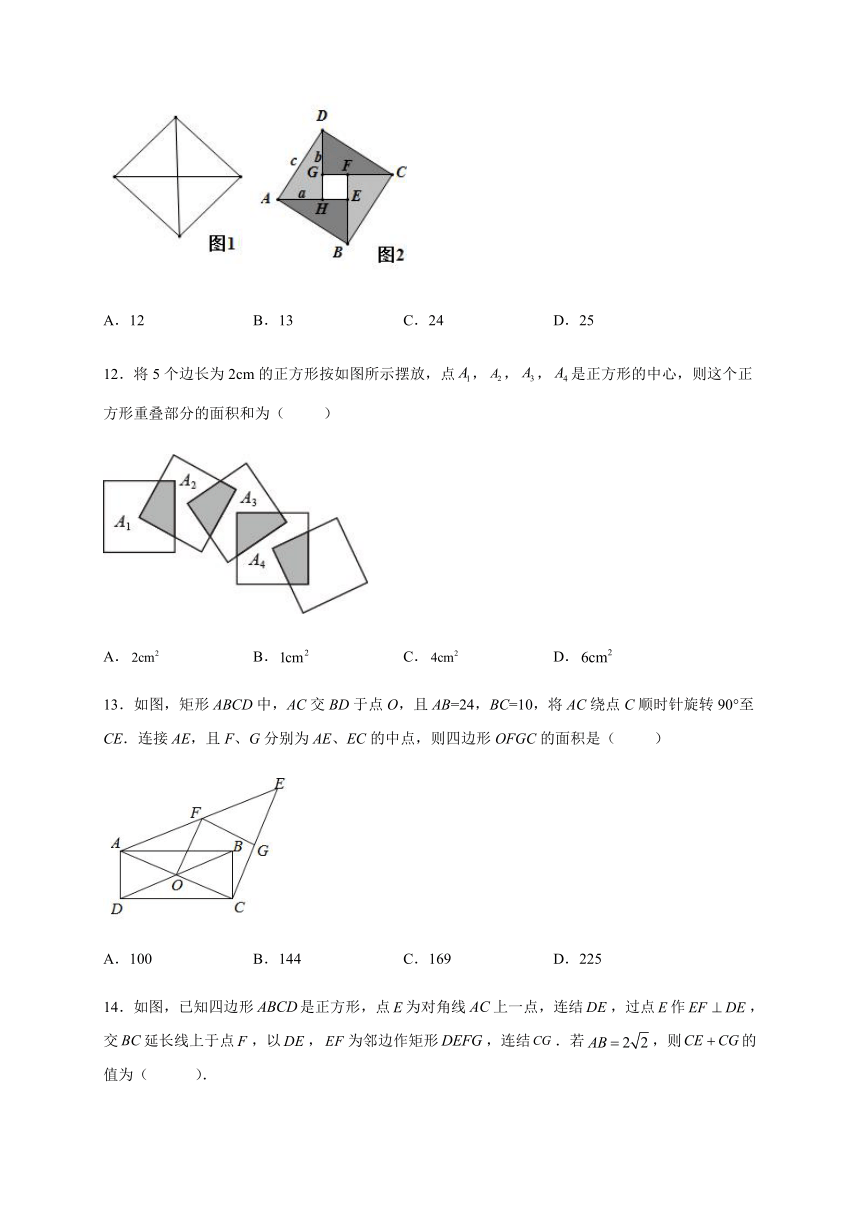
文档简介
正方形(判定)
一、单选题
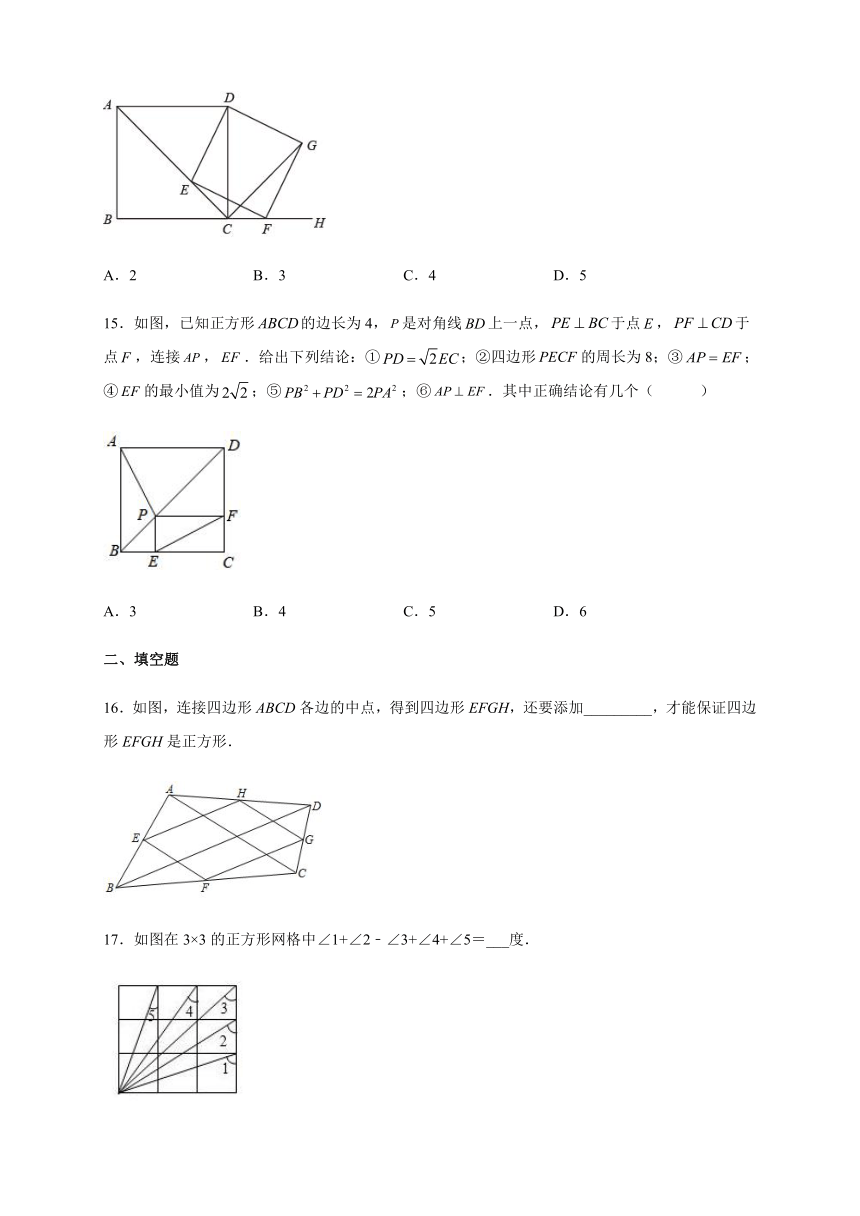
1.在四边形ABCD中,∠A=∠B=∠C=90°.如果再添加一个条件可推出四边形是正方形,那么这个条件可以是( )
A.AB=CD B.BC=CD C.∠D=90° D.AC=BD
2.如图,在矩形ABCD中,对角线AC,BD交于点O,下列条件:①AC⊥BD,②AB=BC,③∠ACB=45°,④OA=OB.上述条件能使矩形ABCD是正方形的是( )
A.①②③④ B.①②③ C.②③④ D.①③④
3.如图,在正方体的两个面上画了两条对角线、,则等于( )
A.135° B.90° C.75° D.60°
4.如图,在正方形ABCD中,以对角线BD为边作菱形BDFE,连接BF,则∠AFB=( )
A.22.5° B.25° C.30° D.不能确定
5.如图,在边长为的正方形ABCD中,点E是对角线AC上一点,且于点F,连接DE,当时,( )
A.1 B. C. D.
6.如图,正方形ABCD的边长为2,E是BC的中点,点P是AC边上的一个动点,连结BP,EP,则BP+EP的最小值为( )
A. B. C. D.+1
7.如图,在正方形ABCD中,对角线AC,BD交于点O,M是边AD上一点,连接OM,过点O作ON⊥OM交CD于点N.若S四边形MOND=2,则BD的长为( )
A.2 B. C.4 D.2
8.在正方形中,,,,则点、之间的距离是( )
A. B. C.5 D.6
9.如图,以RtABC的斜边AB为边,在AB的右侧作正方形ABDE,对角线AD,BE交于点O,已知,AC=10,BC=6,则OC的长为( )
A. B.8 C.12 D.
10.正方形与正方形按如图方式放置,点,,在同一直线上,已知,,连接并取中点,则的长为( )
A. B. C. D.
11.如图,将图1中的菱形纸片沿对角线剪成4个直角三角形,拼成如图2的四边形(相邻纸片之间不重叠,无缝隙).若四边形的面积为13,中间空白处的四边形的面积为1,直角三角形的两条直角边分别为和,则( )
A.12 B.13 C.24 D.25
12.将5个边长为2cm的正方形按如图所示摆放,点,,,是正方形的中心,则这个正方形重叠部分的面积和为( )
A. B. C. D.
13.如图,矩形ABCD中,AC交BD于点O,且AB=24,BC=10,将AC绕点C顺时针旋转90°至CE.连接AE,且F、G分别为AE、EC的中点,则四边形OFGC的面积是( )
A.100 B.144 C.169 D.225
14.如图,已知四边形是正方形,点为对角线上一点,连结,过点作,交延长线上于点,以,为邻边作矩形,连结.若,则的值为( ).
A.2 B.3 C.4 D.5
15.如图,已知正方形的边长为4,是对角线上一点,于点,于点,连接,.给出下列结论:①;②四边形的周长为8;③;④的最小值为;⑤;⑥.其中正确结论有几个( )
A.3 B.4 C.5 D.6
二、填空题
16.如图,连接四边形ABCD各边的中点,得到四边形EFGH,还要添加_________,才能保证四边形EFGH是正方形.
17.如图在3×3的正方形网格中∠1+∠2﹣∠3+∠4+∠5=___度.
18.如图,在正方形ABCD中,点M,N为CD,BC上的点,且DM=CN,AM与DN交于点P,连接AN,点Q为AN中点,连接PQ,若AB=10,DM=4,则PQ的长为 __________________.
19.如图,在正方形ABCD中,AB=4,点E,F分别在边AB,AD上,且AE=DF=1.连接CE,BF交于点G,则四边形CDFG(图中阴影部分)的面积是 __________________.
20.如图在正方形ABCD中,∠EAF的两边分别交CB、DC延长线于E、F点且∠EAF=45°,如果BE=1,DF=7,则EF=__.
三、解答题
21.如图,在正方形ABCD中,E是AD的中点,F是BA延长线上一点,AF=AB,求证:BE=FD.
22.如图,四边形ABCD是一个正方形,E、F分别在AD、DC边上,且DE=CF,AF、BE交于O点,请说出线段AF和BE的关系,并证明你的结论.
23.如图,E是正方形ABCD内一点,△BCE是等边三角形,连接DE,AE,延长DE交AB于点F
(1)求证:△ABE≌△DCE;
(2)求∠AED的度数
24.如图,正方形ABCD的对角线交于点O,点E是线段OD上一点,连接EC,作BF⊥CE于点F,交OC于点G.
(1)求证:BG=CE;
(2)若AB=4,BF是∠DBC的角平分线,求OG的长.
25.如图,E、F是正方形ABCD的边AD上的两个动点,满足AE=DF.连接CF交BD于G,连接BE交AG于H.已知正方形ABCD的边长为4cm,解决下列问题:
(1)求证:BE⊥AG;
(2)求线段DH的长度的最小值.
26.在正方形ABCD中,点E是CD边上任意一点.连接AE,过点B作BF⊥AE于F.交AD于H.
(1)如图1,过点D作DG⊥AE于G,求证:△AFB≌△DGA;
(2)如图2,点E为CD的中点,连接DF,求证:FH+FE=DF;
(3)如图3,AB=1,连接EH,点P为EH的中点,在点E从点D运动到点C的过程中,点P随之运动,请直接写出点P运动的路径长.
试卷第1页,共3页
参考答案:
1.B
解:∵∠A=∠B=∠C=90°,
∴四边形ABCD是矩形,
当BC=CD时,四边形ABCD是正方形,
故选:B.
2.B
解:①添加AC⊥BD,根据对角线互相垂直的矩形是正方形,故添加AC⊥BD,能使矩形ABCD成为正方形;
②添加AB=BC,根据有一组邻边相等的矩形是正方形,故添加AB=BC,能使矩形ABCD成为正方形;
③添加∠ACB=45°,
∵∠ABC=90°,
∴∠ACB=B∠AC=45°,
∴AB=BC,根据有一组邻边相等的矩形是正方形,故添加∠ACB=45°,能使矩形ABCD成为正方形;
④∵矩形ABCD中,
∴AC=BD,则AO=BO,故添加OA=OB,不能使矩形ABCD成为正方形;
综上,①②③符合题意,
故选:B.
3.D
解:连接BC,
∵AC、AB、BC是正方形的对角线,
∴AC=AB=BC,
∴△ABC为等边三角形.
∴∠BAC=60°.
故选D.
4.A
解:在正方形ABCD中,∠ADB=∠ADC=×90°=45°,
在菱形BDFE中,BD=DF,
所以,∠DBF=∠AFB,
在△BDF中,∠ADB=∠DBF+∠AFB=2∠AFB=45°,
解得∠AFB=22.5°.
故选:A.
5.C
解:四边形是正方形,
,,,
,
,
,
,
,
,
,
,
,
是等腰直角三角形,
,
故选:C.
6.A
解:连接BD,
∵正方形是轴对称图形,所在的直线是正方形的一条对称轴,
∴无论P在什么位置,都有PD=PB;
故均有BP+EP=PD+PE成立;
连接DE与AC,所得的交点,即为BP+EP的最小值时的位置,
如图所示:
此时BP+EP=DE,
∵正方形ABCD的边长为2,
∴DC=BC=2,
∵E是BC的中点,
∴EC=1,
在Rt△DEC中,
DE===,
故选:A.
7.C
解:∵四边形ABCD为正方形,
∴OD=OB=OC,∠COD=90°,∠OCD=∠ODA=45°,
∵ON⊥OM,
∴∠MON=90°,
∵∠CON+∠DON=90°,∠DOM+∠DON=90°,
∴∠CON=∠DOM,
在△OCN和△ODM中,
,
∴△OCN≌△ODM(ASA),
∴S△OCN=S△ODM,
∴S△OCN+S△DON=S△ODM+S△DON,
即S△ODC=S四边形MOND=2,
∵OD OC=2,
而OD=OC,
∴OD=2,
∴BD=2OD=4.
故选:C.
8.A
解:如图所示:
四边形是正方形,
,,
,
在和中,
,
,
,
,
,
,
同理:,
,
即,
同理:,
在和中,
,
,
,,
同理:,,
,
,
四边形是正方形,
;
故选:A.
9.B
解:过点O作OM垂直于CA于点M,作ON垂直于CB的延长线于点N,
∴∠OMC=∠ONC=90°,
∵∠ACB=90°
∴四边形MCNO是矩形,
∴∠MON=90°,
∵正方形ABDE对角线交于点O,
∴OA=OB,∠AOB=90°,
∴∠MON-∠AON=∠AOB-∠AON,
∴∠AOM=∠NOB,
∵∠OMA=∠ONB=90°,
在△AOM和△BON中,
,
∴△AOM≌△BON(AAS),
∴OM=ON,AM=BN,
∴矩形MCNO是正方形,
∴∠ACO=∠BCO=45°,CM=CN=ON
∵AC=10,BC=6,
∴CN=CM=,
由勾股定理得:OC=8.
故选:B.
10.A
解:延长AM交BC于H点,∵四边形与四边形都是正方形,,,
∴BF=,AB=AD=CD=BC=3,
∵点,,在同一直线上,
∴ADCF
∴∠DAM=∠FHM,∠ADM=∠HFM,
又是DF中点,DM=FM
∴△ADM≌△HFM
∴AD=FH=3,AM=HM=AH
∴BH=FH-BF=1
在Rt△ABH中,AH=
∴AM=AH=
故选A.
11.D
解:菱形的对角线互相垂直平分,
个直角三角形全等;
,,
,
四边形是正方形,又正方形的面积为13,
正方形的边长为,
根据勾股定理,则,
中间空白处的四边形的面积为1,
个直角三角形的面积为,
,
,
,
.
故选D.
12.C
解:如图,连接AP,AN,点A是正方形的对角线的交
则AP=AN,∠APF=∠ANE=45°,
∵∠PAF+∠FAN=∠FAN+∠NAE=90°,
∴∠PAF=∠NAE,
∴△PAF≌△NAE,
∴四边形AENF的面积等于△NAP的面积,
而△NAP的面积是正方形的面积的,而正方形的面积为4,
∴四边形AENF的面积为1cm2,四块阴影面积的和为4cm2.
故选C.
13.C
解:四边形为矩形,,
,
分别为的中点,
,
,
四边形为平行四边形,
又绕点顺时针旋转,
,
,
平行四边形为正方形,
四边形的面积是,
故选:C.
14.C
解:如图,作EK⊥BC于点K,EP⊥DC于点P,
∵四边形ABCD为正方形,AC为对角线,
∴,,
∵,,
∴,
在与中,
,
∴,
∴,
∴矩形DEFG为正方形,
∵,,
∴,
在与中,
,
∴,
∴,
∴,
∵,
∴,
∴,
故选:C.
15.D
解:如图,过点作于点,连接,
由题意知
∴四边形为平行四边形
∵
∴四边形为矩形
∴
∵
∴
∵
∴
∴是等腰直角三角形
∴
①∵,
∴为等腰直角三角形
∴
,
∴
∴四边形是平行四边形
∴
∴
故①正确;
②∵
∴四边形为矩形
∴四边形的周长
故②正确;
③四边形为矩形
∵在和中
∵
∴
∴
∴
故③正确;
④∵
当最小时,最小
∴当时,即时,的最小值等于
故④正确;
⑤在和中,,
∴
故⑤正确;
⑥如图1,延长与交于点
∵在和中
∵
∴
∴
∵
∴
∴
故⑥正确;
综上,①②③④⑤⑥正确,
故选:.
16.AC⊥BD,AC=BD## AC=BD, AC⊥BD
解:当AC⊥BD,AC=BD时,四边形EFGH为正方形.
∵点E、F、G、H分别为AB、BC、CD、DA的中点,
∴EF∥AC,EF=AC,GH∥AC,GH=AC,EH∥BD,EH=BD,
∴EF∥GH,EF=GH,
∴四边形EFGH为平行四边形,
当AC⊥BD,AC=BD时,EF⊥EH,EF=EH,
∴四边形EFGH为正方形.
故答案为:AC⊥BD,AC=BD.
17.135°
解:观察图形可知∠1与∠5所在的三角形全等,二角互余,∠2与∠4所在的三角形全等,二角互余,∠3=45°
∴∠1+∠5=90°,∠2+∠4=90°,∠3=45°,
∴∠1+∠2-∠3+∠4+∠5=(∠1+∠5)+(∠2+∠4)-∠3=135°.
故答案为:135°.
18.
解:在正方形ABCD中,
AD=CD,∠ADC=∠DCN=90°,
在△ADM与△DCN中,
∵AD=CD,DM=CN,∠ADC=∠DCN,
∴△ADM≌△DCN(SAS),
∴∠DAM=∠CDN,
∴∠DMA=∠CND,
在△DPM中,∠PDM+∠PMD=90°,
∴∠DPM=90°,
∵∠DPM=∠APN,
∴△ANP为直角三角形,
AN为直角三角形的斜边,由直角三角形的性质得PQ=AN,
在△ANB中,AN==2,
∴PQ=,
故答案为:.
19.
解:连接,
四边形是正方形,
,,
,
,
,
在和中,
,
,
,
,
,
,
,
,
,
,
.
故答案为:.
20.6
解:如图,把△ABE绕点A逆时针旋转90°到DA,交CD于点G,
由旋转的性质可知,AG=AE,DG=BE,∠DAG=∠BAE,
∵∠EAF=45°,
∴∠DAG+∠BAF=45°,
又∵∠BAD=90°,
∴∠GAF=45°,
在△AEF和△AGF中,
,
∴△AEF≌△AGF(SAS)
∴EF=GF,
∵BE=1,DF=7,
∴EF=GF=DF﹣DG=DF﹣BE=7﹣1=6.
故答案为:6.
21.见解析
证明:∵E是AD的中点,
∴AE=AD,
∵AF=AB,
∵正方形ABCD,
∴AB=AD,∠DAB=∠DAF=90°,
∴AF=AE,
∴Rt△ADF≌Rt△ABE(SAS),
∴BE=DF.
22.AF=BE,AF⊥BE,证明见解析.
解:AF⊥BE,AF=BE,证明如下:
∵正方形ABCD
∴AB=AD=DC,∠D=∠BAD=90°
∵CF=DE
∴AE=AD-DE,DF=DC-CF
∴AE=DF
在△AEB和△AFD中
AB=AD, ∠D=∠BAD, AE=DF
∴△ABE≌△DAF(SAS)
∴∠ABE=∠FAD,AF=BE
∵∠BAD=90°
∴∠ABE+∠AEB=90°
∴∠FAD +∠AEB=90°
∴∠AOE=90°,AF⊥BE.
∴AF=BE,AF⊥BE.
23.(1)见解析;(2)150°
(1)证明:在正方形ABCD中,AB=DC,∠ABC=∠BCD=90°,
∵ △BCE为等边三角形,
∴ BE=CE,∠EBC=∠ECB=60°,
∴ ∠ABC-∠EBC=∠BCD-∠ECB ,
即:∠ABE=∠DCE=30° ,
在△ABE和△DCE中, ,
∴ △ABE≌△DCE,
(2)在正方形ABCD中,∠BAD=∠ADC=90°,BC=CD,
∵ △BCE为等边三角形,
∴ CE=BC, ,
∵ ,
∴ ,
∴△CDE为等腰三角形, ,
由(1)得:∠DCE=30°,
∴ ,
由(1)得:△ABE≌△DCE,
∴ ,
∴△ADE为等腰三角形,
∴ ,
∴ ,
24.(1)见解析;(2).
(1)证明:正方形中,、相交于,
,,
,
,
,
,
,
.
(2)解:是的角平分线,
,
,,
,
,
在中,,
解得:,
,
,
.
25.(1)见解析;(2)2-2..
(1)证明:在正方形ABCD中,AB=AD=CD,∠BAD=∠CDA,∠ADG=∠CDG,
在△ABE和△DCF中,
,
∴△ABE≌△DCF(SAS),
∴∠1=∠2,
在△ADG和△CDG中,
,
∴△ADG≌△CDG(SAS),
∴∠2=∠3,
∴∠1=∠3,
∵∠BAH+∠3=∠BAD=90°,
∴∠1+∠BAH=90°,
∴∠AHB=180°-90°=90°,
∴BE⊥AG;
(2)解:如图,取AB的中点O,连接OH、OD,
则OH=AO=AB=2,
在Rt△AOD中,OD=,
根据三角形的三边关系,OH+DH>OD,
∴当O、D、H三点共线时,DH的长度最小,
DH的最小值=OD-OH=2-2.
26.(1)证明见解析 (2)证明见解析 (3)
(1)
证明:∵四边形ABCD是正方形,
∴AB=AD,∠BAD=90°
∵DG⊥AE,BF⊥AE
∴∠AFB=∠DGA=90°
∵∠FAB+∠DAG=90°,∠DAG+∠ADG=90°
∴∠BAF=∠ADG
在△AFB和△DGA中
∵
∴△AFB≌△DGA(AAS).
(2)
证明:如图2,过点D作DK⊥AE于K,DJ⊥BF交BF的延长线于J
由题意知∠BAH=∠ADE=90°,AB=AD=CD
∵BF⊥AE
∴∠AFB=90°
∵∠DAE+∠EAB=90°,∠EAB+∠ABH=90°
∴∠DAE=∠ABH
在△ABH和△DAE中
∵
∴△ABH≌△DAE(ASA)
∴AH=DE
∵点E为CD的中点
∴DE=EC= CD
∴AH=DH
∴DE=DH
∵DJ⊥BJ,DK⊥AE
∴∠J=∠DKE=∠KFJ=90°
∴四边形DKFJ是矩形
∴∠JDK=∠ADC=90°
∴∠JDH=∠KDE
在△DJH和△DKE中
∵
∴△DJH≌△DKE(AAS)
∴DJ=DK,JH=EK
∴四边形DKFJ是正方形
∴FK=FJ=DK=DJ
∴DF=FJ
∴
∴FH+FE=FJ﹣HJ+FK+KE=2FJ=DF.
(3)
解:如图3,取AD的中点Q,连接PQ,延长QP交CD于R,过点P作PT⊥CD于T,PK⊥AD于K,设PT=b
由(2)得△ABH≌△DAE(ASA)
∴AH=DE
∵∠EDH=90°,点P为EH的中点
∴PD=EH=PH=PE
∵PK⊥DH,PT⊥DE
∴∠PKD=∠KDT=∠PTD=90°
∴四边形PTDK是矩形
∴PT=DK=b,PK=DT
∵PH=PD=PE,PK⊥DH,PT⊥DE
∴PT是△DEH的中位线
∴DH=2DK=2b,DE=2DT
∴AH=DE=1﹣2b
∴PK= DE=﹣b,QK=DQ﹣DK=﹣b
∴PK=QK
∵∠PKQ=90°
∴△PKQ是等腰直角三角形
∴∠KQP=45°
∴点P在线段QR上运动,△DQR是等腰直角三角形
∴QR=DQ=
∴点P的运动轨迹的长为.
答案第1页,共2页
一、单选题
1.在四边形ABCD中,∠A=∠B=∠C=90°.如果再添加一个条件可推出四边形是正方形,那么这个条件可以是( )
A.AB=CD B.BC=CD C.∠D=90° D.AC=BD
2.如图,在矩形ABCD中,对角线AC,BD交于点O,下列条件:①AC⊥BD,②AB=BC,③∠ACB=45°,④OA=OB.上述条件能使矩形ABCD是正方形的是( )
A.①②③④ B.①②③ C.②③④ D.①③④
3.如图,在正方体的两个面上画了两条对角线、,则等于( )
A.135° B.90° C.75° D.60°
4.如图,在正方形ABCD中,以对角线BD为边作菱形BDFE,连接BF,则∠AFB=( )
A.22.5° B.25° C.30° D.不能确定
5.如图,在边长为的正方形ABCD中,点E是对角线AC上一点,且于点F,连接DE,当时,( )
A.1 B. C. D.
6.如图,正方形ABCD的边长为2,E是BC的中点,点P是AC边上的一个动点,连结BP,EP,则BP+EP的最小值为( )
A. B. C. D.+1
7.如图,在正方形ABCD中,对角线AC,BD交于点O,M是边AD上一点,连接OM,过点O作ON⊥OM交CD于点N.若S四边形MOND=2,则BD的长为( )
A.2 B. C.4 D.2
8.在正方形中,,,,则点、之间的距离是( )
A. B. C.5 D.6
9.如图,以RtABC的斜边AB为边,在AB的右侧作正方形ABDE,对角线AD,BE交于点O,已知,AC=10,BC=6,则OC的长为( )
A. B.8 C.12 D.
10.正方形与正方形按如图方式放置,点,,在同一直线上,已知,,连接并取中点,则的长为( )
A. B. C. D.
11.如图,将图1中的菱形纸片沿对角线剪成4个直角三角形,拼成如图2的四边形(相邻纸片之间不重叠,无缝隙).若四边形的面积为13,中间空白处的四边形的面积为1,直角三角形的两条直角边分别为和,则( )
A.12 B.13 C.24 D.25
12.将5个边长为2cm的正方形按如图所示摆放,点,,,是正方形的中心,则这个正方形重叠部分的面积和为( )
A. B. C. D.
13.如图,矩形ABCD中,AC交BD于点O,且AB=24,BC=10,将AC绕点C顺时针旋转90°至CE.连接AE,且F、G分别为AE、EC的中点,则四边形OFGC的面积是( )
A.100 B.144 C.169 D.225
14.如图,已知四边形是正方形,点为对角线上一点,连结,过点作,交延长线上于点,以,为邻边作矩形,连结.若,则的值为( ).
A.2 B.3 C.4 D.5
15.如图,已知正方形的边长为4,是对角线上一点,于点,于点,连接,.给出下列结论:①;②四边形的周长为8;③;④的最小值为;⑤;⑥.其中正确结论有几个( )
A.3 B.4 C.5 D.6
二、填空题
16.如图,连接四边形ABCD各边的中点,得到四边形EFGH,还要添加_________,才能保证四边形EFGH是正方形.
17.如图在3×3的正方形网格中∠1+∠2﹣∠3+∠4+∠5=___度.
18.如图,在正方形ABCD中,点M,N为CD,BC上的点,且DM=CN,AM与DN交于点P,连接AN,点Q为AN中点,连接PQ,若AB=10,DM=4,则PQ的长为 __________________.
19.如图,在正方形ABCD中,AB=4,点E,F分别在边AB,AD上,且AE=DF=1.连接CE,BF交于点G,则四边形CDFG(图中阴影部分)的面积是 __________________.
20.如图在正方形ABCD中,∠EAF的两边分别交CB、DC延长线于E、F点且∠EAF=45°,如果BE=1,DF=7,则EF=__.
三、解答题
21.如图,在正方形ABCD中,E是AD的中点,F是BA延长线上一点,AF=AB,求证:BE=FD.
22.如图,四边形ABCD是一个正方形,E、F分别在AD、DC边上,且DE=CF,AF、BE交于O点,请说出线段AF和BE的关系,并证明你的结论.
23.如图,E是正方形ABCD内一点,△BCE是等边三角形,连接DE,AE,延长DE交AB于点F
(1)求证:△ABE≌△DCE;
(2)求∠AED的度数
24.如图,正方形ABCD的对角线交于点O,点E是线段OD上一点,连接EC,作BF⊥CE于点F,交OC于点G.
(1)求证:BG=CE;
(2)若AB=4,BF是∠DBC的角平分线,求OG的长.
25.如图,E、F是正方形ABCD的边AD上的两个动点,满足AE=DF.连接CF交BD于G,连接BE交AG于H.已知正方形ABCD的边长为4cm,解决下列问题:
(1)求证:BE⊥AG;
(2)求线段DH的长度的最小值.
26.在正方形ABCD中,点E是CD边上任意一点.连接AE,过点B作BF⊥AE于F.交AD于H.
(1)如图1,过点D作DG⊥AE于G,求证:△AFB≌△DGA;
(2)如图2,点E为CD的中点,连接DF,求证:FH+FE=DF;
(3)如图3,AB=1,连接EH,点P为EH的中点,在点E从点D运动到点C的过程中,点P随之运动,请直接写出点P运动的路径长.
试卷第1页,共3页
参考答案:
1.B
解:∵∠A=∠B=∠C=90°,
∴四边形ABCD是矩形,
当BC=CD时,四边形ABCD是正方形,
故选:B.
2.B
解:①添加AC⊥BD,根据对角线互相垂直的矩形是正方形,故添加AC⊥BD,能使矩形ABCD成为正方形;
②添加AB=BC,根据有一组邻边相等的矩形是正方形,故添加AB=BC,能使矩形ABCD成为正方形;
③添加∠ACB=45°,
∵∠ABC=90°,
∴∠ACB=B∠AC=45°,
∴AB=BC,根据有一组邻边相等的矩形是正方形,故添加∠ACB=45°,能使矩形ABCD成为正方形;
④∵矩形ABCD中,
∴AC=BD,则AO=BO,故添加OA=OB,不能使矩形ABCD成为正方形;
综上,①②③符合题意,
故选:B.
3.D
解:连接BC,
∵AC、AB、BC是正方形的对角线,
∴AC=AB=BC,
∴△ABC为等边三角形.
∴∠BAC=60°.
故选D.
4.A
解:在正方形ABCD中,∠ADB=∠ADC=×90°=45°,
在菱形BDFE中,BD=DF,
所以,∠DBF=∠AFB,
在△BDF中,∠ADB=∠DBF+∠AFB=2∠AFB=45°,
解得∠AFB=22.5°.
故选:A.
5.C
解:四边形是正方形,
,,,
,
,
,
,
,
,
,
,
,
是等腰直角三角形,
,
故选:C.
6.A
解:连接BD,
∵正方形是轴对称图形,所在的直线是正方形的一条对称轴,
∴无论P在什么位置,都有PD=PB;
故均有BP+EP=PD+PE成立;
连接DE与AC,所得的交点,即为BP+EP的最小值时的位置,
如图所示:
此时BP+EP=DE,
∵正方形ABCD的边长为2,
∴DC=BC=2,
∵E是BC的中点,
∴EC=1,
在Rt△DEC中,
DE===,
故选:A.
7.C
解:∵四边形ABCD为正方形,
∴OD=OB=OC,∠COD=90°,∠OCD=∠ODA=45°,
∵ON⊥OM,
∴∠MON=90°,
∵∠CON+∠DON=90°,∠DOM+∠DON=90°,
∴∠CON=∠DOM,
在△OCN和△ODM中,
,
∴△OCN≌△ODM(ASA),
∴S△OCN=S△ODM,
∴S△OCN+S△DON=S△ODM+S△DON,
即S△ODC=S四边形MOND=2,
∵OD OC=2,
而OD=OC,
∴OD=2,
∴BD=2OD=4.
故选:C.
8.A
解:如图所示:
四边形是正方形,
,,
,
在和中,
,
,
,
,
,
,
同理:,
,
即,
同理:,
在和中,
,
,
,,
同理:,,
,
,
四边形是正方形,
;
故选:A.
9.B
解:过点O作OM垂直于CA于点M,作ON垂直于CB的延长线于点N,
∴∠OMC=∠ONC=90°,
∵∠ACB=90°
∴四边形MCNO是矩形,
∴∠MON=90°,
∵正方形ABDE对角线交于点O,
∴OA=OB,∠AOB=90°,
∴∠MON-∠AON=∠AOB-∠AON,
∴∠AOM=∠NOB,
∵∠OMA=∠ONB=90°,
在△AOM和△BON中,
,
∴△AOM≌△BON(AAS),
∴OM=ON,AM=BN,
∴矩形MCNO是正方形,
∴∠ACO=∠BCO=45°,CM=CN=ON
∵AC=10,BC=6,
∴CN=CM=,
由勾股定理得:OC=8.
故选:B.
10.A
解:延长AM交BC于H点,∵四边形与四边形都是正方形,,,
∴BF=,AB=AD=CD=BC=3,
∵点,,在同一直线上,
∴ADCF
∴∠DAM=∠FHM,∠ADM=∠HFM,
又是DF中点,DM=FM
∴△ADM≌△HFM
∴AD=FH=3,AM=HM=AH
∴BH=FH-BF=1
在Rt△ABH中,AH=
∴AM=AH=
故选A.
11.D
解:菱形的对角线互相垂直平分,
个直角三角形全等;
,,
,
四边形是正方形,又正方形的面积为13,
正方形的边长为,
根据勾股定理,则,
中间空白处的四边形的面积为1,
个直角三角形的面积为,
,
,
,
.
故选D.
12.C
解:如图,连接AP,AN,点A是正方形的对角线的交
则AP=AN,∠APF=∠ANE=45°,
∵∠PAF+∠FAN=∠FAN+∠NAE=90°,
∴∠PAF=∠NAE,
∴△PAF≌△NAE,
∴四边形AENF的面积等于△NAP的面积,
而△NAP的面积是正方形的面积的,而正方形的面积为4,
∴四边形AENF的面积为1cm2,四块阴影面积的和为4cm2.
故选C.
13.C
解:四边形为矩形,,
,
分别为的中点,
,
,
四边形为平行四边形,
又绕点顺时针旋转,
,
,
平行四边形为正方形,
四边形的面积是,
故选:C.
14.C
解:如图,作EK⊥BC于点K,EP⊥DC于点P,
∵四边形ABCD为正方形,AC为对角线,
∴,,
∵,,
∴,
在与中,
,
∴,
∴,
∴矩形DEFG为正方形,
∵,,
∴,
在与中,
,
∴,
∴,
∴,
∵,
∴,
∴,
故选:C.
15.D
解:如图,过点作于点,连接,
由题意知
∴四边形为平行四边形
∵
∴四边形为矩形
∴
∵
∴
∵
∴
∴是等腰直角三角形
∴
①∵,
∴为等腰直角三角形
∴
,
∴
∴四边形是平行四边形
∴
∴
故①正确;
②∵
∴四边形为矩形
∴四边形的周长
故②正确;
③四边形为矩形
∵在和中
∵
∴
∴
∴
故③正确;
④∵
当最小时,最小
∴当时,即时,的最小值等于
故④正确;
⑤在和中,,
∴
故⑤正确;
⑥如图1,延长与交于点
∵在和中
∵
∴
∴
∵
∴
∴
故⑥正确;
综上,①②③④⑤⑥正确,
故选:.
16.AC⊥BD,AC=BD## AC=BD, AC⊥BD
解:当AC⊥BD,AC=BD时,四边形EFGH为正方形.
∵点E、F、G、H分别为AB、BC、CD、DA的中点,
∴EF∥AC,EF=AC,GH∥AC,GH=AC,EH∥BD,EH=BD,
∴EF∥GH,EF=GH,
∴四边形EFGH为平行四边形,
当AC⊥BD,AC=BD时,EF⊥EH,EF=EH,
∴四边形EFGH为正方形.
故答案为:AC⊥BD,AC=BD.
17.135°
解:观察图形可知∠1与∠5所在的三角形全等,二角互余,∠2与∠4所在的三角形全等,二角互余,∠3=45°
∴∠1+∠5=90°,∠2+∠4=90°,∠3=45°,
∴∠1+∠2-∠3+∠4+∠5=(∠1+∠5)+(∠2+∠4)-∠3=135°.
故答案为:135°.
18.
解:在正方形ABCD中,
AD=CD,∠ADC=∠DCN=90°,
在△ADM与△DCN中,
∵AD=CD,DM=CN,∠ADC=∠DCN,
∴△ADM≌△DCN(SAS),
∴∠DAM=∠CDN,
∴∠DMA=∠CND,
在△DPM中,∠PDM+∠PMD=90°,
∴∠DPM=90°,
∵∠DPM=∠APN,
∴△ANP为直角三角形,
AN为直角三角形的斜边,由直角三角形的性质得PQ=AN,
在△ANB中,AN==2,
∴PQ=,
故答案为:.
19.
解:连接,
四边形是正方形,
,,
,
,
,
在和中,
,
,
,
,
,
,
,
,
,
,
.
故答案为:.
20.6
解:如图,把△ABE绕点A逆时针旋转90°到DA,交CD于点G,
由旋转的性质可知,AG=AE,DG=BE,∠DAG=∠BAE,
∵∠EAF=45°,
∴∠DAG+∠BAF=45°,
又∵∠BAD=90°,
∴∠GAF=45°,
在△AEF和△AGF中,
,
∴△AEF≌△AGF(SAS)
∴EF=GF,
∵BE=1,DF=7,
∴EF=GF=DF﹣DG=DF﹣BE=7﹣1=6.
故答案为:6.
21.见解析
证明:∵E是AD的中点,
∴AE=AD,
∵AF=AB,
∵正方形ABCD,
∴AB=AD,∠DAB=∠DAF=90°,
∴AF=AE,
∴Rt△ADF≌Rt△ABE(SAS),
∴BE=DF.
22.AF=BE,AF⊥BE,证明见解析.
解:AF⊥BE,AF=BE,证明如下:
∵正方形ABCD
∴AB=AD=DC,∠D=∠BAD=90°
∵CF=DE
∴AE=AD-DE,DF=DC-CF
∴AE=DF
在△AEB和△AFD中
AB=AD, ∠D=∠BAD, AE=DF
∴△ABE≌△DAF(SAS)
∴∠ABE=∠FAD,AF=BE
∵∠BAD=90°
∴∠ABE+∠AEB=90°
∴∠FAD +∠AEB=90°
∴∠AOE=90°,AF⊥BE.
∴AF=BE,AF⊥BE.
23.(1)见解析;(2)150°
(1)证明:在正方形ABCD中,AB=DC,∠ABC=∠BCD=90°,
∵ △BCE为等边三角形,
∴ BE=CE,∠EBC=∠ECB=60°,
∴ ∠ABC-∠EBC=∠BCD-∠ECB ,
即:∠ABE=∠DCE=30° ,
在△ABE和△DCE中, ,
∴ △ABE≌△DCE,
(2)在正方形ABCD中,∠BAD=∠ADC=90°,BC=CD,
∵ △BCE为等边三角形,
∴ CE=BC, ,
∵ ,
∴ ,
∴△CDE为等腰三角形, ,
由(1)得:∠DCE=30°,
∴ ,
由(1)得:△ABE≌△DCE,
∴ ,
∴△ADE为等腰三角形,
∴ ,
∴ ,
24.(1)见解析;(2).
(1)证明:正方形中,、相交于,
,,
,
,
,
,
,
.
(2)解:是的角平分线,
,
,,
,
,
在中,,
解得:,
,
,
.
25.(1)见解析;(2)2-2..
(1)证明:在正方形ABCD中,AB=AD=CD,∠BAD=∠CDA,∠ADG=∠CDG,
在△ABE和△DCF中,
,
∴△ABE≌△DCF(SAS),
∴∠1=∠2,
在△ADG和△CDG中,
,
∴△ADG≌△CDG(SAS),
∴∠2=∠3,
∴∠1=∠3,
∵∠BAH+∠3=∠BAD=90°,
∴∠1+∠BAH=90°,
∴∠AHB=180°-90°=90°,
∴BE⊥AG;
(2)解:如图,取AB的中点O,连接OH、OD,
则OH=AO=AB=2,
在Rt△AOD中,OD=,
根据三角形的三边关系,OH+DH>OD,
∴当O、D、H三点共线时,DH的长度最小,
DH的最小值=OD-OH=2-2.
26.(1)证明见解析 (2)证明见解析 (3)
(1)
证明:∵四边形ABCD是正方形,
∴AB=AD,∠BAD=90°
∵DG⊥AE,BF⊥AE
∴∠AFB=∠DGA=90°
∵∠FAB+∠DAG=90°,∠DAG+∠ADG=90°
∴∠BAF=∠ADG
在△AFB和△DGA中
∵
∴△AFB≌△DGA(AAS).
(2)
证明:如图2,过点D作DK⊥AE于K,DJ⊥BF交BF的延长线于J
由题意知∠BAH=∠ADE=90°,AB=AD=CD
∵BF⊥AE
∴∠AFB=90°
∵∠DAE+∠EAB=90°,∠EAB+∠ABH=90°
∴∠DAE=∠ABH
在△ABH和△DAE中
∵
∴△ABH≌△DAE(ASA)
∴AH=DE
∵点E为CD的中点
∴DE=EC= CD
∴AH=DH
∴DE=DH
∵DJ⊥BJ,DK⊥AE
∴∠J=∠DKE=∠KFJ=90°
∴四边形DKFJ是矩形
∴∠JDK=∠ADC=90°
∴∠JDH=∠KDE
在△DJH和△DKE中
∵
∴△DJH≌△DKE(AAS)
∴DJ=DK,JH=EK
∴四边形DKFJ是正方形
∴FK=FJ=DK=DJ
∴DF=FJ
∴
∴FH+FE=FJ﹣HJ+FK+KE=2FJ=DF.
(3)
解:如图3,取AD的中点Q,连接PQ,延长QP交CD于R,过点P作PT⊥CD于T,PK⊥AD于K,设PT=b
由(2)得△ABH≌△DAE(ASA)
∴AH=DE
∵∠EDH=90°,点P为EH的中点
∴PD=EH=PH=PE
∵PK⊥DH,PT⊥DE
∴∠PKD=∠KDT=∠PTD=90°
∴四边形PTDK是矩形
∴PT=DK=b,PK=DT
∵PH=PD=PE,PK⊥DH,PT⊥DE
∴PT是△DEH的中位线
∴DH=2DK=2b,DE=2DT
∴AH=DE=1﹣2b
∴PK= DE=﹣b,QK=DQ﹣DK=﹣b
∴PK=QK
∵∠PKQ=90°
∴△PKQ是等腰直角三角形
∴∠KQP=45°
∴点P在线段QR上运动,△DQR是等腰直角三角形
∴QR=DQ=
∴点P的运动轨迹的长为.
答案第1页,共2页
