15.1.3 积的乘方
图片预览







文档简介
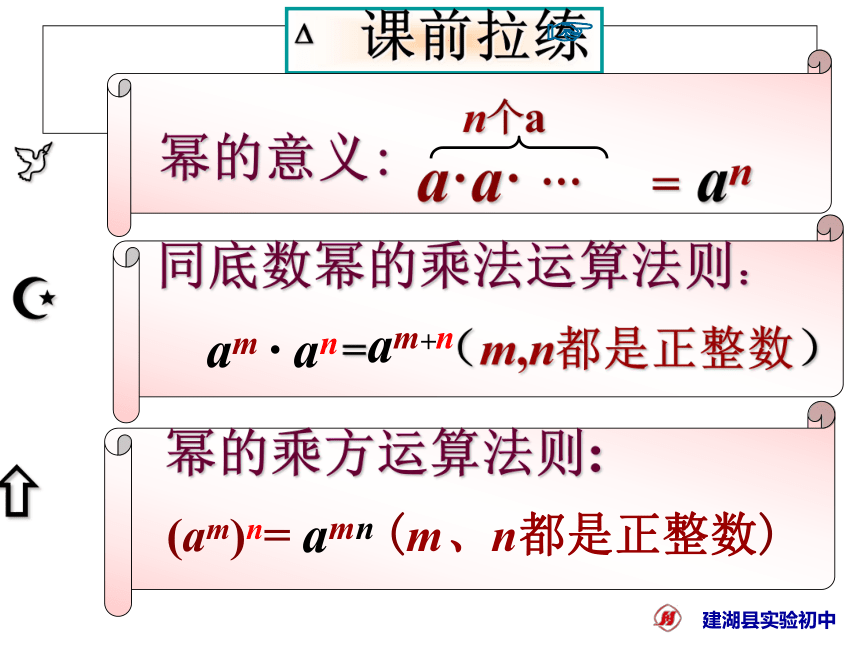
课件26张PPT。积的乘方鸡西市第十九中学 初三备课组回顾与思考?幂的意义:an=am+n(m,n都是正整数)(am)n= (m、n都是正整数)amn课前拉练:(1)27×24 (2) x3 ? x4 (3)103×104×105 (4) y ? y5 ? y2 (5)- t7·t; (6) –y2·y8; (7) a2m·am+2.(8) (106)3 (9) (ya)3 (10) -(m2)4 (11) (-2b)3 (12) (xy2)31.使学生经历探索积的乘方的过程,掌握积的乘方的运算法则。
2.能利用积的乘方的运算法则进行相应的计算和简算。学习目标自主学习阅读课本P91-----P92解答下列问题1、P91【问题】 看懂问题,理解列式
2、 P91【思考】 独立思考,不懂的地方用笔标记出来。
3 、熟记法则,要求能理解记忆
4、 P90例2 能利用法则独立完成的将例题做到本上,不能独立完成的自己看书理解,尽最大努力学会,不理解的做好标记时间:6分钟观察、猜想:
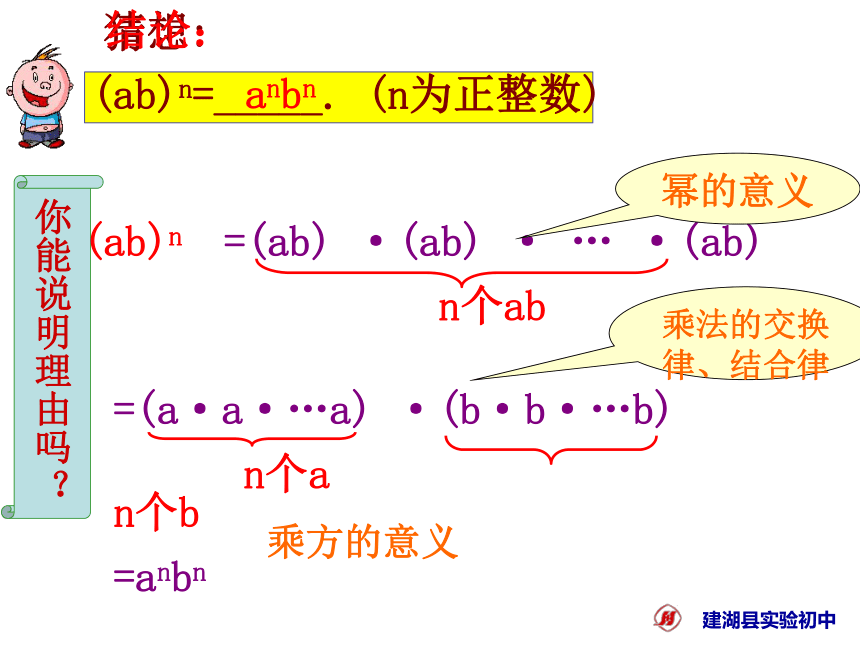
(ab)3与a3b3 是什么关系呢?(ab)3=说出以上推导过程中每一步变形的依据。(ab)·(ab)·(ab)=(aaa) ·(bbb)= a3b3 自学检测:(ab)n=_____.(n为正整数)猜想:你能说明理由吗? =(ab) ·(ab) · … ·(ab)
n个ab
=(a·a·…a) ·(b·b·…b)
n个a n个b
=anbn(ab)n幂的意义乘法的交换律、结合律乘方的意义(ab)n=_____. (n为正整数)anbn结论:积的乘方的运算性质:结论:(ab)n=_____. (n为正整数)anbn你能用文字语言叙述这个性质吗? 积的乘方,把积的每一个因式分别乘方,再把所得的幂相乘.积的乘方的运算性质:(ab)n=_____.(n为正整数)(ab)n=_____. (n为正整数)anbn 积的乘方,把积的每一个因式分别乘方,再把所得的幂相乘.例1 计算:(2m)3 (2) (xy2)3
(3)(-2y3)2 (4) (-5a)3 小试牛刀第一关:每题10分1.计算:
(-ab)5 (2) (x2y3)4
(3) (4×103)2 (4) (-3a3)3××x342.下面的计算是否正确?如果有错误,请改正.
(xy2)3= x y6 ( )
(-2b2)2=-4 b4 ( )1( )
( )
( )
( )
( )1.在括号里填写适当的计算依据:(1)[(3x)2]3
=(3x)6
=36x6
=729x6
(2)[(3x)2]3
=(9x2)3
=93(x2)3
=729x6积的乘方的运算性质积的乘方的运算性质积的乘方的运算性质幂的乘方的运算性质幂的乘方的运算性质乘胜追击第二关:每题20分2.计算:
(1) (-3x2y)3 (2) (-5ab)2
(3) (2xnym)2 (4) (-2xy2z3)4
3.计算:
⑴ (-a2)3.(-a3)2
⑵ -(n2).(-n5)3
⑶ a5.a3+(2a2)4
⑷ (-2a)3-(-a).(a)2=1解:原式你会计算吗?试一试你会计算吗?
×逆用积的乘方的运算性质 一举夺魁第三关:每题30分计算:
解:原式逆用幂的乘方的运算性质幂的乘方的运算性质逆用同底数幂的乘法运算性质逆用积的乘方的运算性质= 一起探讨:(0.04)2004×[(-5)2004]2=?=(0.22)2004 × 54008=(0.2)4008 × 54008=(0.2 ×5)4008=14008解法一: (0.04)2004×[(-5)2004]2=1=(0.04)2004 × [(-5)2]2004=(0.04×25)2004=12004=1= (0.04)2004 ×(25)2004 说明:逆用积的乘方法则 anbn = (ab)n可以解一些复杂的计算。解法二: (0.04)2004×[(-5)2004]2本节课你的收获是什么?小结本节课你学到了什么?{每个因式分别乘方后的积 反向使用
am · an =am+n、
(am)n =amn
an·bn = (ab)n
可使某些计算简捷。小结
2.能利用积的乘方的运算法则进行相应的计算和简算。学习目标自主学习阅读课本P91-----P92解答下列问题1、P91【问题】 看懂问题,理解列式
2、 P91【思考】 独立思考,不懂的地方用笔标记出来。
3 、熟记法则,要求能理解记忆
4、 P90例2 能利用法则独立完成的将例题做到本上,不能独立完成的自己看书理解,尽最大努力学会,不理解的做好标记时间:6分钟观察、猜想:
(ab)3与a3b3 是什么关系呢?(ab)3=说出以上推导过程中每一步变形的依据。(ab)·(ab)·(ab)=(aaa) ·(bbb)= a3b3 自学检测:(ab)n=_____.(n为正整数)猜想:你能说明理由吗? =(ab) ·(ab) · … ·(ab)
n个ab
=(a·a·…a) ·(b·b·…b)
n个a n个b
=anbn(ab)n幂的意义乘法的交换律、结合律乘方的意义(ab)n=_____. (n为正整数)anbn结论:积的乘方的运算性质:结论:(ab)n=_____. (n为正整数)anbn你能用文字语言叙述这个性质吗? 积的乘方,把积的每一个因式分别乘方,再把所得的幂相乘.积的乘方的运算性质:(ab)n=_____.(n为正整数)(ab)n=_____. (n为正整数)anbn 积的乘方,把积的每一个因式分别乘方,再把所得的幂相乘.例1 计算:(2m)3 (2) (xy2)3
(3)(-2y3)2 (4) (-5a)3 小试牛刀第一关:每题10分1.计算:
(-ab)5 (2) (x2y3)4
(3) (4×103)2 (4) (-3a3)3××x342.下面的计算是否正确?如果有错误,请改正.
(xy2)3= x y6 ( )
(-2b2)2=-4 b4 ( )1( )
( )
( )
( )
( )1.在括号里填写适当的计算依据:(1)[(3x)2]3
=(3x)6
=36x6
=729x6
(2)[(3x)2]3
=(9x2)3
=93(x2)3
=729x6积的乘方的运算性质积的乘方的运算性质积的乘方的运算性质幂的乘方的运算性质幂的乘方的运算性质乘胜追击第二关:每题20分2.计算:
(1) (-3x2y)3 (2) (-5ab)2
(3) (2xnym)2 (4) (-2xy2z3)4
3.计算:
⑴ (-a2)3.(-a3)2
⑵ -(n2).(-n5)3
⑶ a5.a3+(2a2)4
⑷ (-2a)3-(-a).(a)2=1解:原式你会计算吗?试一试你会计算吗?
×逆用积的乘方的运算性质 一举夺魁第三关:每题30分计算:
解:原式逆用幂的乘方的运算性质幂的乘方的运算性质逆用同底数幂的乘法运算性质逆用积的乘方的运算性质= 一起探讨:(0.04)2004×[(-5)2004]2=?=(0.22)2004 × 54008=(0.2)4008 × 54008=(0.2 ×5)4008=14008解法一: (0.04)2004×[(-5)2004]2=1=(0.04)2004 × [(-5)2]2004=(0.04×25)2004=12004=1= (0.04)2004 ×(25)2004 说明:逆用积的乘方法则 anbn = (ab)n可以解一些复杂的计算。解法二: (0.04)2004×[(-5)2004]2本节课你的收获是什么?小结本节课你学到了什么?{每个因式分别乘方后的积 反向使用
am · an =am+n、
(am)n =amn
an·bn = (ab)n
可使某些计算简捷。小结
