2021-2022学年人教版数学九年级下册26.2 实际问题与反比例函数 课件(共16张PPT)
文档属性
| 名称 | 2021-2022学年人教版数学九年级下册26.2 实际问题与反比例函数 课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 197.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-21 14:31:52 | ||
图片预览




文档简介
(共16张PPT)
26.2 实际问题与反比例函数
(1)将实际问题抽象成数学问题
(2)利用反比例函数解决实际问题
九年级-下册-第二十六章
26.2 实际问题与反比例函数
(1)将实际问题抽象成数学问题
九年级-下册-第二十六章节
目录
CONTENTS
3
导入
4
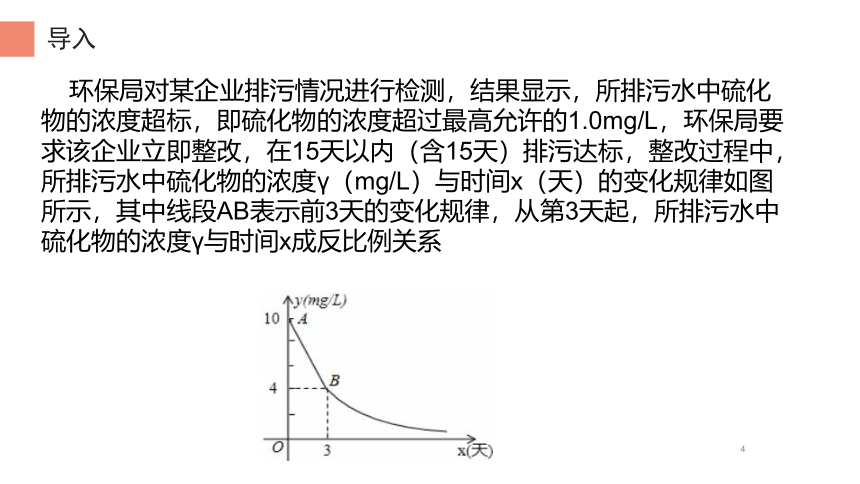
环保局对某企业排污情况进行检测,结果显示,所排污水中硫化物的浓度超标,即硫化物的浓度超过最高允许的1.0mg/L,环保局要求该企业立即整改,在15天以内(含15天)排污达标,整改过程中,所排污水中硫化物的浓度γ(mg/L)与时间x(天)的变化规律如图所示,其中线段AB表示前3天的变化规律,从第3天起,所排污水中硫化物的浓度γ与时间x成反比例关系
导入
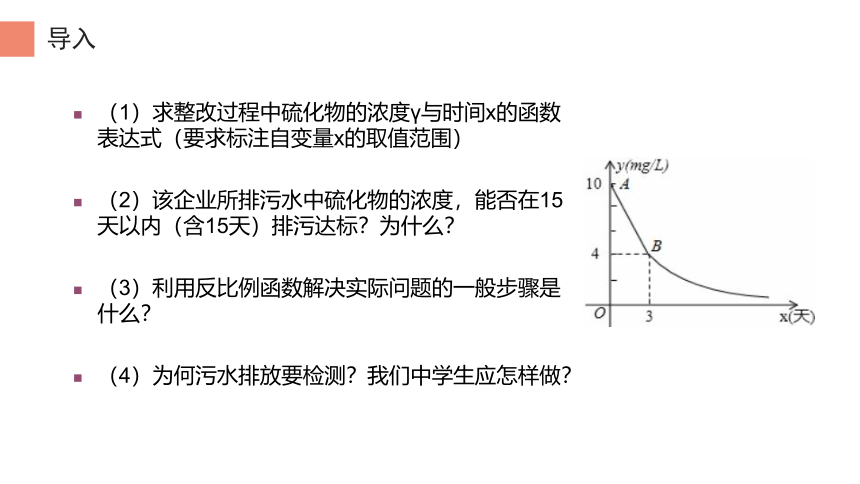
(1)求整改过程中硫化物的浓度γ与时间x的函数表达式(要求标注自变量x的取值范围)
(2)该企业所排污水中硫化物的浓度,能否在15天以内(含15天)排污达标?为什么?
(3)利用反比例函数解决实际问题的一般步骤是什么?
(4)为何污水排放要检测?我们中学生应怎样做?
知识讲解
难点突破
解:(1)分情况讨论:
①当0≤x≤3时,
设线段AB对应的函数表达式为y=kx+b;
把A(0,10),B(3,4)代入并解得:
∴y=﹣2x+10;
②当x>3时,设y=
把(3,4)代入得:m=3×4=12,
∴y= ;
综上所述:当0≤x≤3时,y=﹣2x+10;当x>3时,y= ;
(2)能;理由如下:
令y==1,则x=12,
3<12<15,
故能在15天以内不超过最高允许的1.0mg/L.
课堂练习
7
难点巩固
红星粮库需要把晾晒场上的1200吨玉米入库封存.
(1)入库所需的时间t(单位:天)与入库速度v(单位:吨/天)有怎样的函数关系?
(2)粮库有职工60名,每天最多可入库300吨玉米,预计玉米入库最快可在几日内完成?
(3)粮库的职工连续工作了两天后,天气预报报道在未来的几天很可能会下雨,粮库决定次日把剩下的玉米全部入库,需要增加多少人帮忙才能完成任务?
【课堂小结】
小结
应用反比例函数解决实际问题的一般步骤:
一.搞清题目中的基本数量关系,建立数学模型,将实际问题抽象成数学问题;
二.分清自变量与函数,以便写出正确的函数关系式,并注意自变量的取值范围;
三.熟练掌握反比例函数的意义图象和性质,要数形结合,这样有利于解决问题。
26.2 实际问题与反比例函数
(2)利用反比例函数解决实际问题
九年级-下册-第二十六章
目录
CONTENTS
导入
《城镇污水处理厂污染物排放标准》中硫化物的排放标准为1.0mg/L.某污水处理厂在自查中发现,所排污水中硫化物浓度超标,因此立即整改,并开始实时数据监测。整改开始第60小时时,所排污水中硫化物的浓度为5mg/L;从第60小时开始,所排污水中硫化物的浓度y(mg/L)是监测时间x(小时)的反比例函数其图象如图所示。
反比例函数实际问题
(1)求y与x的函数关系式;
(1)设y与x的函数关系式为y= (x>0),
∵将(60,5)代入;
∴5= ,
解得:k=300,
∴y与x的函数关系式为y= .
(2)当x=100时,y= =3,
(3)当y=0.8时,0.8= ,
解得x=375,
答:此次整改实时监测的时间至少为375小时.
(2)整改开始第100小时时,所排污水中硫化物浓度为_____mg/L;
(3)按规定所排污水中硫化物的浓度不超过0.8mg/L时,才能解除实时监测,此次整改实时监测的时间至少为多少小时?
知识讲解
难点突破
为了预防流感,某学校在星期天用药熏消毒法对教室进行消毒.已知药物释放过程中,室内每立方米空气中的含药量 y(毫克)与时间 t(小时)成正比;药物释放完毕后,y 与 t 的函数关系式为 (a为常数).如图所示,据图中提供的信息,解答下列问题:
难点巩固
课堂练习
(1)写出从药物释放开始,y 与 t 之间的两个函数关系式及相应的自变量的取值范围;
解:(1)药物释放过程:
药物释放完毕后:
(2)据测定,当空气中每立方米的含药量降低到 0.25 毫克以下时,学生方可进入教室,那么从药物释放开始,至少需要经过多少小时后,学生才能进入教室?
解:(2)当 y = 0.25 毫克时,由 得
(小时),至少需要经过 6 小时后,学生才能进入教室.
谢谢聆听
26.2 实际问题与反比例函数
(1)将实际问题抽象成数学问题
(2)利用反比例函数解决实际问题
九年级-下册-第二十六章
26.2 实际问题与反比例函数
(1)将实际问题抽象成数学问题
九年级-下册-第二十六章节
目录
CONTENTS
3
导入
4
环保局对某企业排污情况进行检测,结果显示,所排污水中硫化物的浓度超标,即硫化物的浓度超过最高允许的1.0mg/L,环保局要求该企业立即整改,在15天以内(含15天)排污达标,整改过程中,所排污水中硫化物的浓度γ(mg/L)与时间x(天)的变化规律如图所示,其中线段AB表示前3天的变化规律,从第3天起,所排污水中硫化物的浓度γ与时间x成反比例关系
导入
(1)求整改过程中硫化物的浓度γ与时间x的函数表达式(要求标注自变量x的取值范围)
(2)该企业所排污水中硫化物的浓度,能否在15天以内(含15天)排污达标?为什么?
(3)利用反比例函数解决实际问题的一般步骤是什么?
(4)为何污水排放要检测?我们中学生应怎样做?
知识讲解
难点突破
解:(1)分情况讨论:
①当0≤x≤3时,
设线段AB对应的函数表达式为y=kx+b;
把A(0,10),B(3,4)代入并解得:
∴y=﹣2x+10;
②当x>3时,设y=
把(3,4)代入得:m=3×4=12,
∴y= ;
综上所述:当0≤x≤3时,y=﹣2x+10;当x>3时,y= ;
(2)能;理由如下:
令y==1,则x=12,
3<12<15,
故能在15天以内不超过最高允许的1.0mg/L.
课堂练习
7
难点巩固
红星粮库需要把晾晒场上的1200吨玉米入库封存.
(1)入库所需的时间t(单位:天)与入库速度v(单位:吨/天)有怎样的函数关系?
(2)粮库有职工60名,每天最多可入库300吨玉米,预计玉米入库最快可在几日内完成?
(3)粮库的职工连续工作了两天后,天气预报报道在未来的几天很可能会下雨,粮库决定次日把剩下的玉米全部入库,需要增加多少人帮忙才能完成任务?
【课堂小结】
小结
应用反比例函数解决实际问题的一般步骤:
一.搞清题目中的基本数量关系,建立数学模型,将实际问题抽象成数学问题;
二.分清自变量与函数,以便写出正确的函数关系式,并注意自变量的取值范围;
三.熟练掌握反比例函数的意义图象和性质,要数形结合,这样有利于解决问题。
26.2 实际问题与反比例函数
(2)利用反比例函数解决实际问题
九年级-下册-第二十六章
目录
CONTENTS
导入
《城镇污水处理厂污染物排放标准》中硫化物的排放标准为1.0mg/L.某污水处理厂在自查中发现,所排污水中硫化物浓度超标,因此立即整改,并开始实时数据监测。整改开始第60小时时,所排污水中硫化物的浓度为5mg/L;从第60小时开始,所排污水中硫化物的浓度y(mg/L)是监测时间x(小时)的反比例函数其图象如图所示。
反比例函数实际问题
(1)求y与x的函数关系式;
(1)设y与x的函数关系式为y= (x>0),
∵将(60,5)代入;
∴5= ,
解得:k=300,
∴y与x的函数关系式为y= .
(2)当x=100时,y= =3,
(3)当y=0.8时,0.8= ,
解得x=375,
答:此次整改实时监测的时间至少为375小时.
(2)整改开始第100小时时,所排污水中硫化物浓度为_____mg/L;
(3)按规定所排污水中硫化物的浓度不超过0.8mg/L时,才能解除实时监测,此次整改实时监测的时间至少为多少小时?
知识讲解
难点突破
为了预防流感,某学校在星期天用药熏消毒法对教室进行消毒.已知药物释放过程中,室内每立方米空气中的含药量 y(毫克)与时间 t(小时)成正比;药物释放完毕后,y 与 t 的函数关系式为 (a为常数).如图所示,据图中提供的信息,解答下列问题:
难点巩固
课堂练习
(1)写出从药物释放开始,y 与 t 之间的两个函数关系式及相应的自变量的取值范围;
解:(1)药物释放过程:
药物释放完毕后:
(2)据测定,当空气中每立方米的含药量降低到 0.25 毫克以下时,学生方可进入教室,那么从药物释放开始,至少需要经过多少小时后,学生才能进入教室?
解:(2)当 y = 0.25 毫克时,由 得
(小时),至少需要经过 6 小时后,学生才能进入教室.
谢谢聆听
