2021-2022学年人教版数学九年级下册28.2 解直角三角形及其应用 课件(共20张PPT)
文档属性
| 名称 | 2021-2022学年人教版数学九年级下册28.2 解直角三角形及其应用 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 681.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-21 14:36:14 | ||
图片预览








文档简介
(共20张PPT)
28.2 解直角三角形及其应用
(1)解直角三角形
(2)将实际问题抽象成数学问题
人教版数学九级下册
解直角三角形
(1)三边之间的关系
a2+b2=c2(勾股定理) ;
(2)两锐角之间的关系
∠A+∠B=90°;
(3)边角之间的关系
在直角三角形中,除直角外的五个元素之间有哪些关系?
知道五个元素中的两个,就可以求其余元素。
(注意:至少有一个元素是边).
已知两边:可以求出第三边和两个锐角.
已知一边和一锐角:可以求出另一个锐角和另两条边.
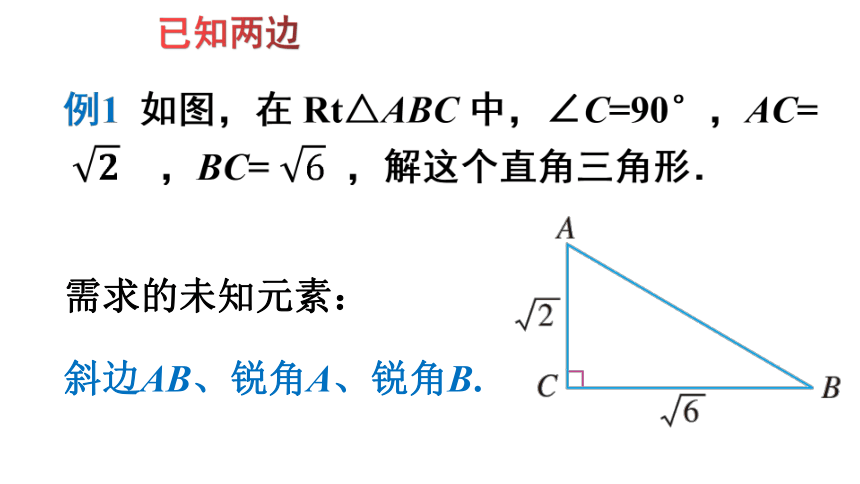
需求的未知元素:
斜边AB、锐角A、锐角B.
已知两边
方法一:
方法二:
例2 如图,在 Rt△ABC中,∠C=90°,∠B=
35°,b=20,解这个直角三角形(参考数据:sin35°≈0.5736,cos35°≈0.8192,tan35°≈0.7002,结果保留小数点后一位).
需求的未知元素:
直角边a、斜边c、锐角A.
已知一边和一锐角
b
解:∠A=90°-∠B=90°-35°=55° ,
b=20
1.已知在Rt△ABC中,∠C=90°.
(1)若a= ,b= ,则c= ;
(2)若a=10,c= ,则∠B= ;
(3)若b=35,∠A=45°,则a= ;
(4)若c=20,∠A=60°,则a= .
课堂练习
45°
35
2.如图,在Rt△ABC中,∠BAC=90°,点D在BC边上,且△ABD是等边三角形.若AB=2,求△ABC的周长.(结果保留根号)
解:∵△ABD是等边三角形,∴∠B=60°.
在Rt△ABC中,AB=2,∠B=60°,
△ABC的周长为2+ +4=6+
课堂小结
解直角三角形
在直角三角形中,由已知元素求出未知元素的过程,叫做解直角三角形.
两边:两直角边或斜边、一直角边
一边一角:直角边、一锐角或斜边、一锐角
将实际问题抽象成数学问题
导入
13
例: 热气球的探测器显示,从热气球看一栋楼顶部的仰角为30°,看这栋楼底部的俯角是60°,热气球与
楼的水平距离是120米,这栋楼有多高?(结果保留根号)
分析:我们知道,在视线与水平线所成的角中,视线在水平线上方的是
仰角,视线在水平线下方的是俯角。因此,这道题需要过点A做AD的垂线
交BC于点D,构造出两个直角三角形,AD=120,∠BAD=30°,∠DAC=60°,
利用解直角三角形的知识求出BD,类似的求出CD,进而求得BC.
活动与探究(温馨提示:规范操作、注意安全)
知识讲解
难点突破
解:如图,过点A作 AD⊥BC ,垂足为D,则∠BAD=30°,∠DAC=60°,AD=120
在Rt△ABD中,tan∠BAD=tan30°= ,tan∠BAD=tan60°=
∴BD=AD tan30°=120× =40
∴CD=AD tan60°=120× =120
∴BC=BD+CD=160
答:楼的高度为160 米
思路点拨:在三角形内部作高构造直角三角形,在两个直角三角形中
利用锐角三角函数求边长,进而获得实际问题的答案。
课堂练习
15
难点巩固
变式一(2016年自治区兵团19题8分):
在地面C处测得楼顶A的仰角为30度,前进16米到D处测得楼顶的仰角为45度,求楼高AB(结果保留整数)
解:设AB=X,因为∠ADB=45°,所以∠DAB=45°,所以DB=AB=X
∴BC=16+X
在Rt△ABC中,∠B=90°,tan30°= = =
∴X=8 +8≈22
经检验,X=8 +8是原方程的解且符合题意
答:楼AB的高度约为22米
思路点拨:在一个直角三角形中设未知数创造条件,在另一个直角三角形中建立等量关系解方程
课堂练习
变式二:
在离地面高2米的A处测顶B的仰角为30°,由F前进8到达D处,测到B的仰角为60°,求楼
BE的高度(结果保留根号)
解:由题意可知,∠1=30°,∠2=60°,AD=2,DF=8,设DE=X
∵在Rt△BDE中,BD=2X,由勾股定理得BE= X
∵∠D=∠C=∠AEC=90° ∴四边形ADCE是矩形
∴AF=EC=2,AC=EF=8+X
在Rt△ABC中,tan∠BAC=tan30°= = =
∴X=4+ 经检验,X=4+ 是原方程的解且符合题意
答:楼高(4 +3)米。
【课堂小结】
小结
根据实际需要新增页
基本模型总结:背靠背型
方法总结:在三角形内部作高构造直角三角形,利用锐角三角函数解决问题
基本模型总结:母子型
方法总结:构造直角三角形,在一个直角三角形中设未知数创造条件,在另一直角三角形中建立等量关系
解方程,求数学问题的解,进而获得实际问题的解,若含有矩形,要利用矩形的性质找相等的量。
1.从课后习题中选取;
2.完成同步练习册本课时的习题。
布置作业
感 谢 聆 听
28.2 解直角三角形及其应用
(1)解直角三角形
(2)将实际问题抽象成数学问题
人教版数学九级下册
解直角三角形
(1)三边之间的关系
a2+b2=c2(勾股定理) ;
(2)两锐角之间的关系
∠A+∠B=90°;
(3)边角之间的关系
在直角三角形中,除直角外的五个元素之间有哪些关系?
知道五个元素中的两个,就可以求其余元素。
(注意:至少有一个元素是边).
已知两边:可以求出第三边和两个锐角.
已知一边和一锐角:可以求出另一个锐角和另两条边.
需求的未知元素:
斜边AB、锐角A、锐角B.
已知两边
方法一:
方法二:
例2 如图,在 Rt△ABC中,∠C=90°,∠B=
35°,b=20,解这个直角三角形(参考数据:sin35°≈0.5736,cos35°≈0.8192,tan35°≈0.7002,结果保留小数点后一位).
需求的未知元素:
直角边a、斜边c、锐角A.
已知一边和一锐角
b
解:∠A=90°-∠B=90°-35°=55° ,
b=20
1.已知在Rt△ABC中,∠C=90°.
(1)若a= ,b= ,则c= ;
(2)若a=10,c= ,则∠B= ;
(3)若b=35,∠A=45°,则a= ;
(4)若c=20,∠A=60°,则a= .
课堂练习
45°
35
2.如图,在Rt△ABC中,∠BAC=90°,点D在BC边上,且△ABD是等边三角形.若AB=2,求△ABC的周长.(结果保留根号)
解:∵△ABD是等边三角形,∴∠B=60°.
在Rt△ABC中,AB=2,∠B=60°,
△ABC的周长为2+ +4=6+
课堂小结
解直角三角形
在直角三角形中,由已知元素求出未知元素的过程,叫做解直角三角形.
两边:两直角边或斜边、一直角边
一边一角:直角边、一锐角或斜边、一锐角
将实际问题抽象成数学问题
导入
13
例: 热气球的探测器显示,从热气球看一栋楼顶部的仰角为30°,看这栋楼底部的俯角是60°,热气球与
楼的水平距离是120米,这栋楼有多高?(结果保留根号)
分析:我们知道,在视线与水平线所成的角中,视线在水平线上方的是
仰角,视线在水平线下方的是俯角。因此,这道题需要过点A做AD的垂线
交BC于点D,构造出两个直角三角形,AD=120,∠BAD=30°,∠DAC=60°,
利用解直角三角形的知识求出BD,类似的求出CD,进而求得BC.
活动与探究(温馨提示:规范操作、注意安全)
知识讲解
难点突破
解:如图,过点A作 AD⊥BC ,垂足为D,则∠BAD=30°,∠DAC=60°,AD=120
在Rt△ABD中,tan∠BAD=tan30°= ,tan∠BAD=tan60°=
∴BD=AD tan30°=120× =40
∴CD=AD tan60°=120× =120
∴BC=BD+CD=160
答:楼的高度为160 米
思路点拨:在三角形内部作高构造直角三角形,在两个直角三角形中
利用锐角三角函数求边长,进而获得实际问题的答案。
课堂练习
15
难点巩固
变式一(2016年自治区兵团19题8分):
在地面C处测得楼顶A的仰角为30度,前进16米到D处测得楼顶的仰角为45度,求楼高AB(结果保留整数)
解:设AB=X,因为∠ADB=45°,所以∠DAB=45°,所以DB=AB=X
∴BC=16+X
在Rt△ABC中,∠B=90°,tan30°= = =
∴X=8 +8≈22
经检验,X=8 +8是原方程的解且符合题意
答:楼AB的高度约为22米
思路点拨:在一个直角三角形中设未知数创造条件,在另一个直角三角形中建立等量关系解方程
课堂练习
变式二:
在离地面高2米的A处测顶B的仰角为30°,由F前进8到达D处,测到B的仰角为60°,求楼
BE的高度(结果保留根号)
解:由题意可知,∠1=30°,∠2=60°,AD=2,DF=8,设DE=X
∵在Rt△BDE中,BD=2X,由勾股定理得BE= X
∵∠D=∠C=∠AEC=90° ∴四边形ADCE是矩形
∴AF=EC=2,AC=EF=8+X
在Rt△ABC中,tan∠BAC=tan30°= = =
∴X=4+ 经检验,X=4+ 是原方程的解且符合题意
答:楼高(4 +3)米。
【课堂小结】
小结
根据实际需要新增页
基本模型总结:背靠背型
方法总结:在三角形内部作高构造直角三角形,利用锐角三角函数解决问题
基本模型总结:母子型
方法总结:构造直角三角形,在一个直角三角形中设未知数创造条件,在另一直角三角形中建立等量关系
解方程,求数学问题的解,进而获得实际问题的解,若含有矩形,要利用矩形的性质找相等的量。
1.从课后习题中选取;
2.完成同步练习册本课时的习题。
布置作业
感 谢 聆 听
