2021-2022学年人教版数学九年级下册28.2.2 应用举例 课件(共20张PPT)
文档属性
| 名称 | 2021-2022学年人教版数学九年级下册28.2.2 应用举例 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 760.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-21 00:00:00 | ||
图片预览






文档简介
(共20张PPT)
28.2.2 应用举例
(1)解与方位角有关的实际问题
(2)解直三角形的应用
人教版数学九级下册
28.2 解直角三角形及其应用
解与方位角有关的实际问题
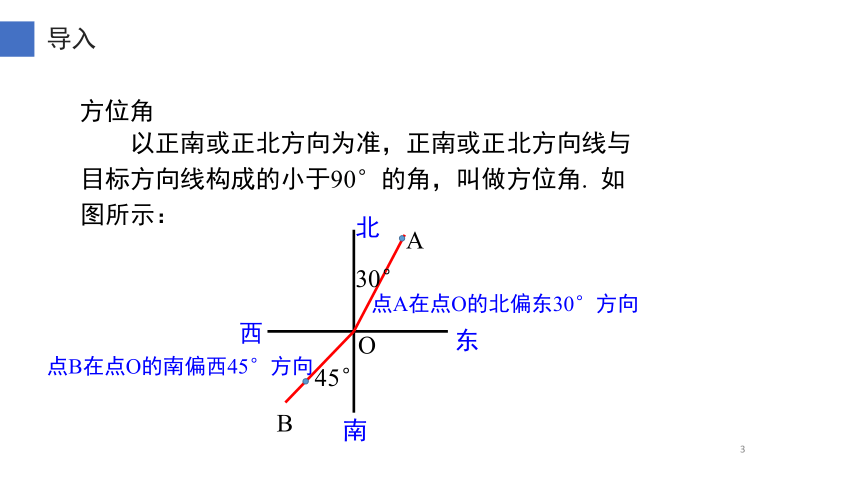
导入
3
以正南或正北方向为准,正南或正北方向线与目标方向线构成的小于90°的角,叫做方位角. 如图所示:
方位角
点A在点O的北偏东30°方向
点B在点O的南偏西45°方向
30°
45°
B
O
A
东
西
北
南
活动与探究(温馨提示:规范操作、注意安全)
知识讲解
难点突破
解与方位角有关的问题
例1、 如图,一艘海轮位于灯塔P的北偏东60°方向,距离灯塔80n mine的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东30°方向上的B处,这时,海轮所在的B处距离灯塔P有多远(结果取整数)?
60°
30°
P
B
C
A
例题讲解
80
30°
30°
E
F
解:由题意得∠FPA=60°∠EPB=30°AB⊥PC EF∥AB
因此,当海轮到达位于灯塔P的南偏东30°方向时,它距离灯塔P大约139n mine.
∴∠B=∠EPB=30°,∠APC=90°-∠FPA=90°-60°=30°
5
归
纳
利用解直角三角形的知识解决实际问题的一般过程是:
(1)将实际问题抽象为数学问题(画出平面图形,转化为解直角三角形的问题);
(2)根据条件的特点,适当选用锐角三角形函数等去解直角三角形;
(3)得到数学问题的答案;
(4)得到实际问题的答案.
知识讲解
难点突破
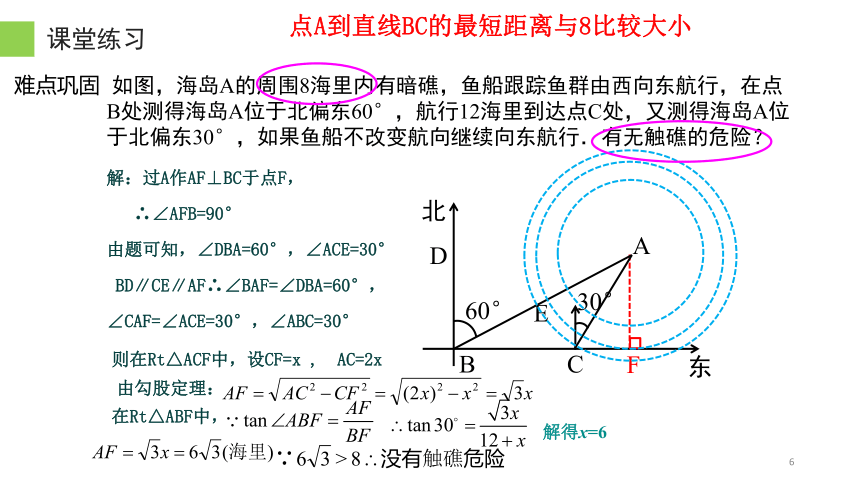
课堂练习
6
难点巩固
解:过A作AF⊥BC于点F,
∴∠AFB=90°
由题可知,∠DBA=60°,∠ACE=30°
BD∥CE∥AF∴∠BAF=∠DBA=60°,
∠CAF=∠ACE=30°,∠ABC=30°
如图,海岛A的周围8海里内有暗礁,鱼船跟踪鱼群由西向东航行,在点B处测得海岛A位于北偏东60°,航行12海里到达点C处,又测得海岛A位于北偏东30°,如果鱼船不改变航向继续向东航行.有无触礁的危险?
北
东
A
C
B
60°
30°
D
E
F
点A到直线BC的最短距离与8比较大小
解得x=6
则在Rt△ACF中,设CF=x , AC=2x
由勾股定理:
在Rt△ABF中,
【课堂小结】
小结
1、要弄清方位角的概念,明确各术语与示意图中的什么元素对应,只有明确这些概念,才能恰当地把实际问题转化为数学问题 。
2、认真分析题意、画图并找出要求的直角三角形,或通过添加辅助线构造直角三角形来解决问题。
3、选择合适的边角关系式,使计算尽可能简单,且不易出错。
4、按照题中的精确度进行计算,并按照题目中要求的精确度确定答案以及注明单位。
解直三角形的应用
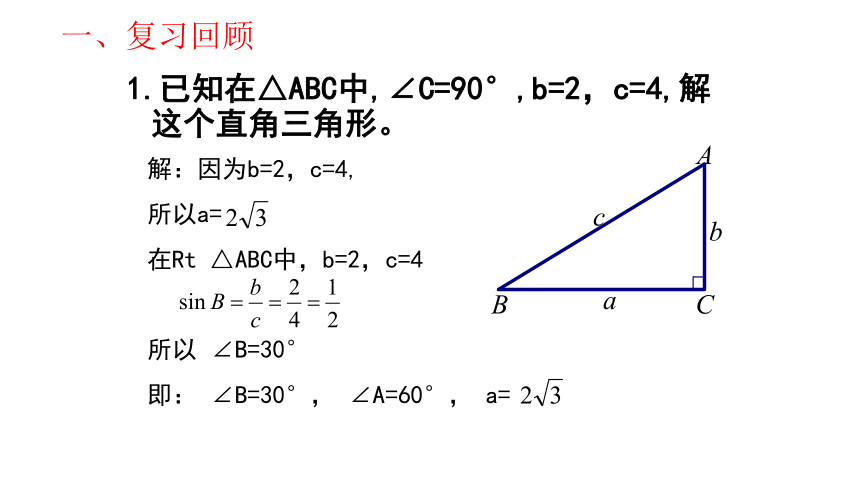
一、复习回顾
1.已知在△ABC中,∠C=90°,b=2,c=4,解这个直角三角形。
解:因为b=2,c=4,
所以a=
在Rt △ABC中,b=2,c=4
所以 ∠B=30°
即: ∠B=30°, ∠A=60°, a=
学习目标
1、把实际问题转化为解直角三角形问题。
2、综合运用直角三角形相关知识解直角三角形。
3、进一步了解数学建模思想,数形结合的数学思想。
知识储备:仰角、俯角
视线
仰角
俯角
铅垂线
水平线
视线在水平线上方的角叫做仰角
视线在水平线下方的角叫做俯角
视线
如图, BCA= DEB=90 ,FB//AC // DE,
从A看B的仰角是______;
从B看A的俯角是 。
从B看D的俯角是 ;
从D看B的仰角是 ;
D
A
C
E
B
F
∠FBD
∠BDE
∠FBA
试一试
∠BAC
水平线
【探究1】热气球的探测器显示,从热气球看一栋高楼顶部B点的仰角为30°,看这栋高楼底部C点的俯角为60°,热气球与高楼的水平距离为120m,这栋高楼有多高(结果保留根号)
二、探究新知
建筑物BC上有一旗杆AB,由距BC 40m的D处观察旗杆顶部A的仰角54°,观察底部B 的仰角为45°,求旗杆的高度(精确到0.1m)
参考数据:
A
B
C
D
40m
54°
45°
A
B
C
D
40m
54°
45°
小试牛刀
【探究2】直升飞机在跨江大桥AB的上方P点处,此时飞机离地面的高度450米,且A、B、O三点在一条直线上,测得大桥两端的俯角分别为30°和45°求大桥的宽AB(结果保留根号)。
如图,为测量建筑物的高度,在点A测得建筑物顶部D点的仰角为22°,再向建筑物前进30米到达点B,测得建筑物顶部D点的仰角为58°,A、B、C三点在一条直线上,求建筑物的高度(结果保留整数)
参考数据:
三、课堂练习
四、课堂小结:
1、解决实际问题方法:解直角三角形的知识
2、解决实际问题的流程:
实际问题
数学问题
实际问题的解
解数学问题
抽 象
转化思想
五、布置作业:
A层:课本第84页练习7、8、9题。
B层:课本第76页练习1、2题。
用数学视角观察世界
用数学思维思考世界
感 谢 聆 听
28.2.2 应用举例
(1)解与方位角有关的实际问题
(2)解直三角形的应用
人教版数学九级下册
28.2 解直角三角形及其应用
解与方位角有关的实际问题
导入
3
以正南或正北方向为准,正南或正北方向线与目标方向线构成的小于90°的角,叫做方位角. 如图所示:
方位角
点A在点O的北偏东30°方向
点B在点O的南偏西45°方向
30°
45°
B
O
A
东
西
北
南
活动与探究(温馨提示:规范操作、注意安全)
知识讲解
难点突破
解与方位角有关的问题
例1、 如图,一艘海轮位于灯塔P的北偏东60°方向,距离灯塔80n mine的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东30°方向上的B处,这时,海轮所在的B处距离灯塔P有多远(结果取整数)?
60°
30°
P
B
C
A
例题讲解
80
30°
30°
E
F
解:由题意得∠FPA=60°∠EPB=30°AB⊥PC EF∥AB
因此,当海轮到达位于灯塔P的南偏东30°方向时,它距离灯塔P大约139n mine.
∴∠B=∠EPB=30°,∠APC=90°-∠FPA=90°-60°=30°
5
归
纳
利用解直角三角形的知识解决实际问题的一般过程是:
(1)将实际问题抽象为数学问题(画出平面图形,转化为解直角三角形的问题);
(2)根据条件的特点,适当选用锐角三角形函数等去解直角三角形;
(3)得到数学问题的答案;
(4)得到实际问题的答案.
知识讲解
难点突破
课堂练习
6
难点巩固
解:过A作AF⊥BC于点F,
∴∠AFB=90°
由题可知,∠DBA=60°,∠ACE=30°
BD∥CE∥AF∴∠BAF=∠DBA=60°,
∠CAF=∠ACE=30°,∠ABC=30°
如图,海岛A的周围8海里内有暗礁,鱼船跟踪鱼群由西向东航行,在点B处测得海岛A位于北偏东60°,航行12海里到达点C处,又测得海岛A位于北偏东30°,如果鱼船不改变航向继续向东航行.有无触礁的危险?
北
东
A
C
B
60°
30°
D
E
F
点A到直线BC的最短距离与8比较大小
解得x=6
则在Rt△ACF中,设CF=x , AC=2x
由勾股定理:
在Rt△ABF中,
【课堂小结】
小结
1、要弄清方位角的概念,明确各术语与示意图中的什么元素对应,只有明确这些概念,才能恰当地把实际问题转化为数学问题 。
2、认真分析题意、画图并找出要求的直角三角形,或通过添加辅助线构造直角三角形来解决问题。
3、选择合适的边角关系式,使计算尽可能简单,且不易出错。
4、按照题中的精确度进行计算,并按照题目中要求的精确度确定答案以及注明单位。
解直三角形的应用
一、复习回顾
1.已知在△ABC中,∠C=90°,b=2,c=4,解这个直角三角形。
解:因为b=2,c=4,
所以a=
在Rt △ABC中,b=2,c=4
所以 ∠B=30°
即: ∠B=30°, ∠A=60°, a=
学习目标
1、把实际问题转化为解直角三角形问题。
2、综合运用直角三角形相关知识解直角三角形。
3、进一步了解数学建模思想,数形结合的数学思想。
知识储备:仰角、俯角
视线
仰角
俯角
铅垂线
水平线
视线在水平线上方的角叫做仰角
视线在水平线下方的角叫做俯角
视线
如图, BCA= DEB=90 ,FB//AC // DE,
从A看B的仰角是______;
从B看A的俯角是 。
从B看D的俯角是 ;
从D看B的仰角是 ;
D
A
C
E
B
F
∠FBD
∠BDE
∠FBA
试一试
∠BAC
水平线
【探究1】热气球的探测器显示,从热气球看一栋高楼顶部B点的仰角为30°,看这栋高楼底部C点的俯角为60°,热气球与高楼的水平距离为120m,这栋高楼有多高(结果保留根号)
二、探究新知
建筑物BC上有一旗杆AB,由距BC 40m的D处观察旗杆顶部A的仰角54°,观察底部B 的仰角为45°,求旗杆的高度(精确到0.1m)
参考数据:
A
B
C
D
40m
54°
45°
A
B
C
D
40m
54°
45°
小试牛刀
【探究2】直升飞机在跨江大桥AB的上方P点处,此时飞机离地面的高度450米,且A、B、O三点在一条直线上,测得大桥两端的俯角分别为30°和45°求大桥的宽AB(结果保留根号)。
如图,为测量建筑物的高度,在点A测得建筑物顶部D点的仰角为22°,再向建筑物前进30米到达点B,测得建筑物顶部D点的仰角为58°,A、B、C三点在一条直线上,求建筑物的高度(结果保留整数)
参考数据:
三、课堂练习
四、课堂小结:
1、解决实际问题方法:解直角三角形的知识
2、解决实际问题的流程:
实际问题
数学问题
实际问题的解
解数学问题
抽 象
转化思想
五、布置作业:
A层:课本第84页练习7、8、9题。
B层:课本第76页练习1、2题。
用数学视角观察世界
用数学思维思考世界
感 谢 聆 听
