18.1.2 平行四边形的性质(2) 课件(共19张PPT)
文档属性
| 名称 | 18.1.2 平行四边形的性质(2) 课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-22 13:38:17 | ||
图片预览





文档简介
(共19张PPT)
2022年春华师大版数学
八年级下册数学精品课件
18.1.2 平行四边形的性质(2)
学习目标
熟练运用平行四边形的性质1、2解决具体问题.
加深对平行四边形的性质1、2的深入理解.
两组对边分别平行的四边形叫做平行四边形.
读作:平行四边形ABCD
A
D
B
C
记作: ABCD
AB∥CD
AD∥BC
∵
∴四边形ABCD是平行四边形
∵四边形ABCD是平行四边形
AB∥CD
AD∥BC
∴
几何语言:
复习回顾
几何语言:
平行四边形定理1:平行四边形的两组对边分别相等.
在 ABCD中,
AB=CD,AD=BC.(平行四边形的对边相等)
∠A=∠C, ∠B=∠D
(平行四边形的对角相等)
∠A+∠B=180° ∠A+∠D =180°
(平行四边的邻角互补)
平行四边形定理2:平行四边形的两组对角分别相等.
推论: 平行四边的邻角互补.
复习回顾
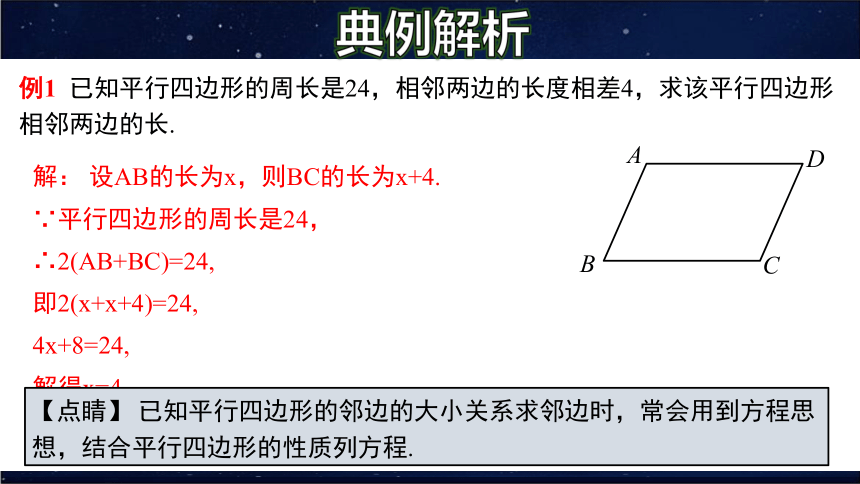
例1 已知平行四边形的周长是24,相邻两边的长度相差4,求该平行四边形相邻两边的长.
解: 设AB的长为x,则BC的长为x+4.
∵平行四边形的周长是24,
∴2(AB+BC)=24,
即2(x+x+4)=24,
4x+8=24,
解得x=4
∴平行四边形相邻两边的长分别为4和8.
D
A
B
C
典例解析
【点睛】 已知平行四边形的邻边的大小关系求邻边时,常会用到方程思想,结合平行四边形的性质列方程.
若 ABCD的周长为28cm,AB:BC=3:4,求各边的长度.
解: 在平行四边形ABCD中,
∵AB=CD,BC=AD.
又∵AB+BC+CD+AD=28cm,
∴AB+BC= 14cm.
∵AB:BC=3:4,设AB=3ycm,BC=4ycm,
∴3y+4y=14,解得y=2.
∴AB=CD=6cm,BC=AD=8cm.
针对练习
典例解析
例2 已知在平行四边形ABCD中,∠ADC的平分线与AB相较于点E.
求证:BE+BC=CD.
解: ∵四边形ABCD是平行四边形,
∴AB=CD(平行四边形的对边相等),
AB∥CD(平行四边形的对边平行),
∴∠CDE=∠AED.
又∵DE是∠ADE的平分线,
∴∠ADE=∠CDE,
∴∠ADE=∠AED,
∴AD=AE.
又∵AD=BC
∴AE=BC.
∴BE+BC=BE+AE=CD.
证明:∵四边形ABCD是平行四边形,
如图,在 ABCD中,E,F是对角线AC上的两点,并且AE=CF,求证: BE=DF.
∴∠BAE=∠DCF.
∴ △ABE≌ △CDF.
∴ AB=CD,AB ∥ CD
又∵AE=CF,
∴BE=DF.
A
D
B
C
E
F
针对练习
1.如图,在平行四边形ABCD中,若AE平分∠DAB,AB=5cm,AD=9cm,则EC= .
C
4cm
A
B
D
E
达标检测
2.如图,在 ABCD中,DE⊥AB,BF⊥CD,垂足分别是E,F.求证:AE=CF.
证明: ∵四边形ABCD是平行四边形,
∴ ∠A= ∠C,AD=CB.
又∠AED= ∠CFB=90°,
∴ △ADE≌△CBF(AAS),
∴AE=CF.
D
A
B
C
F
E
达标检测
3.在 ABCD中,E、F是AC上的两点,AE=CF,求证:BE=DF.
A
B
C
D
E
F
∴∠BAE=∠DCF
∵在△ABE 和△CDF中,AB=CD,
∠BAE=∠DCF, AE=CF
∴△ABE≌△CDF(SAS), BE=DF
证明: ∵在 ABCD中,AB//CD
达标检测
4.如图,在 ABCD中,E,F是直线BD上的两点,且DE=BF,求证:AE=CF.
证明: ∵四边形ABCD 是平行四边形
∴ ∠ADB= ∠CBD , AD=CB
∵ E,F是直线BD上的两点
∴ ∠ADE=180 -∠ADB,∠CBF=180 -∠CBD, ∴∠ADE= ∠CBF
A
E
B
C
F
D
∵ 在△ADE和△CBF中,DE=BF,∠ADE=∠CBF,AD=CB.
∴△ADE≌△CBF (SAS), AE=CF.
达标检测
达标检测
5.
达标检测
6.
达标检测
7.
达标检测
https://www.21cnjy.com/help/help_extract.php
2022年春华师大版数学
八年级下册数学精品课件
18.1.2 平行四边形的性质(2)
学习目标
熟练运用平行四边形的性质1、2解决具体问题.
加深对平行四边形的性质1、2的深入理解.
两组对边分别平行的四边形叫做平行四边形.
读作:平行四边形ABCD
A
D
B
C
记作: ABCD
AB∥CD
AD∥BC
∵
∴四边形ABCD是平行四边形
∵四边形ABCD是平行四边形
AB∥CD
AD∥BC
∴
几何语言:
复习回顾
几何语言:
平行四边形定理1:平行四边形的两组对边分别相等.
在 ABCD中,
AB=CD,AD=BC.(平行四边形的对边相等)
∠A=∠C, ∠B=∠D
(平行四边形的对角相等)
∠A+∠B=180° ∠A+∠D =180°
(平行四边的邻角互补)
平行四边形定理2:平行四边形的两组对角分别相等.
推论: 平行四边的邻角互补.
复习回顾
例1 已知平行四边形的周长是24,相邻两边的长度相差4,求该平行四边形相邻两边的长.
解: 设AB的长为x,则BC的长为x+4.
∵平行四边形的周长是24,
∴2(AB+BC)=24,
即2(x+x+4)=24,
4x+8=24,
解得x=4
∴平行四边形相邻两边的长分别为4和8.
D
A
B
C
典例解析
【点睛】 已知平行四边形的邻边的大小关系求邻边时,常会用到方程思想,结合平行四边形的性质列方程.
若 ABCD的周长为28cm,AB:BC=3:4,求各边的长度.
解: 在平行四边形ABCD中,
∵AB=CD,BC=AD.
又∵AB+BC+CD+AD=28cm,
∴AB+BC= 14cm.
∵AB:BC=3:4,设AB=3ycm,BC=4ycm,
∴3y+4y=14,解得y=2.
∴AB=CD=6cm,BC=AD=8cm.
针对练习
典例解析
例2 已知在平行四边形ABCD中,∠ADC的平分线与AB相较于点E.
求证:BE+BC=CD.
解: ∵四边形ABCD是平行四边形,
∴AB=CD(平行四边形的对边相等),
AB∥CD(平行四边形的对边平行),
∴∠CDE=∠AED.
又∵DE是∠ADE的平分线,
∴∠ADE=∠CDE,
∴∠ADE=∠AED,
∴AD=AE.
又∵AD=BC
∴AE=BC.
∴BE+BC=BE+AE=CD.
证明:∵四边形ABCD是平行四边形,
如图,在 ABCD中,E,F是对角线AC上的两点,并且AE=CF,求证: BE=DF.
∴∠BAE=∠DCF.
∴ △ABE≌ △CDF.
∴ AB=CD,AB ∥ CD
又∵AE=CF,
∴BE=DF.
A
D
B
C
E
F
针对练习
1.如图,在平行四边形ABCD中,若AE平分∠DAB,AB=5cm,AD=9cm,则EC= .
C
4cm
A
B
D
E
达标检测
2.如图,在 ABCD中,DE⊥AB,BF⊥CD,垂足分别是E,F.求证:AE=CF.
证明: ∵四边形ABCD是平行四边形,
∴ ∠A= ∠C,AD=CB.
又∠AED= ∠CFB=90°,
∴ △ADE≌△CBF(AAS),
∴AE=CF.
D
A
B
C
F
E
达标检测
3.在 ABCD中,E、F是AC上的两点,AE=CF,求证:BE=DF.
A
B
C
D
E
F
∴∠BAE=∠DCF
∵在△ABE 和△CDF中,AB=CD,
∠BAE=∠DCF, AE=CF
∴△ABE≌△CDF(SAS), BE=DF
证明: ∵在 ABCD中,AB//CD
达标检测
4.如图,在 ABCD中,E,F是直线BD上的两点,且DE=BF,求证:AE=CF.
证明: ∵四边形ABCD 是平行四边形
∴ ∠ADB= ∠CBD , AD=CB
∵ E,F是直线BD上的两点
∴ ∠ADE=180 -∠ADB,∠CBF=180 -∠CBD, ∴∠ADE= ∠CBF
A
E
B
C
F
D
∵ 在△ADE和△CBF中,DE=BF,∠ADE=∠CBF,AD=CB.
∴△ADE≌△CBF (SAS), AE=CF.
达标检测
达标检测
5.
达标检测
6.
达标检测
7.
达标检测
https://www.21cnjy.com/help/help_extract.php
