19.1.2 矩形的判定 课件(26张ppt)
文档属性
| 名称 | 19.1.2 矩形的判定 课件(26张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-22 11:10:13 | ||
图片预览






文档简介
2022年春华师大版数学
八年级下册数学精品课件
19.1.2 矩形的判定
学习目标
经历矩形判定定理的猜想与证明过程,理解并掌握矩形的判定定理.
能应用矩形的判定解决简单的证明题和计算题.
四边形
平行
四边形
两组对边
分别平行
一个角
是直角
∟
矩形
定义:有一个角是直角的平行四边形叫做矩形.
矩形的性质:
边:对边平行且相等.
角:对角相等; 邻角互补; 四个角都是直角.
对角线:相等且互相平分.
复习回顾
思考:工人师傅在做门窗或矩形零件时,如何确保图形是矩形呢?现在师傅带了两种工具(卷尺和量角器),他说用这两种工具的任意一种就可以解决问题,这是为什么呢?
这节课我们一起探讨矩形的判定吧.
情境引入
类比平行四边形的定义也是判定平行四边形的一种方法,那么矩形的定义也是判定矩形的一种方法.
知识精讲
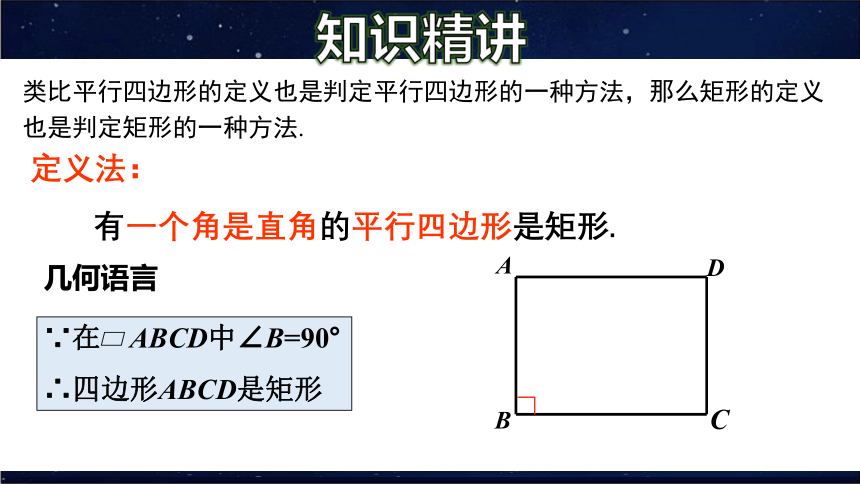
定义法:
有一个角是直角的平行四边形是矩形.
∵在 ABCD中∠B=90°
∴四边形ABCD是矩形
A
B
C
D
∟
几何语言
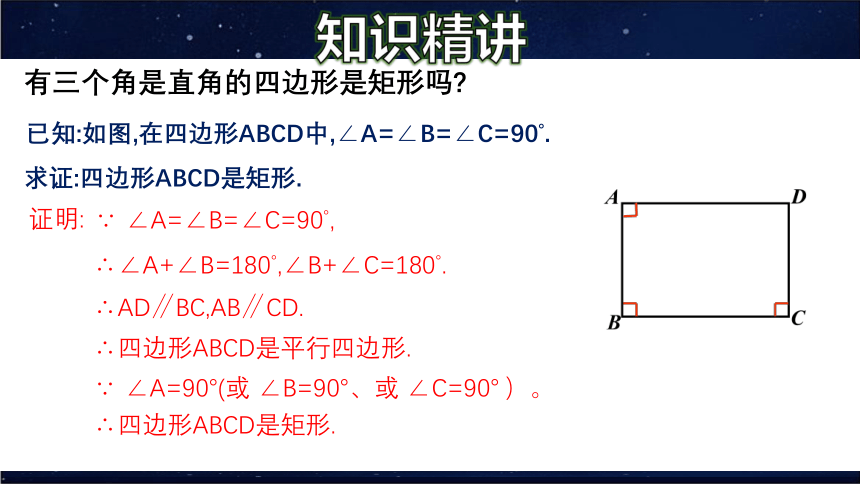
有三个角是直角的四边形是矩形吗?
已知:如图,在四边形ABCD中,∠A=∠B=∠C=90°.
证明:
∵ ∠A=∠B=∠C=90°,
∴∠A+∠B=180°,∠B+∠C=180°.
∴AD∥BC,AB∥CD.
求证:四边形ABCD是矩形.
∴四边形ABCD是平行四边形.
∴四边形ABCD是矩形.
∵ ∠A=90°(或 ∠B=90°、或 ∠C=90° )。
知识精讲
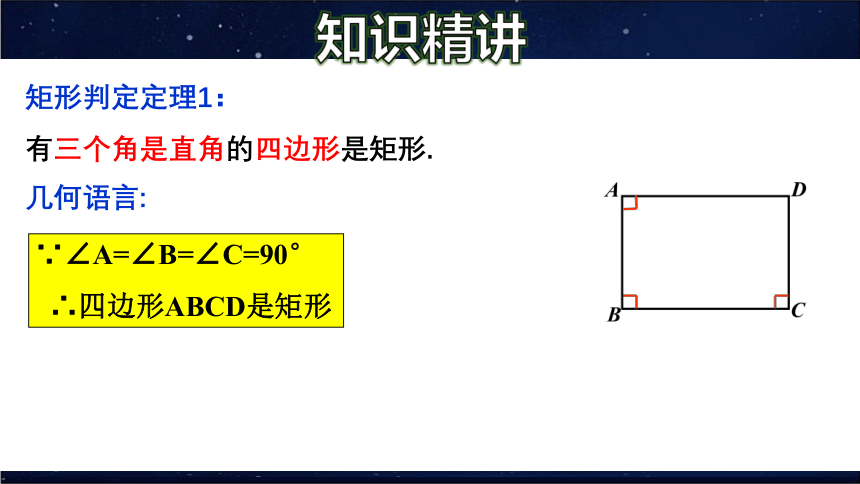
矩形判定定理1:
有三个角是直角的四边形是矩形.
知识精讲
∵∠A=∠B=∠C=90°
∴四边形ABCD是矩形
几何语言:
证明:
在
ABCD中
AB=DC, BD=CA, AD=DA
∴△BAD≌△CDA(SSS)
∴∠BAD=∠CDA
∵AB∥CD
∴∠BAD +∠CDA=180°
∴∠BAD=90°
∴四边形ABCD是矩形
思考:对角线相等的平行四边形是矩形吗?
已知:四边形ABCD是平行四边形,AC=BD.
求证:四边形ABCD是矩形.
(有一个内角是直角的平行四边形是矩形)
知识精讲
A
D
C
B
O
矩形判定定理2:
对角线相等的平行四边形是矩形.
几何语言:
∵四边形ABCD是平行四边形
AC=BD
∴四边形ABCD是矩形
(对角线相等且互相平分的四边形是矩形.)
A
B
C
D
O
(或OA=OC=OB=OD)
知识精讲
1.矩形具有而平行四边形不具有的性质( )
A.内角和是360度 B.对角相等 C.对边平行且相等 D.对角线相等
2.下面性质中,矩形不一定具有的是( )
A.对角线相等 B.四个角相等 C.是轴对称图形 D.对角线垂直
D
D
针对练习
3.判断题:
对角线相等的四边形是矩形。( )
对角线互相平分且相等的四边形是矩形。( )
有一个角是直角的四边形是矩形。( )
四个角都是直角的四边形是矩形。( )
四个角都相等的四边形是矩形。( )
对角线相等且互相垂直的四边形是矩形。( )
针对练习
例1 已知,如图.矩形ABCD的对角线AC、BD相交于点O,且E、F、G、H分别是AO、BO、CO、DO上的一点 ,且AE=BF=CG=DH.求证四边形EFGH是矩形.
证明:
∵四边形ABCD是矩形
∴AC=BD(矩形的对角线相等)
AO=BO=CO=DO(矩形的对角线互相平分)
∵ AE=BF=CG=DH
∴OE=OF=OG=OH
∴四边形EFGH是平行四边形(对角线
互相平分的四边形是平行四边形)
∵EO+OG=FO+OH
即EG=FH
∴四边形EFGH是矩形(对角线相等的平行四边形是矩形)
B
C
D
E
F
G
H
O
A
典例解析
如图,平行四边形ABCD中,∠1=∠2.求证四边形ABCD矩形.
证明:∵四边形ABCD是平行四边形
∴AO=CO,BO=DO
(平行四边形对角线互相平分)
∵ ∠1=∠2
∴AO=BO(等角对等边 )
∴AC=BD
∴四边形ABCD是矩形
(对角线相等的平行四边形是矩形)
针对练习
例2 如图,□?ABCD的四个内角的平分线分别相交于E、F、G、H,求证:四边形 EFGH为矩形.
证明:在□?ABCD中,AD∥BC,
∴∠DAB+∠ABC=180°.
∵AE与BG分别为∠DAB、
∠ABC的平分线,
A
B
D
C
H
E
F
G
∴四边形EFGH是矩形.
同理可证∠AED=∠EHG=90°,
∴∠AFB=90°,
∴∠GFE=90°.
∴ ∠BAE+ ∠ABF= ∠DAB+ ∠ABC=90°.
典例解析
例3 如图,在△ABC中,AB=AC,AD⊥BC,垂足为D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为E,求证:四边形ADCE为矩形.
证明:在△ABC中,AB=AC,AD⊥BC,
∴∠BAD=∠DAC,即∠DAC= ∠BAC.
又∵AN是△ABC外角∠CAM的平分线,
∴∠MAE=∠CAE= ∠CAM,
∴∠DAE=∠DAC+∠CAE
= (∠BAC+∠CAM)=90°.
又∵AD⊥BC,CE⊥AN,
∴∠ADC=∠CEA=90°,
∴四边形ADCE为矩形.
典例解析
现在你可以帮助木工朋友检测所制作的窗框是否是矩形了吧,你可以测量哪些数据,有几种方案,根据又是什么呢?
分别测量出两组对边的长度和一个内角的度数,如果两组对边的长度分别相等,且这个内角是直角,则窗框符合规格.
测量出三个内角的度数,如果三个内角都是直角,则窗框符合规格.
分别测量出窗框四边和两条对角线的长度,如果窗框两组对边长度、两条对角线的长度分别相等,那么窗框符合规格.
方案一:
方案二:
方案三:
问题解决
1.如图,在平行四边形ABCD中,AB=6, BC=8, AC=10.
求证四边形ABCD是矩形.
证明:∵ AB=6,BC=8,AC=10
且62+82=102
∴AB2+BC2=AC2
∴ ∠B=900(勾股定理逆定理 )
∵ ABCD是平行四边形
∴四边形ABCD是矩形
(有一个角是直角的平行四边形是矩形)
达标检测
2. 如图,△ABC中,AB=AC, AD、AE分别是∠A与∠A的外角的平分线,BE⊥AE.求证: AB=DE.
证明:∵AB=AC,AD平分∠BAC
∴AD⊥BC, ∠1= ∠BAC /2
(等腰三角形三线合一)
∵ AE平分∠BAF
∴ ∠2= ∠BAF/2
∵ ∠BAC + ∠BAF=1800
∴ ∠1+ ∠2=(∠BAC + ∠BAF)/2=900
∵ BE⊥AE
∴ ∠BDA= ∠DAE= ∠BEA=900
∴四边形BDAE是矩形(有三个角是直角的四边形是矩形)
1
2
F
达标检测
3.已知:如图, ???ABCD的四个内角的平分线分别相交于E、F、G、H,
求证:四边形 EFGH为矩形.
∴∠GBC+∠GCB=????????×180°=90°
∴∠BGC=90°
同理可证∠AFB=∠AED=90°
∴四边形EFGH是矩形.(有三个角是直角的四边形是矩形)
?
证明:∵AB∥CD
∴∠ABC+∠BCD=180°
∵BG平分∠ABC,CG平分∠BCD ???????????????????????????????????????
达标检测
定理1:有一个角是直角的平行四边形是矩形.
定理2:对角线相等的平行四边形是矩形.
定理3:有三个角是直角的四边形是矩形.
运用定理进行计算和证明
矩形的判定
判定定理
小结梳理
https://www.21cnjy.com/help/help_extract.php
八年级下册数学精品课件
19.1.2 矩形的判定
学习目标
经历矩形判定定理的猜想与证明过程,理解并掌握矩形的判定定理.
能应用矩形的判定解决简单的证明题和计算题.
四边形
平行
四边形
两组对边
分别平行
一个角
是直角
∟
矩形
定义:有一个角是直角的平行四边形叫做矩形.
矩形的性质:
边:对边平行且相等.
角:对角相等; 邻角互补; 四个角都是直角.
对角线:相等且互相平分.
复习回顾
思考:工人师傅在做门窗或矩形零件时,如何确保图形是矩形呢?现在师傅带了两种工具(卷尺和量角器),他说用这两种工具的任意一种就可以解决问题,这是为什么呢?
这节课我们一起探讨矩形的判定吧.
情境引入
类比平行四边形的定义也是判定平行四边形的一种方法,那么矩形的定义也是判定矩形的一种方法.
知识精讲
定义法:
有一个角是直角的平行四边形是矩形.
∵在 ABCD中∠B=90°
∴四边形ABCD是矩形
A
B
C
D
∟
几何语言
有三个角是直角的四边形是矩形吗?
已知:如图,在四边形ABCD中,∠A=∠B=∠C=90°.
证明:
∵ ∠A=∠B=∠C=90°,
∴∠A+∠B=180°,∠B+∠C=180°.
∴AD∥BC,AB∥CD.
求证:四边形ABCD是矩形.
∴四边形ABCD是平行四边形.
∴四边形ABCD是矩形.
∵ ∠A=90°(或 ∠B=90°、或 ∠C=90° )。
知识精讲
矩形判定定理1:
有三个角是直角的四边形是矩形.
知识精讲
∵∠A=∠B=∠C=90°
∴四边形ABCD是矩形
几何语言:
证明:
在
ABCD中
AB=DC, BD=CA, AD=DA
∴△BAD≌△CDA(SSS)
∴∠BAD=∠CDA
∵AB∥CD
∴∠BAD +∠CDA=180°
∴∠BAD=90°
∴四边形ABCD是矩形
思考:对角线相等的平行四边形是矩形吗?
已知:四边形ABCD是平行四边形,AC=BD.
求证:四边形ABCD是矩形.
(有一个内角是直角的平行四边形是矩形)
知识精讲
A
D
C
B
O
矩形判定定理2:
对角线相等的平行四边形是矩形.
几何语言:
∵四边形ABCD是平行四边形
AC=BD
∴四边形ABCD是矩形
(对角线相等且互相平分的四边形是矩形.)
A
B
C
D
O
(或OA=OC=OB=OD)
知识精讲
1.矩形具有而平行四边形不具有的性质( )
A.内角和是360度 B.对角相等 C.对边平行且相等 D.对角线相等
2.下面性质中,矩形不一定具有的是( )
A.对角线相等 B.四个角相等 C.是轴对称图形 D.对角线垂直
D
D
针对练习
3.判断题:
对角线相等的四边形是矩形。( )
对角线互相平分且相等的四边形是矩形。( )
有一个角是直角的四边形是矩形。( )
四个角都是直角的四边形是矩形。( )
四个角都相等的四边形是矩形。( )
对角线相等且互相垂直的四边形是矩形。( )
针对练习
例1 已知,如图.矩形ABCD的对角线AC、BD相交于点O,且E、F、G、H分别是AO、BO、CO、DO上的一点 ,且AE=BF=CG=DH.求证四边形EFGH是矩形.
证明:
∵四边形ABCD是矩形
∴AC=BD(矩形的对角线相等)
AO=BO=CO=DO(矩形的对角线互相平分)
∵ AE=BF=CG=DH
∴OE=OF=OG=OH
∴四边形EFGH是平行四边形(对角线
互相平分的四边形是平行四边形)
∵EO+OG=FO+OH
即EG=FH
∴四边形EFGH是矩形(对角线相等的平行四边形是矩形)
B
C
D
E
F
G
H
O
A
典例解析
如图,平行四边形ABCD中,∠1=∠2.求证四边形ABCD矩形.
证明:∵四边形ABCD是平行四边形
∴AO=CO,BO=DO
(平行四边形对角线互相平分)
∵ ∠1=∠2
∴AO=BO(等角对等边 )
∴AC=BD
∴四边形ABCD是矩形
(对角线相等的平行四边形是矩形)
针对练习
例2 如图,□?ABCD的四个内角的平分线分别相交于E、F、G、H,求证:四边形 EFGH为矩形.
证明:在□?ABCD中,AD∥BC,
∴∠DAB+∠ABC=180°.
∵AE与BG分别为∠DAB、
∠ABC的平分线,
A
B
D
C
H
E
F
G
∴四边形EFGH是矩形.
同理可证∠AED=∠EHG=90°,
∴∠AFB=90°,
∴∠GFE=90°.
∴ ∠BAE+ ∠ABF= ∠DAB+ ∠ABC=90°.
典例解析
例3 如图,在△ABC中,AB=AC,AD⊥BC,垂足为D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为E,求证:四边形ADCE为矩形.
证明:在△ABC中,AB=AC,AD⊥BC,
∴∠BAD=∠DAC,即∠DAC= ∠BAC.
又∵AN是△ABC外角∠CAM的平分线,
∴∠MAE=∠CAE= ∠CAM,
∴∠DAE=∠DAC+∠CAE
= (∠BAC+∠CAM)=90°.
又∵AD⊥BC,CE⊥AN,
∴∠ADC=∠CEA=90°,
∴四边形ADCE为矩形.
典例解析
现在你可以帮助木工朋友检测所制作的窗框是否是矩形了吧,你可以测量哪些数据,有几种方案,根据又是什么呢?
分别测量出两组对边的长度和一个内角的度数,如果两组对边的长度分别相等,且这个内角是直角,则窗框符合规格.
测量出三个内角的度数,如果三个内角都是直角,则窗框符合规格.
分别测量出窗框四边和两条对角线的长度,如果窗框两组对边长度、两条对角线的长度分别相等,那么窗框符合规格.
方案一:
方案二:
方案三:
问题解决
1.如图,在平行四边形ABCD中,AB=6, BC=8, AC=10.
求证四边形ABCD是矩形.
证明:∵ AB=6,BC=8,AC=10
且62+82=102
∴AB2+BC2=AC2
∴ ∠B=900(勾股定理逆定理 )
∵ ABCD是平行四边形
∴四边形ABCD是矩形
(有一个角是直角的平行四边形是矩形)
达标检测
2. 如图,△ABC中,AB=AC, AD、AE分别是∠A与∠A的外角的平分线,BE⊥AE.求证: AB=DE.
证明:∵AB=AC,AD平分∠BAC
∴AD⊥BC, ∠1= ∠BAC /2
(等腰三角形三线合一)
∵ AE平分∠BAF
∴ ∠2= ∠BAF/2
∵ ∠BAC + ∠BAF=1800
∴ ∠1+ ∠2=(∠BAC + ∠BAF)/2=900
∵ BE⊥AE
∴ ∠BDA= ∠DAE= ∠BEA=900
∴四边形BDAE是矩形(有三个角是直角的四边形是矩形)
1
2
F
达标检测
3.已知:如图, ???ABCD的四个内角的平分线分别相交于E、F、G、H,
求证:四边形 EFGH为矩形.
∴∠GBC+∠GCB=????????×180°=90°
∴∠BGC=90°
同理可证∠AFB=∠AED=90°
∴四边形EFGH是矩形.(有三个角是直角的四边形是矩形)
?
证明:∵AB∥CD
∴∠ABC+∠BCD=180°
∵BG平分∠ABC,CG平分∠BCD ???????????????????????????????????????
达标检测
定理1:有一个角是直角的平行四边形是矩形.
定理2:对角线相等的平行四边形是矩形.
定理3:有三个角是直角的四边形是矩形.
运用定理进行计算和证明
矩形的判定
判定定理
小结梳理
https://www.21cnjy.com/help/help_extract.php
