19.3 正方形 课件(共26张PPT)
文档属性
| 名称 | 19.3 正方形 课件(共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-22 09:22:39 | ||
图片预览





文档简介
(共26张PPT)
2022年春华师大版数学
八年级下册数学精品课件
19.3 正方形
学习目标
探索并证明正方形的性质和判定定理,并了解平行四边形、矩形、菱形之间的联系和区别.
会应用正方形的性质和判定定理解决相关证明及计算问题.
菱形的性质
菱形的性质
边:
四条边相等
对角线:
互相垂直平分
分别平分两组对角
角:
具有平行四边形一切性质
对角相等,邻角互补
复习回顾
复习回顾
平行四边形有哪些性质 矩形与平行四边形比较有哪些特殊的性质
平行四边形
边:
角:
对角线:
对边平行且相等
对角相等,邻角互补
对角线互相平分
矩形
角:
四个角是直角
对角线:
对角线相等且互相平分
边:
对边平行且相等
矩 形
〃
〃
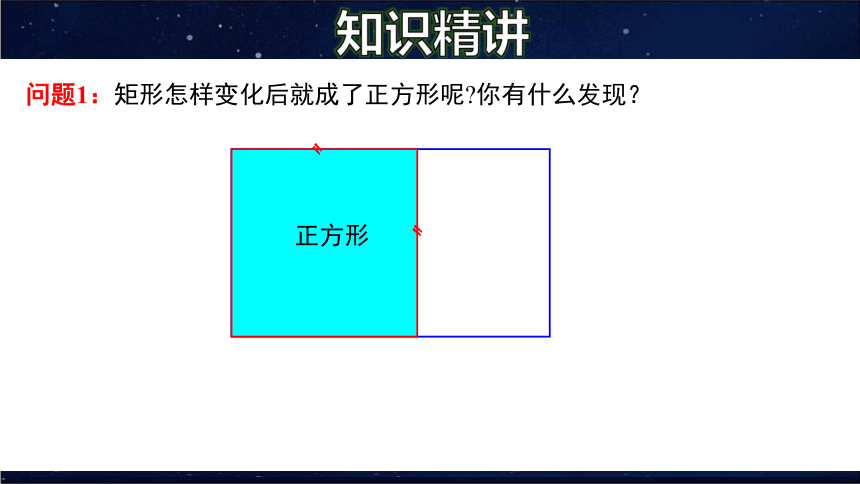
问题1:矩形怎样变化后就成了正方形呢 你有什么发现?
正方形
知识精讲
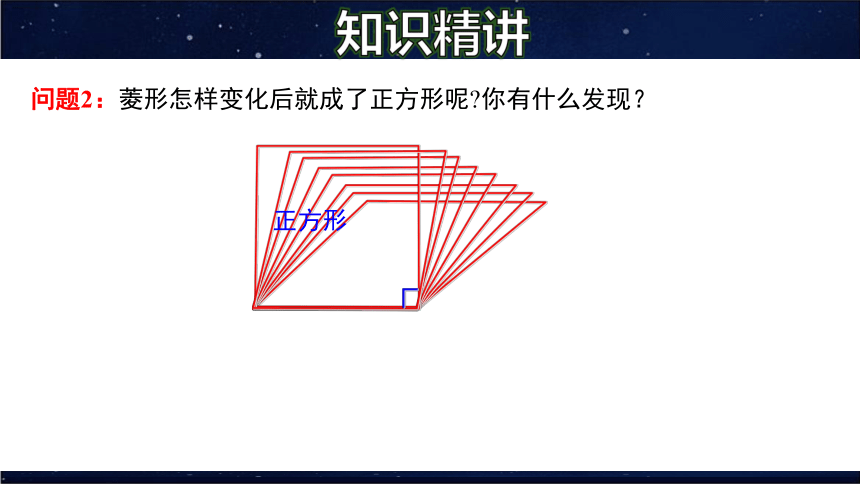
问题2:菱形怎样变化后就成了正方形呢 你有什么发现?
正方形
知识精讲
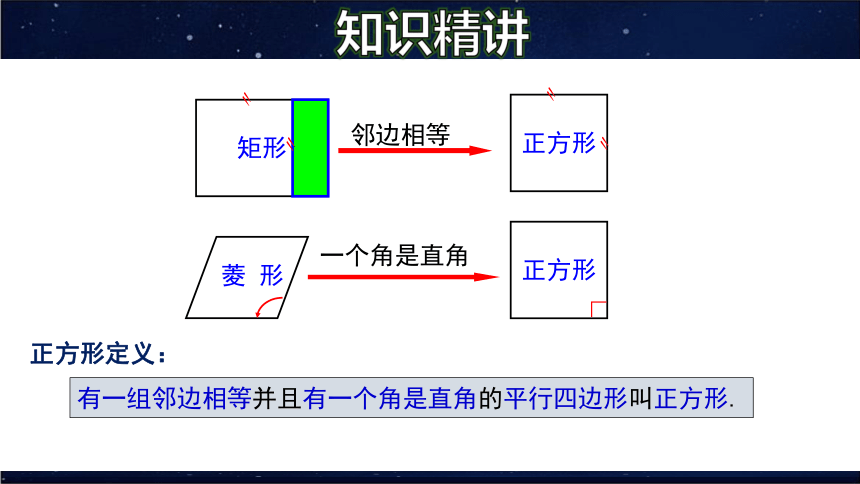
邻边相等
矩形
〃
〃
正方形
〃
〃
菱 形
一个角是直角
正方形
∟
正方形定义:
有一组邻边相等并且有一个角是直角的平行四边形叫正方形.
知识精讲
定义法
菱形法
矩形法
(1)有一组邻边相等且有一个角是直角的的平行四边形是正方形.
(2)有一个角是直角的菱形是正方形.
(3)有一组邻边相等的矩形是正方形.
正方形是特殊的平行四边形,也是特殊的矩形,也是特殊的菱形.
知识精讲
正方形是中心对称图形,对称中心为点O.
它也是轴对称图形,有4条对称轴.
(1)它具有平行四边形的一切性质
两组对边分别平行且相等,两组对角相等,对角线互相平分.
(2)具有矩形的一切性质
四个角都是直角,对角线相等.
(3)具有菱形的一切性质
四条边相等;对角线互相垂直,每条对角线平分一组对角.
O
A
B
C
D
(A)
(B)
(C)
(D)
对称性
特殊性质
知识精讲
1.正方形ABCD,对角线交于0,
(1)若AB=2 ㎝,则AC=________,OA=_________,周长=______,面积=_______.
(2)若OB=2 ㎝,则AC=_______,AB=__________,周长=__________,
面积=__________.
(3)若AC+BD=8 ㎝,则AC=_______,AB=___________,正方形面积=_________.
2.已知正方形的面积为9 cm,它的周长为 _______.
3.正方形的边长为a,当边长增加1时,其面积增加了_______.
O
A
B
C
D
针对练习
2 cm
cm
8 cm
4 cm2
4 cm
2 cm
8 cm2
8 cm
12 cm
4 cm
2 cm
8 cm2
2a+1
你能从这个变化过程中总结出一种正方形的判定方法吗?
边相等
有一组邻
操作1:你能否利用手中的矩形白纸裁出一个正方形呢?请你与同学交流一下,你能说说矩形与正方形的关系吗?
总结:矩形+( )=正方形
判定方法:有一组邻边相等的矩形是正方形.
知识精讲
判定方法:有一个角是直角的菱形是正方形.
是直角
有一个角
操作2:你能否利用手中的可以活动的菱形模型变成一个正方形吗?如何变?
总结:菱形+( )=正方形
你能从这个变化过程中总结出一种正方形的判定方法吗?
知识精讲
判定方法:有一个角是直角一组邻边相等的平行四边形叫做正方形.
边相等
有一组邻
是直角
有一个角
思考:如果是平行四边形呢?
( )+ ( )+平行四边形=正方形.
边相等
有一组邻
是直角
有一个角
你能从这个变化过程中总结出一种正方形的判定方法吗?
知识精讲
例1 如图,在正方形ABCD中, ΔBEC是等边三角形.求证: ∠EAD=∠EDA=15° .
证明:∵ ΔBEC是等边三角形,
∴BE=CE=BC,∠EBC=∠ECB=60°,
∵ 四边形ABCD是正方形,
∴AB=BC=CD,∠ABC=∠DCB=90°,
∴AB=BE=CE=CD, ∠ABE= ∠DCE=30°,
∴△ABE,△DCE是等腰三角形,
∴∠BAE= ∠BEA= ∠CDE= ∠CED=75°,
∴∠EAD= ∠EDA=90°-75°=15°.
典例解析
四边形ABCD是正方形,以正方形ABCD的一边作等边△ADE,求∠BEC的大小.
解:当等边△ADE在正方形ABCD外部时,如图①,
AB=AE,∠BAE=90°+60°=150°.
∴∠AEB=15°.
同理可得∠DEC=15°.
∴∠BEC=60°-15°-15°=30°;
针对练习
当等边△ADE在正方形ABCD内部时,如图②,
AB=AE,∠BAE=90°-60°=30°,
∴∠AEB=75°.
同理可得∠DEC=75°.
∴∠BEC=360°-75°-75°-60°=150°.
综上所述,∠BEC的大小为30°或150°.
【点睛】因为等边△ADE与正方形ABCD有一条公共边,所以边相等.本题分两种情况:等边△ADE在正方形的外部或在正方形的内部.
针对练习
例2 如图,在正方形ABCD中,P为BD上一点,PE⊥BC于E, PF⊥DC于F.试说明:AP=EF.
A
B
C
D
P
E
F
解:
连接PC,AC.
又∵PE⊥BC , PF⊥DC,
∵四边形ABCD是正方形,
∴∠FCE=90°, AC垂直平分BD,
∴四边形PECF是矩形,
∴PC=EF.
∴AP=PC.
∴AP=EF.
【点睛】在正方形的条件下证明两条线段相等:通常连接对角线构造垂直平分的模型,利用垂直平分线性质,角平分线性质,等腰三角形等来说明.
典例解析
例3 在正方形ABCD中,点E、F、M、N分别在各边上,且AE=BF=CM=DN.四边形EFMN是正方形吗 为什么
证明:∵四边形ABCD是正方形,
∴AB=BC=CD=DA,∠A=∠B=∠C=∠D=90°.
∵AE=BF=CM=DN,
∴AN=BE=CF=DM.
分析:由已知可证△AEN≌△BFE≌△CMF≌△DNM,得四边形EFMN是菱形,再证有一个角是直角即可.
典例解析
在△AEN、△BFE、△CMF、△DNM中,
AE=BF=CM=DN,
∠A=∠B=∠C=∠D,
AN=BE=CF=DM,
∴△AEN≌△BFE≌△CMF≌△DNM,
∴EN=FE=MF=NM,∠ANE=∠BEF,
∴四边形EFMN是菱形,
∠NEF=180°-(∠AEN+∠BEF)
=180°-(∠AEN+∠ANE)
=180°-90°=90°.
∴四边形EFMN是正方形 .
典例解析
证明:∵ DE⊥AC,DF⊥AB ,
∴∠DEC= ∠DFC=90°.
又∵ ∠C=90 °,
∴四边形ADFC是矩形.
过点D作DG⊥AB,垂足为G.
∵AD是∠CAB的平分线
DE⊥AC,DG⊥AB,
∴ DE=DG.
同理得DG=DF,
∴ED=DF,
∴四边形ADFC是正方形.
例4 如图,在直角三角形中,∠C=90°,∠A、∠B的平分线交于点D.
DE⊥AC,DF⊥AB.求证:四边形CEDF为正方形.
A
B
C
D
E
F
G
典例解析
例5 如图,EG,FH过正方形ABCD的对角线的交点O,且EG⊥FH.求证:四边形EFGH是正方形.
证明:∵四边形ABCD为正方形,
∴OB=OC,∠ABO=∠BCO =45°,
∠BOC=90°=∠COH+∠BOH.
∵EG⊥FH,
∴∠BOE+∠BOH=90°,
∴∠COH=∠BOE,
∴△CHO ≌△BEO,∴OE=OH.
同理可证:OE=OF=OG,
B
A
C
D
O
E
H
G
F
典例解析
∴OE=OF=OG=OH.
又∵EG⊥FH,
∴四边形EFGH为菱形.
∵EO+GO=FO+HO ,即EG=HF,
∴四边形EFGH为正方形.
B
A
C
B
O
E
H
G
F
典例解析
5种识
别方法
三个角是直角
四条边相等
一个角是直角
或对角线相等
一组邻边相等
或对角线垂直
一组邻边相等
或对角线垂直
一个角是直角
或对角线相等
一个角是直角且一组邻边相等
平行四边形、矩形、菱形、正方形的判定小结
每条对角线都平分一组对角
小结梳理
https://www.21cnjy.com/help/help_extract.php
2022年春华师大版数学
八年级下册数学精品课件
19.3 正方形
学习目标
探索并证明正方形的性质和判定定理,并了解平行四边形、矩形、菱形之间的联系和区别.
会应用正方形的性质和判定定理解决相关证明及计算问题.
菱形的性质
菱形的性质
边:
四条边相等
对角线:
互相垂直平分
分别平分两组对角
角:
具有平行四边形一切性质
对角相等,邻角互补
复习回顾
复习回顾
平行四边形有哪些性质 矩形与平行四边形比较有哪些特殊的性质
平行四边形
边:
角:
对角线:
对边平行且相等
对角相等,邻角互补
对角线互相平分
矩形
角:
四个角是直角
对角线:
对角线相等且互相平分
边:
对边平行且相等
矩 形
〃
〃
问题1:矩形怎样变化后就成了正方形呢 你有什么发现?
正方形
知识精讲
问题2:菱形怎样变化后就成了正方形呢 你有什么发现?
正方形
知识精讲
邻边相等
矩形
〃
〃
正方形
〃
〃
菱 形
一个角是直角
正方形
∟
正方形定义:
有一组邻边相等并且有一个角是直角的平行四边形叫正方形.
知识精讲
定义法
菱形法
矩形法
(1)有一组邻边相等且有一个角是直角的的平行四边形是正方形.
(2)有一个角是直角的菱形是正方形.
(3)有一组邻边相等的矩形是正方形.
正方形是特殊的平行四边形,也是特殊的矩形,也是特殊的菱形.
知识精讲
正方形是中心对称图形,对称中心为点O.
它也是轴对称图形,有4条对称轴.
(1)它具有平行四边形的一切性质
两组对边分别平行且相等,两组对角相等,对角线互相平分.
(2)具有矩形的一切性质
四个角都是直角,对角线相等.
(3)具有菱形的一切性质
四条边相等;对角线互相垂直,每条对角线平分一组对角.
O
A
B
C
D
(A)
(B)
(C)
(D)
对称性
特殊性质
知识精讲
1.正方形ABCD,对角线交于0,
(1)若AB=2 ㎝,则AC=________,OA=_________,周长=______,面积=_______.
(2)若OB=2 ㎝,则AC=_______,AB=__________,周长=__________,
面积=__________.
(3)若AC+BD=8 ㎝,则AC=_______,AB=___________,正方形面积=_________.
2.已知正方形的面积为9 cm,它的周长为 _______.
3.正方形的边长为a,当边长增加1时,其面积增加了_______.
O
A
B
C
D
针对练习
2 cm
cm
8 cm
4 cm2
4 cm
2 cm
8 cm2
8 cm
12 cm
4 cm
2 cm
8 cm2
2a+1
你能从这个变化过程中总结出一种正方形的判定方法吗?
边相等
有一组邻
操作1:你能否利用手中的矩形白纸裁出一个正方形呢?请你与同学交流一下,你能说说矩形与正方形的关系吗?
总结:矩形+( )=正方形
判定方法:有一组邻边相等的矩形是正方形.
知识精讲
判定方法:有一个角是直角的菱形是正方形.
是直角
有一个角
操作2:你能否利用手中的可以活动的菱形模型变成一个正方形吗?如何变?
总结:菱形+( )=正方形
你能从这个变化过程中总结出一种正方形的判定方法吗?
知识精讲
判定方法:有一个角是直角一组邻边相等的平行四边形叫做正方形.
边相等
有一组邻
是直角
有一个角
思考:如果是平行四边形呢?
( )+ ( )+平行四边形=正方形.
边相等
有一组邻
是直角
有一个角
你能从这个变化过程中总结出一种正方形的判定方法吗?
知识精讲
例1 如图,在正方形ABCD中, ΔBEC是等边三角形.求证: ∠EAD=∠EDA=15° .
证明:∵ ΔBEC是等边三角形,
∴BE=CE=BC,∠EBC=∠ECB=60°,
∵ 四边形ABCD是正方形,
∴AB=BC=CD,∠ABC=∠DCB=90°,
∴AB=BE=CE=CD, ∠ABE= ∠DCE=30°,
∴△ABE,△DCE是等腰三角形,
∴∠BAE= ∠BEA= ∠CDE= ∠CED=75°,
∴∠EAD= ∠EDA=90°-75°=15°.
典例解析
四边形ABCD是正方形,以正方形ABCD的一边作等边△ADE,求∠BEC的大小.
解:当等边△ADE在正方形ABCD外部时,如图①,
AB=AE,∠BAE=90°+60°=150°.
∴∠AEB=15°.
同理可得∠DEC=15°.
∴∠BEC=60°-15°-15°=30°;
针对练习
当等边△ADE在正方形ABCD内部时,如图②,
AB=AE,∠BAE=90°-60°=30°,
∴∠AEB=75°.
同理可得∠DEC=75°.
∴∠BEC=360°-75°-75°-60°=150°.
综上所述,∠BEC的大小为30°或150°.
【点睛】因为等边△ADE与正方形ABCD有一条公共边,所以边相等.本题分两种情况:等边△ADE在正方形的外部或在正方形的内部.
针对练习
例2 如图,在正方形ABCD中,P为BD上一点,PE⊥BC于E, PF⊥DC于F.试说明:AP=EF.
A
B
C
D
P
E
F
解:
连接PC,AC.
又∵PE⊥BC , PF⊥DC,
∵四边形ABCD是正方形,
∴∠FCE=90°, AC垂直平分BD,
∴四边形PECF是矩形,
∴PC=EF.
∴AP=PC.
∴AP=EF.
【点睛】在正方形的条件下证明两条线段相等:通常连接对角线构造垂直平分的模型,利用垂直平分线性质,角平分线性质,等腰三角形等来说明.
典例解析
例3 在正方形ABCD中,点E、F、M、N分别在各边上,且AE=BF=CM=DN.四边形EFMN是正方形吗 为什么
证明:∵四边形ABCD是正方形,
∴AB=BC=CD=DA,∠A=∠B=∠C=∠D=90°.
∵AE=BF=CM=DN,
∴AN=BE=CF=DM.
分析:由已知可证△AEN≌△BFE≌△CMF≌△DNM,得四边形EFMN是菱形,再证有一个角是直角即可.
典例解析
在△AEN、△BFE、△CMF、△DNM中,
AE=BF=CM=DN,
∠A=∠B=∠C=∠D,
AN=BE=CF=DM,
∴△AEN≌△BFE≌△CMF≌△DNM,
∴EN=FE=MF=NM,∠ANE=∠BEF,
∴四边形EFMN是菱形,
∠NEF=180°-(∠AEN+∠BEF)
=180°-(∠AEN+∠ANE)
=180°-90°=90°.
∴四边形EFMN是正方形 .
典例解析
证明:∵ DE⊥AC,DF⊥AB ,
∴∠DEC= ∠DFC=90°.
又∵ ∠C=90 °,
∴四边形ADFC是矩形.
过点D作DG⊥AB,垂足为G.
∵AD是∠CAB的平分线
DE⊥AC,DG⊥AB,
∴ DE=DG.
同理得DG=DF,
∴ED=DF,
∴四边形ADFC是正方形.
例4 如图,在直角三角形中,∠C=90°,∠A、∠B的平分线交于点D.
DE⊥AC,DF⊥AB.求证:四边形CEDF为正方形.
A
B
C
D
E
F
G
典例解析
例5 如图,EG,FH过正方形ABCD的对角线的交点O,且EG⊥FH.求证:四边形EFGH是正方形.
证明:∵四边形ABCD为正方形,
∴OB=OC,∠ABO=∠BCO =45°,
∠BOC=90°=∠COH+∠BOH.
∵EG⊥FH,
∴∠BOE+∠BOH=90°,
∴∠COH=∠BOE,
∴△CHO ≌△BEO,∴OE=OH.
同理可证:OE=OF=OG,
B
A
C
D
O
E
H
G
F
典例解析
∴OE=OF=OG=OH.
又∵EG⊥FH,
∴四边形EFGH为菱形.
∵EO+GO=FO+HO ,即EG=HF,
∴四边形EFGH为正方形.
B
A
C
B
O
E
H
G
F
典例解析
5种识
别方法
三个角是直角
四条边相等
一个角是直角
或对角线相等
一组邻边相等
或对角线垂直
一组邻边相等
或对角线垂直
一个角是直角
或对角线相等
一个角是直角且一组邻边相等
平行四边形、矩形、菱形、正方形的判定小结
每条对角线都平分一组对角
小结梳理
https://www.21cnjy.com/help/help_extract.php
