北师大版八年级数学下册 5.1分式的认识 课件(共18张PPT)
文档属性
| 名称 | 北师大版八年级数学下册 5.1分式的认识 课件(共18张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 952.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-21 00:00:00 | ||
图片预览




文档简介
(共18张PPT)
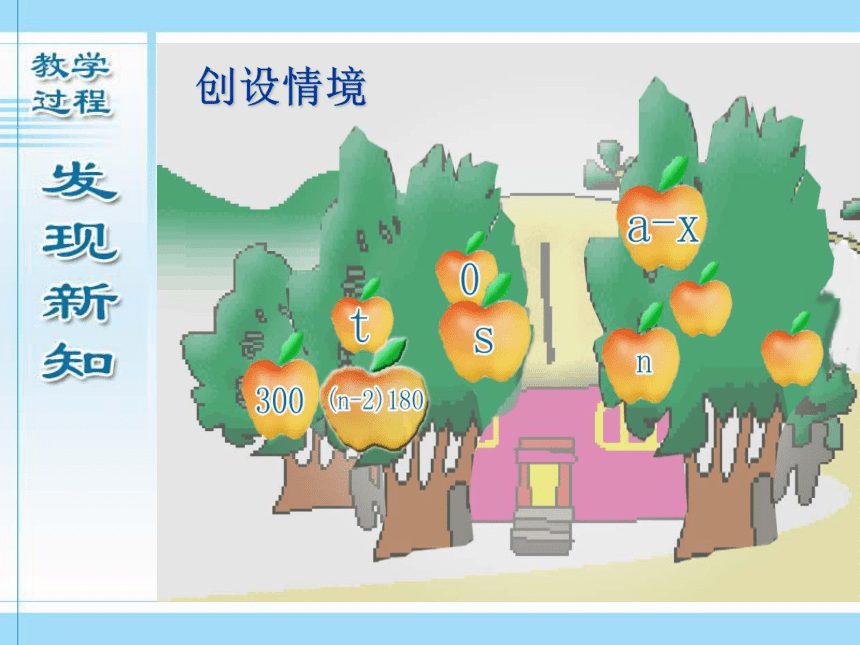
创设情境
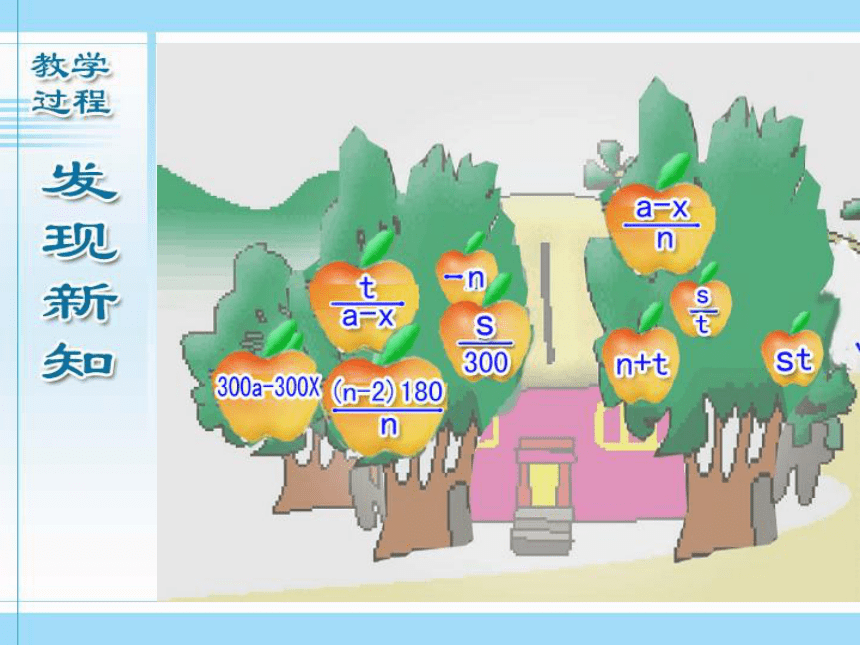
(1)议一议:你们所发现的这一类新代数式: , ,……它 们有 什么共同特征?它们与整式有什么不同?
探索交流
t
s
x
a
n
-
(2)类比分数,概括分式的概念
及表达形式。
探索交流
被除数
除数
3
4
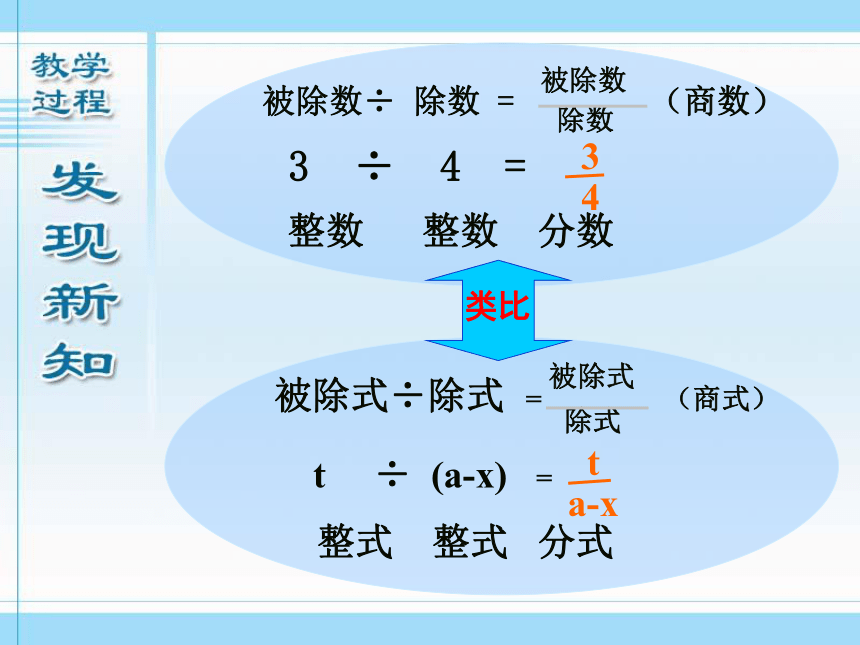
被除数÷ 除数 = (商数)
整数 整数 分数
3 ÷ 4 =
被除式
除式
t
a-x
被除式÷除式 = (商式)
整式 整式 分式
t ÷ (a-x) =
类比
用A、B表示两个整式,A÷B就可以表示成
形式。如果B中含有字母,式子
就叫做分式。 其中,A叫做分式的分子,
B叫做分式的分母。对于任意一个分式,
分母都不能为零。
概括分式概念:
B
A
B
A
(3)小组内互举例子,判定是否分式
探索交流
注意: 与 的本质区别
强调: 中,B中一定要有字母
300
S
S
t
A
B
辨析
分式的概念要素
①分子分母都是整式
②分母中含有字母
③分母不能为零。
填表:
自主探究
a
1
a
a-1
a … -2 -1 0 1
2 …
… …
… …
在分式 里 ,B≠0时分式有意义。
概括:
A
B
分式在什么条件下有意义?
例1
(1)当a=1,2时,分别求分式
的值.
(学生自主完成,同桌交流,师生评述)
(2)a取何值时,分式 有
意义?
2a
a+1
a+1
2a
你知道吗 当x取什么值时,
下列分式有意义?
(小组合作完成,组间抢答,师生评述)
1
2
+
x
y
9
1
2
-
x
练习
1
8
-
x
( 1 )
( 2 )
( 3 )
面对日益严重的土地沙化问题,某县决定分期分批固沙造林,一期工程计划在一定期限内固沙造林2004公顷,实际每月固沙造林的面积比原计划多30公顷,结果提前4个月完成原计划任务。如果设原计划每月固沙造林 x公顷,那么原计划完成一期工程需要( )个月,实际完成一期工程用了( )个月。
例2
1、浙江衢州常山“天子”牌胡柚为了能提前采收,抢占市场,需要给胡柚套袋以更好地吸收光能。已知一个果农一天能完成1200只胡柚的套袋工作,现在n个果农完成m个胡柚的套袋工作需要( )天。
练习
2、(书P109随堂练习3):把甲、乙两种饮料按质量比x:y混合在一起,可以调制成一种混合饮料。调制1千克这种混合饮料需多少甲种饮料?
一个概念
总结
分母等于零
分母不等于零
分子等于零
且分母不等于零
两个应用
列分式
求分式的值
三个条件
分式有意义的条件
分式无意义的条件
分式的值为零的条件
分式的概念
①分子分母都是整式
②分母中含有字母
③分母不能为零。
1、试一试,你能行:
①必做题:书本P58“做一做”
②书本P60习题3.1 (分层布置)
③思考题:书本引例第三问
2、请你联想:
尽可能多地找出你所学过的与分式有关的知识内容(如:已知三角形的面积为S,底边长为a,那么底边上的高线长h为 ),并将它写进你今天的数学小日记。
a
s
2
作业
创设情境
(1)议一议:你们所发现的这一类新代数式: , ,……它 们有 什么共同特征?它们与整式有什么不同?
探索交流
t
s
x
a
n
-
(2)类比分数,概括分式的概念
及表达形式。
探索交流
被除数
除数
3
4
被除数÷ 除数 = (商数)
整数 整数 分数
3 ÷ 4 =
被除式
除式
t
a-x
被除式÷除式 = (商式)
整式 整式 分式
t ÷ (a-x) =
类比
用A、B表示两个整式,A÷B就可以表示成
形式。如果B中含有字母,式子
就叫做分式。 其中,A叫做分式的分子,
B叫做分式的分母。对于任意一个分式,
分母都不能为零。
概括分式概念:
B
A
B
A
(3)小组内互举例子,判定是否分式
探索交流
注意: 与 的本质区别
强调: 中,B中一定要有字母
300
S
S
t
A
B
辨析
分式的概念要素
①分子分母都是整式
②分母中含有字母
③分母不能为零。
填表:
自主探究
a
1
a
a-1
a … -2 -1 0 1
2 …
… …
… …
在分式 里 ,B≠0时分式有意义。
概括:
A
B
分式在什么条件下有意义?
例1
(1)当a=1,2时,分别求分式
的值.
(学生自主完成,同桌交流,师生评述)
(2)a取何值时,分式 有
意义?
2a
a+1
a+1
2a
你知道吗 当x取什么值时,
下列分式有意义?
(小组合作完成,组间抢答,师生评述)
1
2
+
x
y
9
1
2
-
x
练习
1
8
-
x
( 1 )
( 2 )
( 3 )
面对日益严重的土地沙化问题,某县决定分期分批固沙造林,一期工程计划在一定期限内固沙造林2004公顷,实际每月固沙造林的面积比原计划多30公顷,结果提前4个月完成原计划任务。如果设原计划每月固沙造林 x公顷,那么原计划完成一期工程需要( )个月,实际完成一期工程用了( )个月。
例2
1、浙江衢州常山“天子”牌胡柚为了能提前采收,抢占市场,需要给胡柚套袋以更好地吸收光能。已知一个果农一天能完成1200只胡柚的套袋工作,现在n个果农完成m个胡柚的套袋工作需要( )天。
练习
2、(书P109随堂练习3):把甲、乙两种饮料按质量比x:y混合在一起,可以调制成一种混合饮料。调制1千克这种混合饮料需多少甲种饮料?
一个概念
总结
分母等于零
分母不等于零
分子等于零
且分母不等于零
两个应用
列分式
求分式的值
三个条件
分式有意义的条件
分式无意义的条件
分式的值为零的条件
分式的概念
①分子分母都是整式
②分母中含有字母
③分母不能为零。
1、试一试,你能行:
①必做题:书本P58“做一做”
②书本P60习题3.1 (分层布置)
③思考题:书本引例第三问
2、请你联想:
尽可能多地找出你所学过的与分式有关的知识内容(如:已知三角形的面积为S,底边长为a,那么底边上的高线长h为 ),并将它写进你今天的数学小日记。
a
s
2
作业
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
