北师大版八年级数学下册 1.1 等腰三角形 课件(共23张PPT)
文档属性
| 名称 | 北师大版八年级数学下册 1.1 等腰三角形 课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 9.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-21 14:17:52 | ||
图片预览







文档简介
(共23张PPT)
等腰三角形
北师大八下数学
从数学的观点思考你能观察到什么图形
等腰三角形
学习目标
知识与技能:理解等腰三角形的性质,会利用等腰三角形
的性质,进行简单地推理、判断和计算
过程与方法:通过观察、实践、猜想、论证发展学生的推
理能力、动手操作能力和数学语言表达能力
情感态度价值观:在实际操作动手中感受几何应用美
等腰三角形的相关定义
有两条边相等的三角形叫做等腰三角形
相等的两条边叫做腰
另一条边叫做底
底边与腰的夹角叫做底角
两腰所夹的角叫做顶角
边的分类
角的分类
A
B
C
哪两条边
自主学习,同步展示
学习建议:
每个人都带着明确的目标投入课堂。
完成导学案中的内容
(1)性质2中的条件是什么,结论又是什么?
(2)性质3中需要注意什么
做好疑难问题标记,准备讨论或点评解决
目标:
安静、投入、思考、高效
一(1)把你们准备的顶角分别为锐角、直角和钝角的等腰三角形拿出来;
(2)把三角形的顶角顶点记为A,底角顶点记为B,C。
(3)把三角形对折,让两腰AB,AC重叠在一起,折痕为AD。
等腰三角形性质探索
二(1)你如何剪出的等腰三角形?
(2)你发现等腰三角形有哪些特征?
(3)尝试用语言表达出来
等腰三角形的性质
等腰三角形性质1 等腰三角形是轴对称图形
等腰三角形性质2 等腰三角形的顶角平分线、底边上的中线和底边上的高
互相重合,简称“三线合一”它们所在的直线都是等腰三角形的对称轴
等腰三角形性质3 等腰三角形的两个底角相等(简写“等边对等角”)
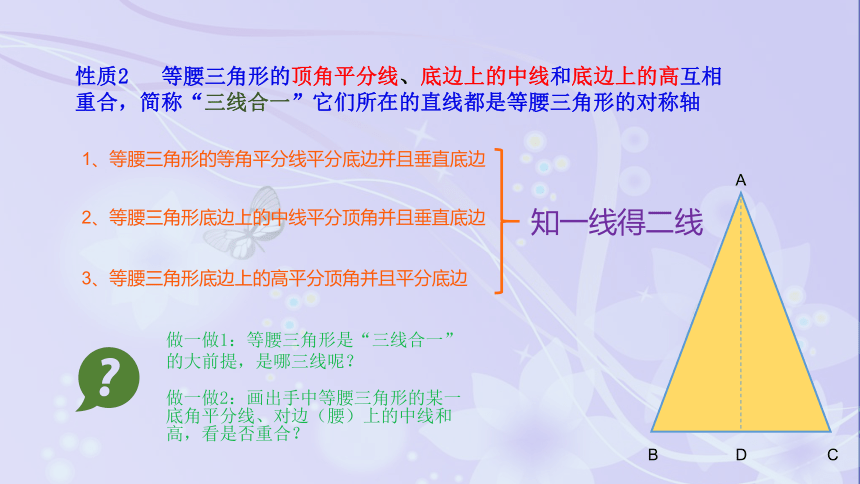
性质2 等腰三角形的顶角平分线、底边上的中线和底边上的高互相
重合,简称“三线合一”它们所在的直线都是等腰三角形的对称轴
1、等腰三角形的等角平分线平分底边并且垂直底边
2、等腰三角形底边上的中线平分顶角并且垂直底边
3、等腰三角形底边上的高平分顶角并且平分底边
A
B
C
D
做一做1:等腰三角形是“三线合一”
的大前提,是哪三线呢?
做一做2:画出手中等腰三角形的某一
底角平分线、对边(腰)上的中线和
高,看是否重合?
知一线得二线
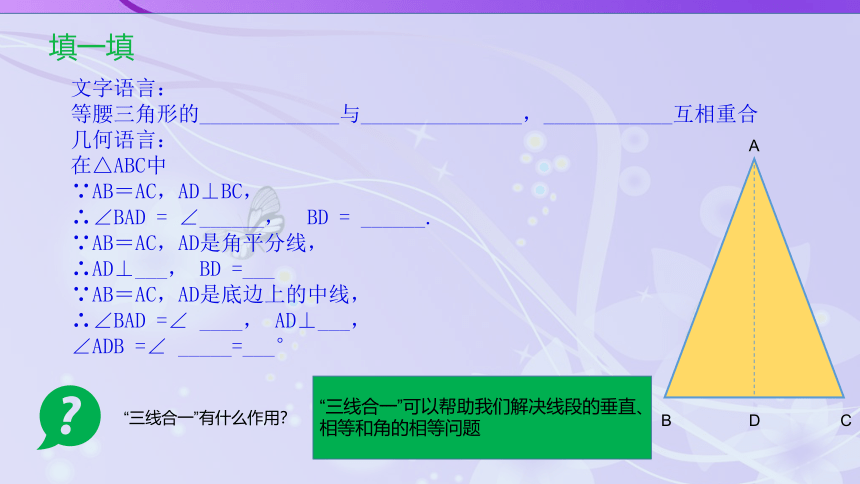
填一填
文字语言:
等腰三角形的_____________与_______________,____________互相重合
几何语言:
在△ABC中
∵AB=AC,AD⊥BC,
∴∠BAD = ∠______, BD = ______.
∵AB=AC,AD是角平分线,
∴AD⊥___, BD =___
∵AB=AC,AD是底边上的中线,
∴∠BAD =∠ ____, AD⊥___,
∠ADB =∠ _____=___°
A
B
C
D
“三线合一”有什么作用?
“三线合一”可以帮助我们解决线段的垂直、
相等和角的相等问题
性质3 等腰三角形的两个底角相等。简写成:等边对等角
几何语言:
如图,在△ABC中,
∵AB=AC(已知),
∴∠B=∠C(等边对等角).
A
B
C
如何证明等腰三角形的两个底角相等
注意:在一个三角形中,等边对等角
那么这个性质有什么作用呢?
一. 遇角需讨论
例1. (1)已知等腰三角形的一个内角为75°则其顶角为( )
A. 30° B. 75°
C. 105° D. 30°或75°
(2)、已知等腰三角形的一个角是100度,则底角等于_____________
二、遇边需讨论
例2. 已知等腰三角形的一边等于5,另一边等于6,则它的周长等
于_________。
练一练
例1 已知:如图,在△ABC中,AB=AC.点D在AC上,且AD=DB=BC,求 ABC各角度数
A
B
C
D
分析:图中有哪些等腰三角形?
有哪些相等的角?
分析顺序是什么?
方程思想
代数方法
几何问题
例2 已知:如图,在△ABC中,点D,E在边BC上,AB=AC,AD=AE,
求证:BD=CE
A
B
C
D
E
方法:求有关等腰三角形问题时,顶角平分线、
底边上的高、底边上的中线是常用的辅助线
总结
1.知识方面
等腰三角
形的特征
①从边看——两边相等
②从角看——两个底角相等
③从“三线”看——顶角平分线、底边上的高、
底边上的中线(三线合一)
④从“整体”看——轴对称图形
2.方法方面
①分类思想,方程思想
②等腰三角形常用辅助线
顶角平分线、底边上的高、底边上的中线
A、B是4×4网格中的格点,网格中的每个小正方形的边长为1,请在图中清晰标出使以A、B、C为顶点的三角形是等腰三角形的所有格点C的位置.
找一找
A
B
C1
C2
C3
C4
C5
C6
C7
C8
8个
怎样做到
不重复不
遗漏
如图,在△ABC中,AC=BC , ∠ACB=90°,D是AC上一点,AE⊥BD交BD的延长线于E,BD是∠ABC的角平分线
求证:AE= BD
欣赏美丽的图片,感受等腰三角形在现实生活
中的应用,感受它的对称美
鹳雀楼
等腰三角形的屋顶是我国古代建筑经常
采用的建筑形式
世界建筑中的等腰三角形
因为三角形不容易变形,具有稳定性,所以建筑中采用的很多;还因为具有轴对称性,具有对称美
为什么建筑设计中常有等腰三角形?
家居生活中的等腰三角形
邮票中的等腰三角形
随处可见的等腰三角形
谢谢
等腰三角形
北师大八下数学
从数学的观点思考你能观察到什么图形
等腰三角形
学习目标
知识与技能:理解等腰三角形的性质,会利用等腰三角形
的性质,进行简单地推理、判断和计算
过程与方法:通过观察、实践、猜想、论证发展学生的推
理能力、动手操作能力和数学语言表达能力
情感态度价值观:在实际操作动手中感受几何应用美
等腰三角形的相关定义
有两条边相等的三角形叫做等腰三角形
相等的两条边叫做腰
另一条边叫做底
底边与腰的夹角叫做底角
两腰所夹的角叫做顶角
边的分类
角的分类
A
B
C
哪两条边
自主学习,同步展示
学习建议:
每个人都带着明确的目标投入课堂。
完成导学案中的内容
(1)性质2中的条件是什么,结论又是什么?
(2)性质3中需要注意什么
做好疑难问题标记,准备讨论或点评解决
目标:
安静、投入、思考、高效
一(1)把你们准备的顶角分别为锐角、直角和钝角的等腰三角形拿出来;
(2)把三角形的顶角顶点记为A,底角顶点记为B,C。
(3)把三角形对折,让两腰AB,AC重叠在一起,折痕为AD。
等腰三角形性质探索
二(1)你如何剪出的等腰三角形?
(2)你发现等腰三角形有哪些特征?
(3)尝试用语言表达出来
等腰三角形的性质
等腰三角形性质1 等腰三角形是轴对称图形
等腰三角形性质2 等腰三角形的顶角平分线、底边上的中线和底边上的高
互相重合,简称“三线合一”它们所在的直线都是等腰三角形的对称轴
等腰三角形性质3 等腰三角形的两个底角相等(简写“等边对等角”)
性质2 等腰三角形的顶角平分线、底边上的中线和底边上的高互相
重合,简称“三线合一”它们所在的直线都是等腰三角形的对称轴
1、等腰三角形的等角平分线平分底边并且垂直底边
2、等腰三角形底边上的中线平分顶角并且垂直底边
3、等腰三角形底边上的高平分顶角并且平分底边
A
B
C
D
做一做1:等腰三角形是“三线合一”
的大前提,是哪三线呢?
做一做2:画出手中等腰三角形的某一
底角平分线、对边(腰)上的中线和
高,看是否重合?
知一线得二线
填一填
文字语言:
等腰三角形的_____________与_______________,____________互相重合
几何语言:
在△ABC中
∵AB=AC,AD⊥BC,
∴∠BAD = ∠______, BD = ______.
∵AB=AC,AD是角平分线,
∴AD⊥___, BD =___
∵AB=AC,AD是底边上的中线,
∴∠BAD =∠ ____, AD⊥___,
∠ADB =∠ _____=___°
A
B
C
D
“三线合一”有什么作用?
“三线合一”可以帮助我们解决线段的垂直、
相等和角的相等问题
性质3 等腰三角形的两个底角相等。简写成:等边对等角
几何语言:
如图,在△ABC中,
∵AB=AC(已知),
∴∠B=∠C(等边对等角).
A
B
C
如何证明等腰三角形的两个底角相等
注意:在一个三角形中,等边对等角
那么这个性质有什么作用呢?
一. 遇角需讨论
例1. (1)已知等腰三角形的一个内角为75°则其顶角为( )
A. 30° B. 75°
C. 105° D. 30°或75°
(2)、已知等腰三角形的一个角是100度,则底角等于_____________
二、遇边需讨论
例2. 已知等腰三角形的一边等于5,另一边等于6,则它的周长等
于_________。
练一练
例1 已知:如图,在△ABC中,AB=AC.点D在AC上,且AD=DB=BC,求 ABC各角度数
A
B
C
D
分析:图中有哪些等腰三角形?
有哪些相等的角?
分析顺序是什么?
方程思想
代数方法
几何问题
例2 已知:如图,在△ABC中,点D,E在边BC上,AB=AC,AD=AE,
求证:BD=CE
A
B
C
D
E
方法:求有关等腰三角形问题时,顶角平分线、
底边上的高、底边上的中线是常用的辅助线
总结
1.知识方面
等腰三角
形的特征
①从边看——两边相等
②从角看——两个底角相等
③从“三线”看——顶角平分线、底边上的高、
底边上的中线(三线合一)
④从“整体”看——轴对称图形
2.方法方面
①分类思想,方程思想
②等腰三角形常用辅助线
顶角平分线、底边上的高、底边上的中线
A、B是4×4网格中的格点,网格中的每个小正方形的边长为1,请在图中清晰标出使以A、B、C为顶点的三角形是等腰三角形的所有格点C的位置.
找一找
A
B
C1
C2
C3
C4
C5
C6
C7
C8
8个
怎样做到
不重复不
遗漏
如图,在△ABC中,AC=BC , ∠ACB=90°,D是AC上一点,AE⊥BD交BD的延长线于E,BD是∠ABC的角平分线
求证:AE= BD
欣赏美丽的图片,感受等腰三角形在现实生活
中的应用,感受它的对称美
鹳雀楼
等腰三角形的屋顶是我国古代建筑经常
采用的建筑形式
世界建筑中的等腰三角形
因为三角形不容易变形,具有稳定性,所以建筑中采用的很多;还因为具有轴对称性,具有对称美
为什么建筑设计中常有等腰三角形?
家居生活中的等腰三角形
邮票中的等腰三角形
随处可见的等腰三角形
谢谢
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
