2021--2022学年人教版八年级数学下册第二十章数据的分析单元测试(Word版含答案)
文档属性
| 名称 | 2021--2022学年人教版八年级数学下册第二十章数据的分析单元测试(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 153.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-21 14:45:05 | ||
图片预览




文档简介
2022年春人教版初中八年级数学下册
第二十章 数据的分析
班级:________ 姓名:________ 分数:________
一、选择题:以下每小题均有A、B、C、D四个选项,其中只有一个选项正确,每小题3分,共36分.
1. 为增强学生的环保意识,共建绿色文明校园,某学校组织“废纸宝宝旅行记”活动.经统计,七年级5个班级一周回收废纸情况为:一班4.5 kg,二班4.4 kg,三班5.1 kg,四班3.3 kg,五班5.7 kg,则每个班级回收废纸的平均重量为( )
A.5 kg B.4.8 kg C.4.6 kg D.4.5 kg
2. 某校为加强学生出行的安全意识,学校每月都要对学生进行安全知识测评,随机选取15名学生在五月份的测评成绩如表:
成绩(分) 90 91 95 96 97 99
人数(人) 2 3 2 4 3 1
则这组数据的中位数和众数分别为( )
A.95,95 B.95,96 C.96,96 D.96,97
3. 八年级二班在一次体重测量中,小明体重54.5 kg,低于全班半数学生的体重,分析得到结论所用的统计量是( )
A.中位数 B.众数 C.平均数 D.方差
4. 现有一列数:6,3,3,4,5,4,3,增加一个数x后,这列数的中位数仍不变,则x可能是( )
A.1 B.2 C.3 D.4
5. 若一组数据:1,5,7,x的众数为5,则这组数据的平均数是( )
A.6 B.5 C.4.5 D.3.5
6. 甲、乙、丙、丁四人10次随堂测验的成绩如图所示,从图中可以看出这10次测验平均成绩较高且较稳定的是( )
A.甲 B.乙 C.丙 D.丁
7. 一家公司招考某工作岗位,只考数学和物理,计算综合得分时,按数学占60%,物理占40%计算,如果小明数学得分为80分,估计综合得分最少要达到84分才有希望,那么他的物理最少要考( )
A.86分 B.88分 C.90分 D.92分
8. 已知数据x1,x2,x3,x4,x5的平均数为k1;数据x6,x7,x8,x9,x10的平均数为k2;k1与k2的平均数是k;数据x1,x2,x3,…,x8,x9,x10的平均数为m,那么k与m的关系是( )
A.k>m B.k=m C.k<m D.不能确定
9. 小明在计算一组数据的方差时,列出的算式如下:s2=[(7-x)2+(8-x)2+(8-x)2+(8-x)2+(9-x)2],根据算式信息,下列说法中错误的是( )
A.数据个数是5 B.数据平均数是8
C.数据众数是8 D.数据的方差是0
10.已知一组数据:2,5,x,7,9的平均数是6,则这组数据的众数是( )
A.9 B.7 C.5 D.2
11.某楼四个绿化小组一天植树的棵数如下:10,x,10,8,已知这组数据唯一的众数与平均数相等,则这组数据的中位数是( )
A.8 B.9 C.10 D.12
12. 近些年来,移动支付已成为人们的主要支付方式之一.某企业为了解员工某月A,B两种移动支付方式的使用情况,从企业2 000名员工中随机抽取了200人,发现样本中A,B两种支付方式都不使用的有10人,样本中仅使用A种支付方式和仅使用B种支付方式的员工支付金额a(元)分布情况如表:
支付金额a(元) 0<a≤1 000 1 000<a≤2 000 a>2 000
仅使用A 36人 18人 6人
仅使用B 20人 28人 2人
下面有四个推断:①根据样本数据估计,企业2 000名员工中,同时使用A,B两种支付方式的为800人;②本次调查抽取的样本容量为200人;③样本中仅使用A种支付方式的员工,该月支付金额的中位数一定不超过1 000元;④样本中仅使用B种支付方式的员工,该月支付金额的众数一定为1 500元.其中正确的是( )
A.①③ B.③④ C.①② D.②④
二、填空题:每小题4分,共16分.
13.某8种食品所含的热量值分别为120,134,120,119,126,120,118,124,则这组数据的众数为__ _.
14. 某公司招聘员工,对应聘者进行三项素质测试:创新能力、综合知识、语言表达,某应聘者三项得分分别为70分,80分,90分,如果将这三项成绩按照5∶3∶2计入总成绩,则他的总成绩为__ __分.
15. 小孔同学根据朗诵比赛中9位评委给出的分数,制作了一张表格(如图表所示).如果去掉一个最高分和一个最低分,则表中数据一定不发生变化的是__ __.
平均数 中位数 众数 方差
82 83 84 0.35
16. 七名学生投篮球,每人投了10个球后,统计他们每人投中球的个数,得到七个数据,并对数据进行整理和分析,得出如图表所示信息,已知小宇投中了4个,下列判断:
平均数 中位数 众数 最小值
m 6 7 2
①可能有学生投中了9个;②投中6个的学生只有1人;③这七个数据之和可能为42;④m的值可能为5.
其中正确推断的序号是__ __.
三、解答题:本大题9小题,共98分.解答应写出必要的文字说明、证明过程或演算步骤.
17.(本题满分12分) 某工厂有220名员工,财务科要了解员工收入情况.现在抽测了10名员工的本月收入,结果如下:(单位:元)4 660,4 540,4 510,4 670,4 620,4 580,4 580,4 600,4 620,4 620.
(1)全厂员工的月平均收入是__ __元;
(2)平均每名员工的年薪是__ __元;
(3)财务科本月应准备多少钱发工资?
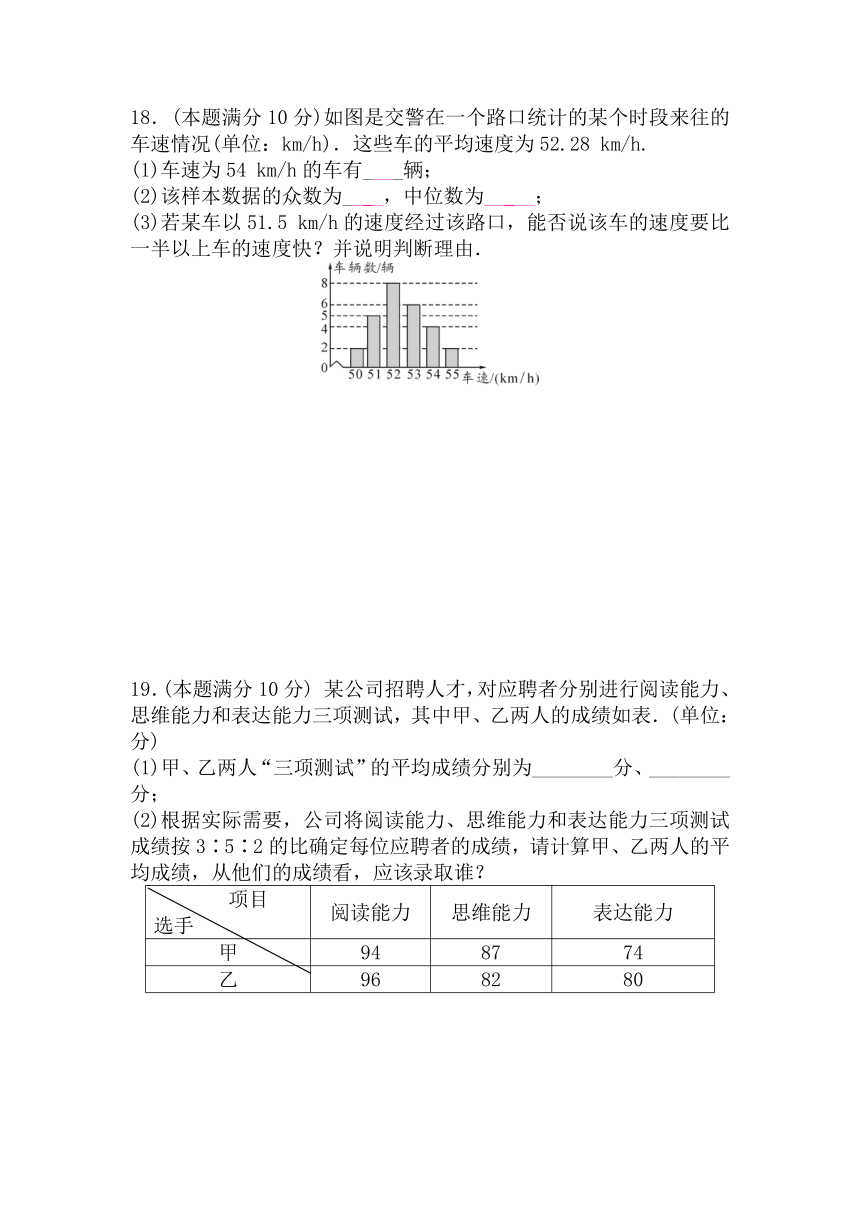
18.(本题满分10分)如图是交警在一个路口统计的某个时段来往的车速情况(单位:km/h).这些车的平均速度为52.28 km/h.
(1)车速为54 km/h的车有____辆;
(2)该样本数据的众数为__ _,中位数为__ __;
(3)若某车以51.5 km/h的速度经过该路口,能否说该车的速度要比一半以上车的速度快?并说明判断理由.
19.(本题满分10分) 某公司招聘人才,对应聘者分别进行阅读能力、思维能力和表达能力三项测试,其中甲、乙两人的成绩如表.(单位:分)
(1)甲、乙两人“三项测试”的平均成绩分别为________分、________分;
(2)根据实际需要,公司将阅读能力、思维能力和表达能力三项测试成绩按3∶5∶2的比确定每位应聘者的成绩,请计算甲、乙两人的平均成绩,从他们的成绩看,应该录取谁?
项目 选手 阅读能力 思维能力 表达能力
甲 94 87 74
乙 96 82 80
20.(本题满分10分)有甲、乙两种新品种的水稻,在进行杂交配系时要选取产量高、稳定性较好的一种,种植后各抽取5块田获取数据,每亩产量分别如表:(单位:kg)
(1)哪一品种平均亩产较高?
(2)哪一品种稳定性较好?
(3)据统计,应选哪一品种做杂交配系?
1 2 3 4 5
甲 52 50 51 49 53
乙 51 51 51 48 54
21.(本题满分10分)在某旅游景区上山的一条小路上,有一些断断续续的台阶,如图所示是其中的甲、乙两段台阶的示意图.请用所学过的有关统计知识(平均数、中位数、方差和极差)回答下列问题:
(1)分别求出两段台阶高度的中位数;
(2)哪段台阶走起来更舒服?为什么?
22.(本题满分10分)云南特产褚橙味甜皮薄,每年上市后供不应求.某超市水果销售部有营业员15人,某月该超市这15名营业员销售褚橙的数量统计如表所示:
月销售量/件 1 770 480 220 180 120 90
人数 1 1 3 3 3 4
(1)求这15名营业员该月销售量数据的平均数、中位数及众数;
(2)为了调动大多数营业员的积极性,实行“每天定额售量,超出有奖”的措施.如果你是管理者,你选择确定“定额”的统计量为 ________(选填“中位数”或“众数”).
23.(本题满分12分) 某农业科技部门为了解甲、乙两种新品西瓜的品质(大小、甜度等),进行了抽样调查.在相同条件下,随机抽取了两种西瓜各7份样品,对西瓜的品质进行评分(百分制),并对数据进行收集、整理,下面给出两种西瓜得分的统计图表.
甲、乙两种西瓜得分表
序号 1 2 3 4 5 6 7
甲种西瓜(分) 75 85 86 88 90 96 96
乙种西瓜(分) 80 83 87 90 90 92 94
甲、乙两种西瓜得分统计表
平均数 中位数 众数
甲种西瓜 88 a 96
乙种西瓜 88 90 b
(1)a=____,b=__ __;
(2)从方差的角度看,__ __(选填“甲”或“乙”)种西瓜的得分较稳定;
(3)小明认为甲种西瓜的品质较好些,小军认为乙种西瓜的品质较好些.请结合统计图表中的信息分别写出他们的理由.
24.(本题满分12分) 某市在实施居民用水定额管理前,对居民生活用水情况进行了调查.通过简单随机抽样,获得了100个家庭去年的月均用水量数据,将这组数据按从小到大的顺序排列,其中部分数据如表:
序号 1 2 … 25 26 … 50 51 … 75 76 … 99 100
月均用水量/t 1.3 1.3 … 4.5 4.5 … 6.4 6.8 … 11 13 … 25.6 28
(1)求这组数据的中位数.已知这组数据的平均数为9.2 t,你对它与中位数的差异有什么看法?
(2)为了鼓励节约用水,要确定一个用水量的标准,超出这个标准的部分按1.5倍价格收费.若要使75%的家庭水费支出不受影响,你觉得这个标准应该定为多少?
25.(本题满分12分) 八一中学为普及抗疫防疫知识,在七、八年级举行了一次防疫知识竞赛,为了解这两个年级学生的竞赛成绩,分别从两个年级各随机抽取了20名学生的成绩,进行整理、描述和分析,给出了如下信息.
各年级成绩分布如表:(注:成绩在60分以下为不合格,80分及以上为优秀)
年级 0≤x≤49 50≤x≤59 60≤x≤69 70≤x≤79 80≤x≤89 90≤x≤100
七 1 4 6 2 4 3
八 4 4 3 2 5 2
其中七年级成绩在60≤x≤69一组的是62,63,65,66,68,69,七、八年级成绩的平均数、中位数、方差、合格率、优秀率等如表:
年级 平均数 中位数 方差 合格率 优秀率
七 66.8 a 83.5 75% 35%
八 64.3 63 125.6 60% b
根据以上信息,回答下列问题:
(1)表中,a=__ __,b=__ _;
(2)小明的成绩在此次抽样之中,与他所在年级的抽样相比,小明的成绩高于平均数,却排在了后十名,则小明是__ __(选填“七”或“八”)年级的学生;
(3)请推断出哪个年级的竞赛成绩更好,并说明理由(至少从三个不同的角度说明).
参考答案
一、选择题:以下每小题均有A、B、C、D四个选项,其中只有一个选项正确,每小题3分,共36分.
1. 为增强学生的环保意识,共建绿色文明校园,某学校组织“废纸宝宝旅行记”活动.经统计,七年级5个班级一周回收废纸情况为:一班4.5 kg,二班4.4 kg,三班5.1 kg,四班3.3 kg,五班5.7 kg,则每个班级回收废纸的平均重量为( C )
A.5 kg B.4.8 kg C.4.6 kg D.4.5 kg
2. 某校为加强学生出行的安全意识,学校每月都要对学生进行安全知识测评,随机选取15名学生在五月份的测评成绩如表:
成绩(分) 90 91 95 96 97 99
人数(人) 2 3 2 4 3 1
则这组数据的中位数和众数分别为( C )
A.95,95 B.95,96 C.96,96 D.96,97
3. 八年级二班在一次体重测量中,小明体重54.5 kg,低于全班半数学生的体重,分析得到结论所用的统计量是( A )
A.中位数 B.众数 C.平均数 D.方差
4. 现有一列数:6,3,3,4,5,4,3,增加一个数x后,这列数的中位数仍不变,则x可能是( D )
A.1 B.2 C.3 D.4
5. 若一组数据:1,5,7,x的众数为5,则这组数据的平均数是( C )
A.6 B.5 C.4.5 D.3.5
6. 甲、乙、丙、丁四人10次随堂测验的成绩如图所示,从图中可以看出这10次测验平均成绩较高且较稳定的是( C )
A.甲 B.乙 C.丙 D.丁
7. 一家公司招考某工作岗位,只考数学和物理,计算综合得分时,按数学占60%,物理占40%计算,如果小明数学得分为80分,估计综合得分最少要达到84分才有希望,那么他的物理最少要考( C )
A.86分 B.88分 C.90分 D.92分
8. 已知数据x1,x2,x3,x4,x5的平均数为k1;数据x6,x7,x8,x9,x10的平均数为k2;k1与k2的平均数是k;数据x1,x2,x3,…,x8,x9,x10的平均数为m,那么k与m的关系是( B )
A.k>m B.k=m C.k<m D.不能确定
9. 小明在计算一组数据的方差时,列出的算式如下:s2=[(7-x)2+(8-x)2+(8-x)2+(8-x)2+(9-x)2],根据算式信息,下列说法中错误的是( D )
A.数据个数是5 B.数据平均数是8
C.数据众数是8 D.数据的方差是0
10.已知一组数据:2,5,x,7,9的平均数是6,则这组数据的众数是( B )
A.9 B.7 C.5 D.2
11.某楼四个绿化小组一天植树的棵数如下:10,x,10,8,已知这组数据唯一的众数与平均数相等,则这组数据的中位数是( C )
A.8 B.9 C.10 D.12
12. 近些年来,移动支付已成为人们的主要支付方式之一.某企业为了解员工某月A,B两种移动支付方式的使用情况,从企业2 000名员工中随机抽取了200人,发现样本中A,B两种支付方式都不使用的有10人,样本中仅使用A种支付方式和仅使用B种支付方式的员工支付金额a(元)分布情况如表:
支付金额a(元) 0<a≤1 000 1 000<a≤2 000 a>2 000
仅使用A 36人 18人 6人
仅使用B 20人 28人 2人
下面有四个推断:①根据样本数据估计,企业2 000名员工中,同时使用A,B两种支付方式的为800人;②本次调查抽取的样本容量为200人;③样本中仅使用A种支付方式的员工,该月支付金额的中位数一定不超过1 000元;④样本中仅使用B种支付方式的员工,该月支付金额的众数一定为1 500元.其中正确的是( A )
A.①③ B.③④ C.①② D.②④
二、填空题:每小题4分,共16分.
13.某8种食品所含的热量值分别为120,134,120,119,126,120,118,124,则这组数据的众数为__120__.
14. 某公司招聘员工,对应聘者进行三项素质测试:创新能力、综合知识、语言表达,某应聘者三项得分分别为70分,80分,90分,如果将这三项成绩按照5∶3∶2计入总成绩,则他的总成绩为__77__分.
15. 小孔同学根据朗诵比赛中9位评委给出的分数,制作了一张表格(如图表所示).如果去掉一个最高分和一个最低分,则表中数据一定不发生变化的是__中位数__.
平均数 中位数 众数 方差
82 83 84 0.35
16. 七名学生投篮球,每人投了10个球后,统计他们每人投中球的个数,得到七个数据,并对数据进行整理和分析,得出如图表所示信息,已知小宇投中了4个,下列判断:
平均数 中位数 众数 最小值
m 6 7 2
①可能有学生投中了9个;②投中6个的学生只有1人;③这七个数据之和可能为42;④m的值可能为5.
其中正确推断的序号是__①④__.
三、解答题:本大题9小题,共98分.解答应写出必要的文字说明、证明过程或演算步骤.
17.(本题满分12分) 某工厂有220名员工,财务科要了解员工收入情况.现在抽测了10名员工的本月收入,结果如下:(单位:元)4 660,4 540,4 510,4 670,4 620,4 580,4 580,4 600,4 620,4 620.
(1)全厂员工的月平均收入是__4_600__元;
(2)平均每名员工的年薪是__55_200__元;
(3)财务科本月应准备多少钱发工资?
解:(3)从(1)得到员工的月平均收入为4 600元,工厂共有220名员工,
∴财务科本月应准备4 600×220=101.2(万元).
18.(本题满分10分)如图是交警在一个路口统计的某个时段来往的车速情况(单位:km/h).这些车的平均速度为52.28 km/h.
(1)车速为54 km/h的车有__4__辆;
(2)该样本数据的众数为__52_km/h__,中位数为__52_km/h__;
(3)若某车以51.5 km/h的速度经过该路口,能否说该车的速度要比一半以上车的速度快?并说明判断理由.
解:(3)不能.
理由:因为由(2)知样本的中位数为52,所以可以估计该路段的车辆大约有一半的车速要快于52 km/h,该车的速度是51.5 km/h,小于52 km/h,所以不能说该车的速度要比一半以上车的速度快.
19.(本题满分10分) 某公司招聘人才,对应聘者分别进行阅读能力、思维能力和表达能力三项测试,其中甲、乙两人的成绩如表.(单位:分)
(1)甲、乙两人“三项测试”的平均成绩分别为________分、________分;
(2)根据实际需要,公司将阅读能力、思维能力和表达能力三项测试成绩按3∶5∶2的比确定每位应聘者的成绩,请计算甲、乙两人的平均成绩,从他们的成绩看,应该录取谁?
项目 选手 阅读能力 思维能力 表达能力
甲 94 87 74
乙 96 82 80
解:(1)85;86.
(2)甲的平均成绩为86.5分,
乙的平均成绩为85.8分,
∴应该录取甲.
20.(本题满分10分)有甲、乙两种新品种的水稻,在进行杂交配系时要选取产量高、稳定性较好的一种,种植后各抽取5块田获取数据,每亩产量分别如表:(单位:kg)
(1)哪一品种平均亩产较高?
(2)哪一品种稳定性较好?
(3)据统计,应选哪一品种做杂交配系?
1 2 3 4 5
甲 52 50 51 49 53
乙 51 51 51 48 54
解:(1)x甲=51 kg,x乙=51 kg,∴甲、乙平均亩产相同.
(2)s=2 kg2,s=3.6 kg2,∵s(3)应选择甲品种做杂交配系.
21.(本题满分10分)在某旅游景区上山的一条小路上,有一些断断续续的台阶,如图所示是其中的甲、乙两段台阶的示意图.请用所学过的有关统计知识(平均数、中位数、方差和极差)回答下列问题:
(1)分别求出两段台阶高度的中位数;
(2)哪段台阶走起来更舒服?为什么?
解:(1)将甲路段台阶高度重新排列为14,14,15,15,16,16,
乙路段台阶高度重新排列为10,11,15,17,18,19,
所以甲路段高度的中位数为=15,
乙路段高度的中位数为=16.
(2)甲路段台阶走起来更舒服一些,理由:由题意知,甲路段台阶的高度波动小于乙路段台阶高度波动,即甲路段的台阶高度方差小.
22.(本题满分10分)云南特产褚橙味甜皮薄,每年上市后供不应求.某超市水果销售部有营业员15人,某月该超市这15名营业员销售褚橙的数量统计如表所示:
月销售量/件 1 770 480 220 180 120 90
人数 1 1 3 3 3 4
(1)求这15名营业员该月销售量数据的平均数、中位数及众数;
(2)为了调动大多数营业员的积极性,实行“每天定额售量,超出有奖”的措施.如果你是管理者,你选择确定“定额”的统计量为 ________(选填“中位数”或“众数”).
解:(1)这15名营业员该月销售量数据的平均数、中位数及众数分别为278件,180件,90件.
(2)中位数.
23.(本题满分12分) 某农业科技部门为了解甲、乙两种新品西瓜的品质(大小、甜度等),进行了抽样调查.在相同条件下,随机抽取了两种西瓜各7份样品,对西瓜的品质进行评分(百分制),并对数据进行收集、整理,下面给出两种西瓜得分的统计图表.
甲、乙两种西瓜得分表
序号 1 2 3 4 5 6 7
甲种西瓜(分) 75 85 86 88 90 96 96
乙种西瓜(分) 80 83 87 90 90 92 94
甲、乙两种西瓜得分统计表
平均数 中位数 众数
甲种西瓜 88 a 96
乙种西瓜 88 90 b
(1)a=__88__,b=__90__;
(2)从方差的角度看,__乙__(选填“甲”或“乙”)种西瓜的得分较稳定;
(3)小明认为甲种西瓜的品质较好些,小军认为乙种西瓜的品质较好些.请结合统计图表中的信息分别写出他们的理由.
解:(3)小明的理由为:甲种西瓜得分的众数比乙种的高.
小军的理由为:乙种西瓜得分的中位数比甲种的高.
24.(本题满分12分) 某市在实施居民用水定额管理前,对居民生活用水情况进行了调查.通过简单随机抽样,获得了100个家庭去年的月均用水量数据,将这组数据按从小到大的顺序排列,其中部分数据如表:
序号 1 2 … 25 26 … 50 51 … 75 76 … 99 100
月均用水量/t 1.3 1.3 … 4.5 4.5 … 6.4 6.8 … 11 13 … 25.6 28
(1)求这组数据的中位数.已知这组数据的平均数为9.2 t,你对它与中位数的差异有什么看法?
(2)为了鼓励节约用水,要确定一个用水量的标准,超出这个标准的部分按1.5倍价格收费.若要使75%的家庭水费支出不受影响,你觉得这个标准应该定为多少?
解:(1)中位数为(6.4+6.8)÷2=6.6;从平均数与中位数的差异可得大部分居民家庭去年的月均用水量小于平均数,有节约用水观念,少数家庭用水比较浪费.
(2)∵100×75%=75,第75个家庭去年的月均用水量为11 t,所以为了鼓励节约用水,要使75%的家庭水费支出不受影响,即要使75户的家庭水费支出不受影响,故家庭月均用水量应该定为11 t.
25.(本题满分12分) 八一中学为普及抗疫防疫知识,在七、八年级举行了一次防疫知识竞赛,为了解这两个年级学生的竞赛成绩,分别从两个年级各随机抽取了20名学生的成绩,进行整理、描述和分析,给出了如下信息.
各年级成绩分布如表:(注:成绩在60分以下为不合格,80分及以上为优秀)
年级 0≤x≤49 50≤x≤59 60≤x≤69 70≤x≤79 80≤x≤89 90≤x≤100
七 1 4 6 2 4 3
八 4 4 3 2 5 2
其中七年级成绩在60≤x≤69一组的是62,63,65,66,68,69,七、八年级成绩的平均数、中位数、方差、合格率、优秀率等如表:
年级 平均数 中位数 方差 合格率 优秀率
七 66.8 a 83.5 75% 35%
八 64.3 63 125.6 60% b
根据以上信息,回答下列问题:
(1)表中,a=__68.5__,b=__35%__;
(2)小明的成绩在此次抽样之中,与他所在年级的抽样相比,小明的成绩高于平均数,却排在了后十名,则小明是__七__(选填“七”或“八”)年级的学生;
(3)请推断出哪个年级的竞赛成绩更好,并说明理由(至少从三个不同的角度说明).
解:(3)七年级学生成绩较好,从平均数、中位数和合格率上看,七年级均较高,且七年级的竞赛成绩较稳定,因此七年级的竞赛成绩更好.
第二十章 数据的分析
班级:________ 姓名:________ 分数:________
一、选择题:以下每小题均有A、B、C、D四个选项,其中只有一个选项正确,每小题3分,共36分.
1. 为增强学生的环保意识,共建绿色文明校园,某学校组织“废纸宝宝旅行记”活动.经统计,七年级5个班级一周回收废纸情况为:一班4.5 kg,二班4.4 kg,三班5.1 kg,四班3.3 kg,五班5.7 kg,则每个班级回收废纸的平均重量为( )
A.5 kg B.4.8 kg C.4.6 kg D.4.5 kg
2. 某校为加强学生出行的安全意识,学校每月都要对学生进行安全知识测评,随机选取15名学生在五月份的测评成绩如表:
成绩(分) 90 91 95 96 97 99
人数(人) 2 3 2 4 3 1
则这组数据的中位数和众数分别为( )
A.95,95 B.95,96 C.96,96 D.96,97
3. 八年级二班在一次体重测量中,小明体重54.5 kg,低于全班半数学生的体重,分析得到结论所用的统计量是( )
A.中位数 B.众数 C.平均数 D.方差
4. 现有一列数:6,3,3,4,5,4,3,增加一个数x后,这列数的中位数仍不变,则x可能是( )
A.1 B.2 C.3 D.4
5. 若一组数据:1,5,7,x的众数为5,则这组数据的平均数是( )
A.6 B.5 C.4.5 D.3.5
6. 甲、乙、丙、丁四人10次随堂测验的成绩如图所示,从图中可以看出这10次测验平均成绩较高且较稳定的是( )
A.甲 B.乙 C.丙 D.丁
7. 一家公司招考某工作岗位,只考数学和物理,计算综合得分时,按数学占60%,物理占40%计算,如果小明数学得分为80分,估计综合得分最少要达到84分才有希望,那么他的物理最少要考( )
A.86分 B.88分 C.90分 D.92分
8. 已知数据x1,x2,x3,x4,x5的平均数为k1;数据x6,x7,x8,x9,x10的平均数为k2;k1与k2的平均数是k;数据x1,x2,x3,…,x8,x9,x10的平均数为m,那么k与m的关系是( )
A.k>m B.k=m C.k<m D.不能确定
9. 小明在计算一组数据的方差时,列出的算式如下:s2=[(7-x)2+(8-x)2+(8-x)2+(8-x)2+(9-x)2],根据算式信息,下列说法中错误的是( )
A.数据个数是5 B.数据平均数是8
C.数据众数是8 D.数据的方差是0
10.已知一组数据:2,5,x,7,9的平均数是6,则这组数据的众数是( )
A.9 B.7 C.5 D.2
11.某楼四个绿化小组一天植树的棵数如下:10,x,10,8,已知这组数据唯一的众数与平均数相等,则这组数据的中位数是( )
A.8 B.9 C.10 D.12
12. 近些年来,移动支付已成为人们的主要支付方式之一.某企业为了解员工某月A,B两种移动支付方式的使用情况,从企业2 000名员工中随机抽取了200人,发现样本中A,B两种支付方式都不使用的有10人,样本中仅使用A种支付方式和仅使用B种支付方式的员工支付金额a(元)分布情况如表:
支付金额a(元) 0<a≤1 000 1 000<a≤2 000 a>2 000
仅使用A 36人 18人 6人
仅使用B 20人 28人 2人
下面有四个推断:①根据样本数据估计,企业2 000名员工中,同时使用A,B两种支付方式的为800人;②本次调查抽取的样本容量为200人;③样本中仅使用A种支付方式的员工,该月支付金额的中位数一定不超过1 000元;④样本中仅使用B种支付方式的员工,该月支付金额的众数一定为1 500元.其中正确的是( )
A.①③ B.③④ C.①② D.②④
二、填空题:每小题4分,共16分.
13.某8种食品所含的热量值分别为120,134,120,119,126,120,118,124,则这组数据的众数为__ _.
14. 某公司招聘员工,对应聘者进行三项素质测试:创新能力、综合知识、语言表达,某应聘者三项得分分别为70分,80分,90分,如果将这三项成绩按照5∶3∶2计入总成绩,则他的总成绩为__ __分.
15. 小孔同学根据朗诵比赛中9位评委给出的分数,制作了一张表格(如图表所示).如果去掉一个最高分和一个最低分,则表中数据一定不发生变化的是__ __.
平均数 中位数 众数 方差
82 83 84 0.35
16. 七名学生投篮球,每人投了10个球后,统计他们每人投中球的个数,得到七个数据,并对数据进行整理和分析,得出如图表所示信息,已知小宇投中了4个,下列判断:
平均数 中位数 众数 最小值
m 6 7 2
①可能有学生投中了9个;②投中6个的学生只有1人;③这七个数据之和可能为42;④m的值可能为5.
其中正确推断的序号是__ __.
三、解答题:本大题9小题,共98分.解答应写出必要的文字说明、证明过程或演算步骤.
17.(本题满分12分) 某工厂有220名员工,财务科要了解员工收入情况.现在抽测了10名员工的本月收入,结果如下:(单位:元)4 660,4 540,4 510,4 670,4 620,4 580,4 580,4 600,4 620,4 620.
(1)全厂员工的月平均收入是__ __元;
(2)平均每名员工的年薪是__ __元;
(3)财务科本月应准备多少钱发工资?
18.(本题满分10分)如图是交警在一个路口统计的某个时段来往的车速情况(单位:km/h).这些车的平均速度为52.28 km/h.
(1)车速为54 km/h的车有____辆;
(2)该样本数据的众数为__ _,中位数为__ __;
(3)若某车以51.5 km/h的速度经过该路口,能否说该车的速度要比一半以上车的速度快?并说明判断理由.
19.(本题满分10分) 某公司招聘人才,对应聘者分别进行阅读能力、思维能力和表达能力三项测试,其中甲、乙两人的成绩如表.(单位:分)
(1)甲、乙两人“三项测试”的平均成绩分别为________分、________分;
(2)根据实际需要,公司将阅读能力、思维能力和表达能力三项测试成绩按3∶5∶2的比确定每位应聘者的成绩,请计算甲、乙两人的平均成绩,从他们的成绩看,应该录取谁?
项目 选手 阅读能力 思维能力 表达能力
甲 94 87 74
乙 96 82 80
20.(本题满分10分)有甲、乙两种新品种的水稻,在进行杂交配系时要选取产量高、稳定性较好的一种,种植后各抽取5块田获取数据,每亩产量分别如表:(单位:kg)
(1)哪一品种平均亩产较高?
(2)哪一品种稳定性较好?
(3)据统计,应选哪一品种做杂交配系?
1 2 3 4 5
甲 52 50 51 49 53
乙 51 51 51 48 54
21.(本题满分10分)在某旅游景区上山的一条小路上,有一些断断续续的台阶,如图所示是其中的甲、乙两段台阶的示意图.请用所学过的有关统计知识(平均数、中位数、方差和极差)回答下列问题:
(1)分别求出两段台阶高度的中位数;
(2)哪段台阶走起来更舒服?为什么?
22.(本题满分10分)云南特产褚橙味甜皮薄,每年上市后供不应求.某超市水果销售部有营业员15人,某月该超市这15名营业员销售褚橙的数量统计如表所示:
月销售量/件 1 770 480 220 180 120 90
人数 1 1 3 3 3 4
(1)求这15名营业员该月销售量数据的平均数、中位数及众数;
(2)为了调动大多数营业员的积极性,实行“每天定额售量,超出有奖”的措施.如果你是管理者,你选择确定“定额”的统计量为 ________(选填“中位数”或“众数”).
23.(本题满分12分) 某农业科技部门为了解甲、乙两种新品西瓜的品质(大小、甜度等),进行了抽样调查.在相同条件下,随机抽取了两种西瓜各7份样品,对西瓜的品质进行评分(百分制),并对数据进行收集、整理,下面给出两种西瓜得分的统计图表.
甲、乙两种西瓜得分表
序号 1 2 3 4 5 6 7
甲种西瓜(分) 75 85 86 88 90 96 96
乙种西瓜(分) 80 83 87 90 90 92 94
甲、乙两种西瓜得分统计表
平均数 中位数 众数
甲种西瓜 88 a 96
乙种西瓜 88 90 b
(1)a=____,b=__ __;
(2)从方差的角度看,__ __(选填“甲”或“乙”)种西瓜的得分较稳定;
(3)小明认为甲种西瓜的品质较好些,小军认为乙种西瓜的品质较好些.请结合统计图表中的信息分别写出他们的理由.
24.(本题满分12分) 某市在实施居民用水定额管理前,对居民生活用水情况进行了调查.通过简单随机抽样,获得了100个家庭去年的月均用水量数据,将这组数据按从小到大的顺序排列,其中部分数据如表:
序号 1 2 … 25 26 … 50 51 … 75 76 … 99 100
月均用水量/t 1.3 1.3 … 4.5 4.5 … 6.4 6.8 … 11 13 … 25.6 28
(1)求这组数据的中位数.已知这组数据的平均数为9.2 t,你对它与中位数的差异有什么看法?
(2)为了鼓励节约用水,要确定一个用水量的标准,超出这个标准的部分按1.5倍价格收费.若要使75%的家庭水费支出不受影响,你觉得这个标准应该定为多少?
25.(本题满分12分) 八一中学为普及抗疫防疫知识,在七、八年级举行了一次防疫知识竞赛,为了解这两个年级学生的竞赛成绩,分别从两个年级各随机抽取了20名学生的成绩,进行整理、描述和分析,给出了如下信息.
各年级成绩分布如表:(注:成绩在60分以下为不合格,80分及以上为优秀)
年级 0≤x≤49 50≤x≤59 60≤x≤69 70≤x≤79 80≤x≤89 90≤x≤100
七 1 4 6 2 4 3
八 4 4 3 2 5 2
其中七年级成绩在60≤x≤69一组的是62,63,65,66,68,69,七、八年级成绩的平均数、中位数、方差、合格率、优秀率等如表:
年级 平均数 中位数 方差 合格率 优秀率
七 66.8 a 83.5 75% 35%
八 64.3 63 125.6 60% b
根据以上信息,回答下列问题:
(1)表中,a=__ __,b=__ _;
(2)小明的成绩在此次抽样之中,与他所在年级的抽样相比,小明的成绩高于平均数,却排在了后十名,则小明是__ __(选填“七”或“八”)年级的学生;
(3)请推断出哪个年级的竞赛成绩更好,并说明理由(至少从三个不同的角度说明).
参考答案
一、选择题:以下每小题均有A、B、C、D四个选项,其中只有一个选项正确,每小题3分,共36分.
1. 为增强学生的环保意识,共建绿色文明校园,某学校组织“废纸宝宝旅行记”活动.经统计,七年级5个班级一周回收废纸情况为:一班4.5 kg,二班4.4 kg,三班5.1 kg,四班3.3 kg,五班5.7 kg,则每个班级回收废纸的平均重量为( C )
A.5 kg B.4.8 kg C.4.6 kg D.4.5 kg
2. 某校为加强学生出行的安全意识,学校每月都要对学生进行安全知识测评,随机选取15名学生在五月份的测评成绩如表:
成绩(分) 90 91 95 96 97 99
人数(人) 2 3 2 4 3 1
则这组数据的中位数和众数分别为( C )
A.95,95 B.95,96 C.96,96 D.96,97
3. 八年级二班在一次体重测量中,小明体重54.5 kg,低于全班半数学生的体重,分析得到结论所用的统计量是( A )
A.中位数 B.众数 C.平均数 D.方差
4. 现有一列数:6,3,3,4,5,4,3,增加一个数x后,这列数的中位数仍不变,则x可能是( D )
A.1 B.2 C.3 D.4
5. 若一组数据:1,5,7,x的众数为5,则这组数据的平均数是( C )
A.6 B.5 C.4.5 D.3.5
6. 甲、乙、丙、丁四人10次随堂测验的成绩如图所示,从图中可以看出这10次测验平均成绩较高且较稳定的是( C )
A.甲 B.乙 C.丙 D.丁
7. 一家公司招考某工作岗位,只考数学和物理,计算综合得分时,按数学占60%,物理占40%计算,如果小明数学得分为80分,估计综合得分最少要达到84分才有希望,那么他的物理最少要考( C )
A.86分 B.88分 C.90分 D.92分
8. 已知数据x1,x2,x3,x4,x5的平均数为k1;数据x6,x7,x8,x9,x10的平均数为k2;k1与k2的平均数是k;数据x1,x2,x3,…,x8,x9,x10的平均数为m,那么k与m的关系是( B )
A.k>m B.k=m C.k<m D.不能确定
9. 小明在计算一组数据的方差时,列出的算式如下:s2=[(7-x)2+(8-x)2+(8-x)2+(8-x)2+(9-x)2],根据算式信息,下列说法中错误的是( D )
A.数据个数是5 B.数据平均数是8
C.数据众数是8 D.数据的方差是0
10.已知一组数据:2,5,x,7,9的平均数是6,则这组数据的众数是( B )
A.9 B.7 C.5 D.2
11.某楼四个绿化小组一天植树的棵数如下:10,x,10,8,已知这组数据唯一的众数与平均数相等,则这组数据的中位数是( C )
A.8 B.9 C.10 D.12
12. 近些年来,移动支付已成为人们的主要支付方式之一.某企业为了解员工某月A,B两种移动支付方式的使用情况,从企业2 000名员工中随机抽取了200人,发现样本中A,B两种支付方式都不使用的有10人,样本中仅使用A种支付方式和仅使用B种支付方式的员工支付金额a(元)分布情况如表:
支付金额a(元) 0<a≤1 000 1 000<a≤2 000 a>2 000
仅使用A 36人 18人 6人
仅使用B 20人 28人 2人
下面有四个推断:①根据样本数据估计,企业2 000名员工中,同时使用A,B两种支付方式的为800人;②本次调查抽取的样本容量为200人;③样本中仅使用A种支付方式的员工,该月支付金额的中位数一定不超过1 000元;④样本中仅使用B种支付方式的员工,该月支付金额的众数一定为1 500元.其中正确的是( A )
A.①③ B.③④ C.①② D.②④
二、填空题:每小题4分,共16分.
13.某8种食品所含的热量值分别为120,134,120,119,126,120,118,124,则这组数据的众数为__120__.
14. 某公司招聘员工,对应聘者进行三项素质测试:创新能力、综合知识、语言表达,某应聘者三项得分分别为70分,80分,90分,如果将这三项成绩按照5∶3∶2计入总成绩,则他的总成绩为__77__分.
15. 小孔同学根据朗诵比赛中9位评委给出的分数,制作了一张表格(如图表所示).如果去掉一个最高分和一个最低分,则表中数据一定不发生变化的是__中位数__.
平均数 中位数 众数 方差
82 83 84 0.35
16. 七名学生投篮球,每人投了10个球后,统计他们每人投中球的个数,得到七个数据,并对数据进行整理和分析,得出如图表所示信息,已知小宇投中了4个,下列判断:
平均数 中位数 众数 最小值
m 6 7 2
①可能有学生投中了9个;②投中6个的学生只有1人;③这七个数据之和可能为42;④m的值可能为5.
其中正确推断的序号是__①④__.
三、解答题:本大题9小题,共98分.解答应写出必要的文字说明、证明过程或演算步骤.
17.(本题满分12分) 某工厂有220名员工,财务科要了解员工收入情况.现在抽测了10名员工的本月收入,结果如下:(单位:元)4 660,4 540,4 510,4 670,4 620,4 580,4 580,4 600,4 620,4 620.
(1)全厂员工的月平均收入是__4_600__元;
(2)平均每名员工的年薪是__55_200__元;
(3)财务科本月应准备多少钱发工资?
解:(3)从(1)得到员工的月平均收入为4 600元,工厂共有220名员工,
∴财务科本月应准备4 600×220=101.2(万元).
18.(本题满分10分)如图是交警在一个路口统计的某个时段来往的车速情况(单位:km/h).这些车的平均速度为52.28 km/h.
(1)车速为54 km/h的车有__4__辆;
(2)该样本数据的众数为__52_km/h__,中位数为__52_km/h__;
(3)若某车以51.5 km/h的速度经过该路口,能否说该车的速度要比一半以上车的速度快?并说明判断理由.
解:(3)不能.
理由:因为由(2)知样本的中位数为52,所以可以估计该路段的车辆大约有一半的车速要快于52 km/h,该车的速度是51.5 km/h,小于52 km/h,所以不能说该车的速度要比一半以上车的速度快.
19.(本题满分10分) 某公司招聘人才,对应聘者分别进行阅读能力、思维能力和表达能力三项测试,其中甲、乙两人的成绩如表.(单位:分)
(1)甲、乙两人“三项测试”的平均成绩分别为________分、________分;
(2)根据实际需要,公司将阅读能力、思维能力和表达能力三项测试成绩按3∶5∶2的比确定每位应聘者的成绩,请计算甲、乙两人的平均成绩,从他们的成绩看,应该录取谁?
项目 选手 阅读能力 思维能力 表达能力
甲 94 87 74
乙 96 82 80
解:(1)85;86.
(2)甲的平均成绩为86.5分,
乙的平均成绩为85.8分,
∴应该录取甲.
20.(本题满分10分)有甲、乙两种新品种的水稻,在进行杂交配系时要选取产量高、稳定性较好的一种,种植后各抽取5块田获取数据,每亩产量分别如表:(单位:kg)
(1)哪一品种平均亩产较高?
(2)哪一品种稳定性较好?
(3)据统计,应选哪一品种做杂交配系?
1 2 3 4 5
甲 52 50 51 49 53
乙 51 51 51 48 54
解:(1)x甲=51 kg,x乙=51 kg,∴甲、乙平均亩产相同.
(2)s=2 kg2,s=3.6 kg2,∵s
21.(本题满分10分)在某旅游景区上山的一条小路上,有一些断断续续的台阶,如图所示是其中的甲、乙两段台阶的示意图.请用所学过的有关统计知识(平均数、中位数、方差和极差)回答下列问题:
(1)分别求出两段台阶高度的中位数;
(2)哪段台阶走起来更舒服?为什么?
解:(1)将甲路段台阶高度重新排列为14,14,15,15,16,16,
乙路段台阶高度重新排列为10,11,15,17,18,19,
所以甲路段高度的中位数为=15,
乙路段高度的中位数为=16.
(2)甲路段台阶走起来更舒服一些,理由:由题意知,甲路段台阶的高度波动小于乙路段台阶高度波动,即甲路段的台阶高度方差小.
22.(本题满分10分)云南特产褚橙味甜皮薄,每年上市后供不应求.某超市水果销售部有营业员15人,某月该超市这15名营业员销售褚橙的数量统计如表所示:
月销售量/件 1 770 480 220 180 120 90
人数 1 1 3 3 3 4
(1)求这15名营业员该月销售量数据的平均数、中位数及众数;
(2)为了调动大多数营业员的积极性,实行“每天定额售量,超出有奖”的措施.如果你是管理者,你选择确定“定额”的统计量为 ________(选填“中位数”或“众数”).
解:(1)这15名营业员该月销售量数据的平均数、中位数及众数分别为278件,180件,90件.
(2)中位数.
23.(本题满分12分) 某农业科技部门为了解甲、乙两种新品西瓜的品质(大小、甜度等),进行了抽样调查.在相同条件下,随机抽取了两种西瓜各7份样品,对西瓜的品质进行评分(百分制),并对数据进行收集、整理,下面给出两种西瓜得分的统计图表.
甲、乙两种西瓜得分表
序号 1 2 3 4 5 6 7
甲种西瓜(分) 75 85 86 88 90 96 96
乙种西瓜(分) 80 83 87 90 90 92 94
甲、乙两种西瓜得分统计表
平均数 中位数 众数
甲种西瓜 88 a 96
乙种西瓜 88 90 b
(1)a=__88__,b=__90__;
(2)从方差的角度看,__乙__(选填“甲”或“乙”)种西瓜的得分较稳定;
(3)小明认为甲种西瓜的品质较好些,小军认为乙种西瓜的品质较好些.请结合统计图表中的信息分别写出他们的理由.
解:(3)小明的理由为:甲种西瓜得分的众数比乙种的高.
小军的理由为:乙种西瓜得分的中位数比甲种的高.
24.(本题满分12分) 某市在实施居民用水定额管理前,对居民生活用水情况进行了调查.通过简单随机抽样,获得了100个家庭去年的月均用水量数据,将这组数据按从小到大的顺序排列,其中部分数据如表:
序号 1 2 … 25 26 … 50 51 … 75 76 … 99 100
月均用水量/t 1.3 1.3 … 4.5 4.5 … 6.4 6.8 … 11 13 … 25.6 28
(1)求这组数据的中位数.已知这组数据的平均数为9.2 t,你对它与中位数的差异有什么看法?
(2)为了鼓励节约用水,要确定一个用水量的标准,超出这个标准的部分按1.5倍价格收费.若要使75%的家庭水费支出不受影响,你觉得这个标准应该定为多少?
解:(1)中位数为(6.4+6.8)÷2=6.6;从平均数与中位数的差异可得大部分居民家庭去年的月均用水量小于平均数,有节约用水观念,少数家庭用水比较浪费.
(2)∵100×75%=75,第75个家庭去年的月均用水量为11 t,所以为了鼓励节约用水,要使75%的家庭水费支出不受影响,即要使75户的家庭水费支出不受影响,故家庭月均用水量应该定为11 t.
25.(本题满分12分) 八一中学为普及抗疫防疫知识,在七、八年级举行了一次防疫知识竞赛,为了解这两个年级学生的竞赛成绩,分别从两个年级各随机抽取了20名学生的成绩,进行整理、描述和分析,给出了如下信息.
各年级成绩分布如表:(注:成绩在60分以下为不合格,80分及以上为优秀)
年级 0≤x≤49 50≤x≤59 60≤x≤69 70≤x≤79 80≤x≤89 90≤x≤100
七 1 4 6 2 4 3
八 4 4 3 2 5 2
其中七年级成绩在60≤x≤69一组的是62,63,65,66,68,69,七、八年级成绩的平均数、中位数、方差、合格率、优秀率等如表:
年级 平均数 中位数 方差 合格率 优秀率
七 66.8 a 83.5 75% 35%
八 64.3 63 125.6 60% b
根据以上信息,回答下列问题:
(1)表中,a=__68.5__,b=__35%__;
(2)小明的成绩在此次抽样之中,与他所在年级的抽样相比,小明的成绩高于平均数,却排在了后十名,则小明是__七__(选填“七”或“八”)年级的学生;
(3)请推断出哪个年级的竞赛成绩更好,并说明理由(至少从三个不同的角度说明).
解:(3)七年级学生成绩较好,从平均数、中位数和合格率上看,七年级均较高,且七年级的竞赛成绩较稳定,因此七年级的竞赛成绩更好.
