2021-2022学年人教版八年级数学下册18.2.1矩形课后练习(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版八年级数学下册18.2.1矩形课后练习(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 226.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-21 14:47:48 | ||
图片预览



文档简介
2021——2022学年度人教版八年级数学下册 第十八章 平行四边形
18.2.1矩形 课后练习
一、选择题
1.矩形具有而一般平行四边形不具有的性质是( )
A.对边平行且相等 B.对角线相等
C.对角线互相平分 D.对角线互相垂直
2.一个矩形的两条对角线的一个夹角为,对角线长为,则这个矩形较短边的长为( )
A. B. C. D.
3.如图,矩形ABCD中,对角线AC和BD交于点O,E为BC中点.若AC=8,∠ACB=30°,则OE的长为( )
A.2 B.3 C.4 D.4
4.如图,矩形中,对角线交于点O,,则矩形的面积是( )
A.2 B. C. D.8
5.如图,矩形ABCD的对角线AC与BD相交于点O,夹角∠AOB=60°,已知AB=1,则△ABD的面积是( )
A.1 B.2 C. D.
6.如图,矩形ABCD中,AB=2BC,点E在CD上,AE=AB,则∠ABE的度数为( )
A.60° B.70° C.72° D.75°
7.已知在矩形ABCD中,对角线AC、BD交于点O,,点E在边AD上,,点F在边BC上,将四边形CDEF沿EF翻折,点D恰好与点O重合,则CF的长为( )
A. B. C. D.
8.如图,在中,,,AD平分交BC于点D,点E为AC的中点,连接DE,则的周长为( )
A.12 B.13 C.14 D.18
9.如图,在中,对角线、相交于点O,且,则的度数为( )
A. B. C. D.
10.如图,AC、BC、BE、DE是四根长度均为10cm的火柴棒,点A、B、D共线.若AB=12cm,BD=16cm,点C和点E之间的距离是( )
A. B. C. D.
二、填空题
11.在矩形ABCD中对角线AC,BD交于点O,且.若,则BC长为_________.
12.在矩形中,,点E在直线上,是以为底的等腰三角形,则线段的长度为_______.
13.如图,在中,,,是的中点,若的周长等于6,则__________.
14.在矩形ABCD中,AB=2,BC=2AB,E是AB上的一点,沿CE将△EBC上翻折,若B点恰好落在边AD上的F点,则AF=______.
15.如图,在矩形ABCD中,AB=3a,BC=4a,若点E是边AD上一点,点F是矩形内一点,∠BCF=30°,则EF+CF的最小值是_____.
三、解答题
16.如图,在矩形ABCD中,,对角线AC、BD相交于点O,求的度数.
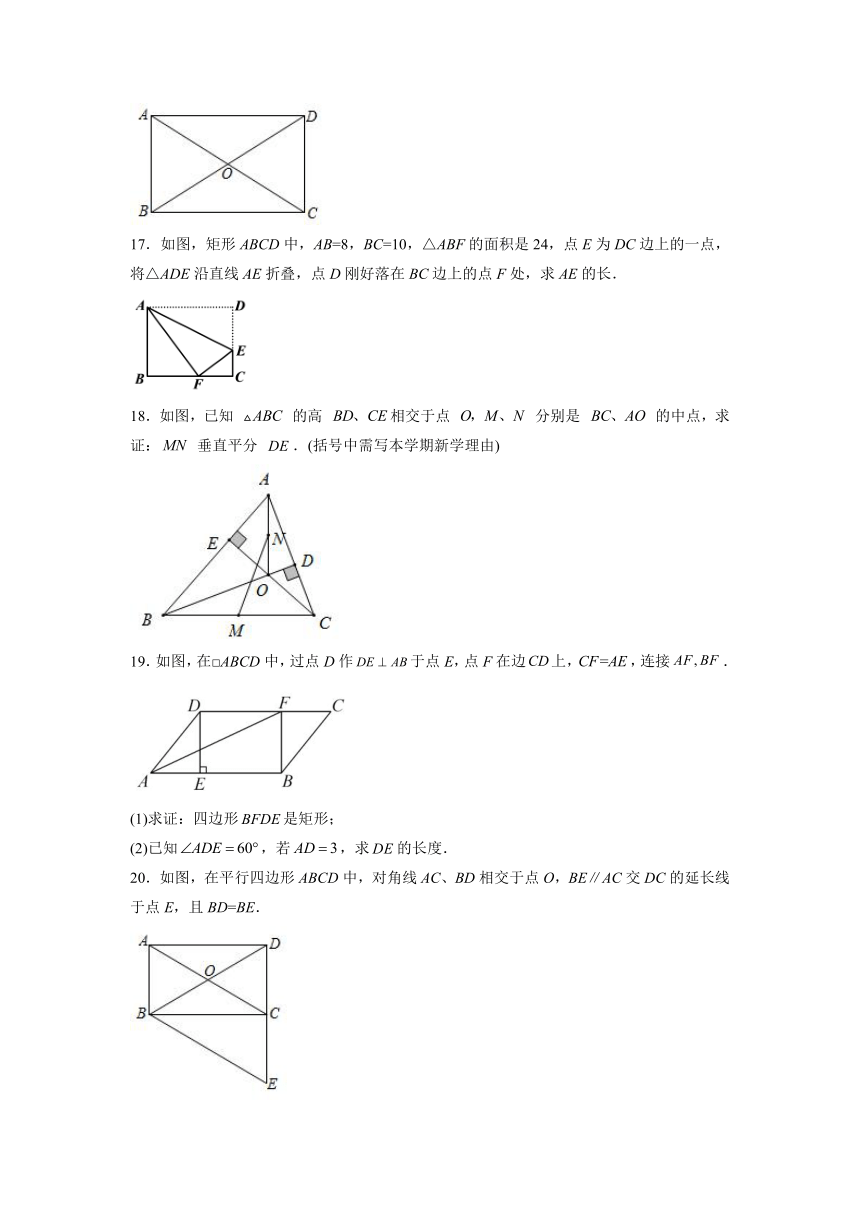
17.如图,矩形ABCD中,AB=8,BC=10,△ABF的面积是24,点E为DC边上的一点,将△ADE沿直线AE折叠,点D刚好落在BC边上的点F处,求AE的长.
18.如图,已知 的高 相交于点 分别是 的中点,求证: 垂直平分 .(括号中需写本学期新学理由)
19.如图,在□ABCD中,过点D作于点E,点F在边上,,连接.
(1)求证:四边形是矩形;
(2)已知,若,求的长度.
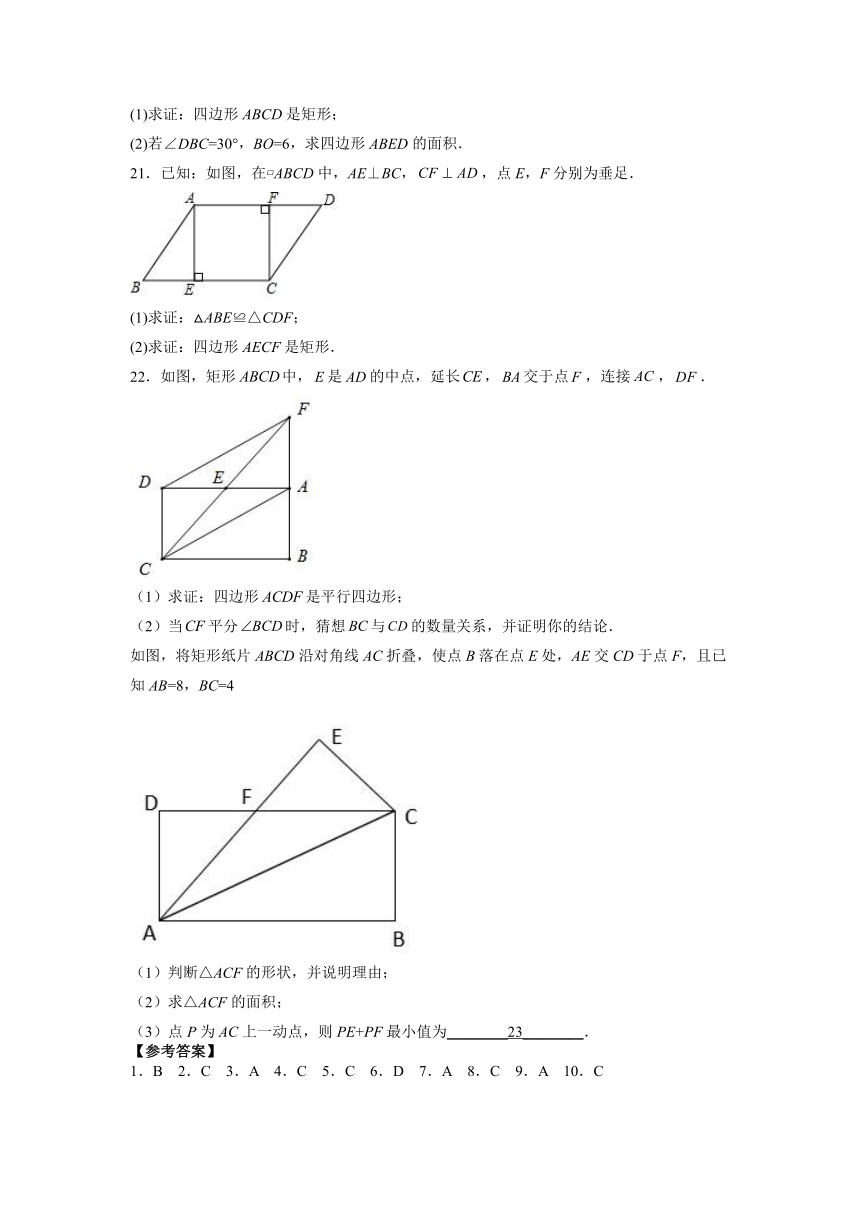
20.如图,在平行四边形ABCD中,对角线AC、BD相交于点O,BE∥AC交DC的延长线于点E,且BD=BE.
(1)求证:四边形ABCD是矩形;
(2)若∠DBC=30°,BO=6,求四边形ABED的面积.
21.已知:如图,在 ABCD中,AE⊥BC,,点E,F分别为垂足.
(1)求证:△ABE≌△CDF;
(2)求证:四边形AECF是矩形.
22.如图,矩形中,是的中点,延长,交于点,连接,.
(1)求证:四边形是平行四边形;
(2)当平分时,猜想与的数量关系,并证明你的结论.
如图,将矩形纸片ABCD沿对角线AC折叠,使点B落在点E处,AE交CD于点F,且已知AB=8,BC=4
(1)判断△ACF的形状,并说明理由;
(2)求△ACF的面积;
(3)点P为AC上一动点,则PE+PF最小值为________23________.
【参考答案】
1.B 2.C 3.A 4.C 5.C 6.D 7.A 8.C 9.A 10.C
11.
12.
13.4
14.
15.3a
16.解:∵四边形ABCD为矩形,
∴,,,
∵,
∴,
∴,
∴.
17.解:∵四边形ABCD是矩形,AB=8,BC=10,
∴AB=CD=8,BC=AD=10,∠B=∠C=∠D=90°,
∵△ABF的面积是24,
∴,
∴,
∴CF=4,
由折叠的性质可得:DE=EF,
设EF=DE=x,则CE=8-x,
在Rt△ECF中,由勾股定理可得:,
解得:,即,
在Rt△ADE中,.
18.证明:联结,
∵ , ,
∴ ,
∵ 是 的中点 ,
∴ (直角三角形斜边中线等于斜边一半),
∴ ,
∴ 在线段的垂直平分线上 (垂直平分线的逆定理) ,
∴ 垂直平分 .
19.(1)证明:∵四边形是平行四边形,
∴,DC=AB.
∵CF=AE,
∴DF=BE且DF||BE,
∴四边形是平行四边形.
又∵DE⊥AB ,∴∠DEB=90°,
∴四边形是矩形.
(2)解:∵∠ADE=60°,DE⊥AB,
∴∠DAE=30°,
又∵,
∴DE=AD=
20.(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,
又∵点E在DC的延长线上,
∴AB∥CE,
又∵BE∥AC,
∴四边形ABEC是平行四边形,
∴AC=BE,
又BD=BE,
∴AC=BD,
∴平行四边形ABCD是矩形;
(2)解:∵在矩形ABCD中,∠DBC=30°,OA=OB,
∴∠ABD=60°,
∴△AOB是等边三角形,
∴AB=BO=6,
∴BD=2BO=2×6=12,
又∵四边形ABEC是平行四边形,
∴CE=AB=6,
∴DE=CD+CE=12,
在Rt△ABC中,BC=,
∴四边形ABED的面积=(6+12)×6=54.
21.(1)证明:四边形是平行四边形,
,
,
,
在和中,,
.
(2)证明:,
,
四边形是平行四边形,
,
,
在四边形中,,
四边形是矩形.
22.解:(1)证明:∵四边形是矩形
∴,
∴
∵是的中点
∴
在和中
∴
∴
又∵
∴四边形是平行四边形.
(2)解:
证明:∵平分
∴
∴
∵
∴.
23.(1)解:△ACF是等腰三角形,理由如下:
如图,
由折叠可知,∠1=∠2,
∵四边形ABCD是矩形,
∴AB∥CD,
∴∠2=∠3,
∴∠1=∠3,
∴AF=CF,
∴△ACF是等腰三角形;
(2)∵四边形ABCD是矩形且AB=8,BC=4,
∴AD=BC=4,CD=AB=8,∠D=90°,
设FD=x,则AF=CF=8-x,
在Rt△AFD中,根据勾股定理得AD2+DF2=AF2,
∴42+x2=(8-x)2,
解得x=3 ,即DF=3,
∴CF=8-3=5,
∴;
(3)如图,连接PB,
根据折叠得:CE=CB,∠ECP=∠BCP,
∵CP=CP,
∴△ECP≌△BCP,
∴PE=PB,
∴PE+PF=PE+PB,
∴当点F、P、B三点共线时,PE+PF最小,最小值为BF的长,
由(2)知:CF=5,
∵BC=4,∠BCF=90°,
∴ ,
即PE+PF最小值为 .
18.2.1矩形 课后练习
一、选择题
1.矩形具有而一般平行四边形不具有的性质是( )
A.对边平行且相等 B.对角线相等
C.对角线互相平分 D.对角线互相垂直
2.一个矩形的两条对角线的一个夹角为,对角线长为,则这个矩形较短边的长为( )
A. B. C. D.
3.如图,矩形ABCD中,对角线AC和BD交于点O,E为BC中点.若AC=8,∠ACB=30°,则OE的长为( )
A.2 B.3 C.4 D.4
4.如图,矩形中,对角线交于点O,,则矩形的面积是( )
A.2 B. C. D.8
5.如图,矩形ABCD的对角线AC与BD相交于点O,夹角∠AOB=60°,已知AB=1,则△ABD的面积是( )
A.1 B.2 C. D.
6.如图,矩形ABCD中,AB=2BC,点E在CD上,AE=AB,则∠ABE的度数为( )
A.60° B.70° C.72° D.75°
7.已知在矩形ABCD中,对角线AC、BD交于点O,,点E在边AD上,,点F在边BC上,将四边形CDEF沿EF翻折,点D恰好与点O重合,则CF的长为( )
A. B. C. D.
8.如图,在中,,,AD平分交BC于点D,点E为AC的中点,连接DE,则的周长为( )
A.12 B.13 C.14 D.18
9.如图,在中,对角线、相交于点O,且,则的度数为( )
A. B. C. D.
10.如图,AC、BC、BE、DE是四根长度均为10cm的火柴棒,点A、B、D共线.若AB=12cm,BD=16cm,点C和点E之间的距离是( )
A. B. C. D.
二、填空题
11.在矩形ABCD中对角线AC,BD交于点O,且.若,则BC长为_________.
12.在矩形中,,点E在直线上,是以为底的等腰三角形,则线段的长度为_______.
13.如图,在中,,,是的中点,若的周长等于6,则__________.
14.在矩形ABCD中,AB=2,BC=2AB,E是AB上的一点,沿CE将△EBC上翻折,若B点恰好落在边AD上的F点,则AF=______.
15.如图,在矩形ABCD中,AB=3a,BC=4a,若点E是边AD上一点,点F是矩形内一点,∠BCF=30°,则EF+CF的最小值是_____.
三、解答题
16.如图,在矩形ABCD中,,对角线AC、BD相交于点O,求的度数.
17.如图,矩形ABCD中,AB=8,BC=10,△ABF的面积是24,点E为DC边上的一点,将△ADE沿直线AE折叠,点D刚好落在BC边上的点F处,求AE的长.
18.如图,已知 的高 相交于点 分别是 的中点,求证: 垂直平分 .(括号中需写本学期新学理由)
19.如图,在□ABCD中,过点D作于点E,点F在边上,,连接.
(1)求证:四边形是矩形;
(2)已知,若,求的长度.
20.如图,在平行四边形ABCD中,对角线AC、BD相交于点O,BE∥AC交DC的延长线于点E,且BD=BE.
(1)求证:四边形ABCD是矩形;
(2)若∠DBC=30°,BO=6,求四边形ABED的面积.
21.已知:如图,在 ABCD中,AE⊥BC,,点E,F分别为垂足.
(1)求证:△ABE≌△CDF;
(2)求证:四边形AECF是矩形.
22.如图,矩形中,是的中点,延长,交于点,连接,.
(1)求证:四边形是平行四边形;
(2)当平分时,猜想与的数量关系,并证明你的结论.
如图,将矩形纸片ABCD沿对角线AC折叠,使点B落在点E处,AE交CD于点F,且已知AB=8,BC=4
(1)判断△ACF的形状,并说明理由;
(2)求△ACF的面积;
(3)点P为AC上一动点,则PE+PF最小值为________23________.
【参考答案】
1.B 2.C 3.A 4.C 5.C 6.D 7.A 8.C 9.A 10.C
11.
12.
13.4
14.
15.3a
16.解:∵四边形ABCD为矩形,
∴,,,
∵,
∴,
∴,
∴.
17.解:∵四边形ABCD是矩形,AB=8,BC=10,
∴AB=CD=8,BC=AD=10,∠B=∠C=∠D=90°,
∵△ABF的面积是24,
∴,
∴,
∴CF=4,
由折叠的性质可得:DE=EF,
设EF=DE=x,则CE=8-x,
在Rt△ECF中,由勾股定理可得:,
解得:,即,
在Rt△ADE中,.
18.证明:联结,
∵ , ,
∴ ,
∵ 是 的中点 ,
∴ (直角三角形斜边中线等于斜边一半),
∴ ,
∴ 在线段的垂直平分线上 (垂直平分线的逆定理) ,
∴ 垂直平分 .
19.(1)证明:∵四边形是平行四边形,
∴,DC=AB.
∵CF=AE,
∴DF=BE且DF||BE,
∴四边形是平行四边形.
又∵DE⊥AB ,∴∠DEB=90°,
∴四边形是矩形.
(2)解:∵∠ADE=60°,DE⊥AB,
∴∠DAE=30°,
又∵,
∴DE=AD=
20.(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,
又∵点E在DC的延长线上,
∴AB∥CE,
又∵BE∥AC,
∴四边形ABEC是平行四边形,
∴AC=BE,
又BD=BE,
∴AC=BD,
∴平行四边形ABCD是矩形;
(2)解:∵在矩形ABCD中,∠DBC=30°,OA=OB,
∴∠ABD=60°,
∴△AOB是等边三角形,
∴AB=BO=6,
∴BD=2BO=2×6=12,
又∵四边形ABEC是平行四边形,
∴CE=AB=6,
∴DE=CD+CE=12,
在Rt△ABC中,BC=,
∴四边形ABED的面积=(6+12)×6=54.
21.(1)证明:四边形是平行四边形,
,
,
,
在和中,,
.
(2)证明:,
,
四边形是平行四边形,
,
,
在四边形中,,
四边形是矩形.
22.解:(1)证明:∵四边形是矩形
∴,
∴
∵是的中点
∴
在和中
∴
∴
又∵
∴四边形是平行四边形.
(2)解:
证明:∵平分
∴
∴
∵
∴.
23.(1)解:△ACF是等腰三角形,理由如下:
如图,
由折叠可知,∠1=∠2,
∵四边形ABCD是矩形,
∴AB∥CD,
∴∠2=∠3,
∴∠1=∠3,
∴AF=CF,
∴△ACF是等腰三角形;
(2)∵四边形ABCD是矩形且AB=8,BC=4,
∴AD=BC=4,CD=AB=8,∠D=90°,
设FD=x,则AF=CF=8-x,
在Rt△AFD中,根据勾股定理得AD2+DF2=AF2,
∴42+x2=(8-x)2,
解得x=3 ,即DF=3,
∴CF=8-3=5,
∴;
(3)如图,连接PB,
根据折叠得:CE=CB,∠ECP=∠BCP,
∵CP=CP,
∴△ECP≌△BCP,
∴PE=PB,
∴PE+PF=PE+PB,
∴当点F、P、B三点共线时,PE+PF最小,最小值为BF的长,
由(2)知:CF=5,
∵BC=4,∠BCF=90°,
∴ ,
即PE+PF最小值为 .
