2021-2022学年人教版数学九年级下册27.2.1相似三角形的判定课时练习(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版数学九年级下册27.2.1相似三角形的判定课时练习(Word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 530.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-21 14:49:05 | ||
图片预览


文档简介
相似三角形的判定
一、单选题
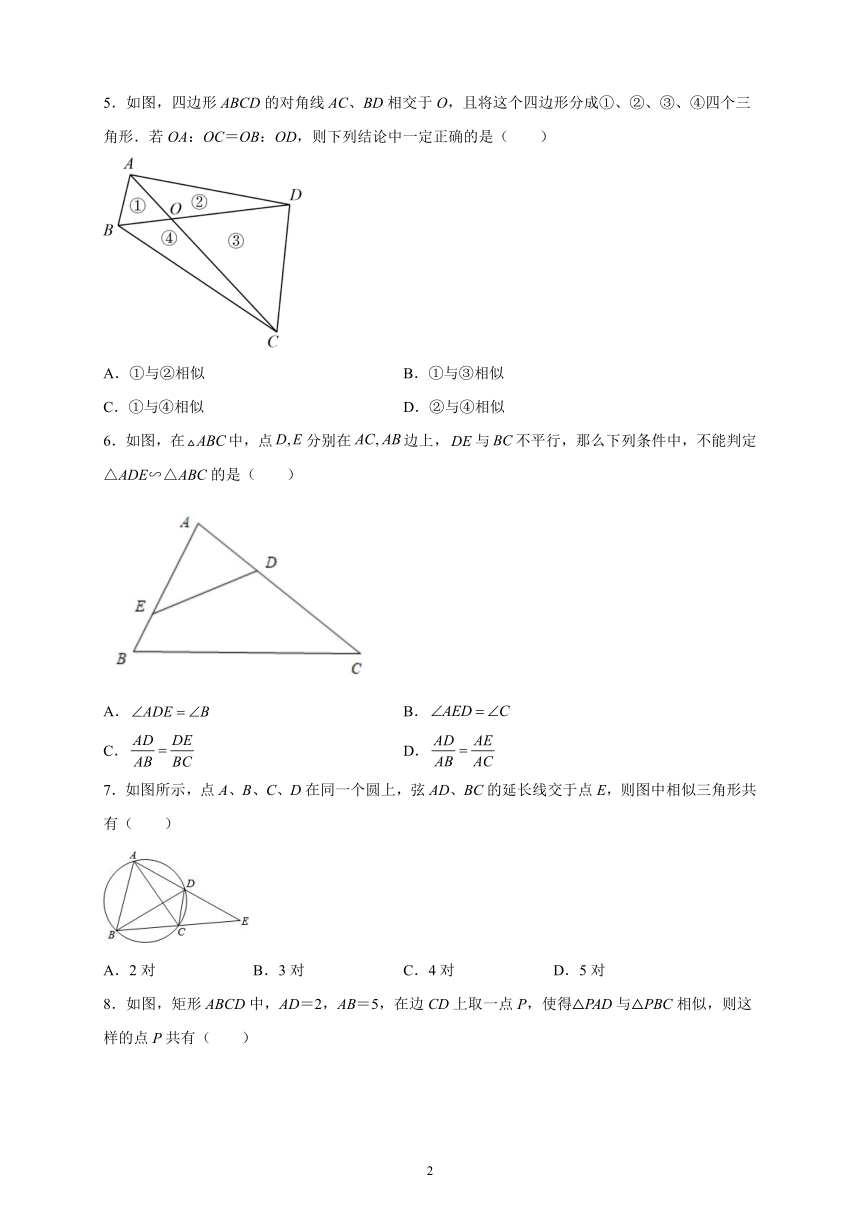
1.如图,小正方形边长均为1,则下列图形中的三角形(阴影)与相似的是( )
A. B. C. D.
2.如图所示,若,则需满足( )
A. B. C. D.
3.如图,在Rt△ABC中,∠CAB=90°,AD⊥CB,两两相似的三角形对数为( )
A.2 B.3 C.4 D.5
4.如图,下列选项中不能判定的是( )
A. B.
C. D.
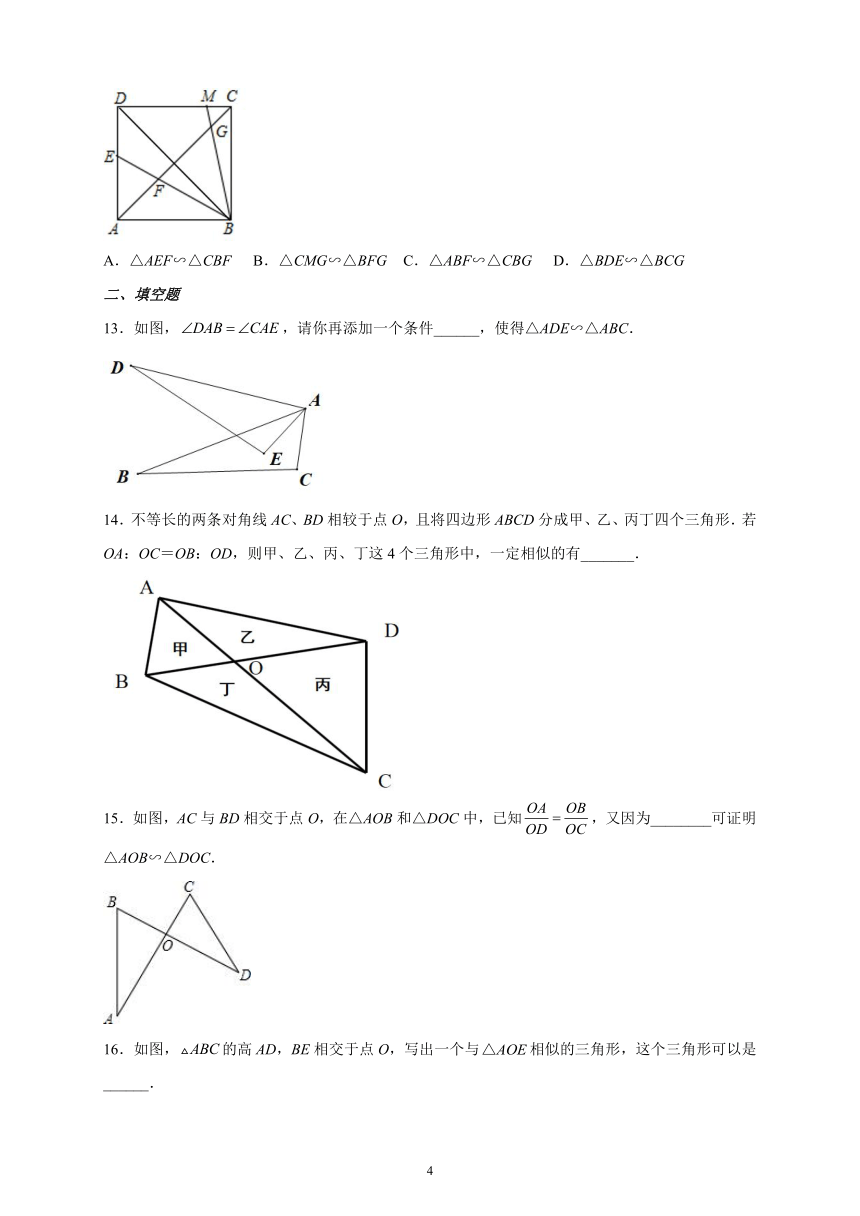
5.如图,四边形ABCD的对角线AC、BD相交于O,且将这个四边形分成①、②、③、④四个三角形.若OA:OC=OB:OD,则下列结论中一定正确的是( )
A.①与②相似 B.①与③相似
C.①与④相似 D.②与④相似
6.如图,在中,点分别在边上,与不平行,那么下列条件中,不能判定△ADE∽△ABC的是( )
A. B.
C. D.
7.如图所示,点A、B、C、D在同一个圆上,弦AD、BC的延长线交于点E,则图中相似三角形共有( )
A.2对 B.3对 C.4对 D.5对
8.如图,矩形ABCD中,AD=2,AB=5,在边CD上取一点P,使得△PAD与△PBC相似,则这样的点P共有( )
A.1个 B.2个 C.3个 D.4个
9.如图,在△ABC中,DE∥BC,MN∥AB,则图中与△ABC相似的三角形有( )
A.1个 B.2个 C.3个 D.4个
10.将两个完全相同的等腰直角三角形△ABC与△AFG摆成如图的样子,两个三角形的重叠部分为△ADE,那么图中一定相似的三角形是( )
A.△ABC与△ADE B.△ABD与△AEC C.△ABE与△ACD D.△AEC与△ADC
11.如图,点D、E分别在的边AB、AC的反向延长线上,下面比例式中,不一定能判断的是( )
A. B.
C. D.
12.如图,在正方形ABCD中,点E为AD边上的一个动点(与点A,D不重合),∠EBM=45°,BE交对角线AC于点F,BM交对角线AC于点G,交CD于点M,下列结论中错误的是( )
A.△AEF∽△CBF B.△CMG∽△BFG C.△ABF∽△CBG D.△BDE∽△BCG
二、填空题
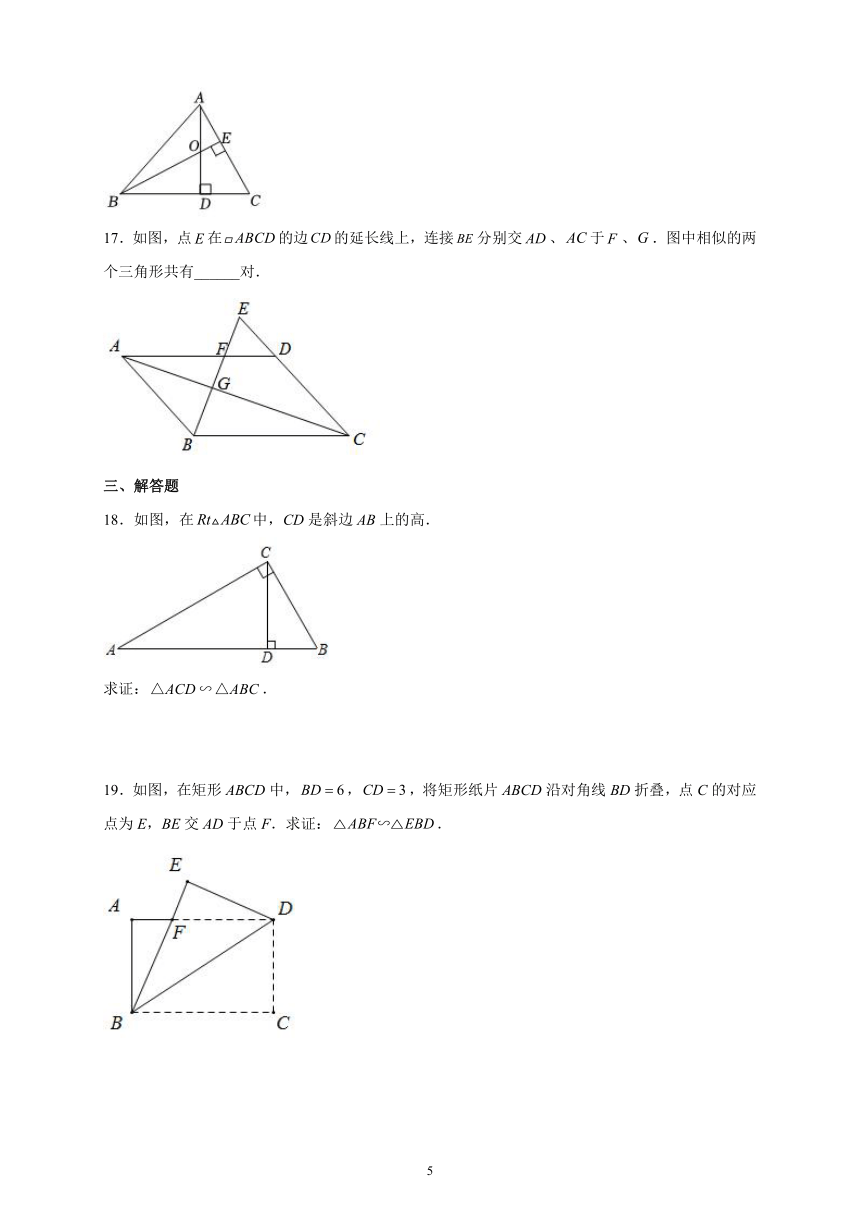
13.如图,,请你再添加一个条件______,使得△ADE∽△ABC.
14.不等长的两条对角线AC、BD相较于点O,且将四边形ABCD分成甲、乙、丙丁四个三角形.若OA:OC=OB:OD,则甲、乙、丙、丁这4个三角形中,一定相似的有_______.
15.如图,AC与BD相交于点O,在△AOB和△DOC中,已知,又因为________可证明△AOB∽△DOC.
16.如图,的高AD,BE相交于点O,写出一个与相似的三角形,这个三角形可以是______.
17.如图,点在的边的延长线上,连接分别交、于、.图中相似的两个三角形共有______对.
三、解答题
18.如图,在中,CD是斜边AB上的高.
求证:.
19.如图,在矩形ABCD中,,,将矩形纸片ABCD沿对角线BD折叠,点C的对应点为E,BE交AD于点F.求证:.
20.如图,在△ABC中,点D、E、F分别在AB、BC、AC边上,DE∥AC,∠DEF=∠A.求证:△BDE∽△EFC.
21.如图,在中,,,BD为角平分线,,垂足为E.
(1)证明;
(2)证明.
22.如图,在矩形ABCD中,点E,F分别在CD,AD上,连结AE,BF,AE⊥BF且AE=BF.
(1)求证:AB=AD.
(2)连结EF,BE,线段FD是线段AD与AF的比例中项.
①若AD=4,求线段FD的长.
②求证:△DEF∽△CEB.
23.如图,已知矩形OABC中,OA=2,AB=4,双曲线(k>0)与矩形两边AB、BC分别交于E、F.
(1)若E是AB的中点,求F点的坐标;
(2)若将△BEF沿直线EF对折,B点落在x轴上的D点,作EG⊥OC,垂足为G,求证:△EGD∽△DCF.
(3)在第(2)的条件下求k的值.
试卷第1页,共3页
参考答案:
1.C
解:由正方形的性质可知,∠ABC=180°-45°=135°,
A、B、D图形中的钝角都不等于135°,
由勾股定理得,BC=,AB=2,
对应的图形C中的边长分别为和1,
∵,
∴图C中的三角形(阴影部分)与△ABC相似,
故选:C.
2.B
解:是公共角,要使
只需,即
故选:B.
3.B
解:∵AD⊥CB,
∴∠ADC=∠BDA=90°,
∴∠BAC=∠ADC=90°
又∵∠C=∠C,
∴△ADC∽△BAC,
同理:△ADB∽△CAB,
∴△ADC∽△BAC∽△BDA,
故选:B.
4.B
解:根据题意得:∠A=∠A,
A、若,可利用有两角相等的两个三角形相似判定,故本选项不符合题意;
B、若,则,不能判定,故本选项符合题意;
C、若,则,可利用两边对应成比例及其夹角相等的两个三角形相似判定,故本选项不符合题意;
D、若,可利用有两角相等的两个三角形相似判定,故本选项不符合题意;
故选:B
5.B
解:∵OA:OC=OB:OD,
∠AOB=∠COD(对顶角相等),
∴①与③相似.
故选:B.
6.C
解:根据题意得:∠A=∠A,
A、,可利用两角对应相等的两个三角形相似,故本选项不符合题意;
B、,可利用两角对应相等的两个三角形相似,故本选项不符合题意;
C、,不能判定两个三角形相似,故本选项符合题意;
D、,可利用两边对应成比例,及其夹角对应相等的两个三角形相似,故本选项不符合题意;
故选:C
7.C
解:取的交点为,如下图:
为公共角,根据同弧所对的圆周角相等,
,可得,
又由于,可得,
由,,可得,
由,,可得,
故选:C.
8.C
解:如图,以AB为直径作⊙O交CD于点P1,P2,连接AP1,BP1,AP2,BP2.
∵AB为⊙O直径,
∴ ,
∴ ,
为矩形, ,
∴ ,
∴ ,
∴△ADP1∽△P1CB,
同理△ADP2∽△P2CB,
取CD的中点P3,连接AP3,BP3,则同理△ADP3∽△P3CB,
故选:C.
9.C
解:如图,
根据题意,DE∥BC,MN∥AB,
可得△ADE,△MNC,△MGE均与△ABC相似,共3个,
故选:C.
10.C
解:A.是直角三角形,不是直角三角形,故不能判断△ABC与△ADE相似;
B.只有,不能判断B选项中△ABD与△AEC相似;
D. 只有,不能判断D选项中△AEC与△ADC相似;
C.是等腰直角三角形,则
设,则,
,
,
,
△ABE与△DCA
故选C.
11.C
解:对于A选项.
∵,
∴.
∴.
∴.
又∵,
∴.
∴.
∴.
故A选项不符合题意.
对于B选项.
∵,,
∴.
∴.
∴.
故B选项不符合题意.
对于D选项.
∵,
∴.
又∵,
∴.
∴.
∴.
故D选项不符合题意.
故选:C.
12.C
解:∵四边形ABCD是正方形,
∴AB∥CD,AD∥BC,∠DCA=∠ACB=∠DAC=∠CAB=∠EBM=45°,
∴△AEF∽△CBF,故选项A不合题意;
∵∠EBM=∠DCA,∠MGC=∠BGF,
∴△CMG∽△BFG,故选项B不合题意;
∵∠CAB=∠ACB=∠FBG=45°,
∴∠ABF+∠CBG=45°,
∴∠ABF与∠CBG不一定相等,
∴△ABF与△CBG不一定相似,
故选项C符合题意;
△BDE∽△BCG,故D不符合题意;
故选:C.
13.(答案不唯一)
解:∵,
∴,
即,
∴当或或或时两三角形相似.
故答案为:(答案不唯一).
14.甲和丙
解:略
15.∠AOB=∠DOC
解:略
16.(答案不唯一)
解:本题答案不唯一;
与相似的三角形有:,,,
选择求证:.
证明:的高,交于点,
.
,
,
故答案是:.
17.6
解:是平行四边形,
,,
,,,,五对,还有一对特殊的相似三角形即,
共6对,
故答案是;6.
18.见解析
证明:如图,
∵在中,CD是斜边AB上的高
∴
∵是公共角
∴.
19.证明见解析
证明: 矩形ABCD,
由折叠可得:
20.见解析
解:证明,
,
又,
,
,
,
.
21.(1)见解析 (2)见解析
(1)
证明:∵,,
∴,
∵BD为角平分线,
∴,
在和中,
∵,
∴
(2)
证明:∵,,
∴,
∵BD为角平分线,
∴,
∵,
∴.
22.(1)见解析 (2)①; ②见解析
(1)
解:∵四边形ABCD是矩形,
∴∠BAD=∠ADE=90°,
∴∠ABF+∠AFB=90°,
∵AE⊥BF,
∴∠DAE+∠AFB=90°,
∴∠ABF=∠DAE,
在△ABF和△DAE中,
,
∴△ABF≌△DAE(AAS),
∴AB=AD;
(2)
①∵线段FD是线段AD与AF的比例中项
∴FD2=AD·AF,
∵AD=4,设FD=x,则AF=4-x,
∴x2=4(4-x),
解得:x=或(舍),
∴FD=;
②由(1)可知,△ABF≌△DAE,
∴AF=DE,
∴DF=CE,
∵线段DF是线段AF与AD的比例中项,
∴DF2=AF AD,
∴,
∵∠FDE=∠BCE=90°,
∴△FDE∽△BCE.
23.(1);(2)见解析;(3)
解:(1)∵点E是的中点,,,
∴点E的坐标为,
将点E的坐标代入,可得,
∴反比例函数解析式为:,
∵点F的横坐标为4,
∴点F的纵坐标,
∴点F的坐标为;
(2)由折叠的性质可得:,,,
∵,,
∴,
又∵,
∴;
(3)结合图形可设点E坐标为,点F坐标为,
则,
在中,
∵,
∴,即,
∴,
解得:.
答案第1页,共2页
一、单选题
1.如图,小正方形边长均为1,则下列图形中的三角形(阴影)与相似的是( )
A. B. C. D.
2.如图所示,若,则需满足( )
A. B. C. D.
3.如图,在Rt△ABC中,∠CAB=90°,AD⊥CB,两两相似的三角形对数为( )
A.2 B.3 C.4 D.5
4.如图,下列选项中不能判定的是( )
A. B.
C. D.
5.如图,四边形ABCD的对角线AC、BD相交于O,且将这个四边形分成①、②、③、④四个三角形.若OA:OC=OB:OD,则下列结论中一定正确的是( )
A.①与②相似 B.①与③相似
C.①与④相似 D.②与④相似
6.如图,在中,点分别在边上,与不平行,那么下列条件中,不能判定△ADE∽△ABC的是( )
A. B.
C. D.
7.如图所示,点A、B、C、D在同一个圆上,弦AD、BC的延长线交于点E,则图中相似三角形共有( )
A.2对 B.3对 C.4对 D.5对
8.如图,矩形ABCD中,AD=2,AB=5,在边CD上取一点P,使得△PAD与△PBC相似,则这样的点P共有( )
A.1个 B.2个 C.3个 D.4个
9.如图,在△ABC中,DE∥BC,MN∥AB,则图中与△ABC相似的三角形有( )
A.1个 B.2个 C.3个 D.4个
10.将两个完全相同的等腰直角三角形△ABC与△AFG摆成如图的样子,两个三角形的重叠部分为△ADE,那么图中一定相似的三角形是( )
A.△ABC与△ADE B.△ABD与△AEC C.△ABE与△ACD D.△AEC与△ADC
11.如图,点D、E分别在的边AB、AC的反向延长线上,下面比例式中,不一定能判断的是( )
A. B.
C. D.
12.如图,在正方形ABCD中,点E为AD边上的一个动点(与点A,D不重合),∠EBM=45°,BE交对角线AC于点F,BM交对角线AC于点G,交CD于点M,下列结论中错误的是( )
A.△AEF∽△CBF B.△CMG∽△BFG C.△ABF∽△CBG D.△BDE∽△BCG
二、填空题
13.如图,,请你再添加一个条件______,使得△ADE∽△ABC.
14.不等长的两条对角线AC、BD相较于点O,且将四边形ABCD分成甲、乙、丙丁四个三角形.若OA:OC=OB:OD,则甲、乙、丙、丁这4个三角形中,一定相似的有_______.
15.如图,AC与BD相交于点O,在△AOB和△DOC中,已知,又因为________可证明△AOB∽△DOC.
16.如图,的高AD,BE相交于点O,写出一个与相似的三角形,这个三角形可以是______.
17.如图,点在的边的延长线上,连接分别交、于、.图中相似的两个三角形共有______对.
三、解答题
18.如图,在中,CD是斜边AB上的高.
求证:.
19.如图,在矩形ABCD中,,,将矩形纸片ABCD沿对角线BD折叠,点C的对应点为E,BE交AD于点F.求证:.
20.如图,在△ABC中,点D、E、F分别在AB、BC、AC边上,DE∥AC,∠DEF=∠A.求证:△BDE∽△EFC.
21.如图,在中,,,BD为角平分线,,垂足为E.
(1)证明;
(2)证明.
22.如图,在矩形ABCD中,点E,F分别在CD,AD上,连结AE,BF,AE⊥BF且AE=BF.
(1)求证:AB=AD.
(2)连结EF,BE,线段FD是线段AD与AF的比例中项.
①若AD=4,求线段FD的长.
②求证:△DEF∽△CEB.
23.如图,已知矩形OABC中,OA=2,AB=4,双曲线(k>0)与矩形两边AB、BC分别交于E、F.
(1)若E是AB的中点,求F点的坐标;
(2)若将△BEF沿直线EF对折,B点落在x轴上的D点,作EG⊥OC,垂足为G,求证:△EGD∽△DCF.
(3)在第(2)的条件下求k的值.
试卷第1页,共3页
参考答案:
1.C
解:由正方形的性质可知,∠ABC=180°-45°=135°,
A、B、D图形中的钝角都不等于135°,
由勾股定理得,BC=,AB=2,
对应的图形C中的边长分别为和1,
∵,
∴图C中的三角形(阴影部分)与△ABC相似,
故选:C.
2.B
解:是公共角,要使
只需,即
故选:B.
3.B
解:∵AD⊥CB,
∴∠ADC=∠BDA=90°,
∴∠BAC=∠ADC=90°
又∵∠C=∠C,
∴△ADC∽△BAC,
同理:△ADB∽△CAB,
∴△ADC∽△BAC∽△BDA,
故选:B.
4.B
解:根据题意得:∠A=∠A,
A、若,可利用有两角相等的两个三角形相似判定,故本选项不符合题意;
B、若,则,不能判定,故本选项符合题意;
C、若,则,可利用两边对应成比例及其夹角相等的两个三角形相似判定,故本选项不符合题意;
D、若,可利用有两角相等的两个三角形相似判定,故本选项不符合题意;
故选:B
5.B
解:∵OA:OC=OB:OD,
∠AOB=∠COD(对顶角相等),
∴①与③相似.
故选:B.
6.C
解:根据题意得:∠A=∠A,
A、,可利用两角对应相等的两个三角形相似,故本选项不符合题意;
B、,可利用两角对应相等的两个三角形相似,故本选项不符合题意;
C、,不能判定两个三角形相似,故本选项符合题意;
D、,可利用两边对应成比例,及其夹角对应相等的两个三角形相似,故本选项不符合题意;
故选:C
7.C
解:取的交点为,如下图:
为公共角,根据同弧所对的圆周角相等,
,可得,
又由于,可得,
由,,可得,
由,,可得,
故选:C.
8.C
解:如图,以AB为直径作⊙O交CD于点P1,P2,连接AP1,BP1,AP2,BP2.
∵AB为⊙O直径,
∴ ,
∴ ,
为矩形, ,
∴ ,
∴ ,
∴△ADP1∽△P1CB,
同理△ADP2∽△P2CB,
取CD的中点P3,连接AP3,BP3,则同理△ADP3∽△P3CB,
故选:C.
9.C
解:如图,
根据题意,DE∥BC,MN∥AB,
可得△ADE,△MNC,△MGE均与△ABC相似,共3个,
故选:C.
10.C
解:A.是直角三角形,不是直角三角形,故不能判断△ABC与△ADE相似;
B.只有,不能判断B选项中△ABD与△AEC相似;
D. 只有,不能判断D选项中△AEC与△ADC相似;
C.是等腰直角三角形,则
设,则,
,
,
,
△ABE与△DCA
故选C.
11.C
解:对于A选项.
∵,
∴.
∴.
∴.
又∵,
∴.
∴.
∴.
故A选项不符合题意.
对于B选项.
∵,,
∴.
∴.
∴.
故B选项不符合题意.
对于D选项.
∵,
∴.
又∵,
∴.
∴.
∴.
故D选项不符合题意.
故选:C.
12.C
解:∵四边形ABCD是正方形,
∴AB∥CD,AD∥BC,∠DCA=∠ACB=∠DAC=∠CAB=∠EBM=45°,
∴△AEF∽△CBF,故选项A不合题意;
∵∠EBM=∠DCA,∠MGC=∠BGF,
∴△CMG∽△BFG,故选项B不合题意;
∵∠CAB=∠ACB=∠FBG=45°,
∴∠ABF+∠CBG=45°,
∴∠ABF与∠CBG不一定相等,
∴△ABF与△CBG不一定相似,
故选项C符合题意;
△BDE∽△BCG,故D不符合题意;
故选:C.
13.(答案不唯一)
解:∵,
∴,
即,
∴当或或或时两三角形相似.
故答案为:(答案不唯一).
14.甲和丙
解:略
15.∠AOB=∠DOC
解:略
16.(答案不唯一)
解:本题答案不唯一;
与相似的三角形有:,,,
选择求证:.
证明:的高,交于点,
.
,
,
故答案是:.
17.6
解:是平行四边形,
,,
,,,,五对,还有一对特殊的相似三角形即,
共6对,
故答案是;6.
18.见解析
证明:如图,
∵在中,CD是斜边AB上的高
∴
∵是公共角
∴.
19.证明见解析
证明: 矩形ABCD,
由折叠可得:
20.见解析
解:证明,
,
又,
,
,
,
.
21.(1)见解析 (2)见解析
(1)
证明:∵,,
∴,
∵BD为角平分线,
∴,
在和中,
∵,
∴
(2)
证明:∵,,
∴,
∵BD为角平分线,
∴,
∵,
∴.
22.(1)见解析 (2)①; ②见解析
(1)
解:∵四边形ABCD是矩形,
∴∠BAD=∠ADE=90°,
∴∠ABF+∠AFB=90°,
∵AE⊥BF,
∴∠DAE+∠AFB=90°,
∴∠ABF=∠DAE,
在△ABF和△DAE中,
,
∴△ABF≌△DAE(AAS),
∴AB=AD;
(2)
①∵线段FD是线段AD与AF的比例中项
∴FD2=AD·AF,
∵AD=4,设FD=x,则AF=4-x,
∴x2=4(4-x),
解得:x=或(舍),
∴FD=;
②由(1)可知,△ABF≌△DAE,
∴AF=DE,
∴DF=CE,
∵线段DF是线段AF与AD的比例中项,
∴DF2=AF AD,
∴,
∵∠FDE=∠BCE=90°,
∴△FDE∽△BCE.
23.(1);(2)见解析;(3)
解:(1)∵点E是的中点,,,
∴点E的坐标为,
将点E的坐标代入,可得,
∴反比例函数解析式为:,
∵点F的横坐标为4,
∴点F的纵坐标,
∴点F的坐标为;
(2)由折叠的性质可得:,,,
∵,,
∴,
又∵,
∴;
(3)结合图形可设点E坐标为,点F坐标为,
则,
在中,
∵,
∴,即,
∴,
解得:.
答案第1页,共2页
