2021-2022学年人教版九年级下册数学27.2.2相似三角形的性质巩固练习(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版九年级下册数学27.2.2相似三角形的性质巩固练习(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 598.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-21 00:00:00 | ||
图片预览


文档简介
2021-2022学年九年级下册数学巩固练习(人教版)
27.2.2相似三角形的性质
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.若,相似比为,则与对应的中线之比为( )
A.4:3 B.3:4 C.16:9 D.9:16
2.要制作两个形状相同的三角形框架,其中一个三角形的三边长分别为5 cm,6 cm和9 cm,另一个三角形的最短边长为2.5 cm,则它的最长边为( )
A.3 cm B.4 cm C.4.5 cm D.5 cm
3.已知,AD和是它们的对应中线,若,,则与的周长比是( )
A.3:5 B.9:25 C.5:3 D.25:9
4.如图,已知,,则下列等式一定成立的是( )
A. B. C. D.
5.如图,在中,点D在上、点E在上,若,,,则等于( )
A.52° B.62° C.68° D.72°
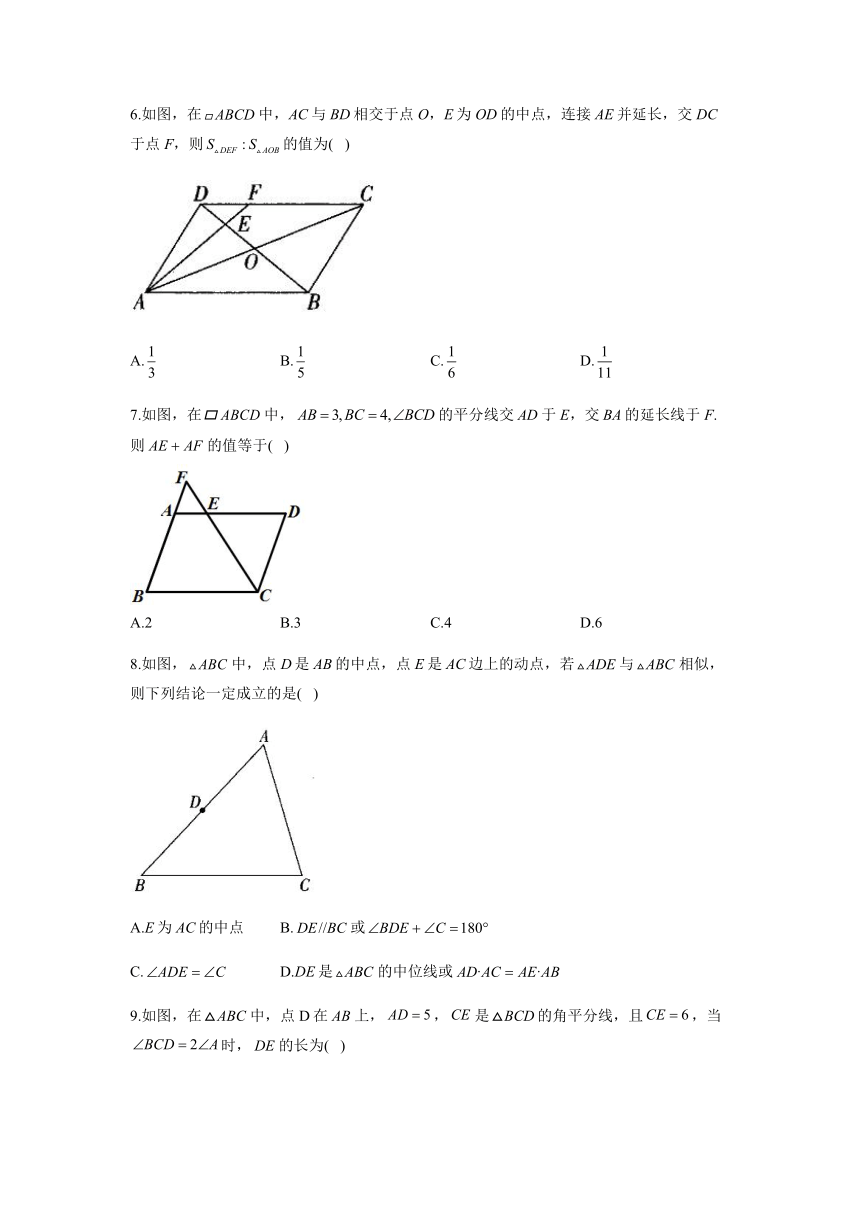
6.如图,在中,AC与BD相交于点O,E为OD的中点,连接AE并延长,交DC于点F,则的值为( )
A. B. C. D.
7.如图,在中,的平分线交于E,交的延长线于F.则的值等于( )
A.2 B.3 C.4 D.6
8.如图,中,点D是AB的中点,点E是AC边上的动点,若与相似,则下列结论一定成立的是( )
A.E为AC的中点 B.或
C. D.DE是的中位线或
9.如图,在中,点D在上,,是的角平分线,且,当时,的长为( )
A.3 B.4 C.5 D.6
二、填空题
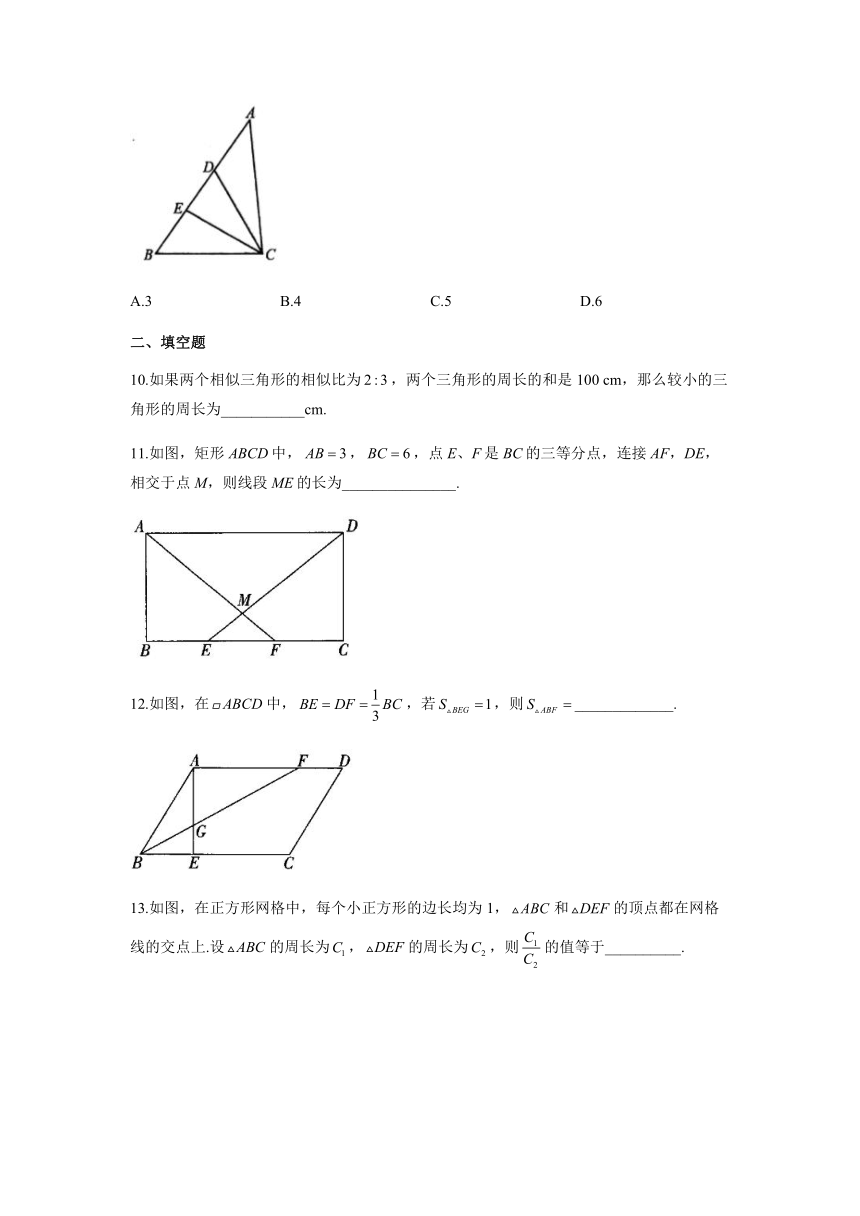
10.如果两个相似三角形的相似比为,两个三角形的周长的和是100 cm,那么较小的三角形的周长为___________cm.
11.如图,矩形ABCD中,,,点E、F是BC的三等分点,连接AF,DE,相交于点M,则线段ME的长为_______________.
12.如图,在中,,若,则_____________.
13.如图,在正方形网格中,每个小正方形的边长均为1,和的顶点都在网格线的交点上.设的周长为,的周长为,则的值等于__________.
14.如图,四边形ABCD中,,CM是的平分线,且,M为垂足,.若四边形图ABCD的面积为,则四边形AMCD的面积是___________.
三、解答题
15.“今有井径五尺,不知其深,立五尺于井上,从木末望水岸,入径2尺,问井深几何?”这是我国古代数学《九章算术》中的“井深几何”问题,它的题意可以由图获得,请你求井深.
16.如图,已知,.
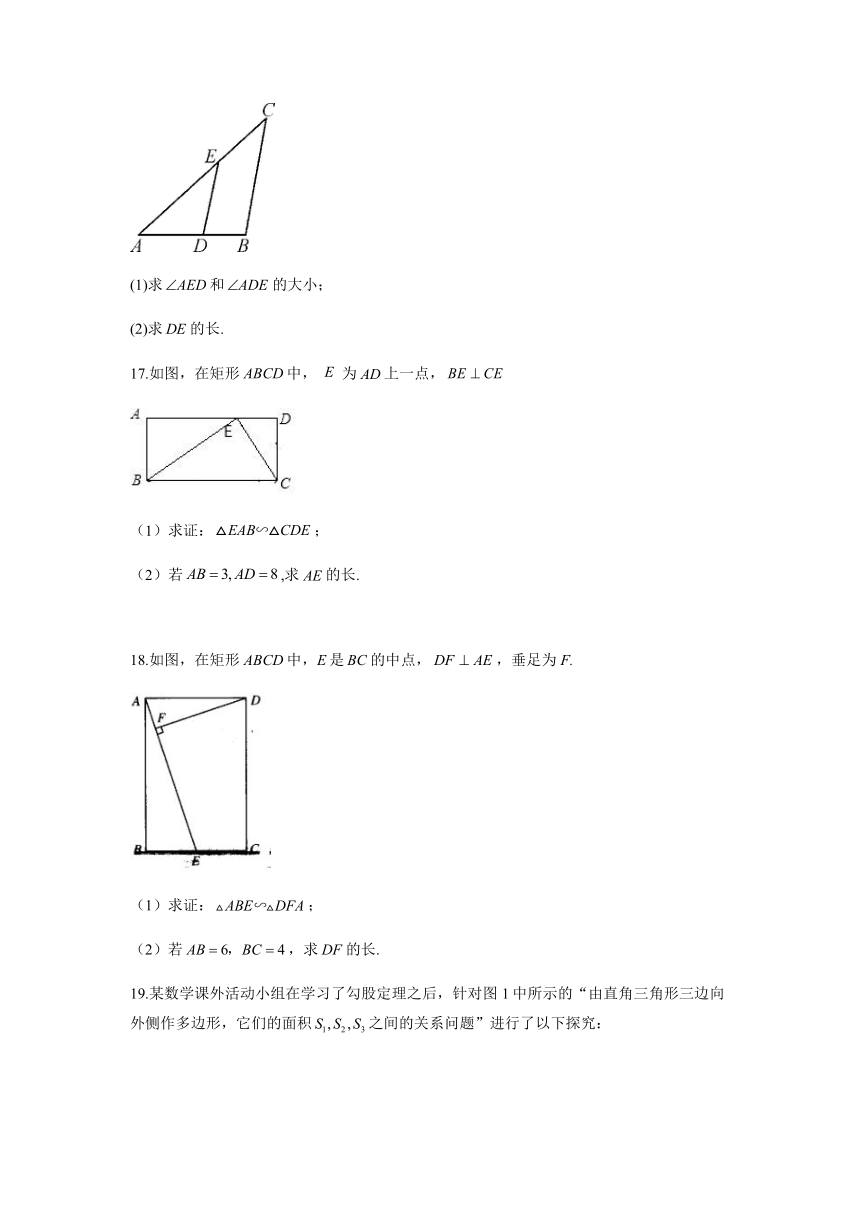
(1)求和的大小;
(2)求的长.
17.如图,在矩形中,为上一点,
(1)求证:;
(2)若,求的长.
18.如图,在矩形中,E是的中点,,垂足为F.
(1)求证:;
(2)若,求的长.
19.某数学课外活动小组在学习了勾股定理之后,针对图1中所示的“由直角三角形三边向外侧作多边形,它们的面积之间的关系问题”进行了以下探究:
类比探究
(1)如图2,在中,为斜边,分别以为斜边向外侧作,若,则面积之间的关系式为__________;
推广验证
(2)如图3,在中,为斜边,分别以为边向外侧作任意,满足,则(1)中所得关系式是否仍然成立?若成立,请证明你的结论;若不成立,请说明理由;
拓展应用
(3)如图4,在五边形中,,,点在上,,求五边形的面积.
参考答案
1.答案:A
解析:,相似比为,与对应的中线之比为.故选A.
2.答案:C
解析:本题考查相似三角形的性质.根据题意可知两个三角形相似,设最长边为x cm,则,解得,即这个三角形的最长边为4.5 cm,故选C.
3.答案:C
解析:,AD和是它们的对应中线,,,与的周长比.故选C.
4.答案:D
解析:,,,A不一定成立;
,B不成立;
,C不成立;
,D成立,故选D.
5.答案:A
解析:
6.答案:C
解析:O为平行四边形ABCD对角线的交点,
,
又E为OD的中点,
,.,,,.,,.故选C.
7.答案:A
解析:
8.答案:B
解析:与相似,分两种情况:当时,,,此时E为AC的中点,DE是的中位线,也可得;当时,,.选项A,C,D中只考虑了一种情况,不一定成立,选项B包含两种情况,一定成立.故选B.
9.答案:B
解析:设,则,
是的角平分线,
,
,,即
整理得,
解得,,
,
即DE的长为:4.
故选:B.
10.答案:40
解析:设较小的三角形的周长为x cm,则较大的三角形的周长为cm,两个相似角形的相似比为,两个相似三角形的周长比为,,解得,即较小的三角形的周长为40 cm.
11.答案:
解析:矩形ABCD中,,,点E、F是BC的三等分点,,,,,在中,.,,,即,.
12.答案:6
解析:在中,,.,.,,.,.,,,,.
13.答案:
解析:由题图及勾股定理得,,,,,.,,,,,.
14.答案:1
解析:如图,延长BA、CD,交点为E.CM平分,,,又,,.,,.,,,.
15.答案:解:依题意可得:,
,
即,
解得:,
尺.
所以井深为7.5尺.
解析:
16.答案:(1).
,,即,.
解析:
17.答案:(1)证明:在矩形中,
(2)由(1)可知
则
即
解得
即的边是
解析:
18.答案:(1)证明:∵四边形是矩形,
.
.
.
.
.
(2).
,E是的中点,
.
∴在中,.
又.
,
.
解析:
19.答案:(1);
(2)成立;
,
.
.
.
为,
.
.
成立.
(3)过点作于点.
连接.
又,
.
连接.
.
,
.
,
.
,
.
.
.
解析:
27.2.2相似三角形的性质
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.若,相似比为,则与对应的中线之比为( )
A.4:3 B.3:4 C.16:9 D.9:16
2.要制作两个形状相同的三角形框架,其中一个三角形的三边长分别为5 cm,6 cm和9 cm,另一个三角形的最短边长为2.5 cm,则它的最长边为( )
A.3 cm B.4 cm C.4.5 cm D.5 cm
3.已知,AD和是它们的对应中线,若,,则与的周长比是( )
A.3:5 B.9:25 C.5:3 D.25:9
4.如图,已知,,则下列等式一定成立的是( )
A. B. C. D.
5.如图,在中,点D在上、点E在上,若,,,则等于( )
A.52° B.62° C.68° D.72°
6.如图,在中,AC与BD相交于点O,E为OD的中点,连接AE并延长,交DC于点F,则的值为( )
A. B. C. D.
7.如图,在中,的平分线交于E,交的延长线于F.则的值等于( )
A.2 B.3 C.4 D.6
8.如图,中,点D是AB的中点,点E是AC边上的动点,若与相似,则下列结论一定成立的是( )
A.E为AC的中点 B.或
C. D.DE是的中位线或
9.如图,在中,点D在上,,是的角平分线,且,当时,的长为( )
A.3 B.4 C.5 D.6
二、填空题
10.如果两个相似三角形的相似比为,两个三角形的周长的和是100 cm,那么较小的三角形的周长为___________cm.
11.如图,矩形ABCD中,,,点E、F是BC的三等分点,连接AF,DE,相交于点M,则线段ME的长为_______________.
12.如图,在中,,若,则_____________.
13.如图,在正方形网格中,每个小正方形的边长均为1,和的顶点都在网格线的交点上.设的周长为,的周长为,则的值等于__________.
14.如图,四边形ABCD中,,CM是的平分线,且,M为垂足,.若四边形图ABCD的面积为,则四边形AMCD的面积是___________.
三、解答题
15.“今有井径五尺,不知其深,立五尺于井上,从木末望水岸,入径2尺,问井深几何?”这是我国古代数学《九章算术》中的“井深几何”问题,它的题意可以由图获得,请你求井深.
16.如图,已知,.
(1)求和的大小;
(2)求的长.
17.如图,在矩形中,为上一点,
(1)求证:;
(2)若,求的长.
18.如图,在矩形中,E是的中点,,垂足为F.
(1)求证:;
(2)若,求的长.
19.某数学课外活动小组在学习了勾股定理之后,针对图1中所示的“由直角三角形三边向外侧作多边形,它们的面积之间的关系问题”进行了以下探究:
类比探究
(1)如图2,在中,为斜边,分别以为斜边向外侧作,若,则面积之间的关系式为__________;
推广验证
(2)如图3,在中,为斜边,分别以为边向外侧作任意,满足,则(1)中所得关系式是否仍然成立?若成立,请证明你的结论;若不成立,请说明理由;
拓展应用
(3)如图4,在五边形中,,,点在上,,求五边形的面积.
参考答案
1.答案:A
解析:,相似比为,与对应的中线之比为.故选A.
2.答案:C
解析:本题考查相似三角形的性质.根据题意可知两个三角形相似,设最长边为x cm,则,解得,即这个三角形的最长边为4.5 cm,故选C.
3.答案:C
解析:,AD和是它们的对应中线,,,与的周长比.故选C.
4.答案:D
解析:,,,A不一定成立;
,B不成立;
,C不成立;
,D成立,故选D.
5.答案:A
解析:
6.答案:C
解析:O为平行四边形ABCD对角线的交点,
,
又E为OD的中点,
,.,,,.,,.故选C.
7.答案:A
解析:
8.答案:B
解析:与相似,分两种情况:当时,,,此时E为AC的中点,DE是的中位线,也可得;当时,,.选项A,C,D中只考虑了一种情况,不一定成立,选项B包含两种情况,一定成立.故选B.
9.答案:B
解析:设,则,
是的角平分线,
,
,,即
整理得,
解得,,
,
即DE的长为:4.
故选:B.
10.答案:40
解析:设较小的三角形的周长为x cm,则较大的三角形的周长为cm,两个相似角形的相似比为,两个相似三角形的周长比为,,解得,即较小的三角形的周长为40 cm.
11.答案:
解析:矩形ABCD中,,,点E、F是BC的三等分点,,,,,在中,.,,,即,.
12.答案:6
解析:在中,,.,.,,.,.,,,,.
13.答案:
解析:由题图及勾股定理得,,,,,.,,,,,.
14.答案:1
解析:如图,延长BA、CD,交点为E.CM平分,,,又,,.,,.,,,.
15.答案:解:依题意可得:,
,
即,
解得:,
尺.
所以井深为7.5尺.
解析:
16.答案:(1).
,,即,.
解析:
17.答案:(1)证明:在矩形中,
(2)由(1)可知
则
即
解得
即的边是
解析:
18.答案:(1)证明:∵四边形是矩形,
.
.
.
.
.
(2).
,E是的中点,
.
∴在中,.
又.
,
.
解析:
19.答案:(1);
(2)成立;
,
.
.
.
为,
.
.
成立.
(3)过点作于点.
连接.
又,
.
连接.
.
,
.
,
.
,
.
.
.
解析:
