2021—2022学年人教版八年级数学下册18.1.1平行四边形的性质课后练习(Word版含答案)
文档属性
| 名称 | 2021—2022学年人教版八年级数学下册18.1.1平行四边形的性质课后练习(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 230.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-21 14:51:44 | ||
图片预览

文档简介
2021——2022学年度人教版八年级数学下册 第十八章 平行四边形
18.1.1 平行四边形的性质 课后练习
一、选择题
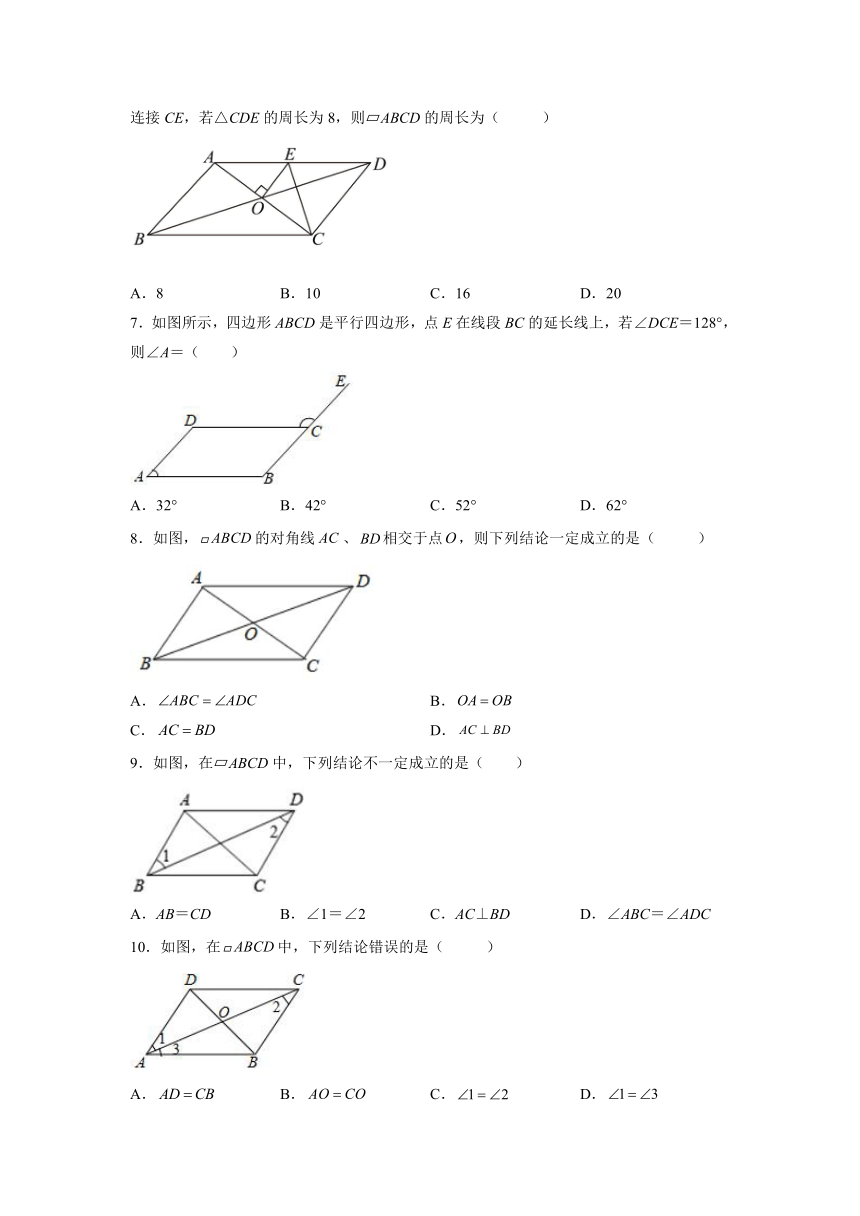
1.在 ABCD中,对角线AC与BD相交于点O,△BOC的周长为20cm,BC=12cm,则AC+BD的长是( )
A.8cm B.16cm C.24cm D.32cm
2.平行四边形的两条对角线将此平行四边形分成全等三角形的对数是( ).
A.2对 B.3对 C.4对 D.5对
3.在平行四边形ABCD中,AE⊥BC于E,AF⊥CD于F,AE=4,AF=6,平行四边形ABCD的周长为40,则平行四边形ABCD的面积是( )
A.36 B.48 C.40 D.24
4.如图,在平行四边形OABC中,对角线相交于点E,OA边在x轴上,点O为坐标原点,已知点,,则点C的坐标为( )
A. B. C. D.
5.如图,将平行四边形ABCD沿对角线AC折叠,使点B落在点处,若,为( )
A.36° B.144° C.108° D.126°
6.如图,在 ABCD中,对角线AC、BD相交于点O,过点O作OE⊥AC,交AD于点E,连接CE,若△CDE的周长为8,则 ABCD的周长为( )
A.8 B.10 C.16 D.20
7.如图所示,四边形ABCD是平行四边形,点E在线段BC的延长线上,若∠DCE=128°,则∠A=( )
A.32° B.42° C.52° D.62°
8.如图,的对角线、相交于点,则下列结论一定成立的是( )
A. B.
C. D.
9.如图,在 ABCD中,下列结论不一定成立的是( )
A.AB=CD B.∠1=∠2 C.AC⊥BD D.∠ABC=∠ADC
10.如图,在中,下列结论错误的是( )
A. B. C. D.
二、填空题
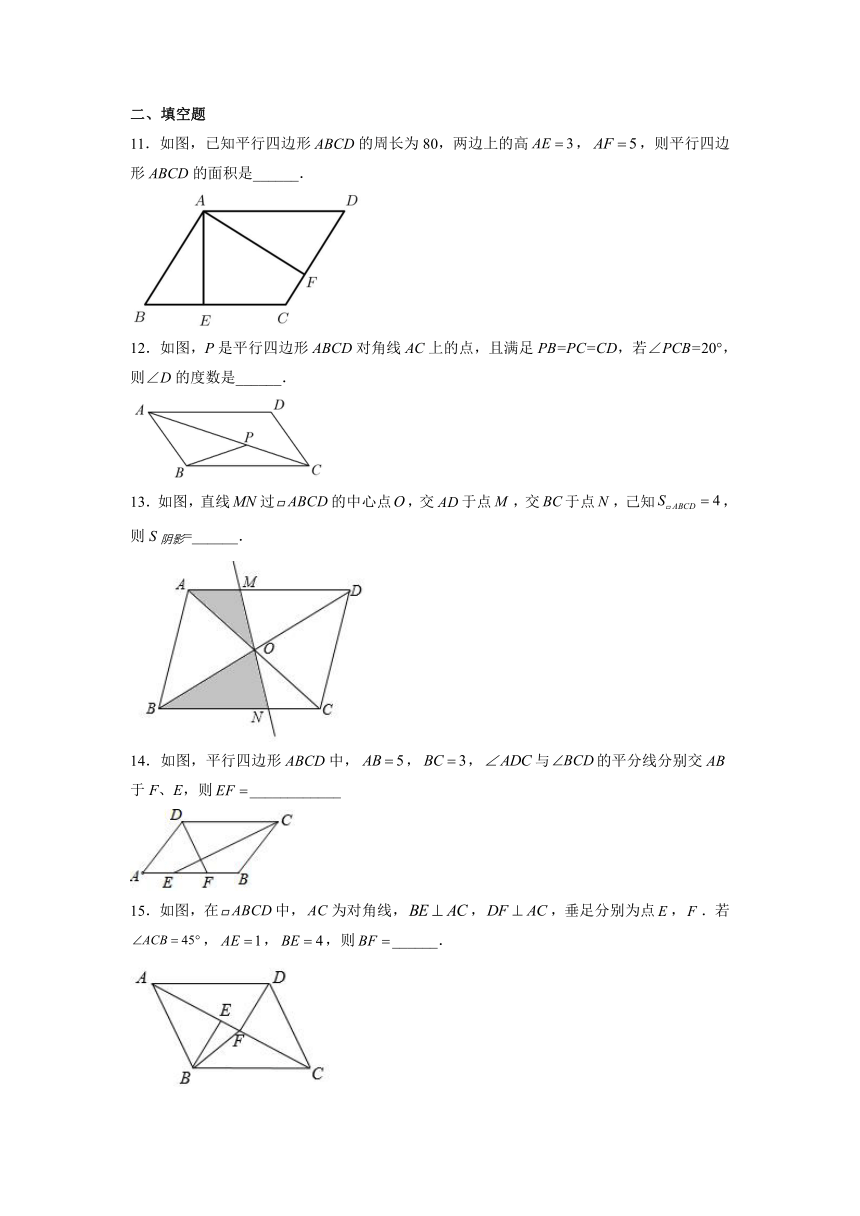
11.如图,已知平行四边形ABCD的周长为80,两边上的高,,则平行四边形ABCD的面积是______.
12.如图,P是平行四边形ABCD对角线AC上的点,且满足PB=PC=CD,若∠PCB=20°,则∠D的度数是______.
13.如图,直线过的中心点,交于点,交于点,己知,则S阴影=______.
14.如图,平行四边形ABCD中,,,与的平分线分别交AB于F、E,则____________
15.如图,在中,为对角线,,,垂足分别为点,.若,,,则______.
三、解答题
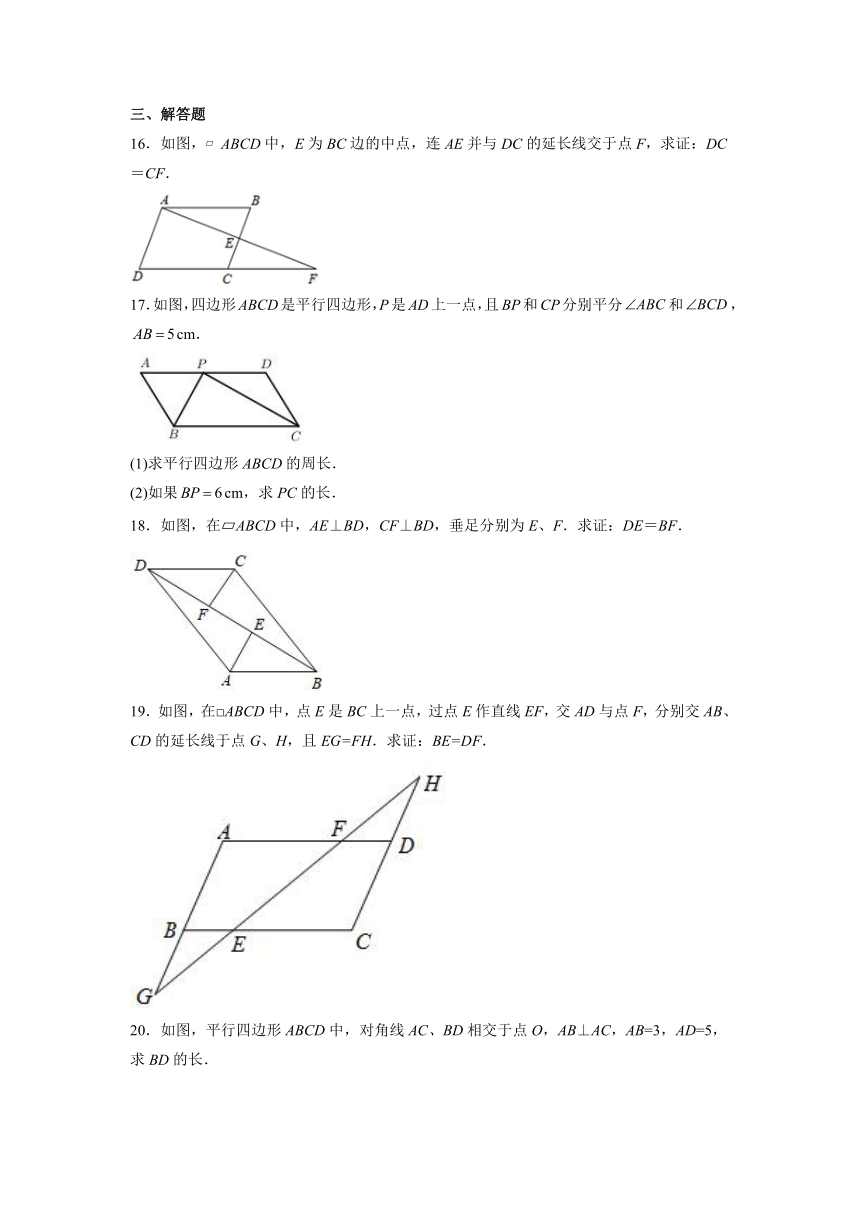
16.如图, ABCD中,E为BC边的中点,连AE并与DC的延长线交于点F,求证:DC=CF.
17.如图,四边形ABCD是平行四边形,P是AD上一点,且BP和CP分别平分和,cm.
(1)求平行四边形ABCD的周长.
(2)如果cm,求PC的长.
18.如图,在 ABCD中,AE⊥BD,CF⊥BD,垂足分别为E、F.求证:DE=BF.
19.如图,在□ABCD中,点E是BC上一点,过点E作直线EF,交AD与点F,分别交AB、CD的延长线于点G、H,且EG=FH.求证:BE=DF.
20.如图,平行四边形ABCD中,对角线AC、BD相交于点O,AB⊥AC,AB=3,AD=5,求BD的长.
21.如图,在中,对角线与相交于点O,.求的长度及的面积.
22.如图,在中,,求和的度数.
23.如图,在□ABCD中,点O是对角线AC、BD的交点,EF过点O且垂直于AD.
(1)求证:OE=OF;
(2)若S ABCD=63,OE=3.5,求AD的长.
【参考答案】
1.B 2.C 3.B 4.D 5.D 6.C 7.C 8.A 9.C 10.D
11.75
12.
13.1
14.1.
15.5
16.证明:∵四边形ABCD是平行四边形,
∴AB∥DC,AB=DC,
∴∠BAE=∠CFE,
∵点E是BC的中点,
∴BE=CE,
在△ABE和△FEC,
,
∴△ABE≌△FCE(AAS),
∴AB=FC,
∴DC=CF.
17.(1)解:∵BP、CP平分,,
∴,,
∵,
∴,,
∴,,
∴cm,(cm),
∴(cm),
∴平行四边形的周长为:(cm);
(2)解:由(1)可得,,
∵,
∴,
∴,
∴,
∴在中,cm,
∴(cm).
18.∵四边形ABCD是平行四边形,
∴AD=CB,,
∴∠ADE=∠CBF,
∵AE⊥BD,CF⊥BD,
∴∠AED=∠CFB=90°,
在△ADE和△CBF中,
,
∴△ADE≌△CBF(AAS),
∴DE=BF.
19.解:∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,
∴∠G=∠H,∠HFD=∠FEC,
又∵∠FEC=∠BEG,
∴∠HFD=∠GEB,
在△BGE和△DHF中,
∴△BGE≌△DHF(ASA)
∴BE=DF.
20.解:四边形是平行四边形
AB⊥AC,
在中,
在中,
21.解:∵BD⊥AD,AB=10,AD=8,
∴BD==6.
∵四边形ABCD是平行四边形,
∴OB=BD=3,
∴S ABCD=6×8=48.
故OB的长为3, ABCD的面积为48.
22.解:∵四边形ABCD是平行四边形,∠ADC=125°,
∴AD//CB,AB∥CD,∠B=∠ADC=125°,
∴∠ACB=∠CAD,
∵∠CAD=21°,
∴∠ACB=21°,
在△ABC中,∠CAB=180°-∠B-∠ACB=180°-125°-21°=34°,
23.(1)解:∵四边形ABCD是平行四边形,O是AC与BD的交点,
∴AO=CO,AD∥BC,
∴∠OAE=∠OCF,∠OEA=∠OFC,
∴△AOE≌△COF(AAS),
∴OE=OF;
(2)解:由(1)得OE=OF=3.5,
∴EF=7,
∵AD∥BC,EF⊥AD,
∴EF的长即为平行四边形ABCD中AD边上的高,
∵四边形ABCD的面积为63,
∴,
∴AD=9.
18.1.1 平行四边形的性质 课后练习
一、选择题
1.在 ABCD中,对角线AC与BD相交于点O,△BOC的周长为20cm,BC=12cm,则AC+BD的长是( )
A.8cm B.16cm C.24cm D.32cm
2.平行四边形的两条对角线将此平行四边形分成全等三角形的对数是( ).
A.2对 B.3对 C.4对 D.5对
3.在平行四边形ABCD中,AE⊥BC于E,AF⊥CD于F,AE=4,AF=6,平行四边形ABCD的周长为40,则平行四边形ABCD的面积是( )
A.36 B.48 C.40 D.24
4.如图,在平行四边形OABC中,对角线相交于点E,OA边在x轴上,点O为坐标原点,已知点,,则点C的坐标为( )
A. B. C. D.
5.如图,将平行四边形ABCD沿对角线AC折叠,使点B落在点处,若,为( )
A.36° B.144° C.108° D.126°
6.如图,在 ABCD中,对角线AC、BD相交于点O,过点O作OE⊥AC,交AD于点E,连接CE,若△CDE的周长为8,则 ABCD的周长为( )
A.8 B.10 C.16 D.20
7.如图所示,四边形ABCD是平行四边形,点E在线段BC的延长线上,若∠DCE=128°,则∠A=( )
A.32° B.42° C.52° D.62°
8.如图,的对角线、相交于点,则下列结论一定成立的是( )
A. B.
C. D.
9.如图,在 ABCD中,下列结论不一定成立的是( )
A.AB=CD B.∠1=∠2 C.AC⊥BD D.∠ABC=∠ADC
10.如图,在中,下列结论错误的是( )
A. B. C. D.
二、填空题
11.如图,已知平行四边形ABCD的周长为80,两边上的高,,则平行四边形ABCD的面积是______.
12.如图,P是平行四边形ABCD对角线AC上的点,且满足PB=PC=CD,若∠PCB=20°,则∠D的度数是______.
13.如图,直线过的中心点,交于点,交于点,己知,则S阴影=______.
14.如图,平行四边形ABCD中,,,与的平分线分别交AB于F、E,则____________
15.如图,在中,为对角线,,,垂足分别为点,.若,,,则______.
三、解答题
16.如图, ABCD中,E为BC边的中点,连AE并与DC的延长线交于点F,求证:DC=CF.
17.如图,四边形ABCD是平行四边形,P是AD上一点,且BP和CP分别平分和,cm.
(1)求平行四边形ABCD的周长.
(2)如果cm,求PC的长.
18.如图,在 ABCD中,AE⊥BD,CF⊥BD,垂足分别为E、F.求证:DE=BF.
19.如图,在□ABCD中,点E是BC上一点,过点E作直线EF,交AD与点F,分别交AB、CD的延长线于点G、H,且EG=FH.求证:BE=DF.
20.如图,平行四边形ABCD中,对角线AC、BD相交于点O,AB⊥AC,AB=3,AD=5,求BD的长.
21.如图,在中,对角线与相交于点O,.求的长度及的面积.
22.如图,在中,,求和的度数.
23.如图,在□ABCD中,点O是对角线AC、BD的交点,EF过点O且垂直于AD.
(1)求证:OE=OF;
(2)若S ABCD=63,OE=3.5,求AD的长.
【参考答案】
1.B 2.C 3.B 4.D 5.D 6.C 7.C 8.A 9.C 10.D
11.75
12.
13.1
14.1.
15.5
16.证明:∵四边形ABCD是平行四边形,
∴AB∥DC,AB=DC,
∴∠BAE=∠CFE,
∵点E是BC的中点,
∴BE=CE,
在△ABE和△FEC,
,
∴△ABE≌△FCE(AAS),
∴AB=FC,
∴DC=CF.
17.(1)解:∵BP、CP平分,,
∴,,
∵,
∴,,
∴,,
∴cm,(cm),
∴(cm),
∴平行四边形的周长为:(cm);
(2)解:由(1)可得,,
∵,
∴,
∴,
∴,
∴在中,cm,
∴(cm).
18.∵四边形ABCD是平行四边形,
∴AD=CB,,
∴∠ADE=∠CBF,
∵AE⊥BD,CF⊥BD,
∴∠AED=∠CFB=90°,
在△ADE和△CBF中,
,
∴△ADE≌△CBF(AAS),
∴DE=BF.
19.解:∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,
∴∠G=∠H,∠HFD=∠FEC,
又∵∠FEC=∠BEG,
∴∠HFD=∠GEB,
在△BGE和△DHF中,
∴△BGE≌△DHF(ASA)
∴BE=DF.
20.解:四边形是平行四边形
AB⊥AC,
在中,
在中,
21.解:∵BD⊥AD,AB=10,AD=8,
∴BD==6.
∵四边形ABCD是平行四边形,
∴OB=BD=3,
∴S ABCD=6×8=48.
故OB的长为3, ABCD的面积为48.
22.解:∵四边形ABCD是平行四边形,∠ADC=125°,
∴AD//CB,AB∥CD,∠B=∠ADC=125°,
∴∠ACB=∠CAD,
∵∠CAD=21°,
∴∠ACB=21°,
在△ABC中,∠CAB=180°-∠B-∠ACB=180°-125°-21°=34°,
23.(1)解:∵四边形ABCD是平行四边形,O是AC与BD的交点,
∴AO=CO,AD∥BC,
∴∠OAE=∠OCF,∠OEA=∠OFC,
∴△AOE≌△COF(AAS),
∴OE=OF;
(2)解:由(1)得OE=OF=3.5,
∴EF=7,
∵AD∥BC,EF⊥AD,
∴EF的长即为平行四边形ABCD中AD边上的高,
∵四边形ABCD的面积为63,
∴,
∴AD=9.
