2021-2022学年人教版九年级下册数学27.2.1相似三角形的判定巩固练习(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版九年级下册数学27.2.1相似三角形的判定巩固练习(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 656.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-21 14:52:32 | ||
图片预览



文档简介
2021-2022学年九年级下册数学巩固练习(人教版)
27.2.1相似三角形的判定
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,直线,直线AC和DF被,,所截,,,,则DE的长为( )
A.2 B.3 C.4 D.
2.如图,已知,,那么下列结论正确的是( )
A. B. C. D.
3.已知在中,点D为AB上一点,过点D作BC的平行线交AC于点E,过点E作AB的平行线交BC于点F.则下列说法不正确的是( )
A. B. C. D.
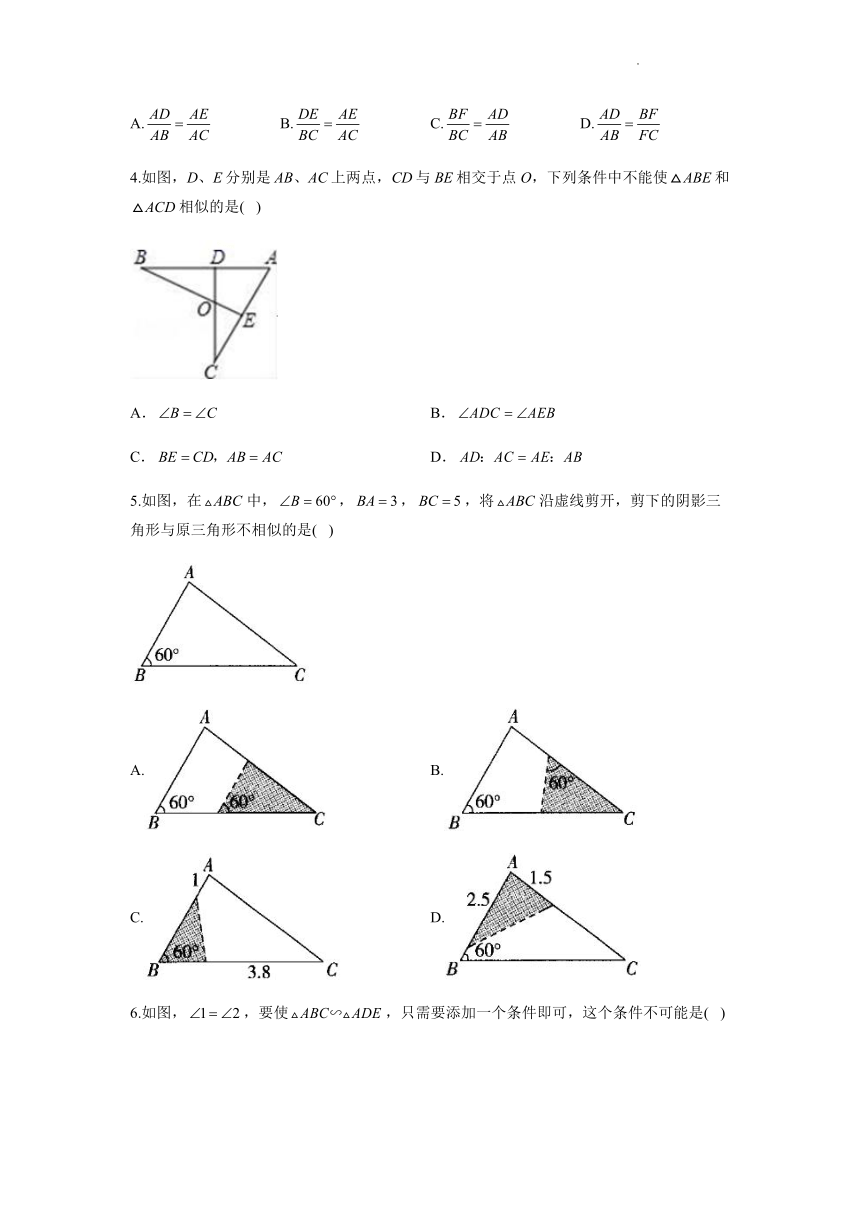
4.如图,D、E分别是AB、AC上两点,CD与BE相交于点O,下列条件中不能使和相似的是( )
A. B.
C. D.
5.如图,在中,,,,将沿虚线剪开,剪下的阴影三角形与原三角形不相似的是( )
A. B.
C. D.
6.如图,,要使,只需要添加一个条件即可,这个条件不可能是( )
A. B. C. D.
7.如图,在中,E、F分别是AB、AD的中点,EF交AC于点G,则的值是( )
A. B. C. D.
8.如图,点E是的边AD上的一点,且,连接BE并延长交CD的延长线于点F,若,,则的周长为( )
A.21 B.28 C.34 D.42
9.如图,,点E在AB上,点F在CD上,AC、BD、EF相交于点O,则图中相似三角形共有( )
A.1对 B.2对 C.3对 D.4对
10.如图,中,,于点M,于点N,BM,CN交于点O,连接MN.下列结论:
①;
②图中共有8对相似三角形;
③.
其中正确的个数是( )
A.1 B.2 C.3 D.0
二、填空题
11.如图,,,,分别是和的中点,则的长度是_____.
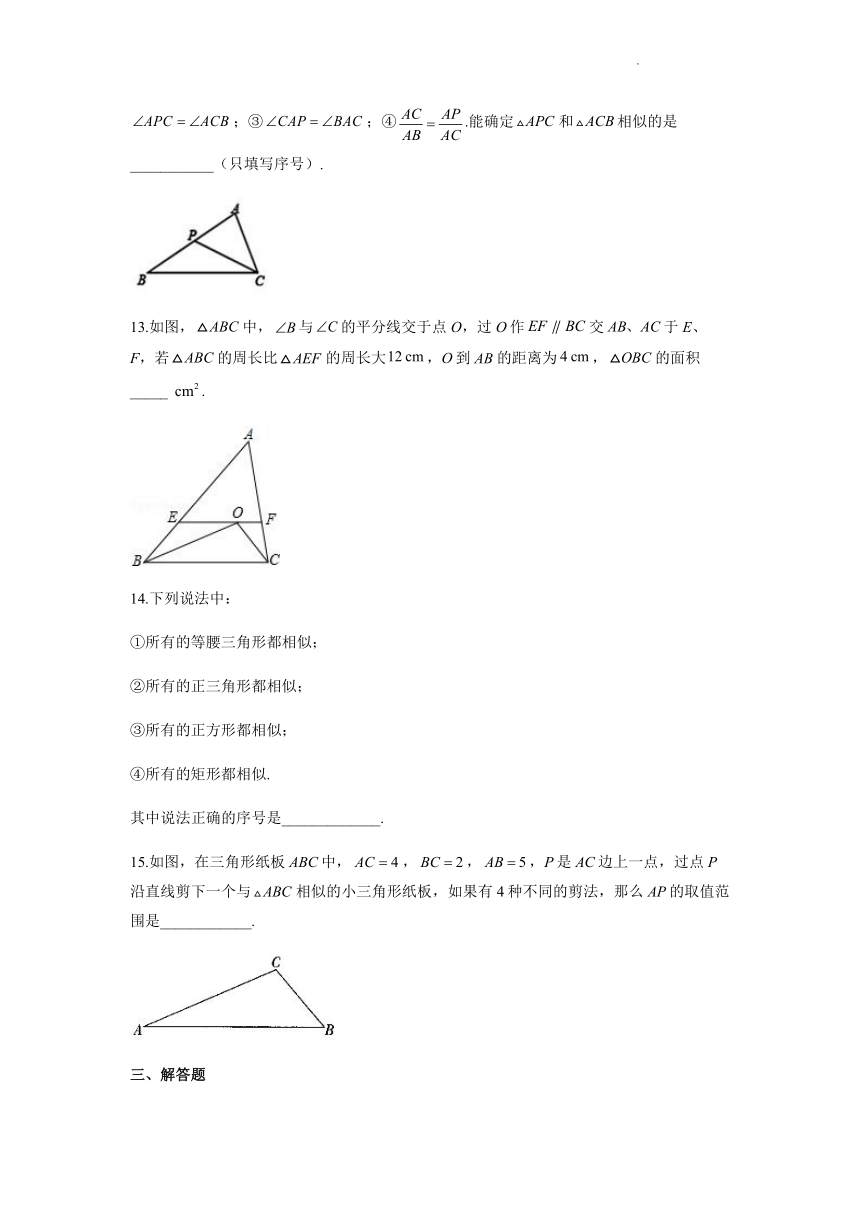
12.如图,中,P为AB上点,在下列四个条件中:①;②;③;④.能确定和相似的是___________(只填写序号).
13.如图,中,与的平分线交于点O,过O作交于E、F,若的周长比的周长大,O到的距离为,的面积_____.
14.下列说法中:
①所有的等腰三角形都相似;
②所有的正三角形都相似;
③所有的正方形都相似;
④所有的矩形都相似.
其中说法正确的序号是_____________.
15.如图,在三角形纸板ABC中,,,,P是AC边上一点,过点P沿直线剪下一个与相似的小三角形纸板,如果有4种不同的剪法,那么AP的取值范围是____________.
三、解答题
16.如图,已知,它们依次交直线于点和.若,,
(1)求的长.
(2)如果,求的长.
17.根据下列条件,判断与是否相似,并说明理由.
(1),,,,,;
(2),,,,,.
18.如图,在中,,,.在中,,,.求证:.
19.如图,点B,C分别在的边AD,AE上,且,,,.求证:.
20.如图,在和中,D、分别是AB、上一点,.
(1)当时,求证:.
证明的途径可以用如图所示的框图表示,请填写其中的空格.
(2)当时,判断与是否相似,并说明理由.
参考答案
1.答案:D
解析:直线,,,,,,,故选D.
2.答案:A
解析:,,即,,.故选A.
3.答案:D
解析:
4.答案:C
解析:
5.答案:D
解析:A项和B项,阴影部分的三角形与原三角形有两个角相等,则两三角形相似,故A、B不符合题意;C项,,两三角形中两条边成比例且夹角相等,则两三角形相似,故C不符合题意.故选D.
6.答案:D
解析:,,.选项A,添加,利用“两角定理”可得,故A不合题意;选项B,添加,利用“两角定理”可得,故B不合题意;选项C,添加(即),利用“两边夹角定理”可得,故C不合题意;选项D,添加,不能证明,故D符合题意.故选D.
7.答案:A
解析:如图,连接BD,与AC交于O,点E、F分别是AB、AD的中点,EF是的中位线,,,,,又,.故选A.
8.答案:C
解析:四边形ABCD是平行四边形,,,.,,,,,的周长.故选C.
9.答案:C
解析:,,,.故选C.
10.答案:C
解析:,,,又,,,即,又,,,故①正确;易得,,,图中共有8对相似三角形,故②正确;中,,,,,,即,故③正确.故选C.
11.答案:1
解析:
12.答案:①②③
解析:
13.答案: .
解析:
14.答案:②③
解析:①所有的等腰三角形都相似,错误;
②所有的正三角形都相似,正确;
③所有的正方形都相似,正确;
④所有的矩形都相似,错误.
故答案为:②③.
15.答案:
解析:如图,①过点P作交BC于点G,作交AB于点E,则,,此时点P在线段AC上,且不能与点A和点C重合,故;②过点P作,交AB于点D,则,此时P点在线段AC上,且不能与点A重合,故;③过点P作交BC于F点,因为,所以,因为当F与B重合时,AP取得最小值,,所以此时,所以,解得,所以,又P不能与点C重合,故.综上所述,所求AP的取值范围为.
16.答案:(1)
即
又∵,即
∴
(2)过A作交BE于H,交CF于G
∵
∴
又∵
又∵
故
解析:
17.答案:(1).
理由:,,,
.
(2).
理由:,,,
.
解析:
18.答案:证明:在中,
,,,
,
.
在和中,
,
.
解析:
19.答案:证明:,,,.
,,
,.
,
又,
.
解析:
20.答案:(1);.
(2).理由:如图,分别过点D,作,,DE交AC于点E,交于点.
,
,
.
同理,.
,
,
.
同理,.
,即,
.
,
.
,
.
,
.
同理,,
.
,
.
解析:
27.2.1相似三角形的判定
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,直线,直线AC和DF被,,所截,,,,则DE的长为( )
A.2 B.3 C.4 D.
2.如图,已知,,那么下列结论正确的是( )
A. B. C. D.
3.已知在中,点D为AB上一点,过点D作BC的平行线交AC于点E,过点E作AB的平行线交BC于点F.则下列说法不正确的是( )
A. B. C. D.
4.如图,D、E分别是AB、AC上两点,CD与BE相交于点O,下列条件中不能使和相似的是( )
A. B.
C. D.
5.如图,在中,,,,将沿虚线剪开,剪下的阴影三角形与原三角形不相似的是( )
A. B.
C. D.
6.如图,,要使,只需要添加一个条件即可,这个条件不可能是( )
A. B. C. D.
7.如图,在中,E、F分别是AB、AD的中点,EF交AC于点G,则的值是( )
A. B. C. D.
8.如图,点E是的边AD上的一点,且,连接BE并延长交CD的延长线于点F,若,,则的周长为( )
A.21 B.28 C.34 D.42
9.如图,,点E在AB上,点F在CD上,AC、BD、EF相交于点O,则图中相似三角形共有( )
A.1对 B.2对 C.3对 D.4对
10.如图,中,,于点M,于点N,BM,CN交于点O,连接MN.下列结论:
①;
②图中共有8对相似三角形;
③.
其中正确的个数是( )
A.1 B.2 C.3 D.0
二、填空题
11.如图,,,,分别是和的中点,则的长度是_____.
12.如图,中,P为AB上点,在下列四个条件中:①;②;③;④.能确定和相似的是___________(只填写序号).
13.如图,中,与的平分线交于点O,过O作交于E、F,若的周长比的周长大,O到的距离为,的面积_____.
14.下列说法中:
①所有的等腰三角形都相似;
②所有的正三角形都相似;
③所有的正方形都相似;
④所有的矩形都相似.
其中说法正确的序号是_____________.
15.如图,在三角形纸板ABC中,,,,P是AC边上一点,过点P沿直线剪下一个与相似的小三角形纸板,如果有4种不同的剪法,那么AP的取值范围是____________.
三、解答题
16.如图,已知,它们依次交直线于点和.若,,
(1)求的长.
(2)如果,求的长.
17.根据下列条件,判断与是否相似,并说明理由.
(1),,,,,;
(2),,,,,.
18.如图,在中,,,.在中,,,.求证:.
19.如图,点B,C分别在的边AD,AE上,且,,,.求证:.
20.如图,在和中,D、分别是AB、上一点,.
(1)当时,求证:.
证明的途径可以用如图所示的框图表示,请填写其中的空格.
(2)当时,判断与是否相似,并说明理由.
参考答案
1.答案:D
解析:直线,,,,,,,故选D.
2.答案:A
解析:,,即,,.故选A.
3.答案:D
解析:
4.答案:C
解析:
5.答案:D
解析:A项和B项,阴影部分的三角形与原三角形有两个角相等,则两三角形相似,故A、B不符合题意;C项,,两三角形中两条边成比例且夹角相等,则两三角形相似,故C不符合题意.故选D.
6.答案:D
解析:,,.选项A,添加,利用“两角定理”可得,故A不合题意;选项B,添加,利用“两角定理”可得,故B不合题意;选项C,添加(即),利用“两边夹角定理”可得,故C不合题意;选项D,添加,不能证明,故D符合题意.故选D.
7.答案:A
解析:如图,连接BD,与AC交于O,点E、F分别是AB、AD的中点,EF是的中位线,,,,,又,.故选A.
8.答案:C
解析:四边形ABCD是平行四边形,,,.,,,,,的周长.故选C.
9.答案:C
解析:,,,.故选C.
10.答案:C
解析:,,,又,,,即,又,,,故①正确;易得,,,图中共有8对相似三角形,故②正确;中,,,,,,即,故③正确.故选C.
11.答案:1
解析:
12.答案:①②③
解析:
13.答案: .
解析:
14.答案:②③
解析:①所有的等腰三角形都相似,错误;
②所有的正三角形都相似,正确;
③所有的正方形都相似,正确;
④所有的矩形都相似,错误.
故答案为:②③.
15.答案:
解析:如图,①过点P作交BC于点G,作交AB于点E,则,,此时点P在线段AC上,且不能与点A和点C重合,故;②过点P作,交AB于点D,则,此时P点在线段AC上,且不能与点A重合,故;③过点P作交BC于F点,因为,所以,因为当F与B重合时,AP取得最小值,,所以此时,所以,解得,所以,又P不能与点C重合,故.综上所述,所求AP的取值范围为.
16.答案:(1)
即
又∵,即
∴
(2)过A作交BE于H,交CF于G
∵
∴
又∵
又∵
故
解析:
17.答案:(1).
理由:,,,
.
(2).
理由:,,,
.
解析:
18.答案:证明:在中,
,,,
,
.
在和中,
,
.
解析:
19.答案:证明:,,,.
,,
,.
,
又,
.
解析:
20.答案:(1);.
(2).理由:如图,分别过点D,作,,DE交AC于点E,交于点.
,
,
.
同理,.
,
,
.
同理,.
,即,
.
,
.
,
.
,
.
同理,,
.
,
.
解析:
