苏科版七年级数学下册 第9章 数学活动 拼图公式教案
文档属性
| 名称 | 苏科版七年级数学下册 第9章 数学活动 拼图公式教案 |  | |
| 格式 | docx | ||
| 文件大小 | 44.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-21 17:12:09 | ||
图片预览

文档简介
数学活动—拼图·公式
教学目标:
(1)通过拼图与公式的联系加强学生学习数学的兴趣,进一步熟悉整式乘法和因式分解;
(2)获得一些研究问题的方法和经验,加深对知识的理解,体会数形结合思想.
教学重点:通过拼图活动巩固整式乘法和因式分解的有关知识.
教学难点:从具体问题到建立数学模型,通过拼图活动探究一些二次三项式的因式分解.
教学过程:
情境引入:“数缺形时少直观,形少数时难入微;
数形结合百般好,隔离分家万事休.” ——华罗庚
情境(一):王大爷准备把长为a米,宽为b米的这块地向外扩建,使得长再增加c米,则扩建后地的面积为:
发现等式 : 。
情境(二):王大爷在刚才扩建的基础上再向外扩建,使得宽再增加d米,则扩建后地的面积为:
发现等式 : 。
变形1:如果王大爷这块地是边长为x米的正方形向外扩建时,使长增加a米,宽增加b米,则扩建后的面积为:
发现等式 : 。
口算: (x+5)(x+2) =
(x-3)(x+1) =
变形2: 如果王大爷将这块边长为a米的正方形地向外扩建后时,长和宽都增加b米,则扩建后的面积为:
发现等式 : 。
思考:
1.以上图形的面积主要有几种算法
2.以上图形的面积验证了哪些公式?
3.你还有其它的见解吗?
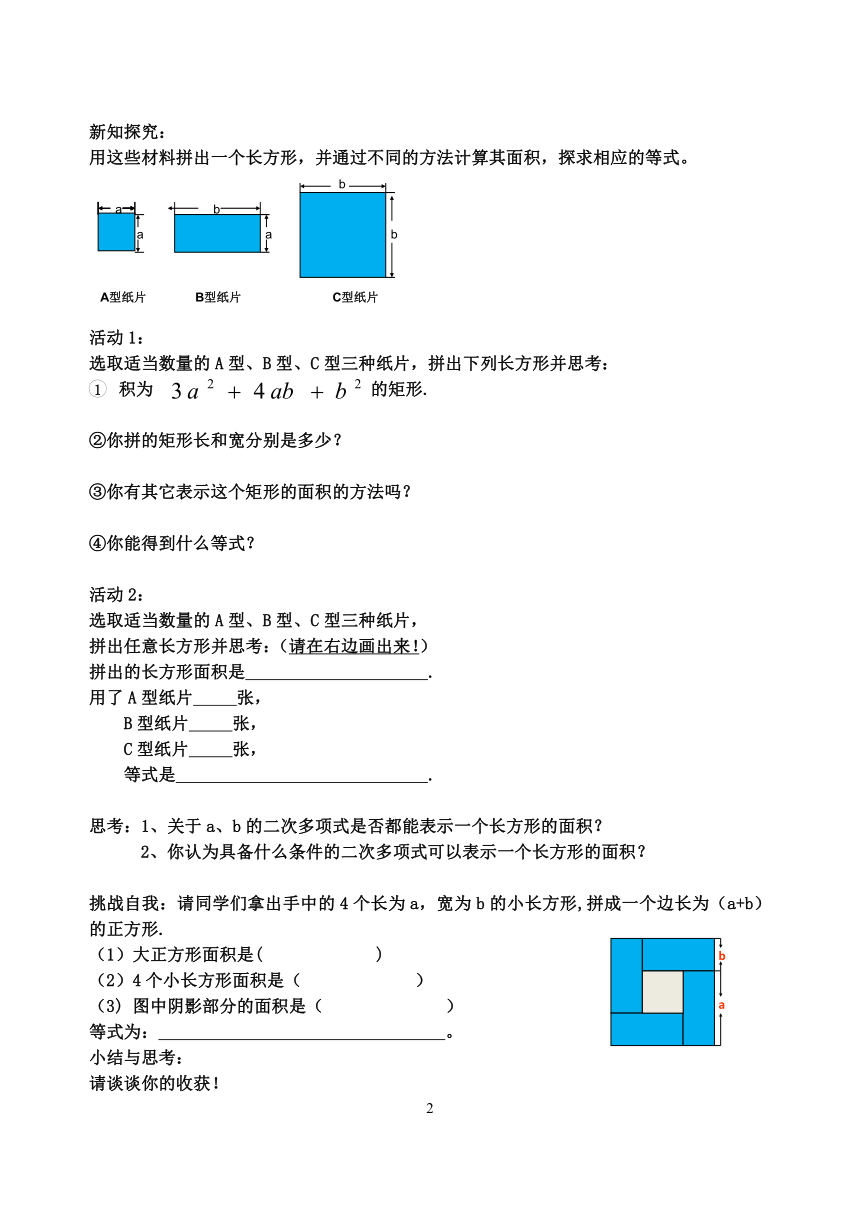
新知探究:
用这些材料拼出一个长方形,并通过不同的方法计算其面积,探求相应的等式。
活动1:
选取适当数量的A型、B型、C型三种纸片,拼出下列长方形并思考:
积为 的矩形.
②你拼的矩形长和宽分别是多少?
③你有其它表示这个矩形的面积的方法吗?
④你能得到什么等式?
活动2:
选取适当数量的A型、B型、C型三种纸片,
拼出任意长方形并思考:(请在右边画出来!)
拼出的长方形面积是 .
用了A型纸片 张,
B型纸片 张,
C型纸片 张,
等式是 .
思考:1、关于a、b的二次多项式是否都能表示一个长方形的面积?
2、你认为具备什么条件的二次多项式可以表示一个长方形的面积?
挑战自我:请同学们拿出手中的4个长为a,宽为b的小长方形,拼成一个边长为(a+b)的正方形.
(1)大正方形面积是( )
(2)4个小长方形面积是( )
(3) 图中阴影部分的面积是( )
等式为: 。
小结与思考:
请谈谈你的收获!
课后作业:
1.把几个图形拼成一个新的图形,再通过图形面积的计算,常常可以得
到一些有用的式子。美国第二十任总统伽菲尔德就由这个图,由两个
边长分别为a、b、c的直角三角形和一个两条直角边都是c的直角三
角形拼成一个新的图形,如图所示,试用不同的方法计算这个图形的
面积,你能发现会什么?
2.如图①是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四个相同的小长方形,然后按图②的方式拼成一个正方形.
图① 图② 图③
(1)你认为图②中的阴影部分的正方形的边长等于________;
(2)请用两种不同的方法列代数式表示图②中阴影部分的面积.
方法①: ;方法②: ;
(3)请你观察图②,利用图形的面积写出 、 ,这三个代数式之间的等量关系: ;
(4)根据(3)中的结论,若,,则 ;
(5)有许多代数恒等式可以用图形的面积来表示.
如图③,它表示了 .
试画出一个几何图形,使它的面积能表示:
3、活动材料:若干块如图所示的长方形和正方形硬纸片。
活动要求:用若干块这样的长方形和正方形硬纸片拼成一个新的长方形,通过不同的方法计算面积,探求相应的等式。
你能用材料,利用拼图的方法将a2+3ab+2b2分解因式吗?请画出图形。
你能用材料,利用拼图的方法将a2+4ab+3b2分解因式吗?请画出图形。
4、有许多个边长为a的小正方形、边长为b的大正方形,以及长为b宽为a的长方形,取其中的若干个(三种图形都要取到)拼成一个长方形使其面积为a2+5ab+nb2(n是正整数)
(1) n的可能数值有 ,画出其中的一个图形。
(2) 根据所画图形可将多项式a2+5ab+ b2 分解因式 (两种情况)
2
教学目标:
(1)通过拼图与公式的联系加强学生学习数学的兴趣,进一步熟悉整式乘法和因式分解;
(2)获得一些研究问题的方法和经验,加深对知识的理解,体会数形结合思想.
教学重点:通过拼图活动巩固整式乘法和因式分解的有关知识.
教学难点:从具体问题到建立数学模型,通过拼图活动探究一些二次三项式的因式分解.
教学过程:
情境引入:“数缺形时少直观,形少数时难入微;
数形结合百般好,隔离分家万事休.” ——华罗庚
情境(一):王大爷准备把长为a米,宽为b米的这块地向外扩建,使得长再增加c米,则扩建后地的面积为:
发现等式 : 。
情境(二):王大爷在刚才扩建的基础上再向外扩建,使得宽再增加d米,则扩建后地的面积为:
发现等式 : 。
变形1:如果王大爷这块地是边长为x米的正方形向外扩建时,使长增加a米,宽增加b米,则扩建后的面积为:
发现等式 : 。
口算: (x+5)(x+2) =
(x-3)(x+1) =
变形2: 如果王大爷将这块边长为a米的正方形地向外扩建后时,长和宽都增加b米,则扩建后的面积为:
发现等式 : 。
思考:
1.以上图形的面积主要有几种算法
2.以上图形的面积验证了哪些公式?
3.你还有其它的见解吗?
新知探究:
用这些材料拼出一个长方形,并通过不同的方法计算其面积,探求相应的等式。
活动1:
选取适当数量的A型、B型、C型三种纸片,拼出下列长方形并思考:
积为 的矩形.
②你拼的矩形长和宽分别是多少?
③你有其它表示这个矩形的面积的方法吗?
④你能得到什么等式?
活动2:
选取适当数量的A型、B型、C型三种纸片,
拼出任意长方形并思考:(请在右边画出来!)
拼出的长方形面积是 .
用了A型纸片 张,
B型纸片 张,
C型纸片 张,
等式是 .
思考:1、关于a、b的二次多项式是否都能表示一个长方形的面积?
2、你认为具备什么条件的二次多项式可以表示一个长方形的面积?
挑战自我:请同学们拿出手中的4个长为a,宽为b的小长方形,拼成一个边长为(a+b)的正方形.
(1)大正方形面积是( )
(2)4个小长方形面积是( )
(3) 图中阴影部分的面积是( )
等式为: 。
小结与思考:
请谈谈你的收获!
课后作业:
1.把几个图形拼成一个新的图形,再通过图形面积的计算,常常可以得
到一些有用的式子。美国第二十任总统伽菲尔德就由这个图,由两个
边长分别为a、b、c的直角三角形和一个两条直角边都是c的直角三
角形拼成一个新的图形,如图所示,试用不同的方法计算这个图形的
面积,你能发现会什么?
2.如图①是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四个相同的小长方形,然后按图②的方式拼成一个正方形.
图① 图② 图③
(1)你认为图②中的阴影部分的正方形的边长等于________;
(2)请用两种不同的方法列代数式表示图②中阴影部分的面积.
方法①: ;方法②: ;
(3)请你观察图②,利用图形的面积写出 、 ,这三个代数式之间的等量关系: ;
(4)根据(3)中的结论,若,,则 ;
(5)有许多代数恒等式可以用图形的面积来表示.
如图③,它表示了 .
试画出一个几何图形,使它的面积能表示:
3、活动材料:若干块如图所示的长方形和正方形硬纸片。
活动要求:用若干块这样的长方形和正方形硬纸片拼成一个新的长方形,通过不同的方法计算面积,探求相应的等式。
你能用材料,利用拼图的方法将a2+3ab+2b2分解因式吗?请画出图形。
你能用材料,利用拼图的方法将a2+4ab+3b2分解因式吗?请画出图形。
4、有许多个边长为a的小正方形、边长为b的大正方形,以及长为b宽为a的长方形,取其中的若干个(三种图形都要取到)拼成一个长方形使其面积为a2+5ab+nb2(n是正整数)
(1) n的可能数值有 ,画出其中的一个图形。
(2) 根据所画图形可将多项式a2+5ab+ b2 分解因式 (两种情况)
2
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
