六年级下册数学一课一练-1.2圆柱的表面积 北师大版(含答案)
文档属性
| 名称 | 六年级下册数学一课一练-1.2圆柱的表面积 北师大版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 62.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-21 17:13:47 | ||
图片预览


文档简介
六年级下册数学一课一练-1.2圆柱的表面积
一、单选题
1.把底面直径和高相等的圆柱的侧面展开可能是( )。
A. 正方形 B. 梯形 C. 长方形 D. 都有可能
2.长方形围绕一条边旋转一周得到了:( )
A. B. C.
3.如果圆柱的侧面展开图是一个正方形,这个圆柱的底面直径是5厘米,那么圆柱的高是( )厘米。
A. 5 B. 10 C. 15.7 D. 2.5
4.圆柱的侧面展开图是正方形,这个圆柱的底面直径和高的比是( )。
A. π:1 B. 1:1 C. 1:π
二、判断题
5.将圆柱的侧面沿高展开有可能是长方形,也有可能是正方形,还有可能是平行四边形。( )
6..用一张长20厘米,宽12厘米的长方形纸围一个圆柱,不管怎么样围,圆柱的侧面积都是240平方厘米.( )
7.一个圆柱底面周长是10米,高是1米,它的侧面积是31.4平方米。( )
8.一个圆柱的直径和高相等,则圆柱体的侧面展开图是正方形。( )
三、填空题
9.在一个体积是14.13ml且装满水的圆柱形容器里,放入一个等底等高的圆锥体后.容器里还有水________ ml.
10.计算下面圆柱的表面积和体积.
表面积:________
体积:________
11.一个圆柱的底面直径是4cm,高是15cm,它的表面积是________cm2 , 体积是________cm3。
四、解答题
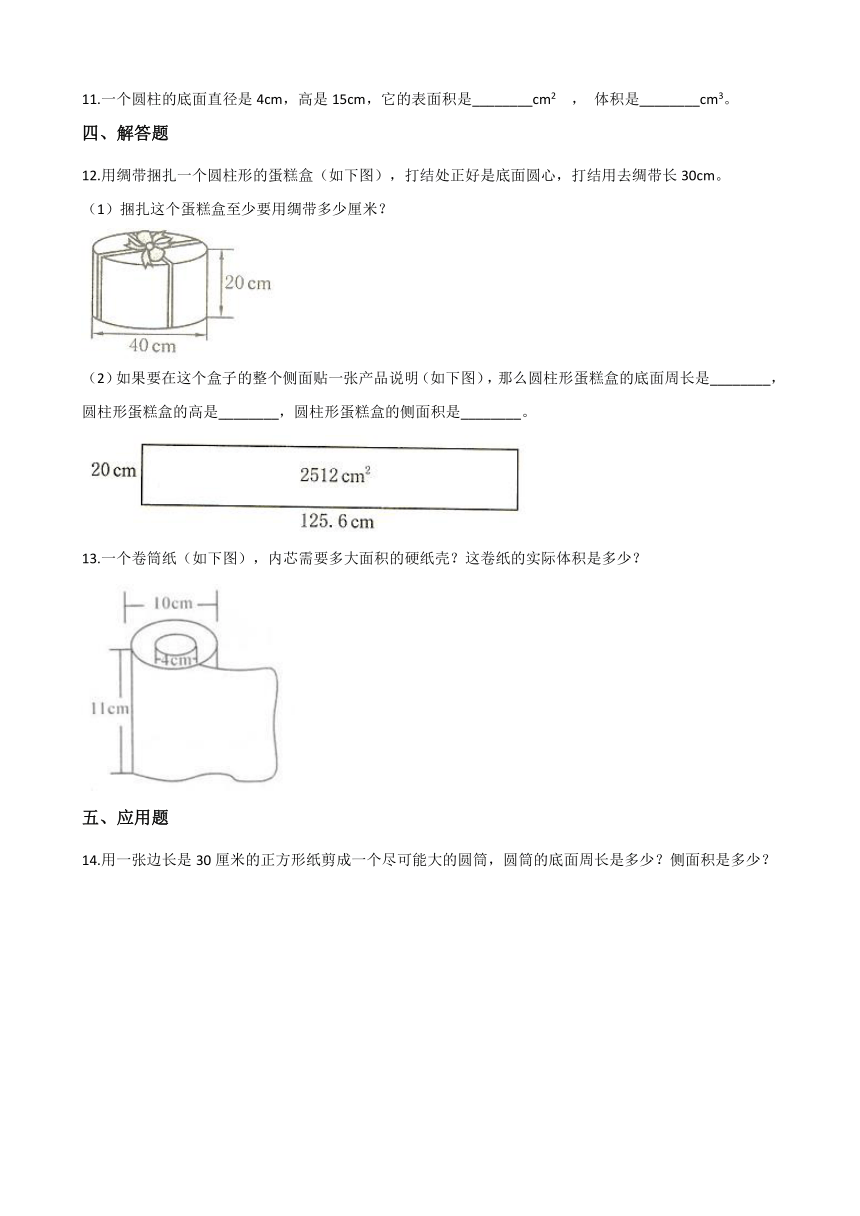
12.用绸带捆扎一个圆柱形的蛋糕盒(如下图),打结处正好是底面圆心,打结用去绸带长30cm。
(1)捆扎这个蛋糕盒至少要用绸带多少厘米?
(2)如果要在这个盒子的整个侧面贴一张产品说明(如下图),那么圆柱形蛋糕盒的底面周长是________,圆柱形蛋糕盒的高是________,圆柱形蛋糕盒的侧面积是________。
13.一个卷筒纸(如下图),内芯需要多大面积的硬纸壳?这卷纸的实际体积是多少?
五、应用题
14.用一张边长是30厘米的正方形纸剪成一个尽可能大的圆筒,圆筒的底面周长是多少?侧面积是多少?
参考答案
一、单选题
1.【答案】 C
【解析】【解答】把底面直径和高相等的圆柱的侧面展开可能是长方形.
故答案为:C.
【分析】圆柱的底面直径和高相等时,侧面展开是长方形,因为底面展开的长度是圆柱的底面周长而不是直径,所以周长不等于高,是长方形.
2.【答案】 A
【解析】围绕长方形的一条边旋转得到额圆柱体,围绕直角三角形一条直角边旋转得到了圆锥体,围绕半圆的直径宣战的到了球体,所以,我们选择答案为A。
3.【答案】 C
【解析】【解答】解:高是:3.14×5=15.7(厘米)
故答案为:C
【分析】圆柱的侧面展开后是一个长方形或正方形,长方形或正方形的一条边与底面周长相等,另一条边与高相等;当底面周长和高相等时侧面展开就是一个正方形.
4.【答案】 C
【解析】【解答】直径:高=d:=1:
故答案为:C
【分析】题意可知,圆柱侧面展开图是正方形时,圆柱的底面周长等于圆柱的高。底面直径和高的比也就是底面直径和底面周长的比。
二、判断题
5.【答案】 错误
【解析】【解答】 将圆柱的侧面沿高展开有可能是长方形,也有可能是正方形,原题说法错误。
故答案为:错误。
【分析】 此题主要考查了圆柱的展开图,把一个圆柱沿高展开,当圆柱的底面周长等于圆柱的高时,展开图是正方形;当圆柱的底面周长不等于圆柱的高时,展开图是长方形;当把一个圆柱不是沿高剪开,而是斜着剪开,得到的图形是平行四边形,据此判断。
6.【答案】 正确
【解析】【解答】20×12=240(平方厘米),原题说法正确.
故答案为:正确.
【分析】根据题意可知,用一张长方形的纸围成一个圆柱,不管怎么围,圆柱的侧面积等于长方形的面积,长方形的面积=长×宽,据此解答.
7.【答案】 错误
【解析】【解答】解:10×1=10(平方米)
故答案为:错误。
【分析】根据题意可知圆柱的侧面积=底面周长×高。
8.【答案】 错误
【解析】【解答】当圆柱体的底面周长等于高时,侧面展开图是正方形,原题说法错误.
故答案为:错误.
【分析】如果圆柱体的侧面展开图是正方形,得到的正方形一条边是圆柱体的高,另一条边是圆柱体的底面周长,因为正方形的四条边相等,所以当圆柱体的侧面展开图是正方形,圆柱体的底面周长等于高,据此判断.
三、填空题
9.【答案】 9.42
【解析】【解答】:14.13
=14.13
=9.42(毫升)
【分析】:因为等底等高的圆锥体积是圆柱的, 所以在装满水圆柱形容器里,放入一个等底等高的圆锥体后,水会溢出和圆锥的体积相等的水,即溢出14.13毫升的, 由此可得容器内还剩下的水,由此即可解答。
10.【答案】 244.92平方分米;282.6立方分米
【解析】【解答】底面半径:
18.84÷3.14÷2
=6÷2
=3(dm)
表面积:
18.84×10+3.14×32×2
=18.84×10+3.14×9×2
=188.4+56.52
=244.92(平方分米)
体积:
3.14×32×10
=3.14×9×10
=28.26×10
=282.6(立方分米)
故答案为:244.92平方分米;282.6立方分米.
【分析】已知圆柱的底面周长和高,要求表面积和体积,先求出圆柱的底面半径,用公式:C÷π÷2=r,要求表面积,用公式:S=Ch+2πr2 , 要求体积,用公式:V=πr2h,据此列式解答.
11.【答案】 213.52;188.4
【解析】【解答】4÷2=2(cm);
圆柱的表面积:
3.14×4×15+3.14×22×2
=3.14×4×15+3.14×4×2
=12.56×15+12.56×2
=188.4+25.12
=213.52(cm2)
圆柱的体积:
3.14×22×15
=3.14×4×15
=12.56×15
=188.4(cm3)
故答案为:213.52;188.4 。
【分析】已知圆柱的底面直径和高,先求出圆柱的底面半径,用直径÷2=半径,要求圆柱的表面积,用公式:圆柱的表面积=圆柱的侧面积+底面积×2,据此列式解答;
要求圆柱的体积,用公式:圆柱的体积=底面积×高,据此列式解答.
四、解答题
12.【答案】 (1)解:40×4+20×4+30
=160+80+30
=240+30
=270(厘米)
答: 捆扎这个蛋糕盒至少要用绸带270厘米。
(2)125.6cm;20cm;2512cm2
【解析】【解答】(2) 如果要在这个盒子的整个侧面贴一张产品说明(如下图),那么圆柱形蛋糕盒的底面周长是125.6cm,圆柱形蛋糕盒的高是20cm,圆柱形蛋糕盒的侧面积是2512cm2。
【分析】(1)观察图可知, 捆扎这个蛋糕盒需要的绸带长度=底面直径×4+高×4+打结用去的绸带长度,据此列式解答;
(2)观察图可知,圆柱的侧面沿高展开,得到一共长方形,长方形的长是圆柱的底面周长,长方形的宽是圆柱的高,长方形的面积是圆柱的侧面积,据此解答。
13.【答案】 解:S=3.14×4×11=138.16(cm2)
V=3.14×(10÷2)2×11-3.14×(4÷2)2×11=725.34(cm3)
答:内芯需要138.16cm2的硬纸壳,这卷纸的实际体积是725.34cm3。
【解析】【分析】内芯需要硬纸壳的面积=卷纸内壁的侧面积=内芯的直径×π×h;
这卷纸的实际体积=这卷纸实心的体积-掏去的内芯的体积,其中这卷纸实心的体积=(整个卷纸的直径÷2)2×π×h,掏去的内芯的体积=(内芯的直径÷2)2×π×h。
五、应用题
14.【答案】解:圆筒的底面周长是30厘米
30×30=900(平方厘米)
答:圆筒的底面周长是30厘米;侧面积是900平方厘米。
【解析】【分析】根据圆柱的侧面展开图的特点,圆筒的底面周长是正方形的边长;正方形的面积正好是这个圆柱体的侧面积.利用正方形的面积公式即可解答。
一、单选题
1.把底面直径和高相等的圆柱的侧面展开可能是( )。
A. 正方形 B. 梯形 C. 长方形 D. 都有可能
2.长方形围绕一条边旋转一周得到了:( )
A. B. C.
3.如果圆柱的侧面展开图是一个正方形,这个圆柱的底面直径是5厘米,那么圆柱的高是( )厘米。
A. 5 B. 10 C. 15.7 D. 2.5
4.圆柱的侧面展开图是正方形,这个圆柱的底面直径和高的比是( )。
A. π:1 B. 1:1 C. 1:π
二、判断题
5.将圆柱的侧面沿高展开有可能是长方形,也有可能是正方形,还有可能是平行四边形。( )
6..用一张长20厘米,宽12厘米的长方形纸围一个圆柱,不管怎么样围,圆柱的侧面积都是240平方厘米.( )
7.一个圆柱底面周长是10米,高是1米,它的侧面积是31.4平方米。( )
8.一个圆柱的直径和高相等,则圆柱体的侧面展开图是正方形。( )
三、填空题
9.在一个体积是14.13ml且装满水的圆柱形容器里,放入一个等底等高的圆锥体后.容器里还有水________ ml.
10.计算下面圆柱的表面积和体积.
表面积:________
体积:________
11.一个圆柱的底面直径是4cm,高是15cm,它的表面积是________cm2 , 体积是________cm3。
四、解答题
12.用绸带捆扎一个圆柱形的蛋糕盒(如下图),打结处正好是底面圆心,打结用去绸带长30cm。
(1)捆扎这个蛋糕盒至少要用绸带多少厘米?
(2)如果要在这个盒子的整个侧面贴一张产品说明(如下图),那么圆柱形蛋糕盒的底面周长是________,圆柱形蛋糕盒的高是________,圆柱形蛋糕盒的侧面积是________。
13.一个卷筒纸(如下图),内芯需要多大面积的硬纸壳?这卷纸的实际体积是多少?
五、应用题
14.用一张边长是30厘米的正方形纸剪成一个尽可能大的圆筒,圆筒的底面周长是多少?侧面积是多少?
参考答案
一、单选题
1.【答案】 C
【解析】【解答】把底面直径和高相等的圆柱的侧面展开可能是长方形.
故答案为:C.
【分析】圆柱的底面直径和高相等时,侧面展开是长方形,因为底面展开的长度是圆柱的底面周长而不是直径,所以周长不等于高,是长方形.
2.【答案】 A
【解析】围绕长方形的一条边旋转得到额圆柱体,围绕直角三角形一条直角边旋转得到了圆锥体,围绕半圆的直径宣战的到了球体,所以,我们选择答案为A。
3.【答案】 C
【解析】【解答】解:高是:3.14×5=15.7(厘米)
故答案为:C
【分析】圆柱的侧面展开后是一个长方形或正方形,长方形或正方形的一条边与底面周长相等,另一条边与高相等;当底面周长和高相等时侧面展开就是一个正方形.
4.【答案】 C
【解析】【解答】直径:高=d:=1:
故答案为:C
【分析】题意可知,圆柱侧面展开图是正方形时,圆柱的底面周长等于圆柱的高。底面直径和高的比也就是底面直径和底面周长的比。
二、判断题
5.【答案】 错误
【解析】【解答】 将圆柱的侧面沿高展开有可能是长方形,也有可能是正方形,原题说法错误。
故答案为:错误。
【分析】 此题主要考查了圆柱的展开图,把一个圆柱沿高展开,当圆柱的底面周长等于圆柱的高时,展开图是正方形;当圆柱的底面周长不等于圆柱的高时,展开图是长方形;当把一个圆柱不是沿高剪开,而是斜着剪开,得到的图形是平行四边形,据此判断。
6.【答案】 正确
【解析】【解答】20×12=240(平方厘米),原题说法正确.
故答案为:正确.
【分析】根据题意可知,用一张长方形的纸围成一个圆柱,不管怎么围,圆柱的侧面积等于长方形的面积,长方形的面积=长×宽,据此解答.
7.【答案】 错误
【解析】【解答】解:10×1=10(平方米)
故答案为:错误。
【分析】根据题意可知圆柱的侧面积=底面周长×高。
8.【答案】 错误
【解析】【解答】当圆柱体的底面周长等于高时,侧面展开图是正方形,原题说法错误.
故答案为:错误.
【分析】如果圆柱体的侧面展开图是正方形,得到的正方形一条边是圆柱体的高,另一条边是圆柱体的底面周长,因为正方形的四条边相等,所以当圆柱体的侧面展开图是正方形,圆柱体的底面周长等于高,据此判断.
三、填空题
9.【答案】 9.42
【解析】【解答】:14.13
=14.13
=9.42(毫升)
【分析】:因为等底等高的圆锥体积是圆柱的, 所以在装满水圆柱形容器里,放入一个等底等高的圆锥体后,水会溢出和圆锥的体积相等的水,即溢出14.13毫升的, 由此可得容器内还剩下的水,由此即可解答。
10.【答案】 244.92平方分米;282.6立方分米
【解析】【解答】底面半径:
18.84÷3.14÷2
=6÷2
=3(dm)
表面积:
18.84×10+3.14×32×2
=18.84×10+3.14×9×2
=188.4+56.52
=244.92(平方分米)
体积:
3.14×32×10
=3.14×9×10
=28.26×10
=282.6(立方分米)
故答案为:244.92平方分米;282.6立方分米.
【分析】已知圆柱的底面周长和高,要求表面积和体积,先求出圆柱的底面半径,用公式:C÷π÷2=r,要求表面积,用公式:S=Ch+2πr2 , 要求体积,用公式:V=πr2h,据此列式解答.
11.【答案】 213.52;188.4
【解析】【解答】4÷2=2(cm);
圆柱的表面积:
3.14×4×15+3.14×22×2
=3.14×4×15+3.14×4×2
=12.56×15+12.56×2
=188.4+25.12
=213.52(cm2)
圆柱的体积:
3.14×22×15
=3.14×4×15
=12.56×15
=188.4(cm3)
故答案为:213.52;188.4 。
【分析】已知圆柱的底面直径和高,先求出圆柱的底面半径,用直径÷2=半径,要求圆柱的表面积,用公式:圆柱的表面积=圆柱的侧面积+底面积×2,据此列式解答;
要求圆柱的体积,用公式:圆柱的体积=底面积×高,据此列式解答.
四、解答题
12.【答案】 (1)解:40×4+20×4+30
=160+80+30
=240+30
=270(厘米)
答: 捆扎这个蛋糕盒至少要用绸带270厘米。
(2)125.6cm;20cm;2512cm2
【解析】【解答】(2) 如果要在这个盒子的整个侧面贴一张产品说明(如下图),那么圆柱形蛋糕盒的底面周长是125.6cm,圆柱形蛋糕盒的高是20cm,圆柱形蛋糕盒的侧面积是2512cm2。
【分析】(1)观察图可知, 捆扎这个蛋糕盒需要的绸带长度=底面直径×4+高×4+打结用去的绸带长度,据此列式解答;
(2)观察图可知,圆柱的侧面沿高展开,得到一共长方形,长方形的长是圆柱的底面周长,长方形的宽是圆柱的高,长方形的面积是圆柱的侧面积,据此解答。
13.【答案】 解:S=3.14×4×11=138.16(cm2)
V=3.14×(10÷2)2×11-3.14×(4÷2)2×11=725.34(cm3)
答:内芯需要138.16cm2的硬纸壳,这卷纸的实际体积是725.34cm3。
【解析】【分析】内芯需要硬纸壳的面积=卷纸内壁的侧面积=内芯的直径×π×h;
这卷纸的实际体积=这卷纸实心的体积-掏去的内芯的体积,其中这卷纸实心的体积=(整个卷纸的直径÷2)2×π×h,掏去的内芯的体积=(内芯的直径÷2)2×π×h。
五、应用题
14.【答案】解:圆筒的底面周长是30厘米
30×30=900(平方厘米)
答:圆筒的底面周长是30厘米;侧面积是900平方厘米。
【解析】【分析】根据圆柱的侧面展开图的特点,圆筒的底面周长是正方形的边长;正方形的面积正好是这个圆柱体的侧面积.利用正方形的面积公式即可解答。
