2021—2022学年人教版八年级数学下册18.2.2菱形课后练习(Word版含答案)
文档属性
| 名称 | 2021—2022学年人教版八年级数学下册18.2.2菱形课后练习(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 284.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-21 15:22:03 | ||
图片预览

文档简介
2021——2022学年度人教版八年级数学下册 第十八章 平行四边形
18.2.2菱形 课后练习
一、选择题
1.下列命题中正确的是( )
A.对角线互相垂直的四边形是菱形 B.有一个角是直角的四边形是矩形
C.对角线互相平分且相等的四边形是矩形 D.邻边相等的四边形是菱形
2.如图,菱形的对角线相交于点O,点E是边的中点,若,则的长是( )
A.6 B.5 C.4 D.3
3.如图,菱形的对角线、相交于点,,,为过点的一条直线,则图中阴影部分的面积为( )
A.4 B.6 C.8 D.12
4.如图,在的两边上分别截取,,使;再分别以点A,B为圆心,长为半径作弧,两弧交于点C;再连接AC,BC,AB,OC.若,,则四边形的面积是( )
A. B.8 C.4 D.
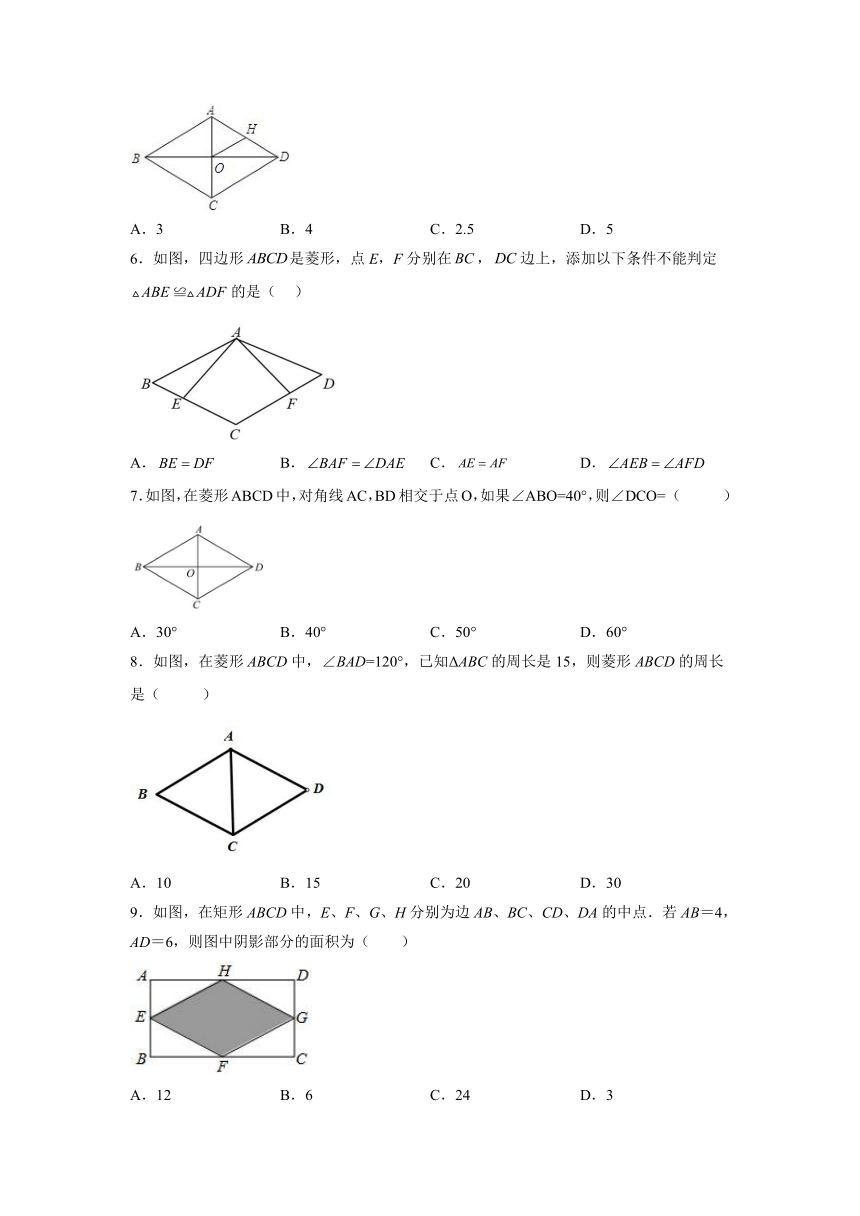
5.如图,菱形ABCD的对角线AC、BD的长分别为6和8,O为AC、BD的交点,H为AB上的中点,则OH的长度为( )
A.3 B.4 C.2.5 D.5
6.如图,四边形是菱形,点E,F分别在,边上,添加以下条件不能判定的是( )
A. B. C. D.
7.如图,在菱形ABCD中,对角线AC,BD相交于点O,如果∠ABO=40°,则∠DCO= ( )
A.30° B.40° C.50° D.60°
8.如图,在菱形ABCD中,∠BAD=120°,已知ΔABC的周长是15,则菱形ABCD的周长是( )
A.10 B.15 C.20 D.30
9.如图,在矩形ABCD中,E、F、G、H分别为边AB、BC、CD、DA的中点.若AB=4,AD=6,则图中阴影部分的面积为( )
A.12 B.6 C.24 D.3
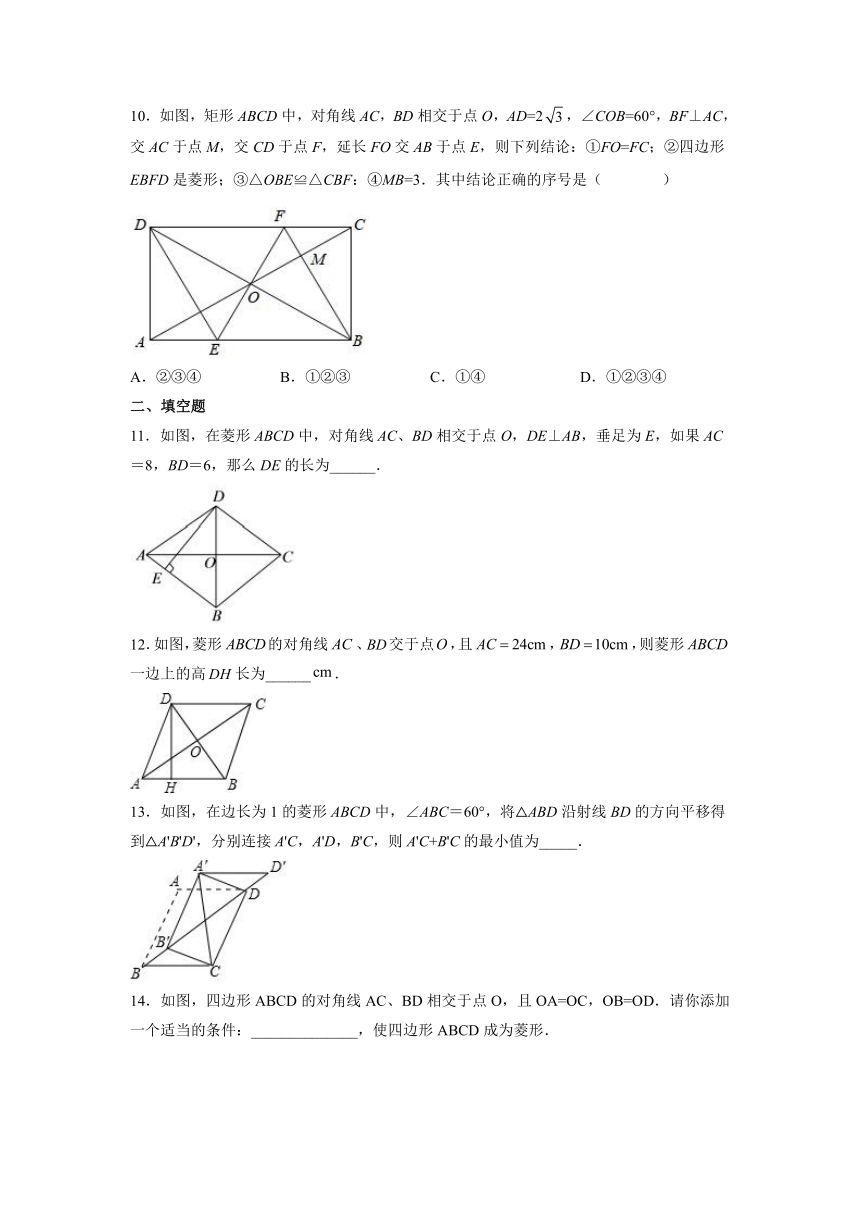
10.如图,矩形ABCD中,对角线AC,BD相交于点O,AD=2,∠COB=60°,BF⊥AC,交AC于点M,交CD于点F,延长FO交AB于点E,则下列结论:①FO=FC;②四边形EBFD是菱形;③△OBE≌△CBF:④MB=3.其中结论正确的序号是( )
A.②③④ B.①②③ C.①④ D.①②③④
二、填空题
11.如图,在菱形ABCD中,对角线AC、BD相交于点O,DE⊥AB,垂足为E,如果AC=8,BD=6,那么DE的长为______.
12.如图,菱形的对角线、交于点,且,,则菱形一边上的高长为______.
13.如图,在边长为1的菱形ABCD中,∠ABC=60°,将△ABD沿射线BD的方向平移得到△A'B'D',分别连接A'C,A'D,B'C,则A'C+B'C的最小值为_____.
14.如图,四边形ABCD的对角线AC、BD相交于点O,且OA=OC,OB=OD.请你添加一个适当的条件:______________,使四边形ABCD成为菱形.
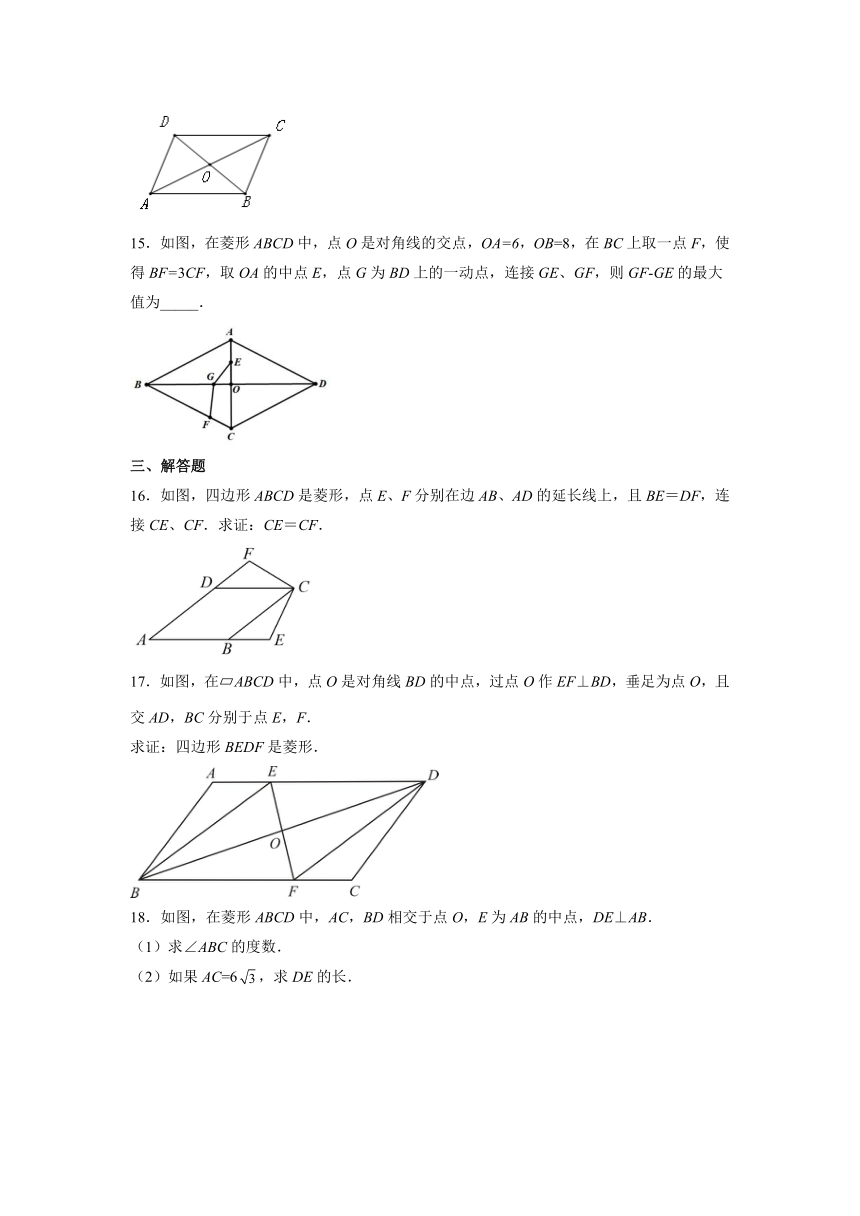
15.如图,在菱形ABCD中,点O是对角线的交点,OA=6,OB=8,在BC上取一点F,使得BF=3CF,取OA的中点E,点G为BD上的一动点,连接GE、GF,则GF-GE的最大值为_____.
三、解答题
16.如图,四边形ABCD是菱形,点E、F分别在边AB、AD的延长线上,且BE=DF,连接CE、CF.求证:CE=CF.
17.如图,在 ABCD中,点O是对角线BD的中点,过点O作EF⊥BD,垂足为点O,且交AD,BC分别于点E,F.
求证:四边形BEDF是菱形.
18.如图,在菱形ABCD中,AC,BD相交于点O,E为AB的中点,DE⊥AB.
(1)求∠ABC的度数.
(2)如果AC=6,求DE的长.
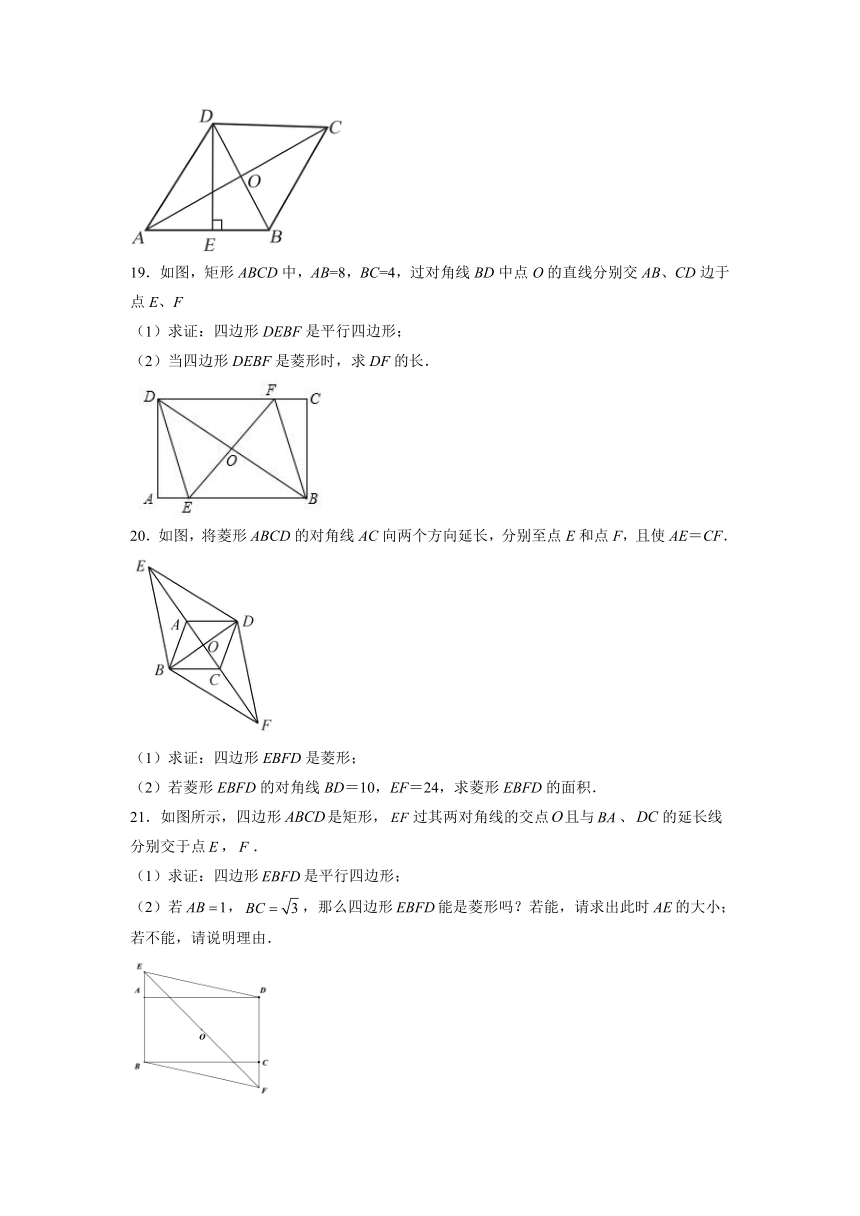
19.如图,矩形ABCD中,AB=8,BC=4,过对角线BD中点O的直线分别交AB、CD边于点E、F
(1)求证:四边形DEBF是平行四边形;
(2)当四边形DEBF是菱形时,求DF的长.
20.如图,将菱形ABCD的对角线AC向两个方向延长,分别至点E和点F,且使AE=CF.
(1)求证:四边形EBFD是菱形;
(2)若菱形EBFD的对角线BD=10,EF=24,求菱形EBFD的面积.
21.如图所示,四边形是矩形,过其两对角线的交点且与、的延长线分别交于点,.
(1)求证:四边形是平行四边形;
(2)若,,那么四边形能是菱形吗?若能,请求出此时的大小;若不能,请说明理由.
22.如图,在Rt△ABC中,∠ACB=90°,D为AB的中点,AE∥CD,CE∥AB,连接DE交AC于点O.
(1)证明:四边形ADCE为菱形.
(2)若∠B=60°,BC=8,求菱形ADCE的高.
23.如图,在菱形ABCD中,对角线AC,BD交于点O,过点A作AE⊥BC于点E,延长BC到点F,使得CF=BE,连接DF,
(1)求证:四边形AEFD是矩形;
(2)连接OE,若AB=5,OE=,求AE的长
【参考答案】
1.C 2.A 3.B 4.C 5.C 6.C 7.C 8.C 9.A 10.D
11.4.8
12.
13.
14.AB=AD.
15.
16.∵四边形ABCD是菱形,
∴CD=CB,∠ABC=∠ADC,
∵∠ABC+∠CBE=180°,∠ADC+∠CDF=180°,
∴∠CBE=∠CDF,
在△CDF和△CBE中,
∴△CDF≌△CBE(SAS),
∴CE=CF.
17.证明:∵四边形ABCD是平行四边形,O为对角线BD的中点,
∴BO=DO,AD∥BC,
∴∠EDB=∠FBO,
在△EOD和△FOB中,,
∴△DOE≌△BOF(ASA);
∴OE=OF,
又∵OB=OD,
∴四边形BEDF是平行四边形,
∵EF⊥BD,
∴平行四边形BEDF为菱形.
18.解:(1)∵E为AB中点,DE⊥AB ,
∴AE=BE,∠AED=∠BED,
又DE=DE,
∴△AED≌△BED,
∴AD=BD,
又∵四边形ABCD是菱形,
∴AD=AB,∠DAB+∠ABC=180°,
∴△ABD是等边三角形 ,
∴∠DAB=60°,
∴∠ABC=120°,
(2)∵四边形ABCD为菱形,AC=6,
∴AC⊥BD,AO=AC=3,
在等边△ABD中,∵AO⊥BD,DE⊥AB,
∴S△ABD= AO×BD=DE×AB,
∴DE=AO =3.
19.(1)证明:∵四边形ABCD是矩形,O是BD的中点,
∴∠A=90°,AD=BC=4,AB∥DC,OB=OD,
∴∠OBE=∠ODF,
又∵∠BOE=∠DOF,
∴△BOE≌△DOF(ASA),
∴EO=FO,
又∵OB=OD,
∴四边形BEDF是平行四边形;
(2)当四边形BEDF是菱形时,BE=DE=DF,
设BE=x,则 DE=x,AE=AB-BE=8﹣x,
在Rt△ADE中,DE2=AD2+AE2,
∴x2=42+(8﹣x)2,
解得:x= ,
∴DF=BE=5.
20.(1)证明:∵菱形ABCD的对角线AC,BD相交于点O,
∴OA=OC,OB=OD,AC⊥BD.
∵AE=CF,
∴OA+AE=OC+CF,即OE=OF.
∴四边形AECF是平行四边形.
∵AC⊥EF,
∴四边形EBFD是菱形.
(2)解:菱形EBFD的面积=.
21.(1)连接,如图,
四边形是矩形,
,
,
点是矩形对角线的交点,
,
,
,
,
四边形是平行四边形;
(2)四边形能是菱形,
连接,如图,
四边形是矩形,
,
,,
,
,
,
,
,
若四边形是菱形,
则,
,
,
,
当时,四边形是菱形.
22.(1)证明:∵AE//CD,CE//AB,
∴四边形ADCE是平行四边形,
∵∠ACB=90°,D为AB的中点,
∴CD=AB=AD,
∴四边形ADCE为菱形;
(2)解:过点D作DF⊥CE,垂足为点F,如图所示:
DF即为菱形ADCE的高,
∵∠B=60°,CD=BD,
∴△BCD是等边三角形,
∴∠BDC=∠BCD=60°,CD=BC=8,
∵CE//AB,
∴∠DCE=∠BDC=60°,
∴∠CDF=30°,
又∵CD=BC=8,
∴CF=4,
∴在Rt△CDF中,DF==4
菱形ADCE的高为.
23.(1)证明:∵四边形ABCD是菱形,
∴ AD∥BC且AD=BC,
∵ BE=CF,
∴ BC=EF,
∴ AD=EF,
∵ AD∥EF,
∴ 四边形AEFD是平行四边形,
∵ AE⊥BC, 即 ∠AEF=90°,
∴ 四边形AEFD是矩形
(2)解:∵ 四边形ABCD是菱形,AB=5,
∴ BC=AB=5,AC⊥BD,OA=OC=AC,OB=OD=BD,
∵ AE⊥BC,即∠AEC=90°,
∴ OE=AC=OA=,AC=2OE=2,
∴ ,
∴ BD=2OB=4,
∵ 菱形ABCD的面积=BD×AC=BC×AE,
即×4×2=5×AE,
解得:AE=4
18.2.2菱形 课后练习
一、选择题
1.下列命题中正确的是( )
A.对角线互相垂直的四边形是菱形 B.有一个角是直角的四边形是矩形
C.对角线互相平分且相等的四边形是矩形 D.邻边相等的四边形是菱形
2.如图,菱形的对角线相交于点O,点E是边的中点,若,则的长是( )
A.6 B.5 C.4 D.3
3.如图,菱形的对角线、相交于点,,,为过点的一条直线,则图中阴影部分的面积为( )
A.4 B.6 C.8 D.12
4.如图,在的两边上分别截取,,使;再分别以点A,B为圆心,长为半径作弧,两弧交于点C;再连接AC,BC,AB,OC.若,,则四边形的面积是( )
A. B.8 C.4 D.
5.如图,菱形ABCD的对角线AC、BD的长分别为6和8,O为AC、BD的交点,H为AB上的中点,则OH的长度为( )
A.3 B.4 C.2.5 D.5
6.如图,四边形是菱形,点E,F分别在,边上,添加以下条件不能判定的是( )
A. B. C. D.
7.如图,在菱形ABCD中,对角线AC,BD相交于点O,如果∠ABO=40°,则∠DCO= ( )
A.30° B.40° C.50° D.60°
8.如图,在菱形ABCD中,∠BAD=120°,已知ΔABC的周长是15,则菱形ABCD的周长是( )
A.10 B.15 C.20 D.30
9.如图,在矩形ABCD中,E、F、G、H分别为边AB、BC、CD、DA的中点.若AB=4,AD=6,则图中阴影部分的面积为( )
A.12 B.6 C.24 D.3
10.如图,矩形ABCD中,对角线AC,BD相交于点O,AD=2,∠COB=60°,BF⊥AC,交AC于点M,交CD于点F,延长FO交AB于点E,则下列结论:①FO=FC;②四边形EBFD是菱形;③△OBE≌△CBF:④MB=3.其中结论正确的序号是( )
A.②③④ B.①②③ C.①④ D.①②③④
二、填空题
11.如图,在菱形ABCD中,对角线AC、BD相交于点O,DE⊥AB,垂足为E,如果AC=8,BD=6,那么DE的长为______.
12.如图,菱形的对角线、交于点,且,,则菱形一边上的高长为______.
13.如图,在边长为1的菱形ABCD中,∠ABC=60°,将△ABD沿射线BD的方向平移得到△A'B'D',分别连接A'C,A'D,B'C,则A'C+B'C的最小值为_____.
14.如图,四边形ABCD的对角线AC、BD相交于点O,且OA=OC,OB=OD.请你添加一个适当的条件:______________,使四边形ABCD成为菱形.
15.如图,在菱形ABCD中,点O是对角线的交点,OA=6,OB=8,在BC上取一点F,使得BF=3CF,取OA的中点E,点G为BD上的一动点,连接GE、GF,则GF-GE的最大值为_____.
三、解答题
16.如图,四边形ABCD是菱形,点E、F分别在边AB、AD的延长线上,且BE=DF,连接CE、CF.求证:CE=CF.
17.如图,在 ABCD中,点O是对角线BD的中点,过点O作EF⊥BD,垂足为点O,且交AD,BC分别于点E,F.
求证:四边形BEDF是菱形.
18.如图,在菱形ABCD中,AC,BD相交于点O,E为AB的中点,DE⊥AB.
(1)求∠ABC的度数.
(2)如果AC=6,求DE的长.
19.如图,矩形ABCD中,AB=8,BC=4,过对角线BD中点O的直线分别交AB、CD边于点E、F
(1)求证:四边形DEBF是平行四边形;
(2)当四边形DEBF是菱形时,求DF的长.
20.如图,将菱形ABCD的对角线AC向两个方向延长,分别至点E和点F,且使AE=CF.
(1)求证:四边形EBFD是菱形;
(2)若菱形EBFD的对角线BD=10,EF=24,求菱形EBFD的面积.
21.如图所示,四边形是矩形,过其两对角线的交点且与、的延长线分别交于点,.
(1)求证:四边形是平行四边形;
(2)若,,那么四边形能是菱形吗?若能,请求出此时的大小;若不能,请说明理由.
22.如图,在Rt△ABC中,∠ACB=90°,D为AB的中点,AE∥CD,CE∥AB,连接DE交AC于点O.
(1)证明:四边形ADCE为菱形.
(2)若∠B=60°,BC=8,求菱形ADCE的高.
23.如图,在菱形ABCD中,对角线AC,BD交于点O,过点A作AE⊥BC于点E,延长BC到点F,使得CF=BE,连接DF,
(1)求证:四边形AEFD是矩形;
(2)连接OE,若AB=5,OE=,求AE的长
【参考答案】
1.C 2.A 3.B 4.C 5.C 6.C 7.C 8.C 9.A 10.D
11.4.8
12.
13.
14.AB=AD.
15.
16.∵四边形ABCD是菱形,
∴CD=CB,∠ABC=∠ADC,
∵∠ABC+∠CBE=180°,∠ADC+∠CDF=180°,
∴∠CBE=∠CDF,
在△CDF和△CBE中,
∴△CDF≌△CBE(SAS),
∴CE=CF.
17.证明:∵四边形ABCD是平行四边形,O为对角线BD的中点,
∴BO=DO,AD∥BC,
∴∠EDB=∠FBO,
在△EOD和△FOB中,,
∴△DOE≌△BOF(ASA);
∴OE=OF,
又∵OB=OD,
∴四边形BEDF是平行四边形,
∵EF⊥BD,
∴平行四边形BEDF为菱形.
18.解:(1)∵E为AB中点,DE⊥AB ,
∴AE=BE,∠AED=∠BED,
又DE=DE,
∴△AED≌△BED,
∴AD=BD,
又∵四边形ABCD是菱形,
∴AD=AB,∠DAB+∠ABC=180°,
∴△ABD是等边三角形 ,
∴∠DAB=60°,
∴∠ABC=120°,
(2)∵四边形ABCD为菱形,AC=6,
∴AC⊥BD,AO=AC=3,
在等边△ABD中,∵AO⊥BD,DE⊥AB,
∴S△ABD= AO×BD=DE×AB,
∴DE=AO =3.
19.(1)证明:∵四边形ABCD是矩形,O是BD的中点,
∴∠A=90°,AD=BC=4,AB∥DC,OB=OD,
∴∠OBE=∠ODF,
又∵∠BOE=∠DOF,
∴△BOE≌△DOF(ASA),
∴EO=FO,
又∵OB=OD,
∴四边形BEDF是平行四边形;
(2)当四边形BEDF是菱形时,BE=DE=DF,
设BE=x,则 DE=x,AE=AB-BE=8﹣x,
在Rt△ADE中,DE2=AD2+AE2,
∴x2=42+(8﹣x)2,
解得:x= ,
∴DF=BE=5.
20.(1)证明:∵菱形ABCD的对角线AC,BD相交于点O,
∴OA=OC,OB=OD,AC⊥BD.
∵AE=CF,
∴OA+AE=OC+CF,即OE=OF.
∴四边形AECF是平行四边形.
∵AC⊥EF,
∴四边形EBFD是菱形.
(2)解:菱形EBFD的面积=.
21.(1)连接,如图,
四边形是矩形,
,
,
点是矩形对角线的交点,
,
,
,
,
四边形是平行四边形;
(2)四边形能是菱形,
连接,如图,
四边形是矩形,
,
,,
,
,
,
,
,
若四边形是菱形,
则,
,
,
,
当时,四边形是菱形.
22.(1)证明:∵AE//CD,CE//AB,
∴四边形ADCE是平行四边形,
∵∠ACB=90°,D为AB的中点,
∴CD=AB=AD,
∴四边形ADCE为菱形;
(2)解:过点D作DF⊥CE,垂足为点F,如图所示:
DF即为菱形ADCE的高,
∵∠B=60°,CD=BD,
∴△BCD是等边三角形,
∴∠BDC=∠BCD=60°,CD=BC=8,
∵CE//AB,
∴∠DCE=∠BDC=60°,
∴∠CDF=30°,
又∵CD=BC=8,
∴CF=4,
∴在Rt△CDF中,DF==4
菱形ADCE的高为.
23.(1)证明:∵四边形ABCD是菱形,
∴ AD∥BC且AD=BC,
∵ BE=CF,
∴ BC=EF,
∴ AD=EF,
∵ AD∥EF,
∴ 四边形AEFD是平行四边形,
∵ AE⊥BC, 即 ∠AEF=90°,
∴ 四边形AEFD是矩形
(2)解:∵ 四边形ABCD是菱形,AB=5,
∴ BC=AB=5,AC⊥BD,OA=OC=AC,OB=OD=BD,
∵ AE⊥BC,即∠AEC=90°,
∴ OE=AC=OA=,AC=2OE=2,
∴ ,
∴ BD=2OB=4,
∵ 菱形ABCD的面积=BD×AC=BC×AE,
即×4×2=5×AE,
解得:AE=4
