2021-2022学年人教版九年级数学下册27.2.3相似三角形应用举例课时练习(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版九年级数学下册27.2.3相似三角形应用举例课时练习(Word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-21 15:21:59 | ||
图片预览



文档简介
相似三角形应用举例
一、单选题
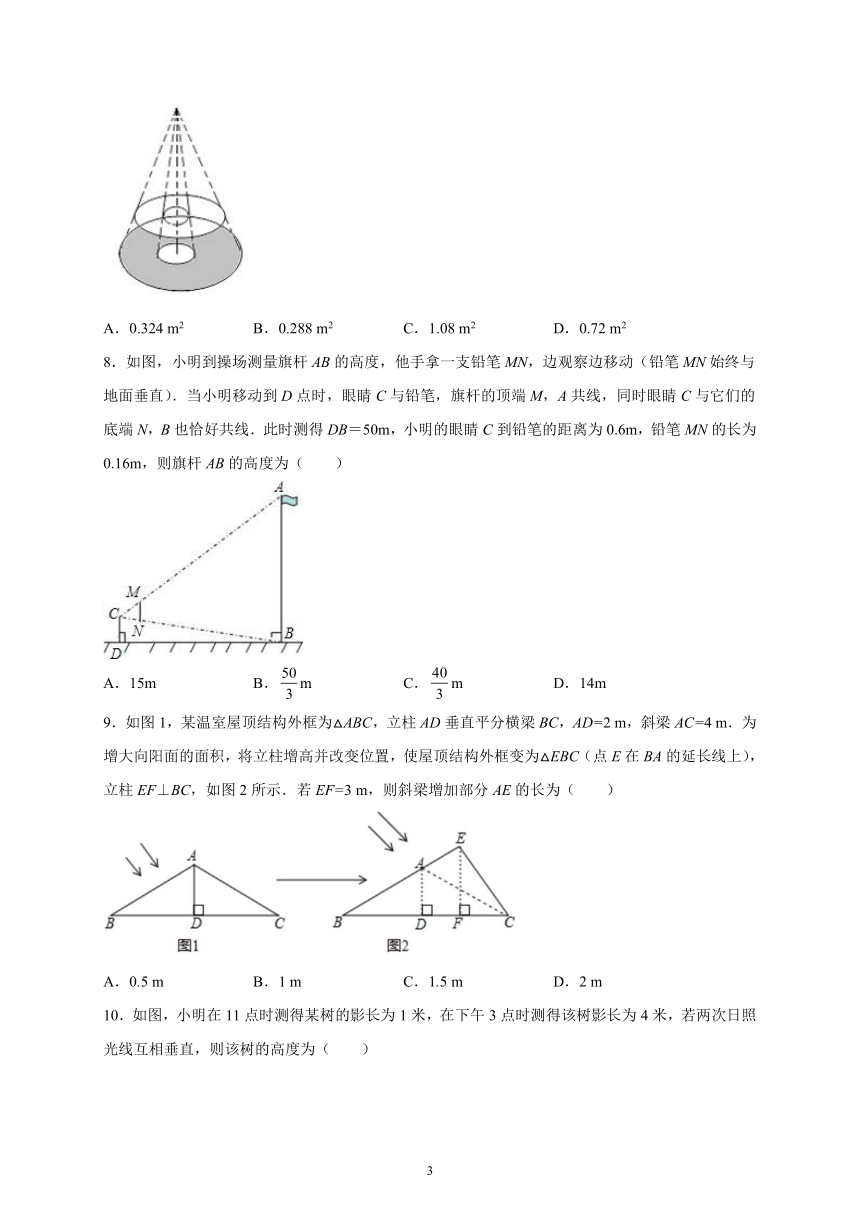
1.据传说,古希腊数学家、天文学家泰勒斯曾利用相似三角形的原理,在金字塔影子的顶部立一根木杆,借助太阳光线构成两个相似三角形,来测量金字塔的高度.已知木杆长,它的影长为,测得为,则金字塔的高度是( )
A. B. C. D.
2.如图,测量小玻璃管口径的量具ABC,AB的长为10cm,AC被分为60等份.如果小玻璃管口DE正好对着量具上20等份处(DE//AB),那么小玻璃管口径DE的长是( )
A. B. C.7cm D.6cm
3.如图,小颖身高为160cm,在阳光下影长AB=210cm,当她走到距离墙角(点D)105cm处时,她的部分影子投射到墙上,则投射在墙上的影子DE的长度为( )cm.
A.30 B.40 C.50 D.80
4.如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上.已知纸板的两条直角边DE=30cm,EF=15cm,测得边DF离地面的高度AC=1.6m,CD=10m,则树高AB长为( )
A.21.6m B.6.6m C.20.6m D.7.6m
5.如图是小孔成像原理的示意图,根据图中标注的尺寸,如果物体AB的高度为36cm,那么它在暗盒中所成的像CD的高度应为( )
A.14cm B.16cm C.25cm D.32cm
6.如图是某数学兴趣小组设计用手电筒来测量某古城墙高度的示意图,在点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处,CD⊥BD,且测得AB=4m,BP=6m,PD=12m,那么该古城墙CD的高度是( )
A.8m B.9m C.16m D.18m
7.圆桌面(桌面中间有一个直径为0.4m的圆洞)正上方的灯泡(看作一个点)发出的光线照射平行于地面的桌面后, 在地面上形成如图所示的圆环形阴影.已知桌面直径为1.2m,桌面离地面1m,若灯泡离地面3m,则地面圆环形阴影的面积是( )
A.0.324 m2 B.0.288 m2 C.1.08 m2 D.0.72 m2
8.如图,小明到操场测量旗杆AB的高度,他手拿一支铅笔MN,边观察边移动(铅笔MN始终与地面垂直).当小明移动到D点时,眼睛C与铅笔,旗杆的顶端M,A共线,同时眼睛C与它们的底端N,B也恰好共线.此时测得DB=50m,小明的眼睛C到铅笔的距离为0.6m,铅笔MN的长为0.16m,则旗杆AB的高度为( )
A.15m B.m C.m D.14m
9.如图1,某温室屋顶结构外框为△ABC,立柱AD垂直平分横梁BC,AD=2 m,斜梁AC=4 m.为增大向阳面的面积,将立柱增高并改变位置,使屋顶结构外框变为△EBC(点E在BA的延长线上),立柱EF⊥BC,如图2所示.若EF=3 m,则斜梁增加部分AE的长为( )
A.0.5 m B.1 m C.1.5 m D.2 m
10.如图,小明在11点时测得某树的影长为1米,在下午3点时测得该树影长为4米,若两次日照光线互相垂直,则该树的高度为( )
A.1米 B.2米 C.3米 D.4米
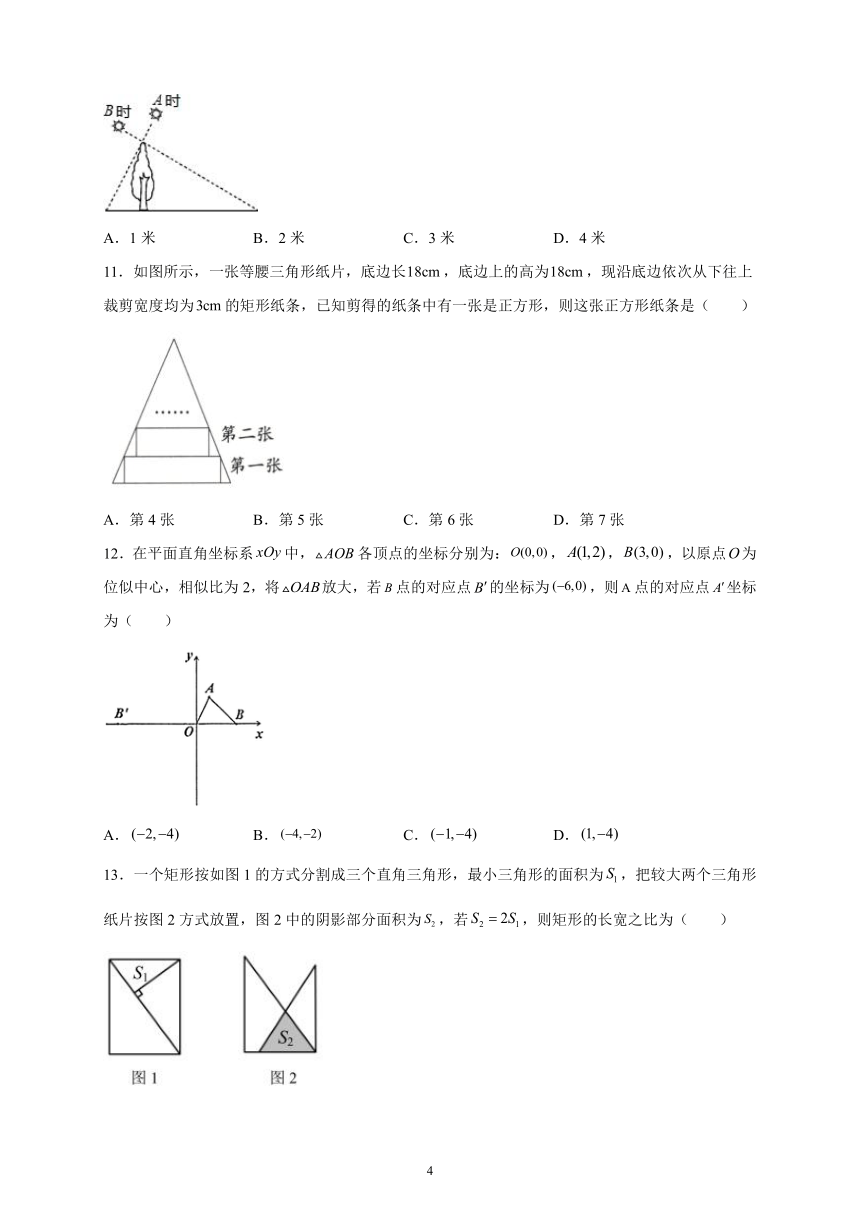
11.如图所示,一张等腰三角形纸片,底边长,底边上的高为,现沿底边依次从下往上裁剪宽度均为的矩形纸条,已知剪得的纸条中有一张是正方形,则这张正方形纸条是( )
A.第4张 B.第5张 C.第6张 D.第7张
12.在平面直角坐标系中,各顶点的坐标分别为:,,,以原点为位似中心,相似比为2,将放大,若点的对应点的坐标为,则点的对应点坐标为( )
A. B. C. D.
13.一个矩形按如图1的方式分割成三个直角三角形,最小三角形的面积为,把较大两个三角形纸片按图2方式放置,图2中的阴影部分面积为,若,则矩形的长宽之比为( )
A.2 B. C. D.
14.《九章算术》是我国数学经典,上面记载:“今有邑方不知大小,各中开门.出北门三十步有木,出西门七百五十步见木.问邑方几何?”其意思是:如图,已知正方形小城ABCD,点E,G分别为CD,AD的中点,EF⊥CD,GH⊥AD,点F,D,H在一条直线上,EF=30步,GH=750步.正方形小城ABCD的边长是( )
A.150步 B.200步 C.250步 D.300步
15.一种雨伞的截面图(如图所示),伞骨,支掌杆,当点沿滑动时,雨伞开闭.若,,此时、两点间的距离等于( )
A. B. C. D.
二、填空题
16.如图,小明在打网球时,要使球恰好能打过网,且落点恰好在离网4米的位置上,已知网高为0.8米,击球点到网的水平距离为3米则球拍击球的高度h为_________米.
17.学校门口的栏杆如图所示,栏杆从水平位置绕点旋转到位置,已知,足分别为,,,,,则栏杆端应下降的垂直距离为________.
18.如图,为了测量一栋楼的高度,王青同学在她脚下放了一面镜子,然后向后退,直到她刚好在镜子里看到楼的顶部,如果王青身高1.55m,她估计自己眼睛距地面1.50m.同时量得LM=30cm,MS=2m,则这栋楼高 _____m.
19.如图所示,一条河流的两岸互相平行,沿南岸有一排大树,每隔4米一棵,沿北岸有一排电线杆,每两根电线杆之间的距离为80米,一同学站在距南岸9米的点P处,正好北岸相邻的两根电线杆被南岸的5棵树遮挡住,那么这条河流的宽度是 _____米.
20.中国是礼仪之邦.从西四环下高速时,小明看到高新区的门户——“礼仪之门”这个雕塑,他想利用所学的数学知识测量它的高度.他在点C处放一镜子,并作一标记,来回走动,走到点D时,看到“礼仪之门”顶点A在镜面中的像与镜面上的标记重合,这时,测得小明眼睛与地面的高度米,米.然后,小明从点D沿DH方向走了19米,到达“礼仪之门”影子的末端G处,此时,测得小明身高米,影长米,则“礼仪之门”的高AB为______米.
三、解答题
21.如图,相邻的两根电线杆都用钢索在地面上固定,一根电线杆钢索系在离地面4米处(),另一根电线杆钢索系在离地面6米处,求中间两根钢索相交处点E离地面的高度EF是多高?
22.某天小明和小亮去某影视基地游玩,当小明给站在城楼上的小亮照相时发现他自己的眼睛、凉亭顶端、小亮头顶三点恰好在一条直线上(如图).已知小明的跟晴离地面米,凉亭顶端离地面米,小明到凉亭的距离为米,凉亭离城楼底部的距离为米,小亮身高为米.请根据以上数据求出城楼的高度.
23.如图,在路灯M下,小明的身高如图中线段AB所示;他在地面上的影子如图中线段AC所示,路灯灯泡在点D正上方.
(1)如果小明的身高AB=1.6m,他的影子长AC=1.4m,且他到路灯的距离AD=2.1m,求灯泡的高.
(2)在(1)的条件下当小明越过路灯到达FG时,发现影长和身高相等,求小明前行的路程.
24.如图①是公园跷跷板的示意图,立柱OC与地面垂直,点C为横板AB的中点.小明和小聪去玩跷跷板,小明最高能将小聪翘到1米高(如图②).
(1)求立柱OC的高度;
(2)小明想要把小聪最高翘到1.25米高,请你帮他找出一种方法,并解答.
25.一块材料的形状是等腰△ABC,底边 BC=120 cm,高 AD=120 cm.
(1)若把这块材料加工成正方形零件,使正方形的一边在 BC 上,其余两个顶点分别在AB,AC 上(如图 1),则这个正方形的边长为多少?
(2)若把这块材料加工成正方体零件(如图 2,阴影部分为正方体展开图),则正方体的表面积为多少?
26.我们知道当人们的视线与物体的表面互相垂直且视线恰好落在物体中心位置时的视觉效果最佳,如图是小然站在地面欣赏悬挂在墙壁上的油画的示意图,设油画与墙壁的夹角,此时小然的眼睛与油画底部处于同一水平线上,视线恰好落在油画的中心位置处,且与垂直.已知油画的长度为.
(1)当小然到墙壁的距离时,求油画顶部点到墙壁的距离;
(2)在(1)的基础上当油画底部处位置不变,油画与墙壁的夹角逐渐减小时则变短,当变为原来的,小然为了保证欣赏油画的视觉效果最佳,他的位置是否发生变化,若不变说明理由;若变化,请你求出变化的方向和距离.
试卷第1页,共3页
参考答案:
1.A
解:设金字塔的高度为,
由题意得:
,
解得:,
故选A .
2.A
解:∵DE//AB,
∴△CDE∽△CAB.
∴DE:AB=CD:AC.
∴40:60=DE:10.
∴DE=.
∴小玻璃管口径DE是.
故选:A.
3.D
解:过E作EF⊥CG于F,
设投射在墙上的影子DE长度为x cm,由题意得:△GFE∽△HAB,
∴,
即
解得:x=80.
经检验,x=80是原方程的解.
故选:D.
4.B
解:依题意,
cm,cm,m,m,
m
m
故选B
5.B
解:如图,过作于 过作于
由小孔成像原理可得:
而
所以(cm),经检验符合题意.
故选B
6.A
解:如图,根据反射的性质可得∠APE=∠CPE
∵EP⊥BD
∴∠APB=∠CPD
∵AB⊥BD,CD⊥BD
∴∠ABP=∠CDP=90°
∴△ABP∽△CDP
∴
∴
故选:A
7.D
解:略
8.C
解:过作于,交于,
根据题意 ,
∵,
∴,
∴四边形是矩形,
,
又,
∴∠CMN=∠A,∠CNM=∠CBA,
,
,
,
.
故选择C.
9.D
解:∵EF⊥BC,AD⊥BC,
∴AD∥EF,
∴△ABD∽△EBF,
∴,
∵AD垂直平分横梁BC,
∴,
∴,解得EB=6(m),
∴AE=EB-AB=6-4=2(m).
10.B
解:根据题意,作△EFC;树高为CD,且∠ECF=90°,FD=4,ED=1;
则∠ECF=∠EDC=∠CDF=90°,
∴∠ECD+∠E=90°,∠ECD+∠FCD=90°,
∴∠E=∠FCD
∴Rt△EDC∽Rt△CDF
∴
即DC2=ED FD,代入数据可得DC2=4,
∴DC=2.
故选:B
11.B
解:已知剪得的纸条中有一张是正方形,则该正方形的边长为,
设从顶点到这个正方形顶边的距离为,
根据相似三角形的性质可得,解得(张),
所以这张正方形纸条是第5张,
故选B.
12.A
解:如图,由题可知OA′:OA=2:1,
∵B′的坐标为(﹣6,0),
∴A′在第三象限,
∴A′(﹣2,﹣4),
故选:A.
13.A
解:如图(1),设的面积为;
如图(2)由题意,知,则
又
矩形的长宽之比为2.
故选A.
14.D
解:∵点E,G分别为CD,AD的中点,
∴,,
∴,
又题意可得,,
∴,
∴,
而EF=30步,GH=750步,
即,
∴,
解得:,
∴步;
15.C
解:,,
,
又,
,
,
∵OE=30cm,
BD=30×3=90cm.
故选:C.
16.1.4
解:如图,
∵DB//EC,
∴△ADB∽△AEC,
∴,即0.8×(4+3)=4h,
∴h=1.4 (m).
故答案为1.4.
17.##m
解:,,
,
又,
,
则,
,,,
,
解得:,
栏杆端应下降的垂直距离为.
故答案为:.
18.10
解:如图,
根据题意,,
,(反射角等于入射角),
,
,即,
所以这栋大楼高为.
故答案为10
19.
解:如图,
∵北岸相邻的两根电线杆被南岸的5棵树遮挡住,
∴,,
∵,
∴,
,
∵,P到AB的距离即,
∴,
解得:,
∴河宽为36米,
故答案为:36.
20.####
解:设,根据题意,
又
米,米
,米,米,
解得
故答案为:
21.
解:作EF⊥BD于F,
∵CD∥AB,
∴△CED∽△BEA,
∴ ,
∴
∵AB∥EF,
∴△DEF∽△DAB,
∴ ,
∴ ,
解得EF=.
答:中间两根钢索的相交处E距地面的高度是 m.
22.米.
解:如图,过点作于点,交于点,
则四边形和四边形都是矩形,
,
由题意得:米,米,米,米,米,
米,米,米,米,
,
,
,即,
解得(米),
则城楼的高度为(米),
答:城楼的高度为米.
23.(1)4m (2)4.5m
(1)
解:如图所示,连接MC(此时根据题意可知C、B、M三点共线),
∵AB∥MD,
∴△ABC∽△DMC,
∴,
∵AC=1.4m,AD=2.1m,
∴CD=3.5m,
∴,
∴,
∴灯泡的高为4m;
(2)
解:如图所示,连接MG并延长交直线CD于H,
同理可证△FGH∽△DMH,
∴,
∴,
∴,
∴小明前行的路程为4.5m.
24.(1)米
(2)设计方法为:要使小明想要把小聪最高翘到1.25米高,只需要将小明距离点的距离变为,即
(1)
解:标注点如下图:
根据题意在和,
,
,
,
分别为的中点,
,
,
(米);
(2)
解:设计方法为:要使小明想要把小聪最高翘到1.25米高,只需要将小明距离点的距离变为,即,过程如下:
根据题意作如下图形,
根据题意在和,
,
,
,
,
,
(米);
小明想要把小聪最高翘到1.25米高,只需要将小明距离点的距离变为,即即可.
25.(1)这个正方形的边长为60cm; (2)正方体的表面积为3456cm2
(1)
解:设正方形的边长为xcm,
∵四边形EFGH是正方形,
∴EH∥BC,EF=EH=xcm,又AD⊥BC,
∴∠AEH=∠ABC,∠AHE=∠ACB,AD⊥EH,DK=EF=xcm,
∴△AEH∽△ABC,
∴,
∵BC=120 cm, AD=120 cm,
∴,
解得:x=60,
答:方形的边长为60cm;
(2)
解:设正方体的棱长为acm,
由题意知:MN∥BC,AP⊥MN,MN=a,PD=4a,
∴△AMN∽△ABC,
∴,即,
解得:a=24
∴正方体的表面积为6×242=3456cm2.
26.(1);(2)变化,小然应该远离墙壁
(1)解:如图所示,过点D作,交PM于点C,
∵,,
∴,
∴,
∵,
∴,
∴,
∴,
∴,
∵,点是的中点,
∴,
∴,
∴
∴油画顶部到墙壁的距离是;
(2)由(1)得,
∵,
∴,
∴,
∴
所以小然位置发生变化,应该远离墙壁.
答案第1页,共2页
一、单选题
1.据传说,古希腊数学家、天文学家泰勒斯曾利用相似三角形的原理,在金字塔影子的顶部立一根木杆,借助太阳光线构成两个相似三角形,来测量金字塔的高度.已知木杆长,它的影长为,测得为,则金字塔的高度是( )
A. B. C. D.
2.如图,测量小玻璃管口径的量具ABC,AB的长为10cm,AC被分为60等份.如果小玻璃管口DE正好对着量具上20等份处(DE//AB),那么小玻璃管口径DE的长是( )
A. B. C.7cm D.6cm
3.如图,小颖身高为160cm,在阳光下影长AB=210cm,当她走到距离墙角(点D)105cm处时,她的部分影子投射到墙上,则投射在墙上的影子DE的长度为( )cm.
A.30 B.40 C.50 D.80
4.如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上.已知纸板的两条直角边DE=30cm,EF=15cm,测得边DF离地面的高度AC=1.6m,CD=10m,则树高AB长为( )
A.21.6m B.6.6m C.20.6m D.7.6m
5.如图是小孔成像原理的示意图,根据图中标注的尺寸,如果物体AB的高度为36cm,那么它在暗盒中所成的像CD的高度应为( )
A.14cm B.16cm C.25cm D.32cm
6.如图是某数学兴趣小组设计用手电筒来测量某古城墙高度的示意图,在点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处,CD⊥BD,且测得AB=4m,BP=6m,PD=12m,那么该古城墙CD的高度是( )
A.8m B.9m C.16m D.18m
7.圆桌面(桌面中间有一个直径为0.4m的圆洞)正上方的灯泡(看作一个点)发出的光线照射平行于地面的桌面后, 在地面上形成如图所示的圆环形阴影.已知桌面直径为1.2m,桌面离地面1m,若灯泡离地面3m,则地面圆环形阴影的面积是( )
A.0.324 m2 B.0.288 m2 C.1.08 m2 D.0.72 m2
8.如图,小明到操场测量旗杆AB的高度,他手拿一支铅笔MN,边观察边移动(铅笔MN始终与地面垂直).当小明移动到D点时,眼睛C与铅笔,旗杆的顶端M,A共线,同时眼睛C与它们的底端N,B也恰好共线.此时测得DB=50m,小明的眼睛C到铅笔的距离为0.6m,铅笔MN的长为0.16m,则旗杆AB的高度为( )
A.15m B.m C.m D.14m
9.如图1,某温室屋顶结构外框为△ABC,立柱AD垂直平分横梁BC,AD=2 m,斜梁AC=4 m.为增大向阳面的面积,将立柱增高并改变位置,使屋顶结构外框变为△EBC(点E在BA的延长线上),立柱EF⊥BC,如图2所示.若EF=3 m,则斜梁增加部分AE的长为( )
A.0.5 m B.1 m C.1.5 m D.2 m
10.如图,小明在11点时测得某树的影长为1米,在下午3点时测得该树影长为4米,若两次日照光线互相垂直,则该树的高度为( )
A.1米 B.2米 C.3米 D.4米
11.如图所示,一张等腰三角形纸片,底边长,底边上的高为,现沿底边依次从下往上裁剪宽度均为的矩形纸条,已知剪得的纸条中有一张是正方形,则这张正方形纸条是( )
A.第4张 B.第5张 C.第6张 D.第7张
12.在平面直角坐标系中,各顶点的坐标分别为:,,,以原点为位似中心,相似比为2,将放大,若点的对应点的坐标为,则点的对应点坐标为( )
A. B. C. D.
13.一个矩形按如图1的方式分割成三个直角三角形,最小三角形的面积为,把较大两个三角形纸片按图2方式放置,图2中的阴影部分面积为,若,则矩形的长宽之比为( )
A.2 B. C. D.
14.《九章算术》是我国数学经典,上面记载:“今有邑方不知大小,各中开门.出北门三十步有木,出西门七百五十步见木.问邑方几何?”其意思是:如图,已知正方形小城ABCD,点E,G分别为CD,AD的中点,EF⊥CD,GH⊥AD,点F,D,H在一条直线上,EF=30步,GH=750步.正方形小城ABCD的边长是( )
A.150步 B.200步 C.250步 D.300步
15.一种雨伞的截面图(如图所示),伞骨,支掌杆,当点沿滑动时,雨伞开闭.若,,此时、两点间的距离等于( )
A. B. C. D.
二、填空题
16.如图,小明在打网球时,要使球恰好能打过网,且落点恰好在离网4米的位置上,已知网高为0.8米,击球点到网的水平距离为3米则球拍击球的高度h为_________米.
17.学校门口的栏杆如图所示,栏杆从水平位置绕点旋转到位置,已知,足分别为,,,,,则栏杆端应下降的垂直距离为________.
18.如图,为了测量一栋楼的高度,王青同学在她脚下放了一面镜子,然后向后退,直到她刚好在镜子里看到楼的顶部,如果王青身高1.55m,她估计自己眼睛距地面1.50m.同时量得LM=30cm,MS=2m,则这栋楼高 _____m.
19.如图所示,一条河流的两岸互相平行,沿南岸有一排大树,每隔4米一棵,沿北岸有一排电线杆,每两根电线杆之间的距离为80米,一同学站在距南岸9米的点P处,正好北岸相邻的两根电线杆被南岸的5棵树遮挡住,那么这条河流的宽度是 _____米.
20.中国是礼仪之邦.从西四环下高速时,小明看到高新区的门户——“礼仪之门”这个雕塑,他想利用所学的数学知识测量它的高度.他在点C处放一镜子,并作一标记,来回走动,走到点D时,看到“礼仪之门”顶点A在镜面中的像与镜面上的标记重合,这时,测得小明眼睛与地面的高度米,米.然后,小明从点D沿DH方向走了19米,到达“礼仪之门”影子的末端G处,此时,测得小明身高米,影长米,则“礼仪之门”的高AB为______米.
三、解答题
21.如图,相邻的两根电线杆都用钢索在地面上固定,一根电线杆钢索系在离地面4米处(),另一根电线杆钢索系在离地面6米处,求中间两根钢索相交处点E离地面的高度EF是多高?
22.某天小明和小亮去某影视基地游玩,当小明给站在城楼上的小亮照相时发现他自己的眼睛、凉亭顶端、小亮头顶三点恰好在一条直线上(如图).已知小明的跟晴离地面米,凉亭顶端离地面米,小明到凉亭的距离为米,凉亭离城楼底部的距离为米,小亮身高为米.请根据以上数据求出城楼的高度.
23.如图,在路灯M下,小明的身高如图中线段AB所示;他在地面上的影子如图中线段AC所示,路灯灯泡在点D正上方.
(1)如果小明的身高AB=1.6m,他的影子长AC=1.4m,且他到路灯的距离AD=2.1m,求灯泡的高.
(2)在(1)的条件下当小明越过路灯到达FG时,发现影长和身高相等,求小明前行的路程.
24.如图①是公园跷跷板的示意图,立柱OC与地面垂直,点C为横板AB的中点.小明和小聪去玩跷跷板,小明最高能将小聪翘到1米高(如图②).
(1)求立柱OC的高度;
(2)小明想要把小聪最高翘到1.25米高,请你帮他找出一种方法,并解答.
25.一块材料的形状是等腰△ABC,底边 BC=120 cm,高 AD=120 cm.
(1)若把这块材料加工成正方形零件,使正方形的一边在 BC 上,其余两个顶点分别在AB,AC 上(如图 1),则这个正方形的边长为多少?
(2)若把这块材料加工成正方体零件(如图 2,阴影部分为正方体展开图),则正方体的表面积为多少?
26.我们知道当人们的视线与物体的表面互相垂直且视线恰好落在物体中心位置时的视觉效果最佳,如图是小然站在地面欣赏悬挂在墙壁上的油画的示意图,设油画与墙壁的夹角,此时小然的眼睛与油画底部处于同一水平线上,视线恰好落在油画的中心位置处,且与垂直.已知油画的长度为.
(1)当小然到墙壁的距离时,求油画顶部点到墙壁的距离;
(2)在(1)的基础上当油画底部处位置不变,油画与墙壁的夹角逐渐减小时则变短,当变为原来的,小然为了保证欣赏油画的视觉效果最佳,他的位置是否发生变化,若不变说明理由;若变化,请你求出变化的方向和距离.
试卷第1页,共3页
参考答案:
1.A
解:设金字塔的高度为,
由题意得:
,
解得:,
故选A .
2.A
解:∵DE//AB,
∴△CDE∽△CAB.
∴DE:AB=CD:AC.
∴40:60=DE:10.
∴DE=.
∴小玻璃管口径DE是.
故选:A.
3.D
解:过E作EF⊥CG于F,
设投射在墙上的影子DE长度为x cm,由题意得:△GFE∽△HAB,
∴,
即
解得:x=80.
经检验,x=80是原方程的解.
故选:D.
4.B
解:依题意,
cm,cm,m,m,
m
m
故选B
5.B
解:如图,过作于 过作于
由小孔成像原理可得:
而
所以(cm),经检验符合题意.
故选B
6.A
解:如图,根据反射的性质可得∠APE=∠CPE
∵EP⊥BD
∴∠APB=∠CPD
∵AB⊥BD,CD⊥BD
∴∠ABP=∠CDP=90°
∴△ABP∽△CDP
∴
∴
故选:A
7.D
解:略
8.C
解:过作于,交于,
根据题意 ,
∵,
∴,
∴四边形是矩形,
,
又,
∴∠CMN=∠A,∠CNM=∠CBA,
,
,
,
.
故选择C.
9.D
解:∵EF⊥BC,AD⊥BC,
∴AD∥EF,
∴△ABD∽△EBF,
∴,
∵AD垂直平分横梁BC,
∴,
∴,解得EB=6(m),
∴AE=EB-AB=6-4=2(m).
10.B
解:根据题意,作△EFC;树高为CD,且∠ECF=90°,FD=4,ED=1;
则∠ECF=∠EDC=∠CDF=90°,
∴∠ECD+∠E=90°,∠ECD+∠FCD=90°,
∴∠E=∠FCD
∴Rt△EDC∽Rt△CDF
∴
即DC2=ED FD,代入数据可得DC2=4,
∴DC=2.
故选:B
11.B
解:已知剪得的纸条中有一张是正方形,则该正方形的边长为,
设从顶点到这个正方形顶边的距离为,
根据相似三角形的性质可得,解得(张),
所以这张正方形纸条是第5张,
故选B.
12.A
解:如图,由题可知OA′:OA=2:1,
∵B′的坐标为(﹣6,0),
∴A′在第三象限,
∴A′(﹣2,﹣4),
故选:A.
13.A
解:如图(1),设的面积为;
如图(2)由题意,知,则
又
矩形的长宽之比为2.
故选A.
14.D
解:∵点E,G分别为CD,AD的中点,
∴,,
∴,
又题意可得,,
∴,
∴,
而EF=30步,GH=750步,
即,
∴,
解得:,
∴步;
15.C
解:,,
,
又,
,
,
∵OE=30cm,
BD=30×3=90cm.
故选:C.
16.1.4
解:如图,
∵DB//EC,
∴△ADB∽△AEC,
∴,即0.8×(4+3)=4h,
∴h=1.4 (m).
故答案为1.4.
17.##m
解:,,
,
又,
,
则,
,,,
,
解得:,
栏杆端应下降的垂直距离为.
故答案为:.
18.10
解:如图,
根据题意,,
,(反射角等于入射角),
,
,即,
所以这栋大楼高为.
故答案为10
19.
解:如图,
∵北岸相邻的两根电线杆被南岸的5棵树遮挡住,
∴,,
∵,
∴,
,
∵,P到AB的距离即,
∴,
解得:,
∴河宽为36米,
故答案为:36.
20.####
解:设,根据题意,
又
米,米
,米,米,
解得
故答案为:
21.
解:作EF⊥BD于F,
∵CD∥AB,
∴△CED∽△BEA,
∴ ,
∴
∵AB∥EF,
∴△DEF∽△DAB,
∴ ,
∴ ,
解得EF=.
答:中间两根钢索的相交处E距地面的高度是 m.
22.米.
解:如图,过点作于点,交于点,
则四边形和四边形都是矩形,
,
由题意得:米,米,米,米,米,
米,米,米,米,
,
,
,即,
解得(米),
则城楼的高度为(米),
答:城楼的高度为米.
23.(1)4m (2)4.5m
(1)
解:如图所示,连接MC(此时根据题意可知C、B、M三点共线),
∵AB∥MD,
∴△ABC∽△DMC,
∴,
∵AC=1.4m,AD=2.1m,
∴CD=3.5m,
∴,
∴,
∴灯泡的高为4m;
(2)
解:如图所示,连接MG并延长交直线CD于H,
同理可证△FGH∽△DMH,
∴,
∴,
∴,
∴小明前行的路程为4.5m.
24.(1)米
(2)设计方法为:要使小明想要把小聪最高翘到1.25米高,只需要将小明距离点的距离变为,即
(1)
解:标注点如下图:
根据题意在和,
,
,
,
分别为的中点,
,
,
(米);
(2)
解:设计方法为:要使小明想要把小聪最高翘到1.25米高,只需要将小明距离点的距离变为,即,过程如下:
根据题意作如下图形,
根据题意在和,
,
,
,
,
,
(米);
小明想要把小聪最高翘到1.25米高,只需要将小明距离点的距离变为,即即可.
25.(1)这个正方形的边长为60cm; (2)正方体的表面积为3456cm2
(1)
解:设正方形的边长为xcm,
∵四边形EFGH是正方形,
∴EH∥BC,EF=EH=xcm,又AD⊥BC,
∴∠AEH=∠ABC,∠AHE=∠ACB,AD⊥EH,DK=EF=xcm,
∴△AEH∽△ABC,
∴,
∵BC=120 cm, AD=120 cm,
∴,
解得:x=60,
答:方形的边长为60cm;
(2)
解:设正方体的棱长为acm,
由题意知:MN∥BC,AP⊥MN,MN=a,PD=4a,
∴△AMN∽△ABC,
∴,即,
解得:a=24
∴正方体的表面积为6×242=3456cm2.
26.(1);(2)变化,小然应该远离墙壁
(1)解:如图所示,过点D作,交PM于点C,
∵,,
∴,
∴,
∵,
∴,
∴,
∴,
∴,
∵,点是的中点,
∴,
∴,
∴
∴油画顶部到墙壁的距离是;
(2)由(1)得,
∵,
∴,
∴,
∴
所以小然位置发生变化,应该远离墙壁.
答案第1页,共2页
