指数函数与对数函数的关系
图片预览




文档简介
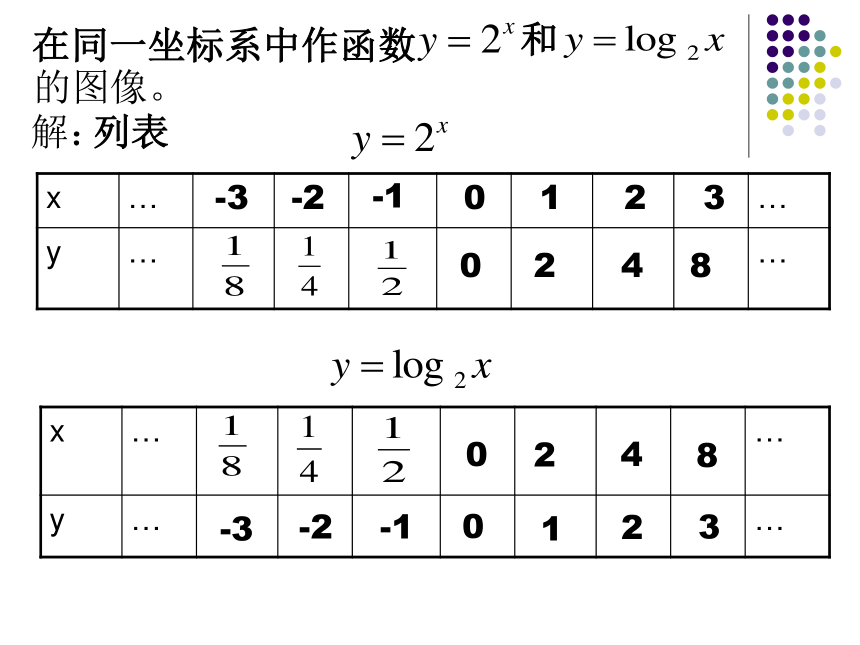
课件20张PPT。函数函数函数函数3.2.3指数函数与对数函数的关系在同一坐标系中作函数的图像。解:列表和-3
-2-100
1
22438-3
-2-10
02
142
83
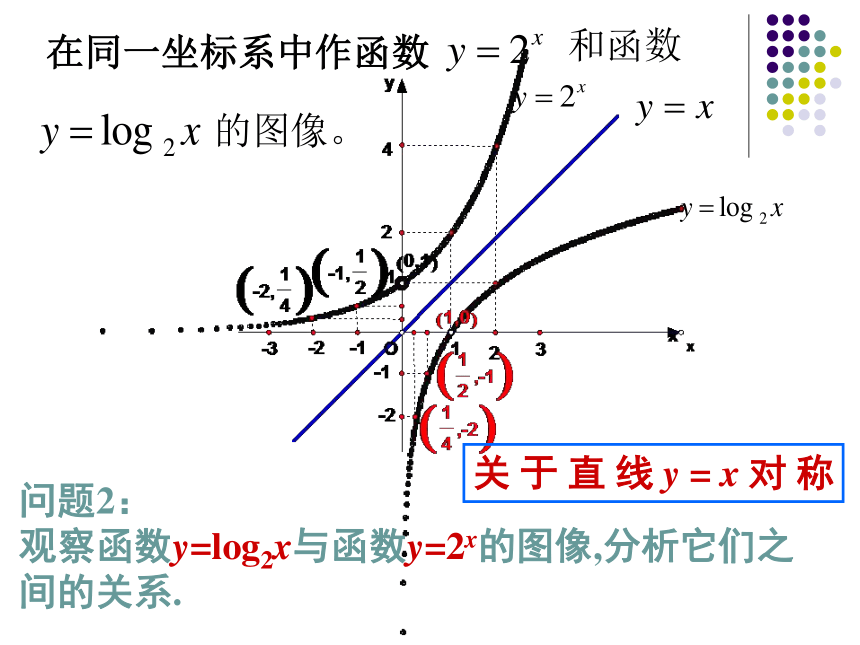
在同一坐标系中作函数和函数的图像。问题2:
观察函数y=log2x与函数y=2x的图像,分析它们之间的关系.关于直线y=x对称同底的指数函数和对数函数的图象
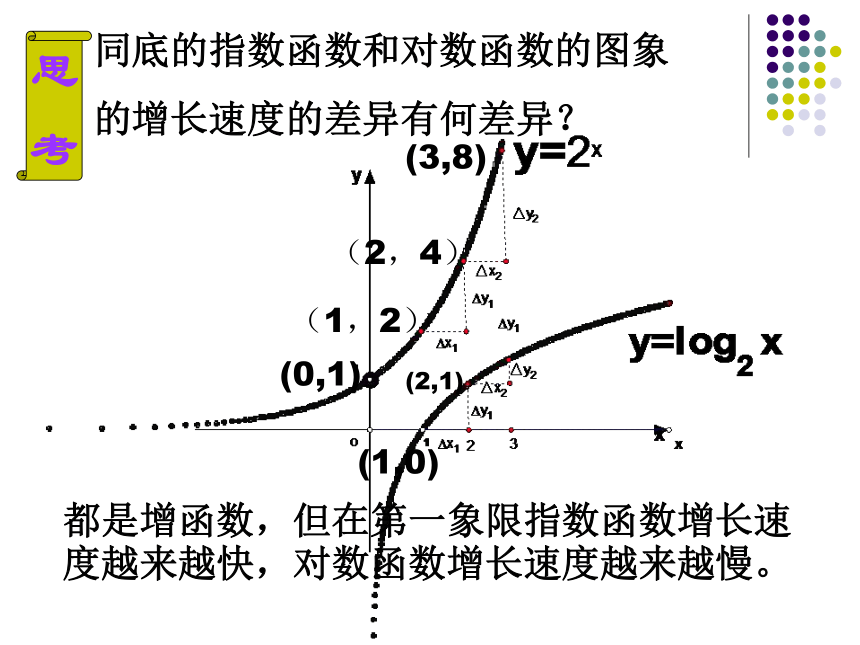
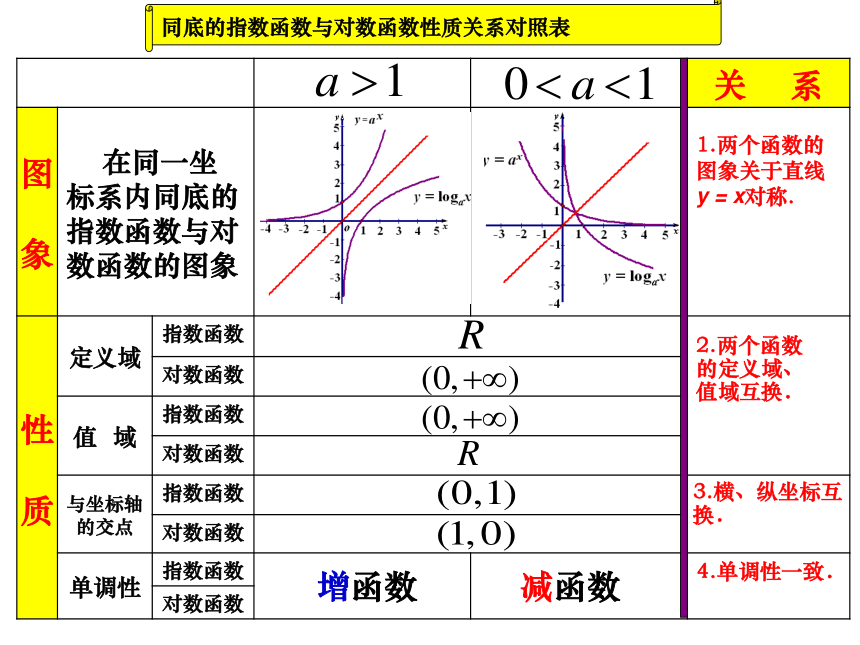
的增长速度的差异有何差异?思 考都是增函数,但在第一象限指数函数增长速度越来越快,对数函数增长速度越来越慢。同底的指数函数与对数函数性质关系对照表 1.两个函数的图象关于直线
y = x对称.2.两个函数的定义域、值域互换.3.横、纵坐标互换.4.单调性一致.增函数减函数问题1:
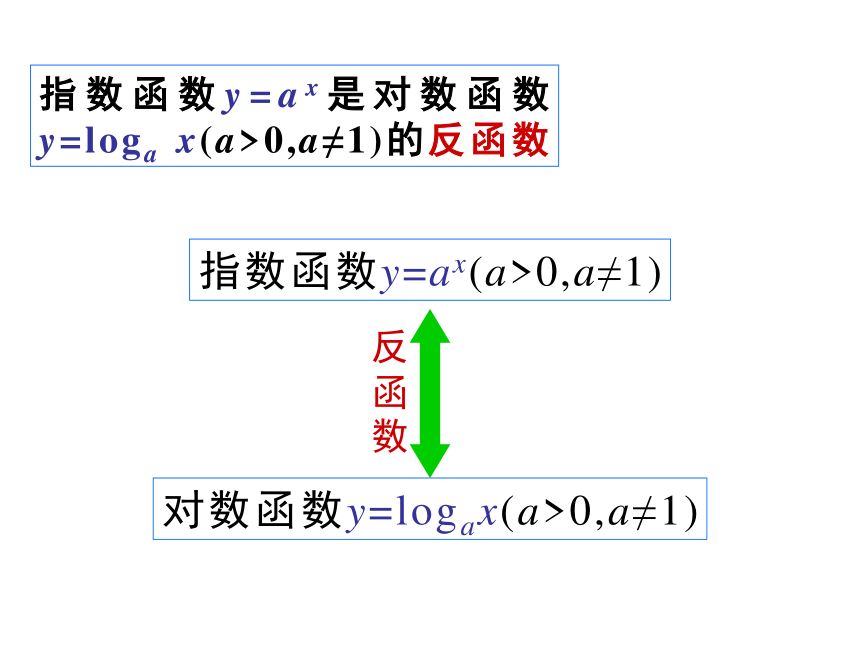
指数函数y=ax与对数函数y=loga x(a>0,a≠1)有什么关系?称这两个函数互为反函数y=axx=loga yy=loga x指数换对数交换x,yy=3x+5交换x,y移项指数函数y=ax(a>0,a≠1)对数函数y=logax(a>0,a≠1)指数函数y=ax是对数函数y=loga x(a>0,a≠1)的反函数1.一一映射的函数才有反函数。
2.对数函数y=loga x与指数函数y=ax互为反函数。
3.互为反函数的图象关于直线y=x对称。
4.函数y=f(x)的反函数通常用y=f-1(x) 表示。
注意:y=f-1(x) 读作:“f逆x”
表示反函数,不是-1次幂(倒数)的意思例1 写出下列对数函数的反函数:
(1)y =lgx; 解(1)y=10x(2)x、y互换得反函数x、y互换得反函数例2 写出下列指数函数的反函数:
(1) y=5x 例3 求函数y=3x-2(x>0)反函数,并在同一直角坐标系中作出函数及其反函数的图象。解:由y=3x-2(x>0 )得 (y>-2 )所以y=3x-2(x∈R)的反函数是(x>-2 )y=3x-2 经过两点(0,-2), (2/3,0)做一做y=3x-2y=x求函数反函数的步骤:3? 求原函数的值域1? 反解2? x与y互换4? 写出反函数及它的定义域 练1:求下列函数的反函数:结论1:互为反函数的两个函数定义域、值域互换。解:练2:下列函数与练习1中的函数结论2:只有一一映射的函数才有反函数。有何异同?此函数是否有反函数?b=f(a)a=f-1(b)点(b,a)在反函数y=f-1(x) 的图像上点(a,b)在函数y=f(x)的图像上结论:[例4]函数f(x)=loga (x-1)(a>0且a≠1)的反函数的图象
经过点(1, 4),求a的值.解:依题意,原函数经过点(4,1)得练3:
已知函数的图象过点(-2,1),则的图象必过哪个点?答:(1,-2)结论3:互为反函数的函数图象关于直线y=x对称。回顾总结反 函 数函数y=ax(a>0,且a≠1)与y=logax(a>0,且a≠1) 互为反函数两个函数都是一一映射两个函数的定义域值域互换两个函数图象关于直线
y=x对称两个函数的单调性一致
-2-100
1
22438-3
-2-10
02
142
83
在同一坐标系中作函数和函数的图像。问题2:
观察函数y=log2x与函数y=2x的图像,分析它们之间的关系.关于直线y=x对称同底的指数函数和对数函数的图象
的增长速度的差异有何差异?思 考都是增函数,但在第一象限指数函数增长速度越来越快,对数函数增长速度越来越慢。同底的指数函数与对数函数性质关系对照表 1.两个函数的图象关于直线
y = x对称.2.两个函数的定义域、值域互换.3.横、纵坐标互换.4.单调性一致.增函数减函数问题1:
指数函数y=ax与对数函数y=loga x(a>0,a≠1)有什么关系?称这两个函数互为反函数y=axx=loga yy=loga x指数换对数交换x,yy=3x+5交换x,y移项指数函数y=ax(a>0,a≠1)对数函数y=logax(a>0,a≠1)指数函数y=ax是对数函数y=loga x(a>0,a≠1)的反函数1.一一映射的函数才有反函数。
2.对数函数y=loga x与指数函数y=ax互为反函数。
3.互为反函数的图象关于直线y=x对称。
4.函数y=f(x)的反函数通常用y=f-1(x) 表示。
注意:y=f-1(x) 读作:“f逆x”
表示反函数,不是-1次幂(倒数)的意思例1 写出下列对数函数的反函数:
(1)y =lgx; 解(1)y=10x(2)x、y互换得反函数x、y互换得反函数例2 写出下列指数函数的反函数:
(1) y=5x 例3 求函数y=3x-2(x>0)反函数,并在同一直角坐标系中作出函数及其反函数的图象。解:由y=3x-2(x>0 )得 (y>-2 )所以y=3x-2(x∈R)的反函数是(x>-2 )y=3x-2 经过两点(0,-2), (2/3,0)做一做y=3x-2y=x求函数反函数的步骤:3? 求原函数的值域1? 反解2? x与y互换4? 写出反函数及它的定义域 练1:求下列函数的反函数:结论1:互为反函数的两个函数定义域、值域互换。解:练2:下列函数与练习1中的函数结论2:只有一一映射的函数才有反函数。有何异同?此函数是否有反函数?b=f(a)a=f-1(b)点(b,a)在反函数y=f-1(x) 的图像上点(a,b)在函数y=f(x)的图像上结论:[例4]函数f(x)=loga (x-1)(a>0且a≠1)的反函数的图象
经过点(1, 4),求a的值.解:依题意,原函数经过点(4,1)得练3:
已知函数的图象过点(-2,1),则的图象必过哪个点?答:(1,-2)结论3:互为反函数的函数图象关于直线y=x对称。回顾总结反 函 数函数y=ax(a>0,且a≠1)与y=logax(a>0,且a≠1) 互为反函数两个函数都是一一映射两个函数的定义域值域互换两个函数图象关于直线
y=x对称两个函数的单调性一致
