方程的根与函数的零点
图片预览






文档简介
课件45张PPT。2.4.1函数的零点预习检验问:
函数的零点是一个点(a,0)
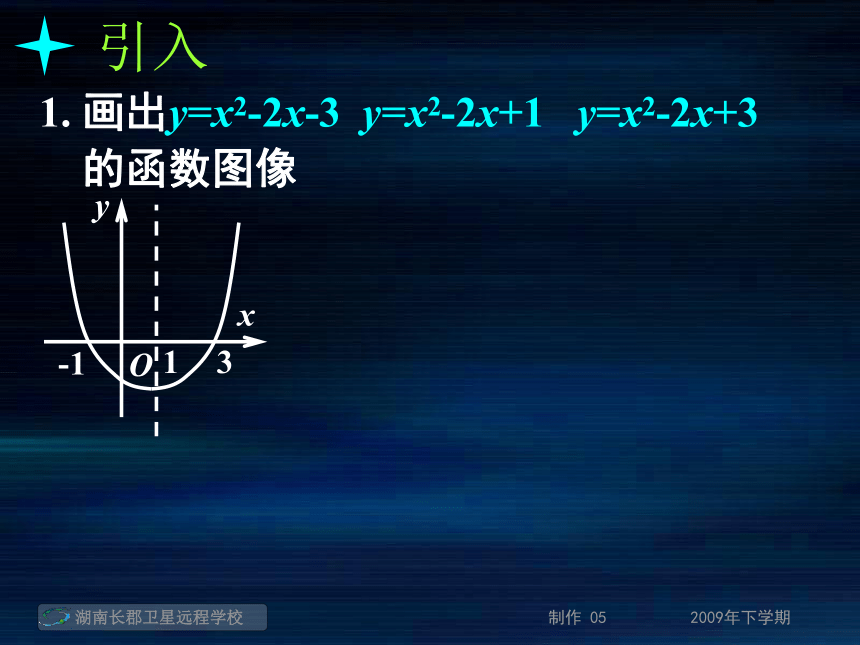
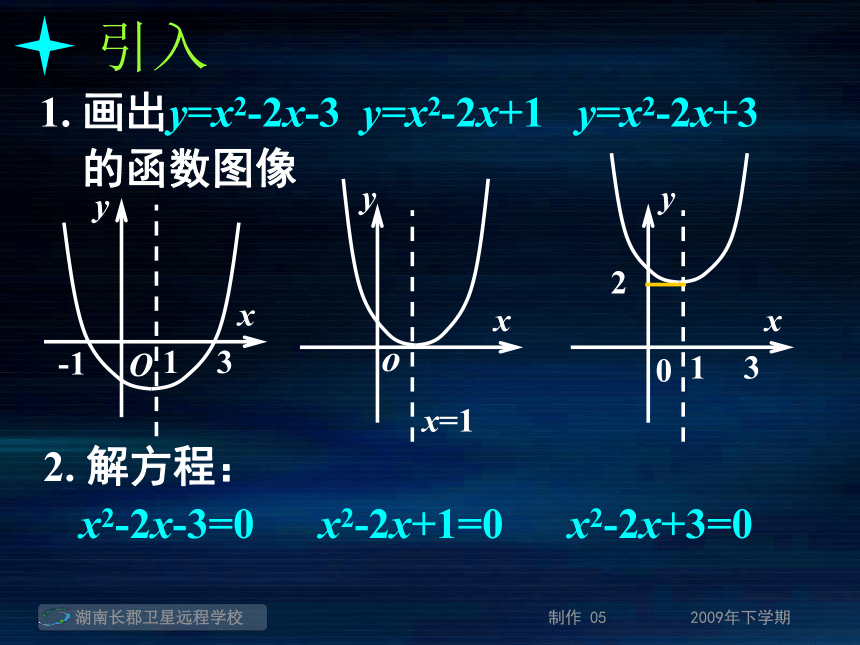
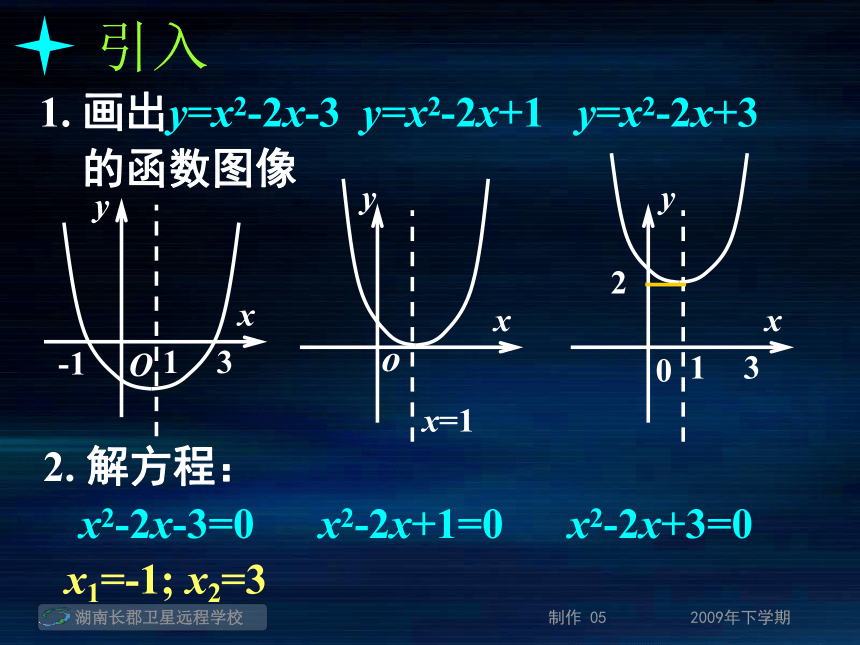
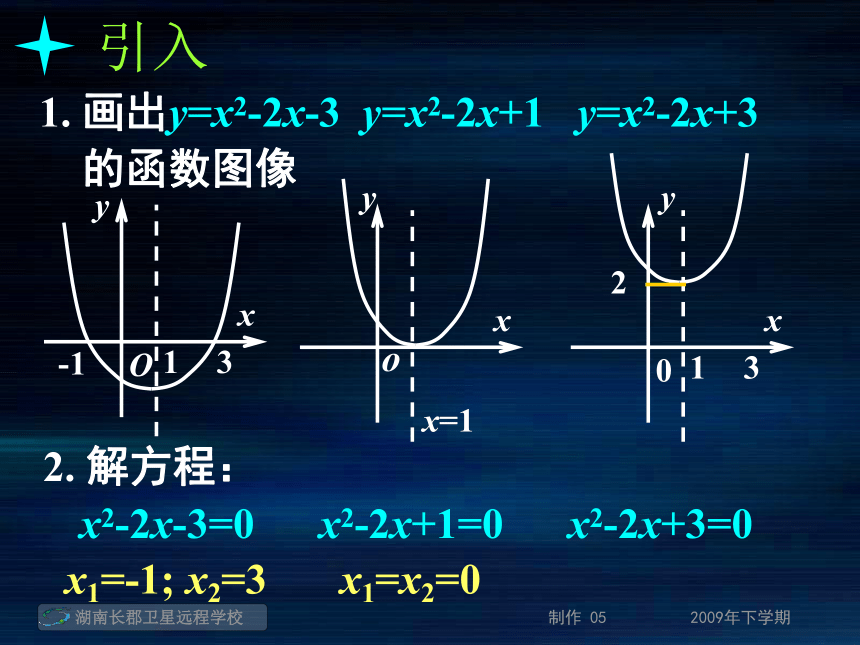
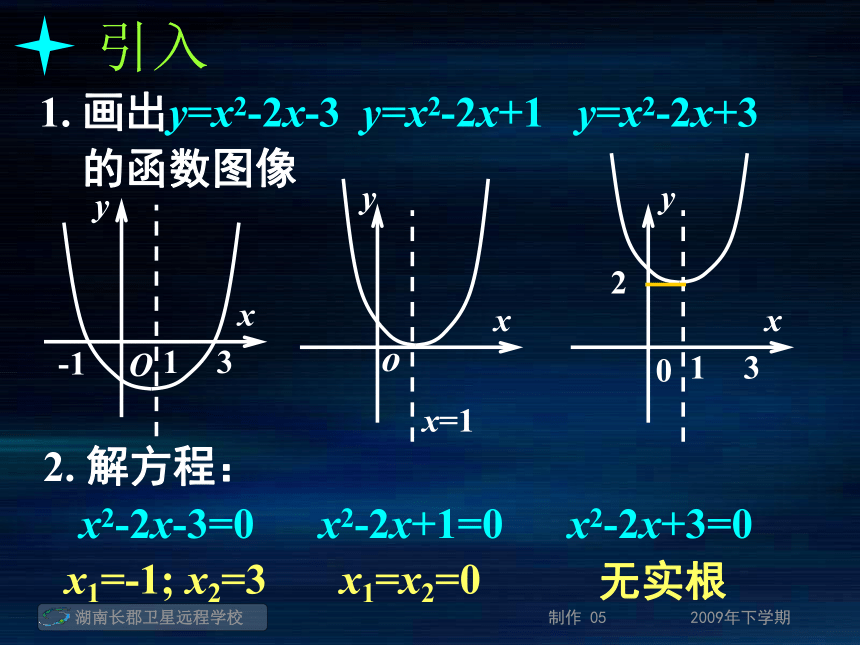
还是一个实数a?引入1. 画出y=x2-2x-3 y=x2-2x+1 y=x2-2x+3 的函数图像引入1. 画出y=x2-2x-3 y=x2-2x+1 y=x2-2x+3 的函数图像引入1. 画出y=x2-2x-3 y=x2-2x+1 y=x2-2x+3 的函数图像引入1. 画出y=x2-2x-3 y=x2-2x+1 y=x2-2x+3 的函数图像引入1. 画出y=x2-2x-3 y=x2-2x+1 y=x2-2x+3 的函数图像2. 解方程:x2-2x-3=0 x2-2x+1=0 x2-2x+3=0引入1. 画出y=x2-2x-3 y=x2-2x+1 y=x2-2x+3 的函数图像2. 解方程:x2-2x-3=0 x2-2x+1=0 x2-2x+3=0x1=-1; x2=3引入1. 画出y=x2-2x-3 y=x2-2x+1 y=x2-2x+3 的函数图像2. 解方程:x2-2x-3=0 x2-2x+1=0 x2-2x+3=0x1=-1; x2=3x1=x2=0引入1. 画出y=x2-2x-3 y=x2-2x+1 y=x2-2x+3 的函数图像2. 解方程:x2-2x-3=0 x2-2x+1=0 x2-2x+3=0x1=-1; x2=3x1=x2=0无实根方程 f(x)=0 有实数根方程 f(x)=0 有实数根函数y=f(x)的图象与x轴有交点方程 f(x)=0 有实数根函数y=f(x)的图象与x轴有交点函数y=f(x)有零点方程 f(x)=0 有实数根函数y=f(x)的图象与x轴有交点有实根x0函数y=f(x)有零点方程 f(x)=0 有实数根函数y=f(x)的图象与x轴有交点有实根x0函数y=f(x)有零点有交点(x0, 0)方程 f(x)=0 有实数根函数y=f(x)的图象与x轴有交点有实根x0函数y=f(x)有零点有交点(x0, 0) 零点:对于函数y=f(x), 我们把使f(x)=0的实数x叫做函数y=f(x)的零点。对零点的理解:对零点的理解:"数"的角度:对零点的理解:"数"的角度:即是使f(x)=0的实数x的值对零点的理解:"数"的角度:"形"的角度:即是使f(x)=0的实数x的值对零点的理解:"数"的角度:"形"的角度:即是使f(x)=0的实数x的值即是函数f(x)的图象与x轴的交点的横坐标对零点的理解:"数"的角度:"形"的角度:即是使f(x)=0的实数x的值即是函数f(x)的图象与x轴的交点的横坐标求函数零点的方法:对零点的理解:"数"的角度:"形"的角度:即是使f(x)=0的实数x的值即是函数f(x)的图象与x轴的交点的横坐标求函数零点的方法:(1) 方程法:对零点的理解:"数"的角度:"形"的角度:即是使f(x)=0的实数x的值即是函数f(x)的图象与x轴的交点的横坐标求函数零点的方法:(1) 方程法:解方程f(x)=0, 得到y=f(x)的零点对零点的理解:"数"的角度:"形"的角度:即是使f(x)=0的实数x的值即是函数f(x)的图象与x轴的交点的横坐标求函数零点的方法:(1) 方程法:(2) 图象法:解方程f(x)=0, 得到y=f(x)的零点对零点的理解:"数"的角度:"形"的角度:即是使f(x)=0的实数x的值即是函数f(x)的图象与x轴的交点的横坐标求函数零点的方法:(1) 方程法:(2) 图象法:解方程f(x)=0, 得到y=f(x)的零点画出函数y=f(x)的图象, 其图象与x轴交点的横坐标是函数y= f(x)的零点方程f(x)=0有实数根函数y=f(x)的图象与x轴有交点函数y=f(x)有零点等价关系:y=-x2-x+20; (2)y=2x-1; 例1:求下列函数的零点.求函数零点的步骤:
(1)令f(x)=0;
(2)解方程f(x)=0;
(3)写出零点练习1:求下列函数的零点:
(1) ;(2)y=x3-4x.
(3)y=-x2+6x+7;
求函数零点的步骤:
(1)令f(x)=0;
(2)解方程f(x)=0;
(3)写出零点 问题探究观察函数的图象
①在区间(a,b)上______(有/无)零点;f(a).f(b)_____0(<或>).
② 在区间(b,c)上______(有/无)零点;f(b).f(c) _____ 0(<或>).
③ 在区间(c,d)上______(有/无)零点;f(c).f(d) _____ 0(<或>).知识探究(二):函数零点存在性原理 -15-4<3<有<有<有<结论结论:零点存在定理函数零点的存在性定理 如果函数y=f(x)在区间[a, b]上的图象 是连续不断的一条曲线, 并且有f(a)·f(b)<0, 那么函数y=f(x)在区间(a, b)内必有零点, 即 存在c∈(a, b), 使得f(c)=0, 这个c也就是方程f(x)=0的根.对函数零点的存在性定理的理解对函数零点的存在性定理的理解 (1) 函数零点的存在性定理只能判断函数零点的存在性,不能判断零点的个数.对函数零点的存在性定理的理解 (1) 函数零点的存在性定理只能判断函数零点的存在性,不能判断零点的个数. (2) 只要函数y=f(x)在区间[a, b]上的图象连续不断,且在区间[a, b]两端的函数值异号, 则函数y=f(x)在区间[a, b]上必定存在零点.对函数零点的存在性定理的理解 (1) 函数零点的存在性定理只能判断函数零点的存在性,不能判断零点的个数. (2) 只要函数y=f(x)在区间[a, b]上的图象连续不断,且在区间[a, b]两端的函数值异号, 则函数y=f(x)在区间[a, b]上必定存在零点. (3) 若函数y=f(x)在区间[a, b]上的图象连续不断, 且函数y=f(x)在区间[a, b]也存在零点, 则函数y=f(x)在区间[a, b]两端的函数值可能同号也可能异号.思考:若函数y=f(x) 在区间(a, b)内有零点,一定能得出f(a)·f(b)<0的结论吗? 结论例如果函数 y=f(x) 在[a,b]上,图象是连续的,并且在闭区间的两个端点上的函数值互异即f(a)f(b)﹤0,且是单调函数,那么这个函数在(a,b)内必有惟一的一个零点。利用函数零点的存在性定理求函数零点的步骤利用函数零点的存在性定理求函数零点的步骤(1) 确定函数y=f(x)在[a, b]上连续;利用函数零点的存在性定理求函数零点的步骤(1) 确定函数y=f(x)在[a, b]上连续;(2) 若f(a)·f(b)<0, 则在(a, b)内存在零点.利用函数零点的存在性定理求函数零点的步骤(1) 确定函数y=f(x)在[a, b]上连续;(2) 若f(a)·f(b)<0, 则在(a, b)内存在零点.(3) 存在c∈(a, b), 使得f(c)=0, 则c是零点.例2:已知函数y=f(x)在区间[a,b]上是连续不断的曲线,判断下列结论,正确的是_________.(5)练习2:在下列哪个区间内,函数f(x)= x3+3x-5
一定有零点( )
A、(-1,0) B、(0,1)
C、(1,2) D、(2,3)C B 对于函数y=f(x), 叫做函数
y=f(x)的零点。方程f(x)=0有实数根函数的零点定义:等价关系使f(x)=0的实数x零点的求法 代数法图像法
小 结
函数的零点是一个点(a,0)
还是一个实数a?引入1. 画出y=x2-2x-3 y=x2-2x+1 y=x2-2x+3 的函数图像引入1. 画出y=x2-2x-3 y=x2-2x+1 y=x2-2x+3 的函数图像引入1. 画出y=x2-2x-3 y=x2-2x+1 y=x2-2x+3 的函数图像引入1. 画出y=x2-2x-3 y=x2-2x+1 y=x2-2x+3 的函数图像引入1. 画出y=x2-2x-3 y=x2-2x+1 y=x2-2x+3 的函数图像2. 解方程:x2-2x-3=0 x2-2x+1=0 x2-2x+3=0引入1. 画出y=x2-2x-3 y=x2-2x+1 y=x2-2x+3 的函数图像2. 解方程:x2-2x-3=0 x2-2x+1=0 x2-2x+3=0x1=-1; x2=3引入1. 画出y=x2-2x-3 y=x2-2x+1 y=x2-2x+3 的函数图像2. 解方程:x2-2x-3=0 x2-2x+1=0 x2-2x+3=0x1=-1; x2=3x1=x2=0引入1. 画出y=x2-2x-3 y=x2-2x+1 y=x2-2x+3 的函数图像2. 解方程:x2-2x-3=0 x2-2x+1=0 x2-2x+3=0x1=-1; x2=3x1=x2=0无实根方程 f(x)=0 有实数根方程 f(x)=0 有实数根函数y=f(x)的图象与x轴有交点方程 f(x)=0 有实数根函数y=f(x)的图象与x轴有交点函数y=f(x)有零点方程 f(x)=0 有实数根函数y=f(x)的图象与x轴有交点有实根x0函数y=f(x)有零点方程 f(x)=0 有实数根函数y=f(x)的图象与x轴有交点有实根x0函数y=f(x)有零点有交点(x0, 0)方程 f(x)=0 有实数根函数y=f(x)的图象与x轴有交点有实根x0函数y=f(x)有零点有交点(x0, 0) 零点:对于函数y=f(x), 我们把使f(x)=0的实数x叫做函数y=f(x)的零点。对零点的理解:对零点的理解:"数"的角度:对零点的理解:"数"的角度:即是使f(x)=0的实数x的值对零点的理解:"数"的角度:"形"的角度:即是使f(x)=0的实数x的值对零点的理解:"数"的角度:"形"的角度:即是使f(x)=0的实数x的值即是函数f(x)的图象与x轴的交点的横坐标对零点的理解:"数"的角度:"形"的角度:即是使f(x)=0的实数x的值即是函数f(x)的图象与x轴的交点的横坐标求函数零点的方法:对零点的理解:"数"的角度:"形"的角度:即是使f(x)=0的实数x的值即是函数f(x)的图象与x轴的交点的横坐标求函数零点的方法:(1) 方程法:对零点的理解:"数"的角度:"形"的角度:即是使f(x)=0的实数x的值即是函数f(x)的图象与x轴的交点的横坐标求函数零点的方法:(1) 方程法:解方程f(x)=0, 得到y=f(x)的零点对零点的理解:"数"的角度:"形"的角度:即是使f(x)=0的实数x的值即是函数f(x)的图象与x轴的交点的横坐标求函数零点的方法:(1) 方程法:(2) 图象法:解方程f(x)=0, 得到y=f(x)的零点对零点的理解:"数"的角度:"形"的角度:即是使f(x)=0的实数x的值即是函数f(x)的图象与x轴的交点的横坐标求函数零点的方法:(1) 方程法:(2) 图象法:解方程f(x)=0, 得到y=f(x)的零点画出函数y=f(x)的图象, 其图象与x轴交点的横坐标是函数y= f(x)的零点方程f(x)=0有实数根函数y=f(x)的图象与x轴有交点函数y=f(x)有零点等价关系:y=-x2-x+20; (2)y=2x-1; 例1:求下列函数的零点.求函数零点的步骤:
(1)令f(x)=0;
(2)解方程f(x)=0;
(3)写出零点练习1:求下列函数的零点:
(1) ;(2)y=x3-4x.
(3)y=-x2+6x+7;
求函数零点的步骤:
(1)令f(x)=0;
(2)解方程f(x)=0;
(3)写出零点 问题探究观察函数的图象
①在区间(a,b)上______(有/无)零点;f(a).f(b)_____0(<或>).
② 在区间(b,c)上______(有/无)零点;f(b).f(c) _____ 0(<或>).
③ 在区间(c,d)上______(有/无)零点;f(c).f(d) _____ 0(<或>).知识探究(二):函数零点存在性原理 -15-4<3<有<有<有<结论结论:零点存在定理函数零点的存在性定理 如果函数y=f(x)在区间[a, b]上的图象 是连续不断的一条曲线, 并且有f(a)·f(b)<0, 那么函数y=f(x)在区间(a, b)内必有零点, 即 存在c∈(a, b), 使得f(c)=0, 这个c也就是方程f(x)=0的根.对函数零点的存在性定理的理解对函数零点的存在性定理的理解 (1) 函数零点的存在性定理只能判断函数零点的存在性,不能判断零点的个数.对函数零点的存在性定理的理解 (1) 函数零点的存在性定理只能判断函数零点的存在性,不能判断零点的个数. (2) 只要函数y=f(x)在区间[a, b]上的图象连续不断,且在区间[a, b]两端的函数值异号, 则函数y=f(x)在区间[a, b]上必定存在零点.对函数零点的存在性定理的理解 (1) 函数零点的存在性定理只能判断函数零点的存在性,不能判断零点的个数. (2) 只要函数y=f(x)在区间[a, b]上的图象连续不断,且在区间[a, b]两端的函数值异号, 则函数y=f(x)在区间[a, b]上必定存在零点. (3) 若函数y=f(x)在区间[a, b]上的图象连续不断, 且函数y=f(x)在区间[a, b]也存在零点, 则函数y=f(x)在区间[a, b]两端的函数值可能同号也可能异号.思考:若函数y=f(x) 在区间(a, b)内有零点,一定能得出f(a)·f(b)<0的结论吗? 结论例如果函数 y=f(x) 在[a,b]上,图象是连续的,并且在闭区间的两个端点上的函数值互异即f(a)f(b)﹤0,且是单调函数,那么这个函数在(a,b)内必有惟一的一个零点。利用函数零点的存在性定理求函数零点的步骤利用函数零点的存在性定理求函数零点的步骤(1) 确定函数y=f(x)在[a, b]上连续;利用函数零点的存在性定理求函数零点的步骤(1) 确定函数y=f(x)在[a, b]上连续;(2) 若f(a)·f(b)<0, 则在(a, b)内存在零点.利用函数零点的存在性定理求函数零点的步骤(1) 确定函数y=f(x)在[a, b]上连续;(2) 若f(a)·f(b)<0, 则在(a, b)内存在零点.(3) 存在c∈(a, b), 使得f(c)=0, 则c是零点.例2:已知函数y=f(x)在区间[a,b]上是连续不断的曲线,判断下列结论,正确的是_________.(5)练习2:在下列哪个区间内,函数f(x)= x3+3x-5
一定有零点( )
A、(-1,0) B、(0,1)
C、(1,2) D、(2,3)C B 对于函数y=f(x), 叫做函数
y=f(x)的零点。方程f(x)=0有实数根函数的零点定义:等价关系使f(x)=0的实数x零点的求法 代数法图像法
小 结
