7.1.2角平分线、中线、高线
文档属性
| 名称 | 7.1.2角平分线、中线、高线 |  | |
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-01-07 14:11:59 | ||
图片预览








文档简介
课件30张PPT。 一.教材分析:《数学课程标准》对这部分的要求;了解三角形相关的概念,(中线、高、角平分线),会画出任意三角形的角平分线、中线和高,了解三角形的稳定性.
教材的地位与作用:
《三角形的高、中线与角平分线》是初等数学的基础知识,也是进一步学习几何知识的基础,为以后认识和学习几何知识奠定基础,是学生体会数学价值观,增强审美意识的重要题材,所以学会《三角形的高、中线与角平分线》是致关重要的。二.教学目标 1.经历析纸,画图及教师展示课件等过程认识三角形的高、中线与角平分线. ??? 2.会用工具准确画出三角形的高、中线与角平分线, 通过画图了解三角形 的三条高(及所在直线)交于一点,三角形的三条中线,三条角平分线等都交于点 重难点 重点: ? (1)了解三角形的高、中线与角平分线的概念, 会用工具准确画出三角形的高、中线与角平分线. ??? (2)了解三角形的三条高、三条中线与三条角平分线分别交于一点.
.难点: ? (1)三角形平分线与角平分线的区别,三角形的高与垂线的区别. ? (2)钝角三角形高的画法. ? (3)不同的三角形三条高的位置关系三.教学方法,教学手段的选择
让学生参与知识的形成过程,改变传统教材“给出法则,让学生模仿学习”的框架,在学习《三角形的高、中线与角平分线》的教学中,打破常规,在学生自己发现的基础上,鼓励学生自己探究,让学生自己归纳,自己总结,体现课程标准所提出的,注重知识间的联系,注重学生能力的培养的要求。
整节课采取学生自己探究,自己发现来落实知识点,利用多媒体课件充分提高了课堂教学的效率,激发学生的学习积极性。学情分析:
七年级的学生在小学也认识了一些图形,有过认识图形的体验,但很不系统,这个年级的学生思维活跃,学习图形对培养学生学习数学的兴趣和审美能力有很大帮助。学法指导:
1.鼓励学生步步为营,及时指导学生在学习中出现的错误,让他们克服马虎的习惯。
2.学习图形利用了声光影像完备的多媒体课件,增强了学生的视觉感,引发他们的兴趣。
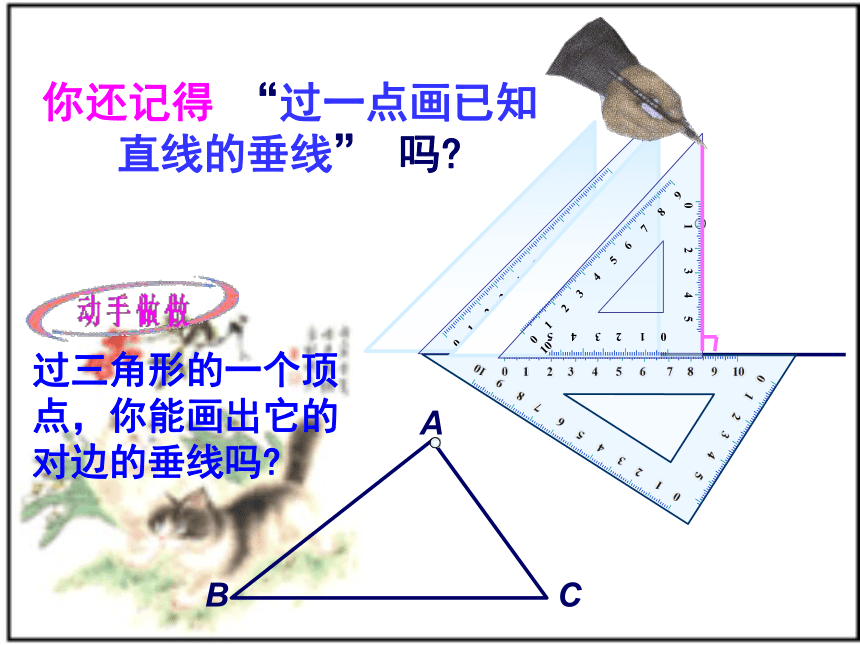
3.学习新知识教师引导,学生自己探究,自己发现,自己归纳总结,增强学生的成就感和自信心,从而培养他们对数学的热爱。你还记得 “过一点画已知
直线的垂线” 吗?三角形的高A从三角形的一个顶点BC向它的对边所在直线作垂线,顶点和垂足之间的线段叫做三角形这边的高,简称三角形的高。如图, 线段AD是BC边上的高. 任意画一个锐角△ABC,和垂足的字母.请你画出BC边上的高.锐角三角形的三条高 每人画一个锐角三角形。
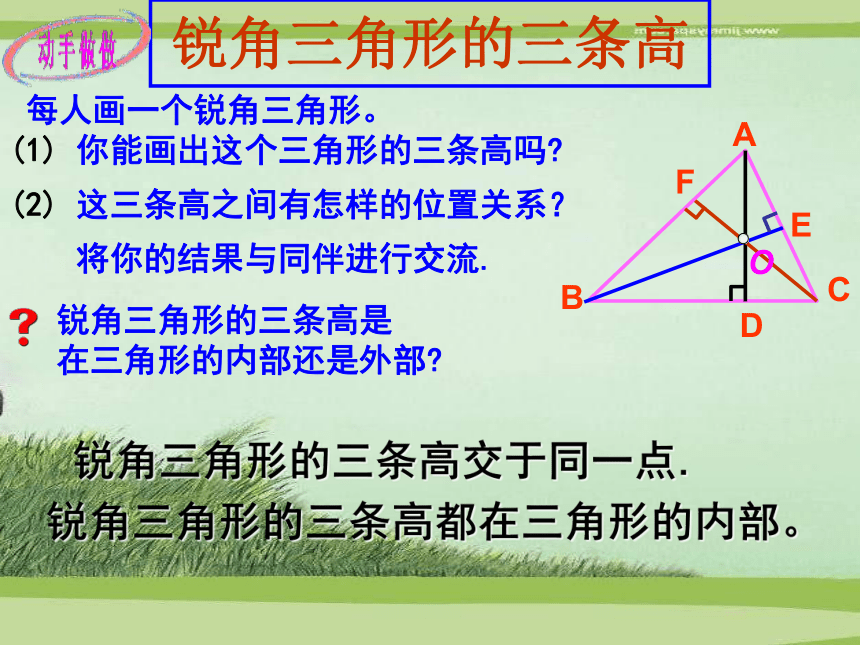
(1) 你能画出这个三角形的三条高吗?(2) 这三条高之间有怎样的位置关系? 将你的结果与同伴进行交流.锐角三角形的三条高是
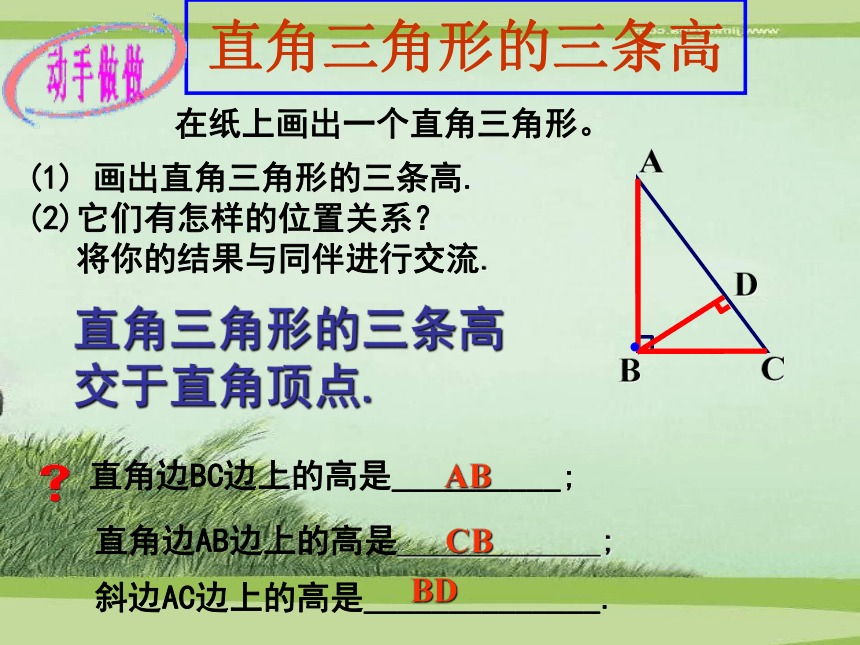
在三角形的内部还是外部?ABCDEF锐角三角形的三条高交于同一点.锐角三角形的三条高都在三角形的内部。直角三角形的三条高在纸上画出一个直角三角形。 将你的结果与同伴进行交流.ABC(1) 画出直角三角形的三条高.直角边BC边上的高是__________; AB直角边AB边上的高是 ;CB(2)它们有怎样的位置关系?D斜边AC边上的高是______________. BD●直角三角形的三条高
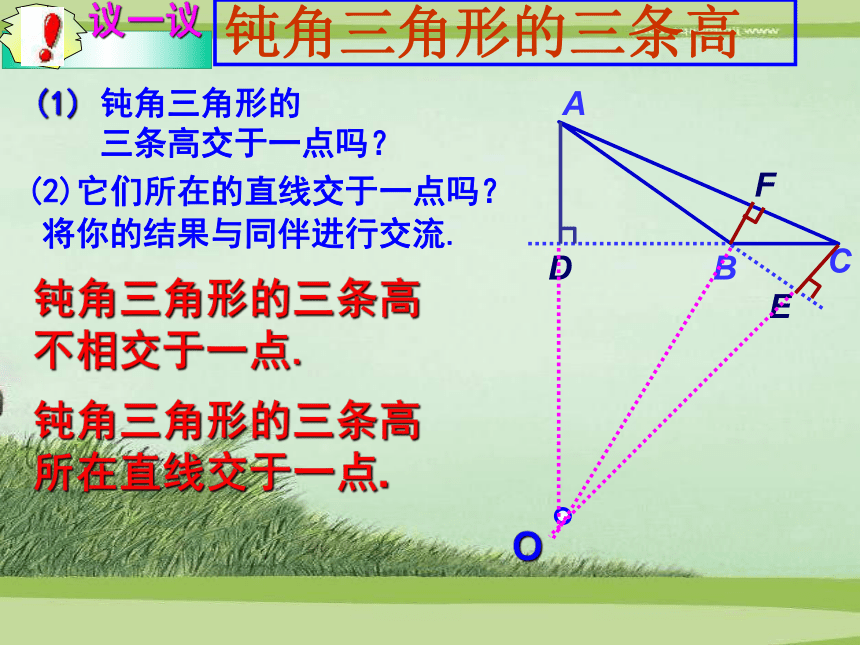
交于直角顶点.钝角三角形的三条高(1) 钝角三角形的
三条高交于一点吗?(2)它们所在的直线交于一点吗?将你的结果与同伴进行交流.O钝角三角形的三条高
不相交于一点.钝角三角形的三条高
所在直线交于一点.小结:三角形的高从三角形中的一个顶点向它的对边所在直线作垂线,顶点和垂足之间的线段 叫做三角形这边的高。311相交相交不相交相交相交相交三角形的三条高所在直线交于一点三角形内部直角顶点三角形外部三角形的中线在三角形中,连接一个顶点与它对边中点的线段,叫做这个三角形这边的中线.D∵AD是△ ABC的中线
任意画一个三角形,然后利用刻度尺画出
这个三角形三条边的中线,你发现了什么?●●三角形的三条中线相交于一点,交点在三角形的内部.三角形中线的理解EFO也就是说:三角形的任意一条中线把这个
三角形分成了两个面积相等的三角形。
如右图
∵D是BC的中点
∴BD=DC
而△ABD的面积= BD×AE
△ADC的面积= DC×AE
故△ABD的面积= △ADC的面积三角形的角平分线叫做三角形的角平分线。ABCD∵AD是 △ ABC的角平分线
任意画一个三角形,然后利用量角器画出
这个三角形三个角的角平分线,你发现了什么?●●在三角形中,一个内角的角平分线与它的对边相交,这个角的顶点与交点之间的线段,三角形的三条角平分线相交于一点,交点在三角形的内部ACBFEDO∵BE是△ABC的角平分线∴____=_____= _____∴∠ACB=2______=2______∠ABE∠CBE∠ABC∠ACF∵CF是△ABC的角平分线∠BCF 三角形的角平分线与角的 平分线有什么区别?思考三角形的角平分线是一条线段 , 角的平分线是一条射线.角平分线的理解课堂练习2.如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是( )A.锐角三角形 B.直角三角形
C.钝角三角形 D.都对BD分析(1)△ABD的周长=AB+AD+BD
△ACD的周长=AC+AD+DC
△ABD的周长与△ACD的周长之差
= (AB+AD+BD)-(AC+AD+DC)
而BD=CD.所以上式=AB-AC=5-3=2
(2) △ABD= BD×AE
而BD=DC
△ACD= DC×AEA例二如下图,在△ABC中,∠1=∠2,G为
AD的中点,延长BG交AC于E,F为
AB上一点,CF⊥AD于H,下面判断
正确的有( )①AD是△ABE的角平分线;
例二如下图,在△ABC中,∠1=∠2,G为
AD的中点,延长BG交AC于E,F为
AB上一点,CF⊥AD于H,下面判断
正确的有( )②BE是△ABD边AD上的中线;
例二如下图,在△ABC中,∠1=∠2,G为
AD的中点,延长BG交AC于E,F为
AB上一点,CF⊥AD于H,下面判断
正确的有( )③CH为△ACD边AD上的高。例二如下图,在△ABC中,∠1=∠2,G为
AD的中点,延长BG交AC于E,F为
AB上一点,CF⊥AD于H,下面判断
正确的有( )③CH为△ACD边AD上的高。感悟与反思通过这节课的学习你有哪些收获?
你还有什么想法吗?3、 4。作 业p69页7.1练习拓展AFCDAC∠2 ∠ABC∠4拓展练习CEBC∠CAD∠BAC∠AFC4.填空:如图,在ΔABC中,AE是中线,AD是角平分线,AF是高。
(1)BE= = ;
(2)∠BAD= = ;
(3)∠AFB= = 90°拓展练习5.如图1所示,在△ABC中,∠ACB=90°,把△ABC沿直线AC翻折180°,使点B 落在点B′的位置,则线段AC具有性质( )
A.是边BB′上的中线 B.是边BB′上的高
C.是∠BAB′的角平分线 D.以上三种性质合一
D拓展练习6.如图2所示,D,E分别是△ABC的边AC,BC的中点,则下列说法不正确的是( )
A.DE是△BCD的中线 B.BD是△ABC的中线
C.AD=DC,BD=EC D.∠C的对边是DE
C
教材的地位与作用:
《三角形的高、中线与角平分线》是初等数学的基础知识,也是进一步学习几何知识的基础,为以后认识和学习几何知识奠定基础,是学生体会数学价值观,增强审美意识的重要题材,所以学会《三角形的高、中线与角平分线》是致关重要的。二.教学目标 1.经历析纸,画图及教师展示课件等过程认识三角形的高、中线与角平分线. ??? 2.会用工具准确画出三角形的高、中线与角平分线, 通过画图了解三角形 的三条高(及所在直线)交于一点,三角形的三条中线,三条角平分线等都交于点 重难点 重点: ? (1)了解三角形的高、中线与角平分线的概念, 会用工具准确画出三角形的高、中线与角平分线. ??? (2)了解三角形的三条高、三条中线与三条角平分线分别交于一点.
.难点: ? (1)三角形平分线与角平分线的区别,三角形的高与垂线的区别. ? (2)钝角三角形高的画法. ? (3)不同的三角形三条高的位置关系三.教学方法,教学手段的选择
让学生参与知识的形成过程,改变传统教材“给出法则,让学生模仿学习”的框架,在学习《三角形的高、中线与角平分线》的教学中,打破常规,在学生自己发现的基础上,鼓励学生自己探究,让学生自己归纳,自己总结,体现课程标准所提出的,注重知识间的联系,注重学生能力的培养的要求。
整节课采取学生自己探究,自己发现来落实知识点,利用多媒体课件充分提高了课堂教学的效率,激发学生的学习积极性。学情分析:
七年级的学生在小学也认识了一些图形,有过认识图形的体验,但很不系统,这个年级的学生思维活跃,学习图形对培养学生学习数学的兴趣和审美能力有很大帮助。学法指导:
1.鼓励学生步步为营,及时指导学生在学习中出现的错误,让他们克服马虎的习惯。
2.学习图形利用了声光影像完备的多媒体课件,增强了学生的视觉感,引发他们的兴趣。
3.学习新知识教师引导,学生自己探究,自己发现,自己归纳总结,增强学生的成就感和自信心,从而培养他们对数学的热爱。你还记得 “过一点画已知
直线的垂线” 吗?三角形的高A从三角形的一个顶点BC向它的对边所在直线作垂线,顶点和垂足之间的线段叫做三角形这边的高,简称三角形的高。如图, 线段AD是BC边上的高. 任意画一个锐角△ABC,和垂足的字母.请你画出BC边上的高.锐角三角形的三条高 每人画一个锐角三角形。
(1) 你能画出这个三角形的三条高吗?(2) 这三条高之间有怎样的位置关系? 将你的结果与同伴进行交流.锐角三角形的三条高是
在三角形的内部还是外部?ABCDEF锐角三角形的三条高交于同一点.锐角三角形的三条高都在三角形的内部。直角三角形的三条高在纸上画出一个直角三角形。 将你的结果与同伴进行交流.ABC(1) 画出直角三角形的三条高.直角边BC边上的高是__________; AB直角边AB边上的高是 ;CB(2)它们有怎样的位置关系?D斜边AC边上的高是______________. BD●直角三角形的三条高
交于直角顶点.钝角三角形的三条高(1) 钝角三角形的
三条高交于一点吗?(2)它们所在的直线交于一点吗?将你的结果与同伴进行交流.O钝角三角形的三条高
不相交于一点.钝角三角形的三条高
所在直线交于一点.小结:三角形的高从三角形中的一个顶点向它的对边所在直线作垂线,顶点和垂足之间的线段 叫做三角形这边的高。311相交相交不相交相交相交相交三角形的三条高所在直线交于一点三角形内部直角顶点三角形外部三角形的中线在三角形中,连接一个顶点与它对边中点的线段,叫做这个三角形这边的中线.D∵AD是△ ABC的中线
任意画一个三角形,然后利用刻度尺画出
这个三角形三条边的中线,你发现了什么?●●三角形的三条中线相交于一点,交点在三角形的内部.三角形中线的理解EFO也就是说:三角形的任意一条中线把这个
三角形分成了两个面积相等的三角形。
如右图
∵D是BC的中点
∴BD=DC
而△ABD的面积= BD×AE
△ADC的面积= DC×AE
故△ABD的面积= △ADC的面积三角形的角平分线叫做三角形的角平分线。ABCD∵AD是 △ ABC的角平分线
任意画一个三角形,然后利用量角器画出
这个三角形三个角的角平分线,你发现了什么?●●在三角形中,一个内角的角平分线与它的对边相交,这个角的顶点与交点之间的线段,三角形的三条角平分线相交于一点,交点在三角形的内部ACBFEDO∵BE是△ABC的角平分线∴____=_____= _____∴∠ACB=2______=2______∠ABE∠CBE∠ABC∠ACF∵CF是△ABC的角平分线∠BCF 三角形的角平分线与角的 平分线有什么区别?思考三角形的角平分线是一条线段 , 角的平分线是一条射线.角平分线的理解课堂练习2.如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是( )A.锐角三角形 B.直角三角形
C.钝角三角形 D.都对BD分析(1)△ABD的周长=AB+AD+BD
△ACD的周长=AC+AD+DC
△ABD的周长与△ACD的周长之差
= (AB+AD+BD)-(AC+AD+DC)
而BD=CD.所以上式=AB-AC=5-3=2
(2) △ABD= BD×AE
而BD=DC
△ACD= DC×AEA例二如下图,在△ABC中,∠1=∠2,G为
AD的中点,延长BG交AC于E,F为
AB上一点,CF⊥AD于H,下面判断
正确的有( )①AD是△ABE的角平分线;
例二如下图,在△ABC中,∠1=∠2,G为
AD的中点,延长BG交AC于E,F为
AB上一点,CF⊥AD于H,下面判断
正确的有( )②BE是△ABD边AD上的中线;
例二如下图,在△ABC中,∠1=∠2,G为
AD的中点,延长BG交AC于E,F为
AB上一点,CF⊥AD于H,下面判断
正确的有( )③CH为△ACD边AD上的高。例二如下图,在△ABC中,∠1=∠2,G为
AD的中点,延长BG交AC于E,F为
AB上一点,CF⊥AD于H,下面判断
正确的有( )③CH为△ACD边AD上的高。感悟与反思通过这节课的学习你有哪些收获?
你还有什么想法吗?3、 4。作 业p69页7.1练习拓展AFCDAC∠2 ∠ABC∠4拓展练习CEBC∠CAD∠BAC∠AFC4.填空:如图,在ΔABC中,AE是中线,AD是角平分线,AF是高。
(1)BE= = ;
(2)∠BAD= = ;
(3)∠AFB= = 90°拓展练习5.如图1所示,在△ABC中,∠ACB=90°,把△ABC沿直线AC翻折180°,使点B 落在点B′的位置,则线段AC具有性质( )
A.是边BB′上的中线 B.是边BB′上的高
C.是∠BAB′的角平分线 D.以上三种性质合一
D拓展练习6.如图2所示,D,E分别是△ABC的边AC,BC的中点,则下列说法不正确的是( )
A.DE是△BCD的中线 B.BD是△ABC的中线
C.AD=DC,BD=EC D.∠C的对边是DE
C
