7.2.1三角形的内角
图片预览






文档简介
课件23张PPT。7.2.1三角形的内角www.1230.org 初中数学资源网 一、说教材1、教材的地位和作用 三角形是最常见的几何图形之一, 在工农业生产和日常生活中都有广泛的应用, 又因为三角形是多边形 的一种,而且是最简单的多边形,在几何里,常把多边形分割成若干个三角形,利用三角形的性质去研究多 边形,因此对三角形性质的研究显得十分重要。 在小学已学过三角形的内角的有关知识,知道三角形的内角和为 1800,但是为什么是 1800 并没有进行 研究,因此本节是在学生前几学段学过三角形、线段、角等,初步了解了一些简单几何体和平面图形及特征 会进行简单说理后,对“三角形的内角和定理”进行证明及简单应用。在证明过程中,通过一题多解,初步体 会思维的多向性,引导学生的个性化发展,通过本节学习可以进一步丰富对图形的认识和感受。 www.1230.org 初中数学资源网 2、学情分析七年级学生年龄较小, 思维正处在具体形象思维向抽象逻辑思维转变的阶段, 也是由代数运算向几何推 理过渡的较好时期,通过前面的学习,学生已具备一些分析问题、解决问题的能力,这样可以让学生和谐地 融入到探究性学习的氛围中。 3、教学目标 【知识与技能】探究并掌握三角形内角和等于 180°,并能应用三角形内角和性质解决一些简单的实际 问题。会用平行线的性质与平角的定义证明三角形的内角和等于 180° www.1230.org 初中数学资源网 【过程与方法】经历拼图实验、合作交流、推理论证的过程,发展空间观念、推理能力和有条理的表达 能力。 【情感态度价值观】学会多角度寻求解决问题的途径,在操作中进行自觉思考,积累数学探索的经验。 4、教学重难点 教学重点:三角形内角和定理的理解及其简单应用。 教学难点:三角形内角和定理的推理的过程以及辅助线的作法。 教学关键:利用平行线的性质推理证明三角形的内角和定理。 www.1230.org 初中数学资源网 二、说教法与学法1、教法分析 新课程标准的基本理念就是要让学生“人人学有价值的数学” 。强调“教学要从学生已有的经验出发, 让学生亲身经历将实际问题抽象成数学模型并进行解释与应用的过程。 而教师只是学生学习的组织者、 引导
者和合作者,在全面参与和了解学生的学习过程中起着对学生进行积极的评价,关注他们的学习方法、学习 水平和情感态度,促使学生向着预定的目标发展的作用” 因此,我采用了“动手操作—观察实验—猜想论 证—应用与拓展”的探究式教学方法来实施教学。 2、学法指导 依据新课程标准的要求,学习活动应体现学生身心发展特点,应有利于引导学生主动探索和发现,基于 本节课内容的特点,我将让学生通过动手实验、大胆猜想、自主探索,合作交流的学习方法,培养他们利用 旧知识获取新知识的能力,同时也培养学生探索能力和创新精神。 在一个直角三角形里住着三个内角,平时,它们三兄弟非常团结。可是有一天,老二突然不高兴,发起脾气来,它指着老大说:“你凭什么度数最大,我也要和你一样大!”“不行啊!”老大说:“这是不可能的,否则,我们这个家就再也围不起来了……”“为什么?” 老二很纳闷。
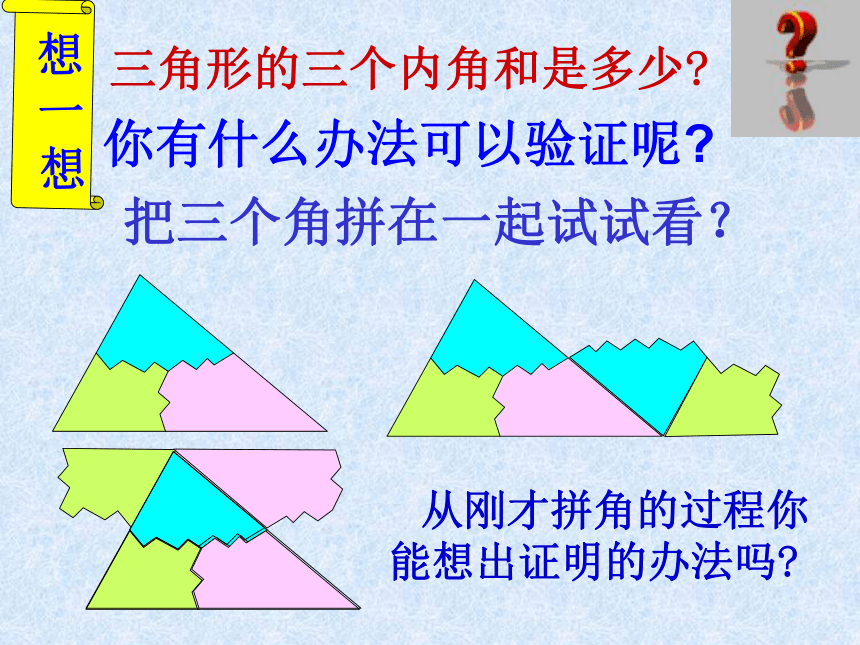
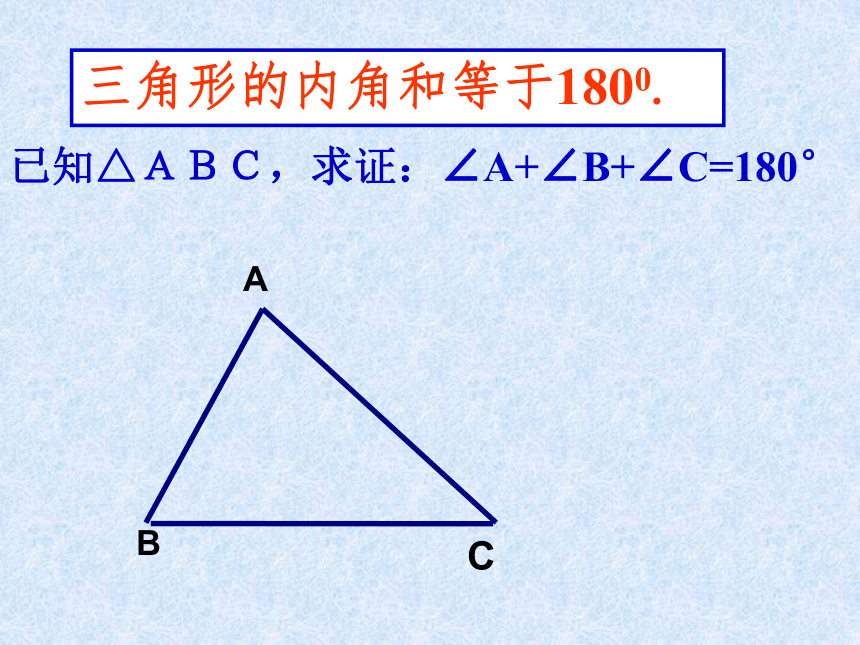
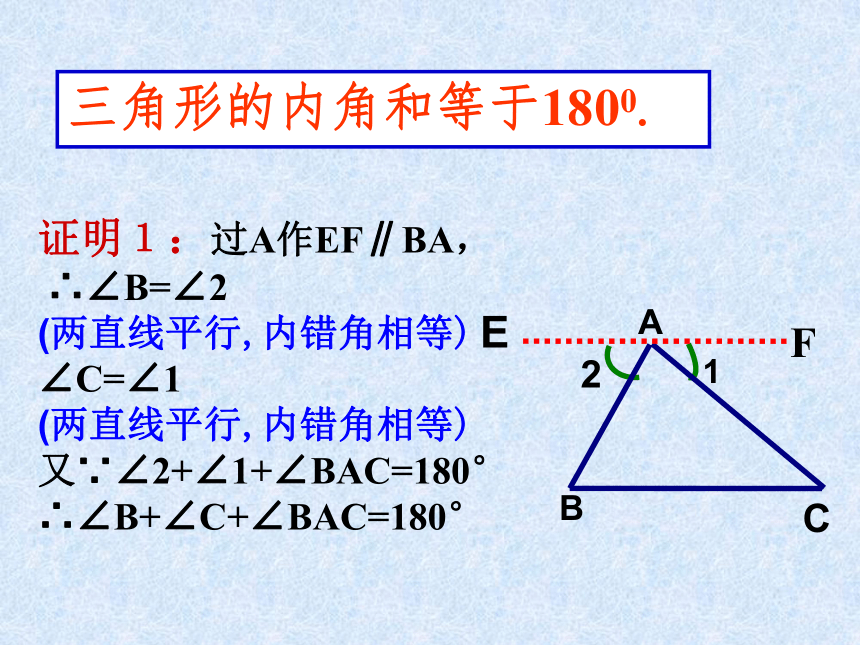
同学们,你们知道其中的道理吗?内角三兄弟之争三角形的三个内角和是多少?把三个角拼在一起试试看?你有什么办法可以验证呢? 从刚才拼角的过程你能想出证明的办法吗?三角形的内角和等于1800.已知△ABC,求证:∠A+∠B+∠C=180°证明1:过A作EF∥BA,
∴∠B=∠2
(两直线平行,内错角相等)
∠C=∠1
(两直线平行,内错角相等)
又∵∠2+∠1+∠BAC=180°
∴∠B+∠C+∠BAC=180°F21ECBA三角形的内角和等于1800.为什么要证明 按照上面的方法,已经可以验证三角形的内角和是180°,但是由于形状不同的三角形有无数多个,我们不可能通过上面的办法一一验证.再加上其验证过程中可能存在误差,不能保证其有效性.所以我们需要一种能证明任意一个三角形的内角和等于180°的方法.这个方法就是—证明.
一个命题是否正确,需要经过使人信服的推理论证才能得出结论.而证明是由命题的题设(已知)出发,经过严密的推理,最后推出结论(求证)正确的过程. 在这里,为了证明的需要,在原来的图形上添画的线叫做辅助线。在平面几何里,辅助线通常画成虚线。返回证明2:延长BC到D,过C作CE∥BA,
∴ ∠A=∠1
(两直线平行,内错角相等)
∠B=∠2
(两直线平行,同位角相等)
又∵∠1+∠2+∠ACB=180°
∴∠A+∠B+∠ACB=180°三角形的内角和等于1800.证明3:过A作AE∥BC,
∴∠B=∠BAE
(两直线平行,内错角相等)
∠EAB+∠BAC+∠C=180°
(两直线平行,同旁内角互补)
∴∠B+∠C+∠BAC=180°三角形的内角和等于1800.思路总结 为了证明三个角的和为1800,转化为一个平角或同旁内角互补,这种转化思想是数学中的常用方法.82 °新知应用 (1)在△ABC中,∠A=55°,∠ B=43 °
则∠A CB= . ∠ ACD=___
(2)在△ABC中,∠A=80°,∠B=∠C , 则∠C=______度。
(3)在直角三角形ABC中,一个锐角为40 °,则另一个锐角是_______度。98°50 50(4) 在△ABC中, ∠A :∠B:∠C=2:3:4,
求∠A 、∠B、 ∠C的度数。
解:设每一份角为X度,则∠A=2X 度、∠B=3X度、 ∠C=4X度,由三角形内角和定理,可得:
2X+3X+4X=180 解之,得 X=202X=2×20=40, 3X=3×20=60, 4X=4×20=80答: ∠A 为40度,∠B为60度、 ∠C为80度(1)一个三角形中最多有 个直角?为什吗?
(2)一个三角形中最多有 个钝角?为什吗?
(3)一个三角形中至少有 个锐角?为什吗?
(4)任意 一个三角形中,最大的一个角的度数至少为 .60°211讨论1、如图,某同学把一块三角形的玻璃打碎成三片,现在他要到玻璃店去配一块形状完全一 样的玻璃,那么最省事的办法是 ( )(A)带①去 (B)带②去 (C)带③去 (D)带①和②去C应用创新2、在直角△ABC中,
∠BAC=90度,
AD是高,
找出图中相等的角.
3、在△ABC中,∠A=80°,
∠ ABC和∠A BC的平分线相交于O,
(1)求∠BOC的度数。
(2) 将∠A换个度数,那求出是多少?你能体会∠A和∠BOC有什么关系吗?www.1230.org 初中数学资源网 这节课你有那些收获?
同学们,你们知道其中的道理吗?内角三兄弟之争三角形的三个内角和是多少?把三个角拼在一起试试看?你有什么办法可以验证呢? 从刚才拼角的过程你能想出证明的办法吗?三角形的内角和等于1800.已知△ABC,求证:∠A+∠B+∠C=180°证明1:过A作EF∥BA,
∴∠B=∠2
(两直线平行,内错角相等)
∠C=∠1
(两直线平行,内错角相等)
又∵∠2+∠1+∠BAC=180°
∴∠B+∠C+∠BAC=180°F21ECBA三角形的内角和等于1800.为什么要证明 按照上面的方法,已经可以验证三角形的内角和是180°,但是由于形状不同的三角形有无数多个,我们不可能通过上面的办法一一验证.再加上其验证过程中可能存在误差,不能保证其有效性.所以我们需要一种能证明任意一个三角形的内角和等于180°的方法.这个方法就是—证明.
一个命题是否正确,需要经过使人信服的推理论证才能得出结论.而证明是由命题的题设(已知)出发,经过严密的推理,最后推出结论(求证)正确的过程. 在这里,为了证明的需要,在原来的图形上添画的线叫做辅助线。在平面几何里,辅助线通常画成虚线。返回证明2:延长BC到D,过C作CE∥BA,
∴ ∠A=∠1
(两直线平行,内错角相等)
∠B=∠2
(两直线平行,同位角相等)
又∵∠1+∠2+∠ACB=180°
∴∠A+∠B+∠ACB=180°三角形的内角和等于1800.证明3:过A作AE∥BC,
∴∠B=∠BAE
(两直线平行,内错角相等)
∠EAB+∠BAC+∠C=180°
(两直线平行,同旁内角互补)
∴∠B+∠C+∠BAC=180°三角形的内角和等于1800.思路总结 为了证明三个角的和为1800,转化为一个平角或同旁内角互补,这种转化思想是数学中的常用方法.82 °新知应用 (1)在△ABC中,∠A=55°,∠ B=43 °
则∠A CB= . ∠ ACD=___
(2)在△ABC中,∠A=80°,∠B=∠C , 则∠C=______度。
(3)在直角三角形ABC中,一个锐角为40 °,则另一个锐角是_______度。98°50 50(4) 在△ABC中, ∠A :∠B:∠C=2:3:4,
求∠A 、∠B、 ∠C的度数。
解:设每一份角为X度,则∠A=2X 度、∠B=3X度、 ∠C=4X度,由三角形内角和定理,可得:
2X+3X+4X=180 解之,得 X=202X=2×20=40, 3X=3×20=60, 4X=4×20=80答: ∠A 为40度,∠B为60度、 ∠C为80度(1)一个三角形中最多有 个直角?为什吗?
(2)一个三角形中最多有 个钝角?为什吗?
(3)一个三角形中至少有 个锐角?为什吗?
(4)任意 一个三角形中,最大的一个角的度数至少为 .60°211讨论1、如图,某同学把一块三角形的玻璃打碎成三片,现在他要到玻璃店去配一块形状完全一 样的玻璃,那么最省事的办法是 ( )(A)带①去 (B)带②去 (C)带③去 (D)带①和②去C应用创新2、在直角△ABC中,
∠BAC=90度,
AD是高,
找出图中相等的角.
3、在△ABC中,∠A=80°,
∠ ABC和∠A BC的平分线相交于O,
(1)求∠BOC的度数。
(2) 将∠A换个度数,那求出是多少?你能体会∠A和∠BOC有什么关系吗?www.1230.org 初中数学资源网 这节课你有那些收获?
