7.3.2多边形的内角和与外角和
文档属性
| 名称 | 7.3.2多边形的内角和与外角和 |  | |
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-01-07 14:11:59 | ||
图片预览







文档简介
课件28张PPT。§7.3.2多边形的内角和1、教材的地位和作用
本节课作为第七章第三节,起着承上启下的作用。在内容上,从三角形的内角和到多边形的内角和,再将内角和公式应用于平面镶嵌,环环相扣,层层递进,这样编排易于激发学生的学习兴趣,很适合学生的认知特点。通过这节课的学习,可以培养学生探索与归纳能力,体会到从简单到复杂,从特殊到一般和转化等重要的思想方法。2、教学重点和难点
重点:探索多边形内角和公式。
难点:在探索多边形内角和时,如何把多边形转化成三角形。二、教学目标分析 1、知识与技能:
2、数学思考:
(1)通过测量,类比,推理等教学活动,探索多边形的内角和公式,感受数学思考过程的条理性,发展推理能力和语言表达能力。
(2)通过把多边形转化成三角形体会转化思想在几何中的运用,同时让学生体会从特殊到一般的认识问题的方法。
3、解决问题:通过探索多边形内角和公式,让学生尝试从不同的角度寻求解决问题的方法,并能有效的解决问题。
4、情感态度:通过猜想、推理等数学活动,感受数学活动充满着探索以及数学结论的确定性,体验数学充满探索和创造,从而提高学生的学习热情。三、教法和学法分析 本节课借鉴了美国教育家杜威的“在做中学”的理论和叶圣陶先生所倡导的“解放学生的手,解放学生的大脑,解放学生的时间”的思想,我确定如下教法和学法:
1、教学方法的设计
根据本节课的教学目标、教材内容以及学生的认知特点,我采用启发式、探索式教学方法,意在帮助学生通过观察,自己动手,从实践中获得知识。整个探究学习的过程充满了师生之间、生生之间的交流和互动,体现了教师是教学活动的组织者、引导者、合作者,而学生才是学习的主体。
2、学习方法
利用学生的好奇心设疑、解疑,组织活泼互动、有效的教学活动,鼓励学生积极参与,大胆猜想,使学生在自主探索和合作交流中理解和掌握本节课的内容。
3、现代教育技术的应用
我利用课件辅助教学,适时呈现问题情景,以丰富学生的感性认识,增强直观效果,提高课堂效率。2、学习方法分析 2、学习方法
利用学生的好奇心设疑、解疑,组织活泼互动、有效的教学活动,鼓励学生积极参与,大胆猜想,使学生在自主探索和合作交流中理解和掌握本节课的内容。
3、现代教育技术的应用
我利用课件辅助教学,适时呈现问题情景,以丰富学生的感性认识,增强直观效果,提高课堂效率。1、从n边形的一个顶点可以引_____对角线
将n边形分成了________个三角形。
2、n边形的对角线一共有______条。
(n-3)(n-2)温故知新3、三角形的内角和等于 ____,外角和等____。180○360○
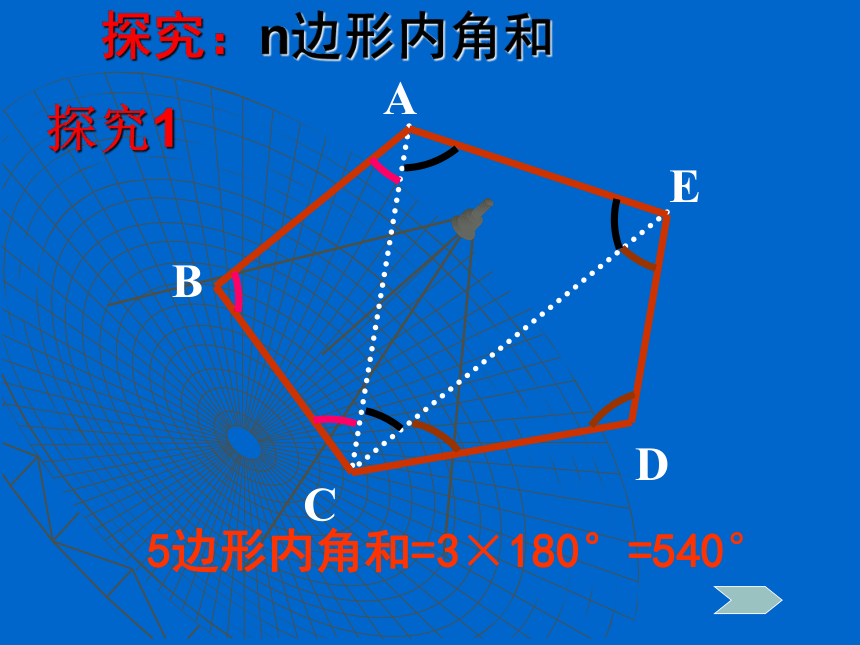
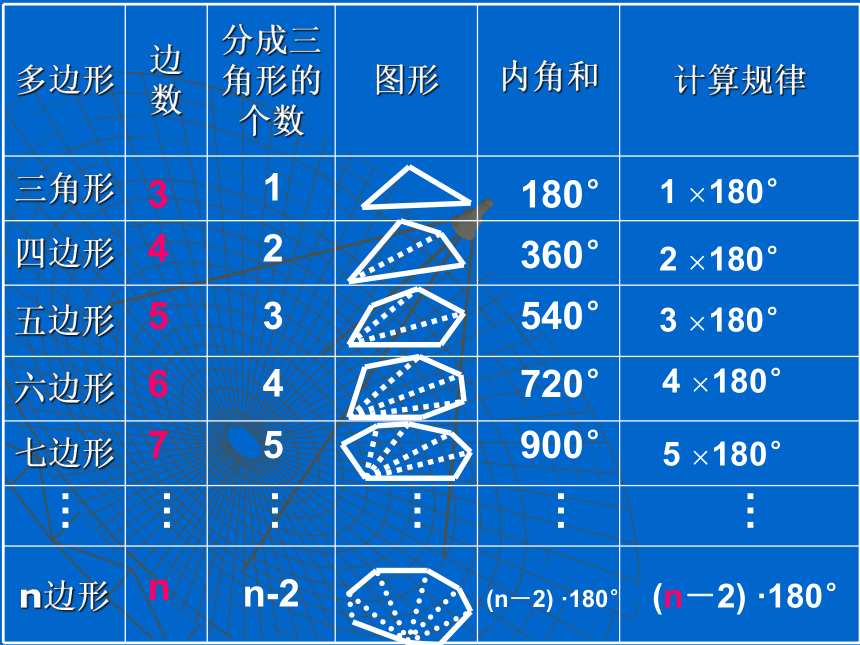
B ACDE探究15边形内角和=3×180°=540°探究:n边形内角和………………34567n1n-22345180°360°540°720°900°(n-2) ·180°(n-2) ·180°5 ×180°4 ×180°3 ×180°2 ×180°1 ×180°总结:n边形内角和公式n边形内角和=(n-2) ·180°反思:我们是怎样求多边形内 角和的?就是从多边形的一个顶点出发,把一个多边形分成几个三角形。O15432O1234如何割法:o把一个五边形分成几个三角形,还有其他的分法吗?n边形内角和公式的应用n边形内角和=(n-2) ·180°练习:看谁求得又快又准!x°140°∟120°150°2x°x°120°80°75°x°X=65X=60X=95火眼金睛(2)(3)例1:已知四边形ABCD,∠A+∠C=180°,求∠B+∠D=?D点评:四边形的一组对角互补,另一组对角也互补。解:四边形的内角和为:(4-2) ×180 =360 °∴ ∠B+∠D= 360 °- (A+∠C)=180° ∠A+∠C=180° 例2 如图,在五边形的每个顶点处各取一个外角,这些外角的和叫做五边形的外角和.五边形的外角和等于多少?
1.任意一个外角和他相邻的内角有什么关系?
2.五个外角加上他们分别相邻的五个内角和是多少?
3.这五个平角和与五边形的内角和、外角和有什么关系? 6 例1 如图,在五边形的每个顶点处各取一个外角,这些外角的和叫做五边形的外角和.五边形的外角和等于多少?
5边形外角和 结论:五边形的外角和等于360°-(5-2) × 180°=360 ° 6=5个平角-5边形内角和=5×180°探究 如果将例2中五边形换成n边(n≥3)
可以得到同样的结果吗?n边形外角和=结论:
n边形的外角和等于360°-(n-2) × 180°=360 °n个平角-n边形内角和=n×180 °从多边形的一个顶点A点出发,沿多边形的各边走过各点之后回到点A.最后再转回出发时的方向。在行程中所转的各个角的和,就是多边形的外角和。由于在这个运动过程中走了一周,也就是说所转的各个角的和等于一个周角。即:多边形的外角和等于360o练一练练习1:如果一个多边形的每一个外等于30°,则这个多边形的边数是_____。12n×30°=360°n=12n边形外角和=360 °练一练练习2:正五边形的每一个外角等于____,每一个内角等于_____。5X=360°X=72°72°144°解:设正五边形的每一个外角度数为x,由
多边形的外角和等于360度可得:所以每一个内角度数为108 °练习. 已知一个多边形,它的内角和等于外角和,它是几边形? 解: 设多边形的边数为n
∵它的内角和等于 (n-2)?180°,
多边形外角和等于360o,
∴ (n-2)?180°= 360o。
解得: n=4
∴这个多边形的边数为4。
感悟与反思n边形内角和=(n-2) ·180°n边形外角和=360°n边形外角和= n个平角-n边形内角和 通过这节课的学习你有哪些收获? 作 业
P84习题7.3 的2、6题 再见 知识拓展
平面镶嵌1、n边形的内角和等于__________,九边形的内角和等于___________。
2、一个多边形当边数增加1时,它的内角和增加( )。
3、已知多边形的每个内角都等于150°,求这个多边形的边数?
4、一个多边形从一个顶点可引对角线3条,这个多边形内角和等于( )
A:360° B:540° C:720° D:900°
5. 已知一个多边形,它的内角和等于外角和的2倍,求这个多边形的边数?
难点:在探索多边形内角和时,如何把多边形转化成三角形。二、教学目标分析 1、知识与技能:
2、数学思考:
(1)通过测量,类比,推理等教学活动,探索多边形的内角和公式,感受数学思考过程的条理性,发展推理能力和语言表达能力。
(2)通过把多边形转化成三角形体会转化思想在几何中的运用,同时让学生体会从特殊到一般的认识问题的方法。
3、解决问题:通过探索多边形内角和公式,让学生尝试从不同的角度寻求解决问题的方法,并能有效的解决问题。
4、情感态度:通过猜想、推理等数学活动,感受数学活动充满着探索以及数学结论的确定性,体验数学充满探索和创造,从而提高学生的学习热情。三、教法和学法分析 本节课借鉴了美国教育家杜威的“在做中学”的理论和叶圣陶先生所倡导的“解放学生的手,解放学生的大脑,解放学生的时间”的思想,我确定如下教法和学法:
1、教学方法的设计
根据本节课的教学目标、教材内容以及学生的认知特点,我采用启发式、探索式教学方法,意在帮助学生通过观察,自己动手,从实践中获得知识。整个探究学习的过程充满了师生之间、生生之间的交流和互动,体现了教师是教学活动的组织者、引导者、合作者,而学生才是学习的主体。
2、学习方法
利用学生的好奇心设疑、解疑,组织活泼互动、有效的教学活动,鼓励学生积极参与,大胆猜想,使学生在自主探索和合作交流中理解和掌握本节课的内容。
3、现代教育技术的应用
我利用课件辅助教学,适时呈现问题情景,以丰富学生的感性认识,增强直观效果,提高课堂效率。2、学习方法分析 2、学习方法
利用学生的好奇心设疑、解疑,组织活泼互动、有效的教学活动,鼓励学生积极参与,大胆猜想,使学生在自主探索和合作交流中理解和掌握本节课的内容。
3、现代教育技术的应用
我利用课件辅助教学,适时呈现问题情景,以丰富学生的感性认识,增强直观效果,提高课堂效率。1、从n边形的一个顶点可以引_____对角线
将n边形分成了________个三角形。
2、n边形的对角线一共有______条。
(n-3)(n-2)温故知新3、三角形的内角和等于 ____,外角和等____。180○360○
B ACDE探究15边形内角和=3×180°=540°探究:n边形内角和………………34567n1n-22345180°360°540°720°900°(n-2) ·180°(n-2) ·180°5 ×180°4 ×180°3 ×180°2 ×180°1 ×180°总结:n边形内角和公式n边形内角和=(n-2) ·180°反思:我们是怎样求多边形内 角和的?就是从多边形的一个顶点出发,把一个多边形分成几个三角形。O15432O1234如何割法:o把一个五边形分成几个三角形,还有其他的分法吗?n边形内角和公式的应用n边形内角和=(n-2) ·180°练习:看谁求得又快又准!x°140°∟120°150°2x°x°120°80°75°x°X=65X=60X=95火眼金睛(2)(3)例1:已知四边形ABCD,∠A+∠C=180°,求∠B+∠D=?D点评:四边形的一组对角互补,另一组对角也互补。解:四边形的内角和为:(4-2) ×180 =360 °∴ ∠B+∠D= 360 °- (A+∠C)=180° ∠A+∠C=180° 例2 如图,在五边形的每个顶点处各取一个外角,这些外角的和叫做五边形的外角和.五边形的外角和等于多少?
1.任意一个外角和他相邻的内角有什么关系?
2.五个外角加上他们分别相邻的五个内角和是多少?
3.这五个平角和与五边形的内角和、外角和有什么关系? 6 例1 如图,在五边形的每个顶点处各取一个外角,这些外角的和叫做五边形的外角和.五边形的外角和等于多少?
5边形外角和 结论:五边形的外角和等于360°-(5-2) × 180°=360 ° 6=5个平角-5边形内角和=5×180°探究 如果将例2中五边形换成n边(n≥3)
可以得到同样的结果吗?n边形外角和=结论:
n边形的外角和等于360°-(n-2) × 180°=360 °n个平角-n边形内角和=n×180 °从多边形的一个顶点A点出发,沿多边形的各边走过各点之后回到点A.最后再转回出发时的方向。在行程中所转的各个角的和,就是多边形的外角和。由于在这个运动过程中走了一周,也就是说所转的各个角的和等于一个周角。即:多边形的外角和等于360o练一练练习1:如果一个多边形的每一个外等于30°,则这个多边形的边数是_____。12n×30°=360°n=12n边形外角和=360 °练一练练习2:正五边形的每一个外角等于____,每一个内角等于_____。5X=360°X=72°72°144°解:设正五边形的每一个外角度数为x,由
多边形的外角和等于360度可得:所以每一个内角度数为108 °练习. 已知一个多边形,它的内角和等于外角和,它是几边形? 解: 设多边形的边数为n
∵它的内角和等于 (n-2)?180°,
多边形外角和等于360o,
∴ (n-2)?180°= 360o。
解得: n=4
∴这个多边形的边数为4。
感悟与反思n边形内角和=(n-2) ·180°n边形外角和=360°n边形外角和= n个平角-n边形内角和 通过这节课的学习你有哪些收获? 作 业
P84习题7.3 的2、6题 再见 知识拓展
平面镶嵌1、n边形的内角和等于__________,九边形的内角和等于___________。
2、一个多边形当边数增加1时,它的内角和增加( )。
3、已知多边形的每个内角都等于150°,求这个多边形的边数?
4、一个多边形从一个顶点可引对角线3条,这个多边形内角和等于( )
A:360° B:540° C:720° D:900°
5. 已知一个多边形,它的内角和等于外角和的2倍,求这个多边形的边数?
