3.3圆周角(2) )
图片预览

文档简介
3.3圆周角(2)
学习目标:
1、理解“直径所对的圆周角是直角”与“90°的圆周角所对的弦是直径”的互逆性,会用这两个定理进行推理论证
2、经历观察、分析,研究图形及与他人合作交流过程,深刻体会度量与证明,分类与转化,以及类比与分类讨论和反证法等教学思想在解决几何问题的作用,提高综合运用数学知识解决问题的能力
教学过程:
自主探究:
预习疑难摘要_______________________
阅读课本 P100“想一想”,回答下列问题⑥
可以通过___、____等方式得出∠A度数
推论中的两个命题互为___命题,它们的题设与结论分别是什么?
如图,OA是圆O的半径,以OA为直径的圆C与圆O的弦AB相交于D点,求证:D是AB的中点
足球场上有句顺口溜“冲向球门跑,越近就越好,歪看球门跑,射点要选好。”如图,在“世界杯”足球比赛中,甲乙两队员互相配合向对方球门PQ进攻,当甲带球冲到A点时,乙已经助攻冲到B点,此时甲自己并没有直接射门,而是迅速将球回传给乙,让乙射门。您能从二人的站位与球门的张角的大小解释甲这样做的合理性吗?
合作交流,成果展示
交流问题2
问题3你找到了几种解法
3、问题4中若甲乙二人的另一名队友丙站在C处,乙最好怎样做⑦
应用规律,巩固新知
初步应用
课本P102 随堂练习1、2
课本P103 习题3
联系拓展
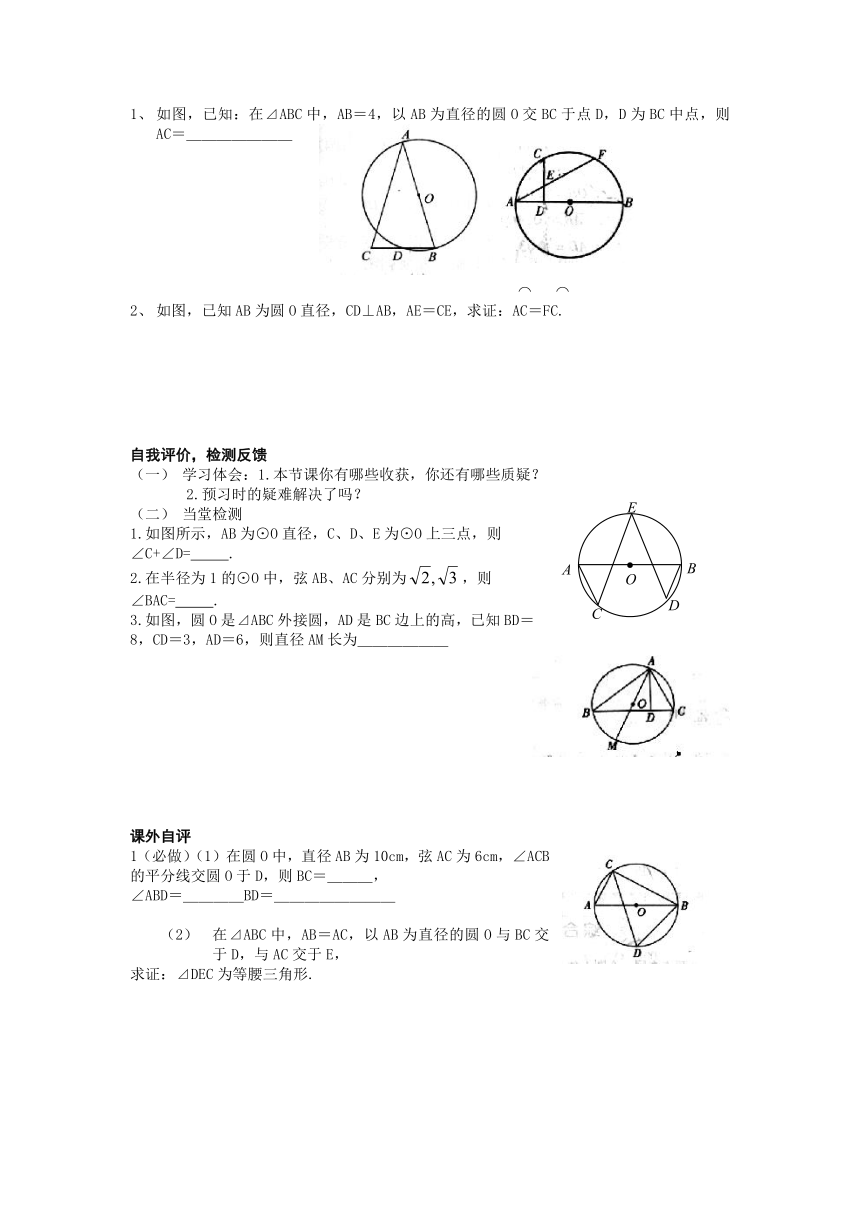
如图,已知:在⊿ABC中,AB=4,以AB为直径的圆O交BC于点D,D为BC中点,则AC=_______
⌒ ⌒
如图,已知AB为圆O直径,CD⊥AB,AE=CE,求证:AC=FC.
自我评价,检测反馈
学习体会:1.本节课你有哪些收获,你还有哪些质疑?
2.预习时的疑难解决了吗?
当堂检测
1.如图所示,AB为⊙O直径,C、D、E为⊙O上三点,则
∠C+∠D= .
2.在半径为1的⊙O中,弦AB、AC分别为,则
∠BAC= .
3.如图,圆O是⊿ABC外接圆,AD是BC边上的高,已知BD=8,CD=3,AD=6,则直径AM长为______
课外自评
1(必做)(1)在圆O中,直径AB为10cm,弦AC为6cm,∠ACB的平分线交圆O于D,则BC=___,
∠ABD=____BD=________
在⊿ABC中,AB=AC,以AB为直径的圆O与BC交于D,与AC交于E,
求证:⊿DEC为等腰三角形.
2、(选做)(1)如图,AB为半圆O的直径,弦AD、BC相交于P点,则CD:AB为( )
sin∠BPC B、cos∠BPC
C、tan∠BPC D、以上都不是
(2)如图,以锐角⊿ABC的一边BC为直径作半圆,交AB于D,交AC于E,
①若DE=BC 求∠A的度数;
②若BC=6cm DE=2cm 求sinA的值.
教(学)后反思
“3.3 圆周角(1)(2)”导学提纲
设计意图与教学建议
数学教学是数学活动的教学,是师生之间交往互动与共同发展的过程,应让学生经历知识的形成与应用过程,从而更好地理解数学知识的意义。
①意在用橡皮筋比较形象地引出圆周角的概念,让学生明白圆周角与圆心角的区别。圆周角有两个特征,缺一不可,对此教师可举出一些反例让学生进行辨析。
②学生在探索这个问题的过程中,将自然地联系到同一弧所对圆周角与它所对的圆心角存在着某种必然联系,同时也加深了对由特殊到一般的思维方式的理解。
③通过射门游戏,发展学生的观察能力,概括归纳出同弧或等弧所对的圆周角大小关系。
④检测学生考虑问题是否全面,教学时应给学生留有时间和空间,让他们进行思考,大胆质疑。
⑤紧密联系实际,让学生从数学角度去观察事物,思考问题,激发对学习的兴趣。
⑥让学生感受到这两个定理的互逆性。
⑦这是学习的难点之一,是一个有实际背景的问题,解决这一问题,既要用到圆周角定理的推论,又要应用分类讨论和反证法思想。教学时可结合课本P102做一做中“危险角”问题拓展归纳出同一弧所对的圆周角、圆内角、圆外角的大小关系。
学习目标:
1、理解“直径所对的圆周角是直角”与“90°的圆周角所对的弦是直径”的互逆性,会用这两个定理进行推理论证
2、经历观察、分析,研究图形及与他人合作交流过程,深刻体会度量与证明,分类与转化,以及类比与分类讨论和反证法等教学思想在解决几何问题的作用,提高综合运用数学知识解决问题的能力
教学过程:
自主探究:
预习疑难摘要_______________________
阅读课本 P100“想一想”,回答下列问题⑥
可以通过___、____等方式得出∠A度数
推论中的两个命题互为___命题,它们的题设与结论分别是什么?
如图,OA是圆O的半径,以OA为直径的圆C与圆O的弦AB相交于D点,求证:D是AB的中点
足球场上有句顺口溜“冲向球门跑,越近就越好,歪看球门跑,射点要选好。”如图,在“世界杯”足球比赛中,甲乙两队员互相配合向对方球门PQ进攻,当甲带球冲到A点时,乙已经助攻冲到B点,此时甲自己并没有直接射门,而是迅速将球回传给乙,让乙射门。您能从二人的站位与球门的张角的大小解释甲这样做的合理性吗?
合作交流,成果展示
交流问题2
问题3你找到了几种解法
3、问题4中若甲乙二人的另一名队友丙站在C处,乙最好怎样做⑦
应用规律,巩固新知
初步应用
课本P102 随堂练习1、2
课本P103 习题3
联系拓展
如图,已知:在⊿ABC中,AB=4,以AB为直径的圆O交BC于点D,D为BC中点,则AC=_______
⌒ ⌒
如图,已知AB为圆O直径,CD⊥AB,AE=CE,求证:AC=FC.
自我评价,检测反馈
学习体会:1.本节课你有哪些收获,你还有哪些质疑?
2.预习时的疑难解决了吗?
当堂检测
1.如图所示,AB为⊙O直径,C、D、E为⊙O上三点,则
∠C+∠D= .
2.在半径为1的⊙O中,弦AB、AC分别为,则
∠BAC= .
3.如图,圆O是⊿ABC外接圆,AD是BC边上的高,已知BD=8,CD=3,AD=6,则直径AM长为______
课外自评
1(必做)(1)在圆O中,直径AB为10cm,弦AC为6cm,∠ACB的平分线交圆O于D,则BC=___,
∠ABD=____BD=________
在⊿ABC中,AB=AC,以AB为直径的圆O与BC交于D,与AC交于E,
求证:⊿DEC为等腰三角形.
2、(选做)(1)如图,AB为半圆O的直径,弦AD、BC相交于P点,则CD:AB为( )
sin∠BPC B、cos∠BPC
C、tan∠BPC D、以上都不是
(2)如图,以锐角⊿ABC的一边BC为直径作半圆,交AB于D,交AC于E,
①若DE=BC 求∠A的度数;
②若BC=6cm DE=2cm 求sinA的值.
教(学)后反思
“3.3 圆周角(1)(2)”导学提纲
设计意图与教学建议
数学教学是数学活动的教学,是师生之间交往互动与共同发展的过程,应让学生经历知识的形成与应用过程,从而更好地理解数学知识的意义。
①意在用橡皮筋比较形象地引出圆周角的概念,让学生明白圆周角与圆心角的区别。圆周角有两个特征,缺一不可,对此教师可举出一些反例让学生进行辨析。
②学生在探索这个问题的过程中,将自然地联系到同一弧所对圆周角与它所对的圆心角存在着某种必然联系,同时也加深了对由特殊到一般的思维方式的理解。
③通过射门游戏,发展学生的观察能力,概括归纳出同弧或等弧所对的圆周角大小关系。
④检测学生考虑问题是否全面,教学时应给学生留有时间和空间,让他们进行思考,大胆质疑。
⑤紧密联系实际,让学生从数学角度去观察事物,思考问题,激发对学习的兴趣。
⑥让学生感受到这两个定理的互逆性。
⑦这是学习的难点之一,是一个有实际背景的问题,解决这一问题,既要用到圆周角定理的推论,又要应用分类讨论和反证法思想。教学时可结合课本P102做一做中“危险角”问题拓展归纳出同一弧所对的圆周角、圆内角、圆外角的大小关系。
