北师大版 八年级数学下册 1.1 等腰三角形 课件(共17张PPT)
文档属性
| 名称 | 北师大版 八年级数学下册 1.1 等腰三角形 课件(共17张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 763.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-21 20:24:53 | ||
图片预览




文档简介
(共17张PPT)
第一章 三角形的证明
三角形全等判定定理:
1.三边对应相等的两个三角形全等(SSS)。
2.两边及其夹角对应相等的两个三角形
全等(SAS)。
3.两角及其夹边对应相等的两个三角形
全等(ASA)。
4.两角及其中一角的对应边相等的两个 三角形全等(AAS)
全等三角形的对应边、对应角相等。
你还记得我们探索过的等腰三角形的性质吗
推论:
等腰三角形顶角的平分线,底边上的中线 底边上的高互相重合(三线合一).
你能利用已有的公理和定理证明这些结论吗
定理:
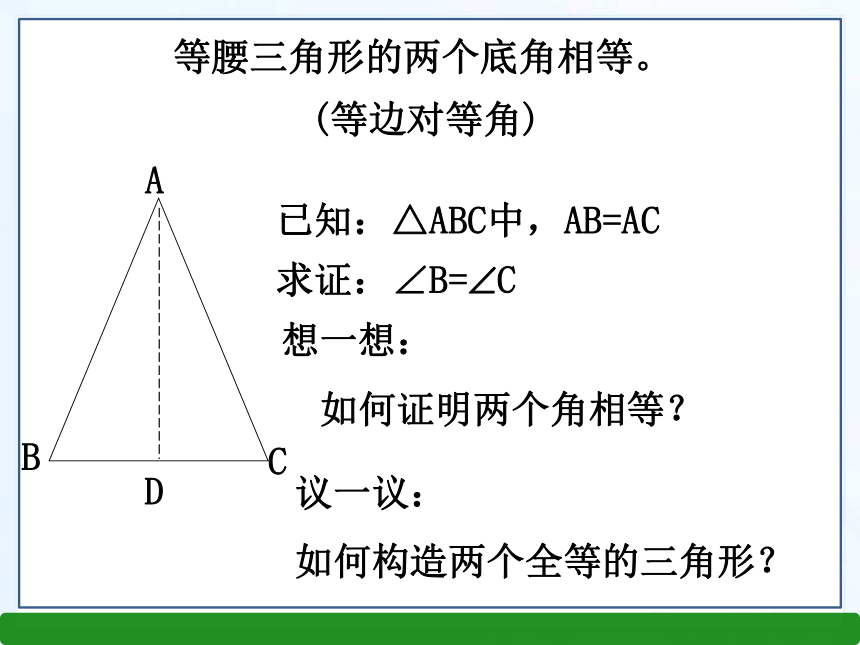
等腰三角形的两个底角相等.
(等边对等角)
等腰三角形的两个底角相等。
A
B
C
D
已知:△ABC中,AB=AC
求证:∠B= C
想一想:
如何证明两个角相等?
议一议:
如何构造两个全等的三角形?
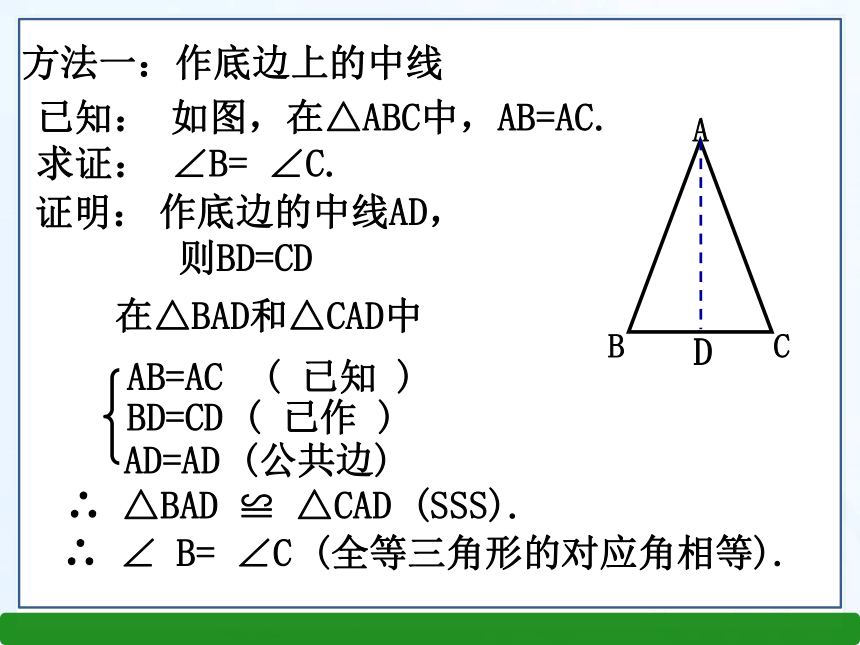
已知: 如图,在△ABC中,AB=AC.
求证: ∠B= ∠C.
A
B
C
D
证明:
作底边的中线AD,
则BD=CD
AB=AC ( 已知 )
BD=CD ( 已作 )
AD=AD (公共边)
∴ △BAD ≌ △CAD (SSS).
∴ ∠ B= ∠C (全等三角形的对应角相等).
在△BAD和△CAD中
方法一:作底边上的中线
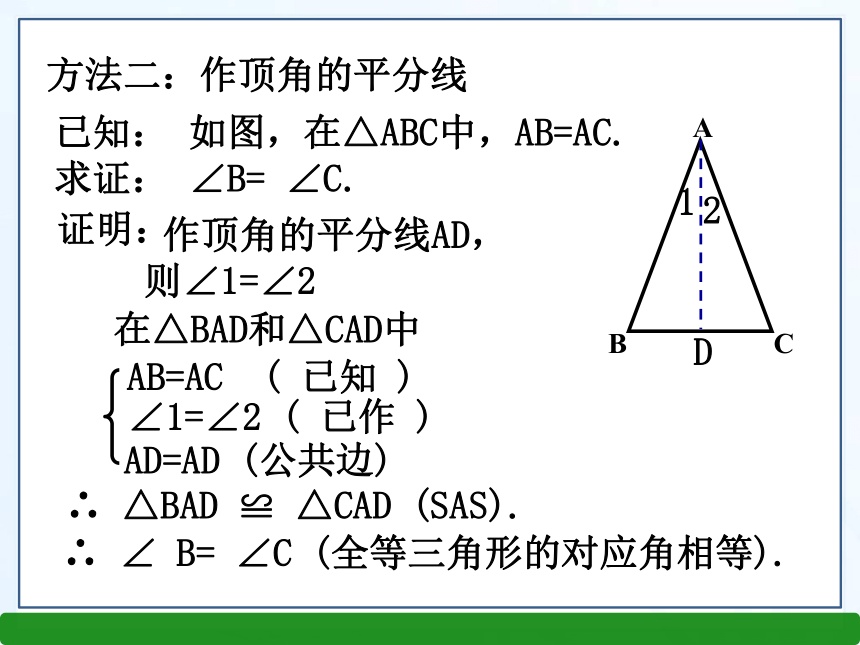
已知: 如图,在△ABC中,AB=AC.
求证: ∠B= ∠C.
A
B
C
D
证明:
作顶角的平分线AD,
则∠1=∠2
AB=AC ( 已知 )
∠1=∠2 ( 已作 )
AD=AD (公共边)
∴ △BAD ≌ △CAD (SAS).
∴ ∠ B= ∠C (全等三角形的对应角相等).
方法二:作顶角的平分线
在△BAD和△CAD中
1
2
已知: 如图,在△ABC中,AB=AC.
求证: ∠B= ∠C.
A
B
C
D
证明:
作底边的高线AD,则∠BDA=∠CDA=90°
AB=AC ( 已知 )
AD=AD (公共边)
∴ Rt△BAD ≌ Rt△CAD (HL).
∴ ∠ B= ∠C (全等三角形的对应角相等).
方法三:作底边的高线
在Rt△BAD和Rt△CAD中
定理:
等腰三角形的两个底角相等(等边对等角).
A
C
B
如图,在△ABC中,
∵AB=AC(已知),
∴∠B=∠C(等边对等角).
证明后的结论,以后可以直接运用.
思考:
由△BAD ≌ △CAD,除了可以得到
∠ B= ∠C之外,你还可以得到那些
相等的线段和相等的角?和你的同伴
交流一下,看看你有什么新的发现?
根据等腰三角形的性质,
在△ABC中, AB=AC时,
(1) ∵AD⊥BC,∴∠_____ = ∠_____,____= ____.
(2) ∵AD是中线,∴____⊥____ ,∠_____ =∠_____.
(3) ∵AD是角平分线,∴____ ⊥____ ,_____ =_____.
A
B
C
D
BAD
CAD
CAD
BD
CD
AD
BC
BD
BAD
BC
AD
CD
(1)如果等腰三角形的一个底角为50°,
则其余两个角为____和____.
(2)如果等腰三角形的顶角为80°,则它的 一个底角为____.
50°
80°
50°
(3)如果等腰三角形的一个角为80°,则其余两个角为________________________.
80°和20°
(4)如果等腰三角形的一个角为100°,则其余两个角为_________.
40°和40°
或50°和50 °
1.已知等腰三角形的两条边长分别是7和3,则下列四个数中,第三条边的长是( )
A. 8 B. 7 C. 4 D. 3.
2.如图,在△ABC中,AB=AC,∠A=36°,BD、CE分别是△ABC、△BCD的角平分线,则图中的等腰三角形有( )
A.5个 B.4个
C.3个 D.2个
A
B
3.如图,在三角形ABD中,C是BD上的一点,
且AC垂直BD,AC=BC=CD.
(1) 求证:△ABD是等腰三角形
(2)求∠ABD的度数
A
B
C
D
4.将下面证明中每一步的理由写在括号内:
已知:如图,AB=CD,AD=CB.
求证:∠A=∠C.
证明:连接BD,
在△BAD和△DCB中,
∵ AB=CD( )
AD=CB( )
BD=DB( )
∴ △BAD≌ △DCB( )
∴ :∠A=∠C ( )
A
B
C
D
5.已知:如图,点B,E,
C,F在同一条直线上,AB=DE,AC=DF,BE=CF.
求证:∠A=∠D
A
B
C
D
E
F
等腰三角形的性质:
性质1 等腰三角形的两个底角相等(简写成“等边对等角”).
性质2 等腰三角形的顶角平分线、底边上的
中线、底边上的高互相重合( “三线合一”).即:等腰三角形顶角的角平分线垂直平分底边.
第一章 三角形的证明
三角形全等判定定理:
1.三边对应相等的两个三角形全等(SSS)。
2.两边及其夹角对应相等的两个三角形
全等(SAS)。
3.两角及其夹边对应相等的两个三角形
全等(ASA)。
4.两角及其中一角的对应边相等的两个 三角形全等(AAS)
全等三角形的对应边、对应角相等。
你还记得我们探索过的等腰三角形的性质吗
推论:
等腰三角形顶角的平分线,底边上的中线 底边上的高互相重合(三线合一).
你能利用已有的公理和定理证明这些结论吗
定理:
等腰三角形的两个底角相等.
(等边对等角)
等腰三角形的两个底角相等。
A
B
C
D
已知:△ABC中,AB=AC
求证:∠B= C
想一想:
如何证明两个角相等?
议一议:
如何构造两个全等的三角形?
已知: 如图,在△ABC中,AB=AC.
求证: ∠B= ∠C.
A
B
C
D
证明:
作底边的中线AD,
则BD=CD
AB=AC ( 已知 )
BD=CD ( 已作 )
AD=AD (公共边)
∴ △BAD ≌ △CAD (SSS).
∴ ∠ B= ∠C (全等三角形的对应角相等).
在△BAD和△CAD中
方法一:作底边上的中线
已知: 如图,在△ABC中,AB=AC.
求证: ∠B= ∠C.
A
B
C
D
证明:
作顶角的平分线AD,
则∠1=∠2
AB=AC ( 已知 )
∠1=∠2 ( 已作 )
AD=AD (公共边)
∴ △BAD ≌ △CAD (SAS).
∴ ∠ B= ∠C (全等三角形的对应角相等).
方法二:作顶角的平分线
在△BAD和△CAD中
1
2
已知: 如图,在△ABC中,AB=AC.
求证: ∠B= ∠C.
A
B
C
D
证明:
作底边的高线AD,则∠BDA=∠CDA=90°
AB=AC ( 已知 )
AD=AD (公共边)
∴ Rt△BAD ≌ Rt△CAD (HL).
∴ ∠ B= ∠C (全等三角形的对应角相等).
方法三:作底边的高线
在Rt△BAD和Rt△CAD中
定理:
等腰三角形的两个底角相等(等边对等角).
A
C
B
如图,在△ABC中,
∵AB=AC(已知),
∴∠B=∠C(等边对等角).
证明后的结论,以后可以直接运用.
思考:
由△BAD ≌ △CAD,除了可以得到
∠ B= ∠C之外,你还可以得到那些
相等的线段和相等的角?和你的同伴
交流一下,看看你有什么新的发现?
根据等腰三角形的性质,
在△ABC中, AB=AC时,
(1) ∵AD⊥BC,∴∠_____ = ∠_____,____= ____.
(2) ∵AD是中线,∴____⊥____ ,∠_____ =∠_____.
(3) ∵AD是角平分线,∴____ ⊥____ ,_____ =_____.
A
B
C
D
BAD
CAD
CAD
BD
CD
AD
BC
BD
BAD
BC
AD
CD
(1)如果等腰三角形的一个底角为50°,
则其余两个角为____和____.
(2)如果等腰三角形的顶角为80°,则它的 一个底角为____.
50°
80°
50°
(3)如果等腰三角形的一个角为80°,则其余两个角为________________________.
80°和20°
(4)如果等腰三角形的一个角为100°,则其余两个角为_________.
40°和40°
或50°和50 °
1.已知等腰三角形的两条边长分别是7和3,则下列四个数中,第三条边的长是( )
A. 8 B. 7 C. 4 D. 3.
2.如图,在△ABC中,AB=AC,∠A=36°,BD、CE分别是△ABC、△BCD的角平分线,则图中的等腰三角形有( )
A.5个 B.4个
C.3个 D.2个
A
B
3.如图,在三角形ABD中,C是BD上的一点,
且AC垂直BD,AC=BC=CD.
(1) 求证:△ABD是等腰三角形
(2)求∠ABD的度数
A
B
C
D
4.将下面证明中每一步的理由写在括号内:
已知:如图,AB=CD,AD=CB.
求证:∠A=∠C.
证明:连接BD,
在△BAD和△DCB中,
∵ AB=CD( )
AD=CB( )
BD=DB( )
∴ △BAD≌ △DCB( )
∴ :∠A=∠C ( )
A
B
C
D
5.已知:如图,点B,E,
C,F在同一条直线上,AB=DE,AC=DF,BE=CF.
求证:∠A=∠D
A
B
C
D
E
F
等腰三角形的性质:
性质1 等腰三角形的两个底角相等(简写成“等边对等角”).
性质2 等腰三角形的顶角平分线、底边上的
中线、底边上的高互相重合( “三线合一”).即:等腰三角形顶角的角平分线垂直平分底边.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
