2021-2022学年人教版数学八年级下册第十八章平行四边形单元巩固训练卷(一)(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版数学八年级下册第十八章平行四边形单元巩固训练卷(一)(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 454.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-21 15:26:04 | ||
图片预览



文档简介
2020—2021学年八年级下学期数学期末第十八章
平行四边形 单元巩固训练卷(一)
一、单选题
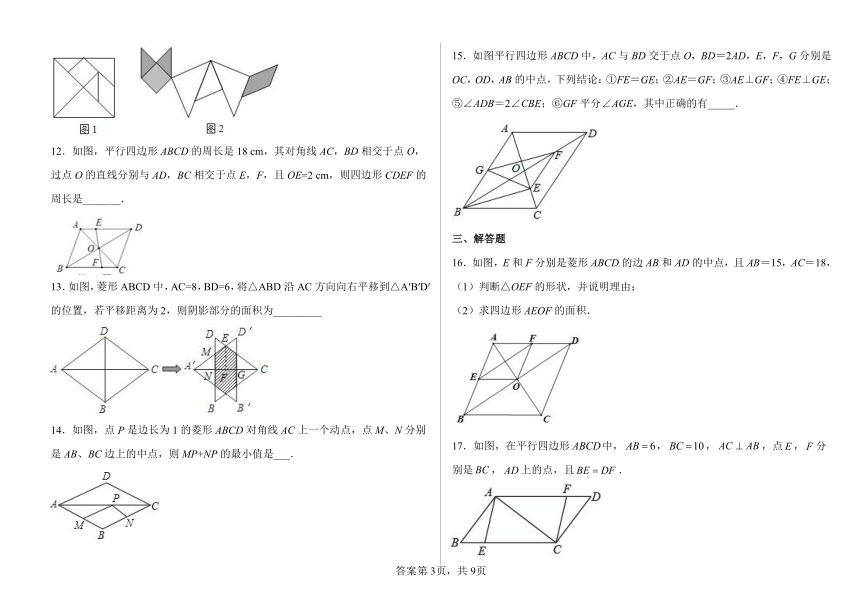
1.如图, ABCD中,点O为对角线AC、BD的交点,点E为CD边的中点,连接OE,如果AB=4,OE=3,则 ABCD的周长为( )
A.7 B.10 C.14 D.20
2.如图,有一块形状为的铁板余料,已知要把它加工成一个形状为的工件,使在上,两点分别在上,且,则的面积为( )
A. B.
C. D.
3.如图,在中,,点E在BD上,.如果,那么等于( )
A.20° B.25° C.30° D.35°
4.王老师把两张长为,宽为的矩形纸条按如图所示的形状交叉叠放在一起,根据所学的知识,我们可以判定重合部分构成的四边形是菱形.则随着纸条的转动,菱形的面积的最大值与最小值的和为( )
A. B. C. D.
5.如图,中,对角线,相交于点,下列条件:(1);(2);(3),其中能判定是菱形的条件有( )
A.0个 B.1个 C.2个 D.3个
6.如图,在平行四边形ABCD中,AD=2AB,F是BC的中点,作AE⊥CD于点E,连接EF、AF,下列结论:①2∠BAF=∠BAD;②EF=AF;③S△ABF=S△AEF;④∠BFE=3∠CEF.其中一定成立的个数是( )
A.1个 B.2个 C.3个 D.4个
7.如图,正方形和正方形的顶点在同一直线上,且,给出下列结论:①,②,③④,其中正确的个数为( )
A.个 B.个 C.个 D.个
8.将四根长度相等的细木条首尾相接,用钉子钉成四边形,转动这个四边形,使它形状改变,当时,如图1,测得,当时,如图2,则的值为( )
A. B.2 C. D.
9.如图,平行四边形 ABCD 中, E为 BC 边上一点,以 AE 为边作正方形AEFG,若 ,,则 的度数是
A. B. C. D.
10.如图,四边形ABCD是平行四边形,下列说法不正确的是( )
A.当AC=BD时,四边形ABCD是矩形
B.当AC⊥BD时,四边形ABCD是菱形
C.当AC平分∠BAD时,四边形ABCD是菱形
D.当∠DAB=90°时,四边形ABCD是正方形
二、填空题
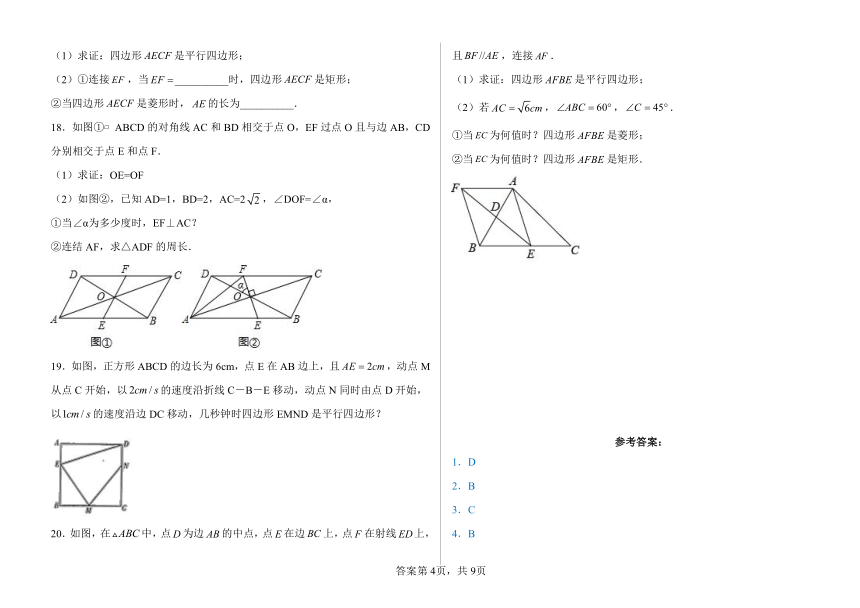
11.七巧板被西方人称为“东方魔术”.下面的两幅图是由同一副七巧板拼成的.已知七巧板拼成的正方形(如图1)边长为.若图2的“小狐狸”图案中的阴影部分面积为,那么________.
12.如图,平行四边形ABCD的周长是18 cm,其对角线AC,BD相交于点O,过点O的直线分别与AD,BC相交于点E,F,且OE=2 cm,则四边形CDEF的周长是_______.
13.如图,菱形ABCD中,AC=8,BD=6,将△ABD沿AC方向向右平移到△A′B′D′的位置,若平移距离为2,则阴影部分的面积为_________
14.如图,点P是边长为1的菱形ABCD对角线AC上一个动点,点M、N分别是AB、BC边上的中点,则MP+NP的最小值是___.
15.如图平行四边形ABCD中,AC与BD交于点O,BD=2AD,E,F,G分别是OC,OD,AB的中点,下列结论:①FE=GE;②AE=GF;③AE⊥GF;④FE⊥GE;⑤∠ADB=2∠CBE;⑥GF平分∠AGE,其中正确的有_____.
三、解答题
16.如图,E和F分别是菱形ABCD的边AB和AD的中点,且AB=15,AC=18,
(1)判断△OEF的形状,并说明理由;
(2)求四边形AEOF的面积.
17.如图,在平行四边形中,,,,点,分别是,上的点,且.
(1)求证:四边形是平行四边形;
(2)①连接,当__________时,四边形是矩形;
②当四边形是菱形时,的长为__________.
18.如图① ABCD的对角线AC和BD相交于点O,EF过点O且与边AB,CD分别相交于点E和点F.
(1)求证:OE=OF
(2)如图②,已知AD=1,BD=2,AC=2,∠DOF=∠α,
①当∠α为多少度时,EF⊥AC?
②连结AF,求△ADF的周长.
19.如图,正方形ABCD的边长为6cm,点E在AB边上,且,动点M从点C开始,以的速度沿折线C-B-E移动,动点N同时由点D开始,以的速度沿边DC移动,几秒钟时四边形EMND是平行四边形?
20.如图,在中,点为边的中点,点在边上,点在射线上,且,连接.
(1)求证:四边形是平行四边形;
(2)若,,.
①当为何值时?四边形是菱形;
②当为何值时?四边形是矩形.
参考答案:
1.D
2.B
3.C
4.B
5.C
6.C
7.B
8.A
9.A
10.D
11.4
12.13cm
13.7.5.
14.1
解:作点M关于AC的对称点,连接P,
∵菱形ABCD关于AC对称,点M关于AC的对称点,点M是AB的中点,
∴点是AD的中点,MP=P,
∴MP+NP=P +NP,
∴当点、P、N三点共线时,MP+NP有最小值为线段N的长.
当点、P、N三点共线时,
∵点是AD的中点,点N是BC边上的中点,
∴,,
∵在菱形ABCD中,
∴ADBC,AD=BC,
∴ABN,A=BN,
∴四边形ANB是平行四边形,
∴N=AB=1,
∴MP+NP的最小值是1.
15.①③⑤⑥
解:①∵四边形ABCD是平行四边形,
∴AD//BC,AD=BC,DO=BO=BD,
∵BD=2AD,
∴AD=DO,BC=BO,
∴△BOC是等腰三角形,
∵E是CO中点,
∴EB⊥CO,
∴∠BEA=90°,
∵G为AB中点,
∴EG=AB,
∵四边形ABCD是平行四边形,
∴AB=CD,
∵E、F分别是OC、OD的中点,
∴EF=CD,
∴EG=EF,
故①正确;
②连接AF,
Rt△AEB中,G是AB的中点,
∴EG=AB=AG,
∵EG=EF,
∴AG=EF,
∵E、F分别是OC、OD的中点,
∴EF//CD,
∵AB//CD,
∴AG//EF,
∴四边形AGEF是菱形,
∴AE⊥FG,GF平分∠AGE,
故②错误,③⑥正确;
③∵E、F分别是OC、OD的中点,
∴EF//DC,
∵DC//AB,
∴EF//AB,
∴∠EFG=∠AGF,
∵EF=EG,
∴∠EFG=∠EGF,
∴∠EGF=∠AGF,
∴GF平分∠AGE,故③正确;
④由①知:BE⊥AE,
由②、③得:EF//AB,EF=CD=AB=BG,
∴四边形BEFG是平行四边形,
∵EG=EF,
∴要使EF⊥GE,则∠EFG=∠EBA=∠EAB=45°,
没有条件AE=BE,或∠BAC=45°,故④错误;
⑤∵AD//BC,
∴∠ADB=∠CBD=2∠CBE,
∴故⑤正确;
本题正确的有:①③⑤⑥.
16.(1)等腰三角形,理由如下;(2)54
解:(1)△OEF是等腰三角形,理由如下:
∵四边形ABCD是菱形,
∴AB=AD,OB=OD,
∵E、F分别是AB、AD的中点,OB=OD,
∴OE、OF是△ABD的中位线,
∴OE=AD,OF=AB,OEAD, OFAB,
又∵AB=AD,
∴OE=OF,
∴△OEF是等腰三角形.
(2)∵四边形ABCD是菱形,
∴OA=OC=AC=9,AC⊥BD,
∴∠AOB=90°,
∴OB===12,
∴BD=2OB=24,
∵E、F分别是AB、AD的中点,
∴EF是△ABD的中位线,
∴EF=BD=12,EFBD.
∵AC⊥BD,
∴AC⊥EF.
∵OEAD, OFAB,
∴四边形AEOF为平行四边形,
又∵AC⊥EF.
∴四边形AEOF为菱形,
∴
=
=54.
17.(1)如下;(2)①8;②5.
解:(1)证明:∵四边形是平行四边形,
∴,.
∵,
∴,
∴四边形是平行四边形.
(2)①连接,如图
∵四边形是矩形,
∴;
∵,
∴,
∵,,
∴,
∴,
故答案为:8.
②连接,如图
∵四边形是菱形,
∴,点G是AC的中点,
∴AB∥EF,,
∴,
∵,
∴;
18.(1)证明如下;(2)①当为时,;②的周长为.
(1)∵四边形ABCD 是平行四边形
∴
∴
在和中,
∴
∴;
(2)①∵四边形ABCD 是平行四边形,
∴
又
∴
是等腰直角三角形
若,则
∴
故当为时,;
②∵四边形ABCD 是平行四边形
又∵
∴EF垂直平分AC
∴
由①知,,即
则的周长为
故的周长为.
19.秒
20.(1)如下;(2)①;②.
(1)证明:∵,
∴∠DBF=∠DAE,∠BFD=∠AED,
∵点为边的中点,
∴BD=AD,
∴,
∴,
∴四边形是平行四边形;
(2)①过点A作AM⊥BE,
∵,,
∴是等腰直角三角形,
∴AM=CM=,
当四边形是菱形时,BE=AE,
∵,
∴是等边三角形,
∴BM=EM=AM÷= ÷=1cm,
∴CE=CM-ME=;
②∵,,当四边形是矩形时,则AE⊥BC,
∴是等腰直角三角形,
∴AM=CM=,
∴AE=EC=.答案第1页,共2页
答案第9页,共9页
平行四边形 单元巩固训练卷(一)
一、单选题
1.如图, ABCD中,点O为对角线AC、BD的交点,点E为CD边的中点,连接OE,如果AB=4,OE=3,则 ABCD的周长为( )
A.7 B.10 C.14 D.20
2.如图,有一块形状为的铁板余料,已知要把它加工成一个形状为的工件,使在上,两点分别在上,且,则的面积为( )
A. B.
C. D.
3.如图,在中,,点E在BD上,.如果,那么等于( )
A.20° B.25° C.30° D.35°
4.王老师把两张长为,宽为的矩形纸条按如图所示的形状交叉叠放在一起,根据所学的知识,我们可以判定重合部分构成的四边形是菱形.则随着纸条的转动,菱形的面积的最大值与最小值的和为( )
A. B. C. D.
5.如图,中,对角线,相交于点,下列条件:(1);(2);(3),其中能判定是菱形的条件有( )
A.0个 B.1个 C.2个 D.3个
6.如图,在平行四边形ABCD中,AD=2AB,F是BC的中点,作AE⊥CD于点E,连接EF、AF,下列结论:①2∠BAF=∠BAD;②EF=AF;③S△ABF=S△AEF;④∠BFE=3∠CEF.其中一定成立的个数是( )
A.1个 B.2个 C.3个 D.4个
7.如图,正方形和正方形的顶点在同一直线上,且,给出下列结论:①,②,③④,其中正确的个数为( )
A.个 B.个 C.个 D.个
8.将四根长度相等的细木条首尾相接,用钉子钉成四边形,转动这个四边形,使它形状改变,当时,如图1,测得,当时,如图2,则的值为( )
A. B.2 C. D.
9.如图,平行四边形 ABCD 中, E为 BC 边上一点,以 AE 为边作正方形AEFG,若 ,,则 的度数是
A. B. C. D.
10.如图,四边形ABCD是平行四边形,下列说法不正确的是( )
A.当AC=BD时,四边形ABCD是矩形
B.当AC⊥BD时,四边形ABCD是菱形
C.当AC平分∠BAD时,四边形ABCD是菱形
D.当∠DAB=90°时,四边形ABCD是正方形
二、填空题
11.七巧板被西方人称为“东方魔术”.下面的两幅图是由同一副七巧板拼成的.已知七巧板拼成的正方形(如图1)边长为.若图2的“小狐狸”图案中的阴影部分面积为,那么________.
12.如图,平行四边形ABCD的周长是18 cm,其对角线AC,BD相交于点O,过点O的直线分别与AD,BC相交于点E,F,且OE=2 cm,则四边形CDEF的周长是_______.
13.如图,菱形ABCD中,AC=8,BD=6,将△ABD沿AC方向向右平移到△A′B′D′的位置,若平移距离为2,则阴影部分的面积为_________
14.如图,点P是边长为1的菱形ABCD对角线AC上一个动点,点M、N分别是AB、BC边上的中点,则MP+NP的最小值是___.
15.如图平行四边形ABCD中,AC与BD交于点O,BD=2AD,E,F,G分别是OC,OD,AB的中点,下列结论:①FE=GE;②AE=GF;③AE⊥GF;④FE⊥GE;⑤∠ADB=2∠CBE;⑥GF平分∠AGE,其中正确的有_____.
三、解答题
16.如图,E和F分别是菱形ABCD的边AB和AD的中点,且AB=15,AC=18,
(1)判断△OEF的形状,并说明理由;
(2)求四边形AEOF的面积.
17.如图,在平行四边形中,,,,点,分别是,上的点,且.
(1)求证:四边形是平行四边形;
(2)①连接,当__________时,四边形是矩形;
②当四边形是菱形时,的长为__________.
18.如图① ABCD的对角线AC和BD相交于点O,EF过点O且与边AB,CD分别相交于点E和点F.
(1)求证:OE=OF
(2)如图②,已知AD=1,BD=2,AC=2,∠DOF=∠α,
①当∠α为多少度时,EF⊥AC?
②连结AF,求△ADF的周长.
19.如图,正方形ABCD的边长为6cm,点E在AB边上,且,动点M从点C开始,以的速度沿折线C-B-E移动,动点N同时由点D开始,以的速度沿边DC移动,几秒钟时四边形EMND是平行四边形?
20.如图,在中,点为边的中点,点在边上,点在射线上,且,连接.
(1)求证:四边形是平行四边形;
(2)若,,.
①当为何值时?四边形是菱形;
②当为何值时?四边形是矩形.
参考答案:
1.D
2.B
3.C
4.B
5.C
6.C
7.B
8.A
9.A
10.D
11.4
12.13cm
13.7.5.
14.1
解:作点M关于AC的对称点,连接P,
∵菱形ABCD关于AC对称,点M关于AC的对称点,点M是AB的中点,
∴点是AD的中点,MP=P,
∴MP+NP=P +NP,
∴当点、P、N三点共线时,MP+NP有最小值为线段N的长.
当点、P、N三点共线时,
∵点是AD的中点,点N是BC边上的中点,
∴,,
∵在菱形ABCD中,
∴ADBC,AD=BC,
∴ABN,A=BN,
∴四边形ANB是平行四边形,
∴N=AB=1,
∴MP+NP的最小值是1.
15.①③⑤⑥
解:①∵四边形ABCD是平行四边形,
∴AD//BC,AD=BC,DO=BO=BD,
∵BD=2AD,
∴AD=DO,BC=BO,
∴△BOC是等腰三角形,
∵E是CO中点,
∴EB⊥CO,
∴∠BEA=90°,
∵G为AB中点,
∴EG=AB,
∵四边形ABCD是平行四边形,
∴AB=CD,
∵E、F分别是OC、OD的中点,
∴EF=CD,
∴EG=EF,
故①正确;
②连接AF,
Rt△AEB中,G是AB的中点,
∴EG=AB=AG,
∵EG=EF,
∴AG=EF,
∵E、F分别是OC、OD的中点,
∴EF//CD,
∵AB//CD,
∴AG//EF,
∴四边形AGEF是菱形,
∴AE⊥FG,GF平分∠AGE,
故②错误,③⑥正确;
③∵E、F分别是OC、OD的中点,
∴EF//DC,
∵DC//AB,
∴EF//AB,
∴∠EFG=∠AGF,
∵EF=EG,
∴∠EFG=∠EGF,
∴∠EGF=∠AGF,
∴GF平分∠AGE,故③正确;
④由①知:BE⊥AE,
由②、③得:EF//AB,EF=CD=AB=BG,
∴四边形BEFG是平行四边形,
∵EG=EF,
∴要使EF⊥GE,则∠EFG=∠EBA=∠EAB=45°,
没有条件AE=BE,或∠BAC=45°,故④错误;
⑤∵AD//BC,
∴∠ADB=∠CBD=2∠CBE,
∴故⑤正确;
本题正确的有:①③⑤⑥.
16.(1)等腰三角形,理由如下;(2)54
解:(1)△OEF是等腰三角形,理由如下:
∵四边形ABCD是菱形,
∴AB=AD,OB=OD,
∵E、F分别是AB、AD的中点,OB=OD,
∴OE、OF是△ABD的中位线,
∴OE=AD,OF=AB,OEAD, OFAB,
又∵AB=AD,
∴OE=OF,
∴△OEF是等腰三角形.
(2)∵四边形ABCD是菱形,
∴OA=OC=AC=9,AC⊥BD,
∴∠AOB=90°,
∴OB===12,
∴BD=2OB=24,
∵E、F分别是AB、AD的中点,
∴EF是△ABD的中位线,
∴EF=BD=12,EFBD.
∵AC⊥BD,
∴AC⊥EF.
∵OEAD, OFAB,
∴四边形AEOF为平行四边形,
又∵AC⊥EF.
∴四边形AEOF为菱形,
∴
=
=54.
17.(1)如下;(2)①8;②5.
解:(1)证明:∵四边形是平行四边形,
∴,.
∵,
∴,
∴四边形是平行四边形.
(2)①连接,如图
∵四边形是矩形,
∴;
∵,
∴,
∵,,
∴,
∴,
故答案为:8.
②连接,如图
∵四边形是菱形,
∴,点G是AC的中点,
∴AB∥EF,,
∴,
∵,
∴;
18.(1)证明如下;(2)①当为时,;②的周长为.
(1)∵四边形ABCD 是平行四边形
∴
∴
在和中,
∴
∴;
(2)①∵四边形ABCD 是平行四边形,
∴
又
∴
是等腰直角三角形
若,则
∴
故当为时,;
②∵四边形ABCD 是平行四边形
又∵
∴EF垂直平分AC
∴
由①知,,即
则的周长为
故的周长为.
19.秒
20.(1)如下;(2)①;②.
(1)证明:∵,
∴∠DBF=∠DAE,∠BFD=∠AED,
∵点为边的中点,
∴BD=AD,
∴,
∴,
∴四边形是平行四边形;
(2)①过点A作AM⊥BE,
∵,,
∴是等腰直角三角形,
∴AM=CM=,
当四边形是菱形时,BE=AE,
∵,
∴是等边三角形,
∴BM=EM=AM÷= ÷=1cm,
∴CE=CM-ME=;
②∵,,当四边形是矩形时,则AE⊥BC,
∴是等腰直角三角形,
∴AM=CM=,
∴AE=EC=.答案第1页,共2页
答案第9页,共9页
