2021-2022学年北师大数学八年级下册第一章三角形的证明章节总复习B(Word版含答案)
文档属性
| 名称 | 2021-2022学年北师大数学八年级下册第一章三角形的证明章节总复习B(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 691.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-21 15:28:30 | ||
图片预览



文档简介
北师大数学八年级下册第一章 三角形的证明 章节总复习B(含答案)
姓名:___________班级:___________
一、单选题
1.如图,已知∠ABC,小彬借助一把没有刻度且等宽的直尺,按如图的方法画出了∠ABC的平分线BP.他这样做的依据是( )
A.在一个角的内部,且到角两边的距离相等的点在这个角的平分线上
B.角平分线上的点到这个角两边的距离相等
C.三角形三条角平分线的交点到三条边的距离相等
D.测量垂直平分线上的点到这条线段的距离相等
2.如图,在△PAB中,PA=PB,M,N,K分别是PA,PB,AB上的点,且AM=BK,BN=AK,若∠MKN=42°,则∠P的度数为( )
A.44° B.66° C.96° D.92°
3.下列能断定△ABC为等腰三角形的是( )
A.∠A=40°,∠B=50° B.∠A=2∠B=70°
C.∠A=40°,∠B=70° D.AB=3,BC=6,周长为14
4.如图,在中,,为中点.若,,则的度数为( )
A. B. C. D.
5.如图,已知的面积为,为的平分线,于点,则的面积为( ).
A. B. C. D.
6.如图,点是平分线上的一点,,垂足为D,若,则点到边的距离是( )
A. B.3 C.5 D.4
7.如图,AB=AC,∠B=30°,AC的垂直平分线MN交BC于点D,则∠DAC=( )
A.30° B.40° C.60° D.120°
8.如图,在△ABC中,BC=8,AB的垂直平分线分别交AB、AC于点D、E,△BCE的周长为18,则AC的长等于( )
A.12 B.10 C.8 D.6
9.如图,在学习了轴对称后,小明在课外研究三角板时发现“两块完全相同的含有的三角板可以拼成一个等边三角形”,请你帮他解决以下问题:在直角中,,,点分别在斜边和直角边上,则的最小值是( )
A. B. C. D.
10.如图,在中,,AD平分,,,那么点D到直线AB的距离是( )
A.2cm B.4cm C.6cm D.10cm
11.如图,在四边形ABCD中,,DE平分交BC于点E,若,,则CD的长是( )
A.2cm B.4cm C.6cm D.8cm
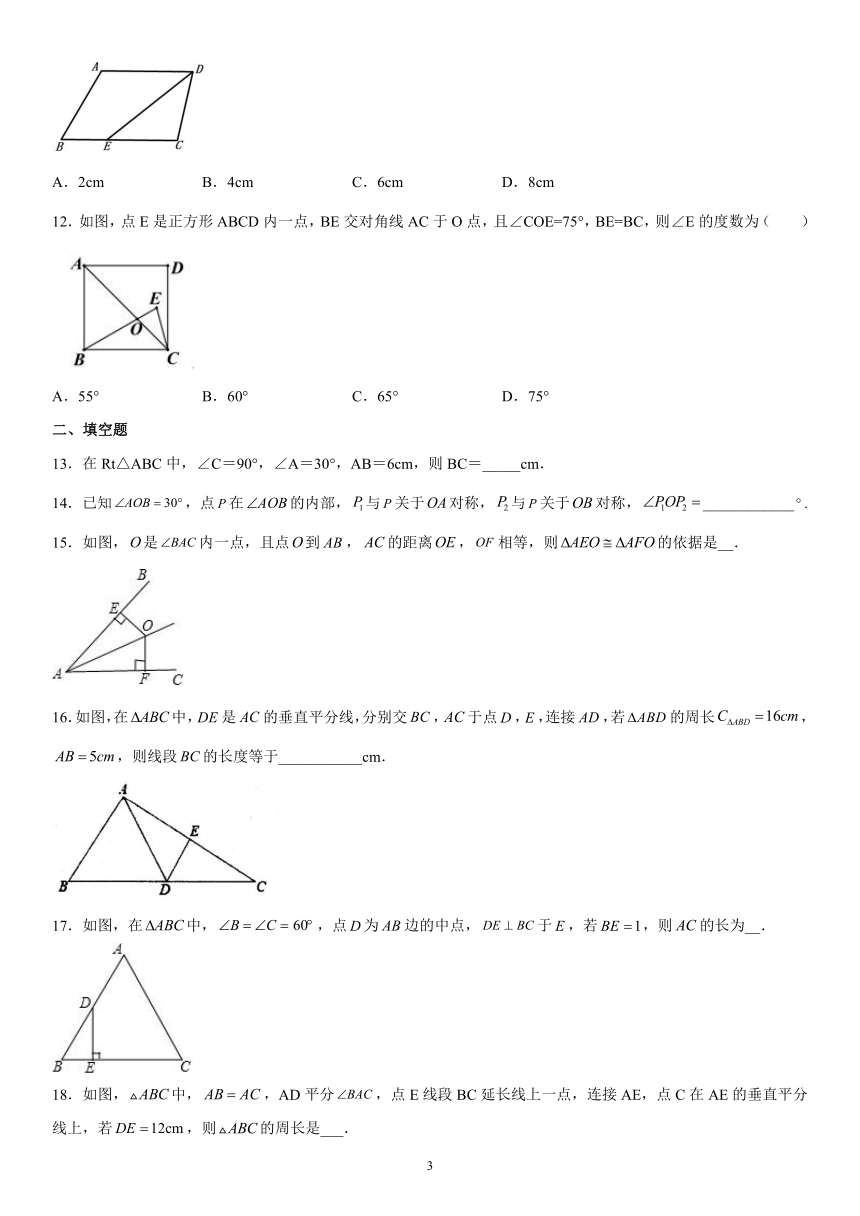
12.如图,点E是正方形ABCD内一点,BE交对角线AC于O点,且∠COE=75°,BE=BC,则∠E的度数为( )
A.55° B.60° C.65° D.75°
二、填空题
13.在Rt△ABC中,∠C=90°,∠A=30°,AB=6cm,则BC=_____cm.
14.已知,点在的内部,与关于对称,与关于对称,____________.
15.如图,是内一点,且点到,的距离,相等,则的依据是__.
16.如图,在中,是的垂直平分线,分别交,于点,,连接,若的周长,,则线段的长度等于___________cm.
17.如图,在中,,点为边的中点,于,若,则的长为__.
18.如图,中,,AD平分,点E线段BC延长线上一点,连接AE,点C在AE的垂直平分线上,若,则的周长是___.
19.如图,△ABC中,AB=AC,BC=4,△ABC的面积为20,腰AC的垂直平分线EF分别交边AC,AB于点E,F,若D为BC边的中点,M为线段EF上一动点,则△CDM的周长的最小值为__________.
20.如图,BD平分∠ABC,CD⊥BD,D为垂足,∠C=55°,则∠ABC的度数是_______.
三、解答题
21.如图,把长方形纸片沿折叠,使点落在边上的点处,点落在点处.
(1)试说明;
(2)设,,,试猜想,,之间的关系,并说明理由.
22.如图所示有一张图纸被损坏,上面两个标志点,清晰,而主要建筑标志点)破损.
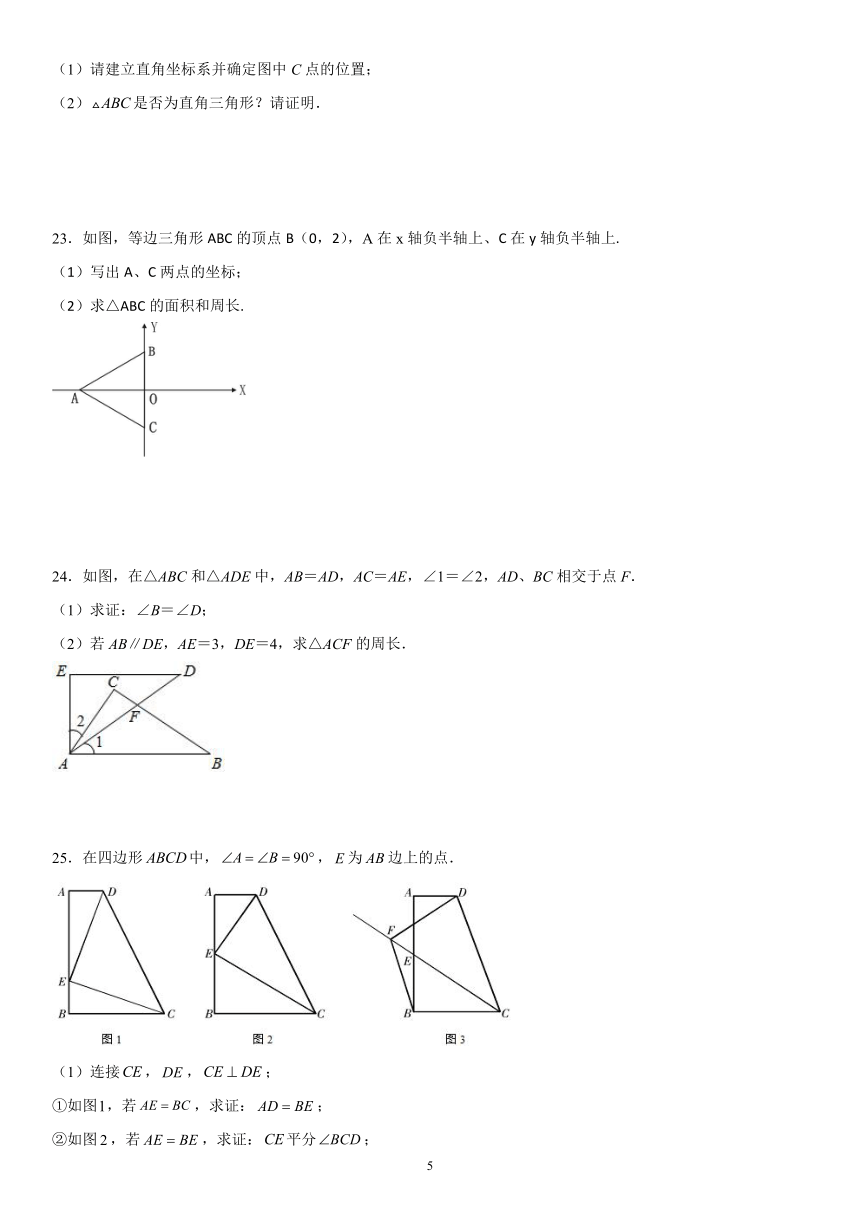
(1)请建立直角坐标系并确定图中C点的位置;
(2)是否为直角三角形?请证明.
23.如图,等边三角形ABC的顶点B(0,2),A在x轴负半轴上、C在y轴负半轴上.
(1)写出A、C两点的坐标;
(2)求△ABC的面积和周长.
24.如图,在△ABC和△ADE中,AB=AD,AC=AE,∠1=∠2,AD、BC相交于点F.
(1)求证:∠B=∠D;
(2)若AB∥DE,AE=3,DE=4,求△ACF的周长.
25.在四边形中,,为边上的点.
(1)连接,,;
①如图,若,求证:;
②如图,若,求证:平分;
(2)如图,是的平分线上的点,连接,,若,,,求的长.
26.如果两个等边三角形△ABD和△BCE,连接AE与CD.
证明:(1)AE与DC的夹角为60°;
(2)AE与DC的交点设为H,BH平分∠AHC.
27.等边△ABD和等边△BCE如图所示,连接AE与CD.
证明:(1)AE=DC;
(2)AE与DC的夹角为60°;
(3)AE延长线与DC的交点设为H,求证:BH平分∠AHC.
参考答案:
1.A 2.C 3.C 4.C 5.C 6.B 7.A 8.B 9.C 10.B 11.C 12.D
13.3
14.
15.HL
16.
17.4
18.24cm
19.12
20.70°
21.(1)由折叠的性质 ,得,,
在长方形纸片中,,所以,
所以,所以,
所以.
(2),,之间的关系是.理由如下:
由(1)知,由折叠的性质,得,,.
在中,,
所以,所以.
22.解:(1)
:
(2)不是直角三角形.
证明:∵,,,
∴,
即不是直角三角形.
23.解:(1)等边△ABC的顶点B的坐标(0,2),A在x轴负半轴上、C在y轴负半轴上B、C在y轴上.
x轴垂直平分BC,A0是BC边上的高,
OA平分∠BAC,
∠BAO=30,
OA=tan30OA=2= ,
A(-,0),C(0,-2) ;
(2)B(-,0),C(0,-2) ;,
BC=4,
=== ,周长=3BC=34=12 ;
24.解:(1)证明:∵,∴,
∴,
则在和中,
∴
∴
(2)∵ ∴
又∵ ∴,
则, 是等腰三角形,∴
又∵
则 ,
∴的周长.
25.(1)①证明:,
,,
,
在和中
,,,
,
.
②证明:延长交的延长线于点,
,
,,
,
,
,
,
,
,
,
,
平分.
(2)解法1:如图,过点分别作,,分别交及的延长线于点,.
平分,
,
又,,
,
在和中
,,,
,
,,
在和中
,,,
,
设,
,,
,,
,
,
,
,
在和中
,,,
.
解法2:如图,在上截取,
,,
,
在和中
,,,
,
,
,
,
过作,垂足为,
,
,
在和中
.
26.证明:(1)∵和是等边三角形
∴,,
∴
在和中,
∴
∴,
∵
∴在中,
;
(2)过点分别作,,垂足为点、,如图:
∵由(1)知:
∴,
∴
∴
∵,
∴点在的平分线上,
∴平分.
27.证明:(1)∵△ABD和△BCE都是等边三角形,
∴AB=DB,EB=CB,∠ABD=∠EBC
∴∠ABE=∠DBC
∴在△ABE和△DBC中
∴△ABE≌△DBC(SAS)
∴AE=DC;
(2)∵△ABE≌△DBC
∴∠BAE=∠BDC
又∵∠BAE+∠HAD+∠ADB=120°
∴∠BDC+∠HAD+∠ADB=120°
∴△ADH中,∠AHD=180°﹣120°=60°
即AE与DC的夹角为60°;
(3)过B作BF⊥DC于F,BG⊥AH于G,如图:
∵△ABE≌△DBC
∴S△ABE=S△DBC,即AE×BGDC×BF
∵AE=DC
∴BG=BF
∵BF⊥DC于F,BG⊥AH于G
∴BH平分∠AHC.
答案第1页,共2页
姓名:___________班级:___________
一、单选题
1.如图,已知∠ABC,小彬借助一把没有刻度且等宽的直尺,按如图的方法画出了∠ABC的平分线BP.他这样做的依据是( )
A.在一个角的内部,且到角两边的距离相等的点在这个角的平分线上
B.角平分线上的点到这个角两边的距离相等
C.三角形三条角平分线的交点到三条边的距离相等
D.测量垂直平分线上的点到这条线段的距离相等
2.如图,在△PAB中,PA=PB,M,N,K分别是PA,PB,AB上的点,且AM=BK,BN=AK,若∠MKN=42°,则∠P的度数为( )
A.44° B.66° C.96° D.92°
3.下列能断定△ABC为等腰三角形的是( )
A.∠A=40°,∠B=50° B.∠A=2∠B=70°
C.∠A=40°,∠B=70° D.AB=3,BC=6,周长为14
4.如图,在中,,为中点.若,,则的度数为( )
A. B. C. D.
5.如图,已知的面积为,为的平分线,于点,则的面积为( ).
A. B. C. D.
6.如图,点是平分线上的一点,,垂足为D,若,则点到边的距离是( )
A. B.3 C.5 D.4
7.如图,AB=AC,∠B=30°,AC的垂直平分线MN交BC于点D,则∠DAC=( )
A.30° B.40° C.60° D.120°
8.如图,在△ABC中,BC=8,AB的垂直平分线分别交AB、AC于点D、E,△BCE的周长为18,则AC的长等于( )
A.12 B.10 C.8 D.6
9.如图,在学习了轴对称后,小明在课外研究三角板时发现“两块完全相同的含有的三角板可以拼成一个等边三角形”,请你帮他解决以下问题:在直角中,,,点分别在斜边和直角边上,则的最小值是( )
A. B. C. D.
10.如图,在中,,AD平分,,,那么点D到直线AB的距离是( )
A.2cm B.4cm C.6cm D.10cm
11.如图,在四边形ABCD中,,DE平分交BC于点E,若,,则CD的长是( )
A.2cm B.4cm C.6cm D.8cm
12.如图,点E是正方形ABCD内一点,BE交对角线AC于O点,且∠COE=75°,BE=BC,则∠E的度数为( )
A.55° B.60° C.65° D.75°
二、填空题
13.在Rt△ABC中,∠C=90°,∠A=30°,AB=6cm,则BC=_____cm.
14.已知,点在的内部,与关于对称,与关于对称,____________.
15.如图,是内一点,且点到,的距离,相等,则的依据是__.
16.如图,在中,是的垂直平分线,分别交,于点,,连接,若的周长,,则线段的长度等于___________cm.
17.如图,在中,,点为边的中点,于,若,则的长为__.
18.如图,中,,AD平分,点E线段BC延长线上一点,连接AE,点C在AE的垂直平分线上,若,则的周长是___.
19.如图,△ABC中,AB=AC,BC=4,△ABC的面积为20,腰AC的垂直平分线EF分别交边AC,AB于点E,F,若D为BC边的中点,M为线段EF上一动点,则△CDM的周长的最小值为__________.
20.如图,BD平分∠ABC,CD⊥BD,D为垂足,∠C=55°,则∠ABC的度数是_______.
三、解答题
21.如图,把长方形纸片沿折叠,使点落在边上的点处,点落在点处.
(1)试说明;
(2)设,,,试猜想,,之间的关系,并说明理由.
22.如图所示有一张图纸被损坏,上面两个标志点,清晰,而主要建筑标志点)破损.
(1)请建立直角坐标系并确定图中C点的位置;
(2)是否为直角三角形?请证明.
23.如图,等边三角形ABC的顶点B(0,2),A在x轴负半轴上、C在y轴负半轴上.
(1)写出A、C两点的坐标;
(2)求△ABC的面积和周长.
24.如图,在△ABC和△ADE中,AB=AD,AC=AE,∠1=∠2,AD、BC相交于点F.
(1)求证:∠B=∠D;
(2)若AB∥DE,AE=3,DE=4,求△ACF的周长.
25.在四边形中,,为边上的点.
(1)连接,,;
①如图,若,求证:;
②如图,若,求证:平分;
(2)如图,是的平分线上的点,连接,,若,,,求的长.
26.如果两个等边三角形△ABD和△BCE,连接AE与CD.
证明:(1)AE与DC的夹角为60°;
(2)AE与DC的交点设为H,BH平分∠AHC.
27.等边△ABD和等边△BCE如图所示,连接AE与CD.
证明:(1)AE=DC;
(2)AE与DC的夹角为60°;
(3)AE延长线与DC的交点设为H,求证:BH平分∠AHC.
参考答案:
1.A 2.C 3.C 4.C 5.C 6.B 7.A 8.B 9.C 10.B 11.C 12.D
13.3
14.
15.HL
16.
17.4
18.24cm
19.12
20.70°
21.(1)由折叠的性质 ,得,,
在长方形纸片中,,所以,
所以,所以,
所以.
(2),,之间的关系是.理由如下:
由(1)知,由折叠的性质,得,,.
在中,,
所以,所以.
22.解:(1)
:
(2)不是直角三角形.
证明:∵,,,
∴,
即不是直角三角形.
23.解:(1)等边△ABC的顶点B的坐标(0,2),A在x轴负半轴上、C在y轴负半轴上B、C在y轴上.
x轴垂直平分BC,A0是BC边上的高,
OA平分∠BAC,
∠BAO=30,
OA=tan30OA=2= ,
A(-,0),C(0,-2) ;
(2)B(-,0),C(0,-2) ;,
BC=4,
=== ,周长=3BC=34=12 ;
24.解:(1)证明:∵,∴,
∴,
则在和中,
∴
∴
(2)∵ ∴
又∵ ∴,
则, 是等腰三角形,∴
又∵
则 ,
∴的周长.
25.(1)①证明:,
,,
,
在和中
,,,
,
.
②证明:延长交的延长线于点,
,
,,
,
,
,
,
,
,
,
,
平分.
(2)解法1:如图,过点分别作,,分别交及的延长线于点,.
平分,
,
又,,
,
在和中
,,,
,
,,
在和中
,,,
,
设,
,,
,,
,
,
,
,
在和中
,,,
.
解法2:如图,在上截取,
,,
,
在和中
,,,
,
,
,
,
过作,垂足为,
,
,
在和中
.
26.证明:(1)∵和是等边三角形
∴,,
∴
在和中,
∴
∴,
∵
∴在中,
;
(2)过点分别作,,垂足为点、,如图:
∵由(1)知:
∴,
∴
∴
∵,
∴点在的平分线上,
∴平分.
27.证明:(1)∵△ABD和△BCE都是等边三角形,
∴AB=DB,EB=CB,∠ABD=∠EBC
∴∠ABE=∠DBC
∴在△ABE和△DBC中
∴△ABE≌△DBC(SAS)
∴AE=DC;
(2)∵△ABE≌△DBC
∴∠BAE=∠BDC
又∵∠BAE+∠HAD+∠ADB=120°
∴∠BDC+∠HAD+∠ADB=120°
∴△ADH中,∠AHD=180°﹣120°=60°
即AE与DC的夹角为60°;
(3)过B作BF⊥DC于F,BG⊥AH于G,如图:
∵△ABE≌△DBC
∴S△ABE=S△DBC,即AE×BGDC×BF
∵AE=DC
∴BG=BF
∵BF⊥DC于F,BG⊥AH于G
∴BH平分∠AHC.
答案第1页,共2页
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
