2021-2022学年北师大版七年级数学下册2.2探索直线平行的条件同步练习(Word版含答案)
文档属性
| 名称 | 2021-2022学年北师大版七年级数学下册2.2探索直线平行的条件同步练习(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 239.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-21 15:28:25 | ||
图片预览



文档简介
2.2 探索直线平行的条件 北师大版
一、单选题
1.已知如图直线a,b被直线c所截,下列条件能判断a∥b的是( )
A.∠1=∠2 B.∠2=∠3 C.∠1=∠4 D.∠2+∠5=180°
2.在同一平面内三条不同的直线a、b、c,其中a⊥b,a⊥c,则直线b与直线c的关系是( )
A.相交 B.平行 C.垂直 D.不确定
3.若两平行直线被第三条直线所截,则一对同旁内角的角平分线的关系是( )
A.互相垂直 B.互相平行 C.相交但不垂直 D.以上都不对
4.如图,直线a,b被直线c所截,现给出下列四个条件:(1);(2);(3);(4),其中能判定的条件的序号是( )
A.(1),(2) B.(1),(3) C.(1),(4) D.(3),(4)
5.下列说法正确的是( )
A.、、是直线,若,,则
B.、、是直线,若,,则
C.、、是直线,若,,则
D.、、是直线,若,,则
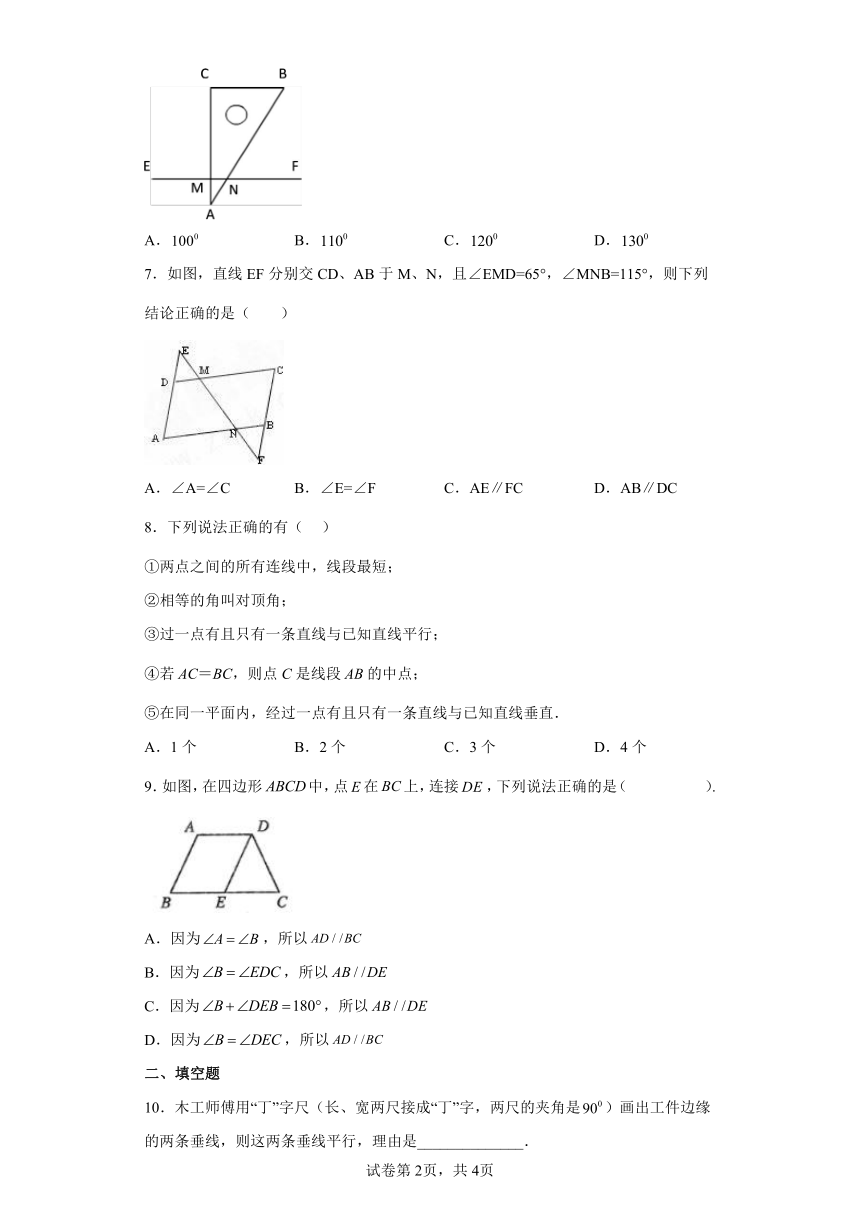
6.如图,一根直尺EF压在三角板 的角∠BAC上,欲使CB∥EF,则应使∠ENB的度数为( )
A. B. C. D.
7.如图,直线EF分别交CD、AB于M、N,且∠EMD=65°,∠MNB=115°,则下列结论正确的是( )
A.∠A=∠C B.∠E=∠F C.AE∥FC D.AB∥DC
8.下列说法正确的有( )
①两点之间的所有连线中,线段最短;
②相等的角叫对顶角;
③过一点有且只有一条直线与已知直线平行;
④若AC=BC,则点C是线段AB的中点;
⑤在同一平面内,经过一点有且只有一条直线与已知直线垂直.
A.1个 B.2个 C.3个 D.4个
9.如图,在四边形中,点在上,连接,下列说法正确的是( ).
A.因为,所以
B.因为,所以
C.因为,所以
D.因为,所以
二、填空题
10.木工师傅用“丁”字尺(长、宽两尺接成“丁”字,两尺的夹角是)画出工件边缘的两条垂线,则这两条垂线平行,理由是______________.
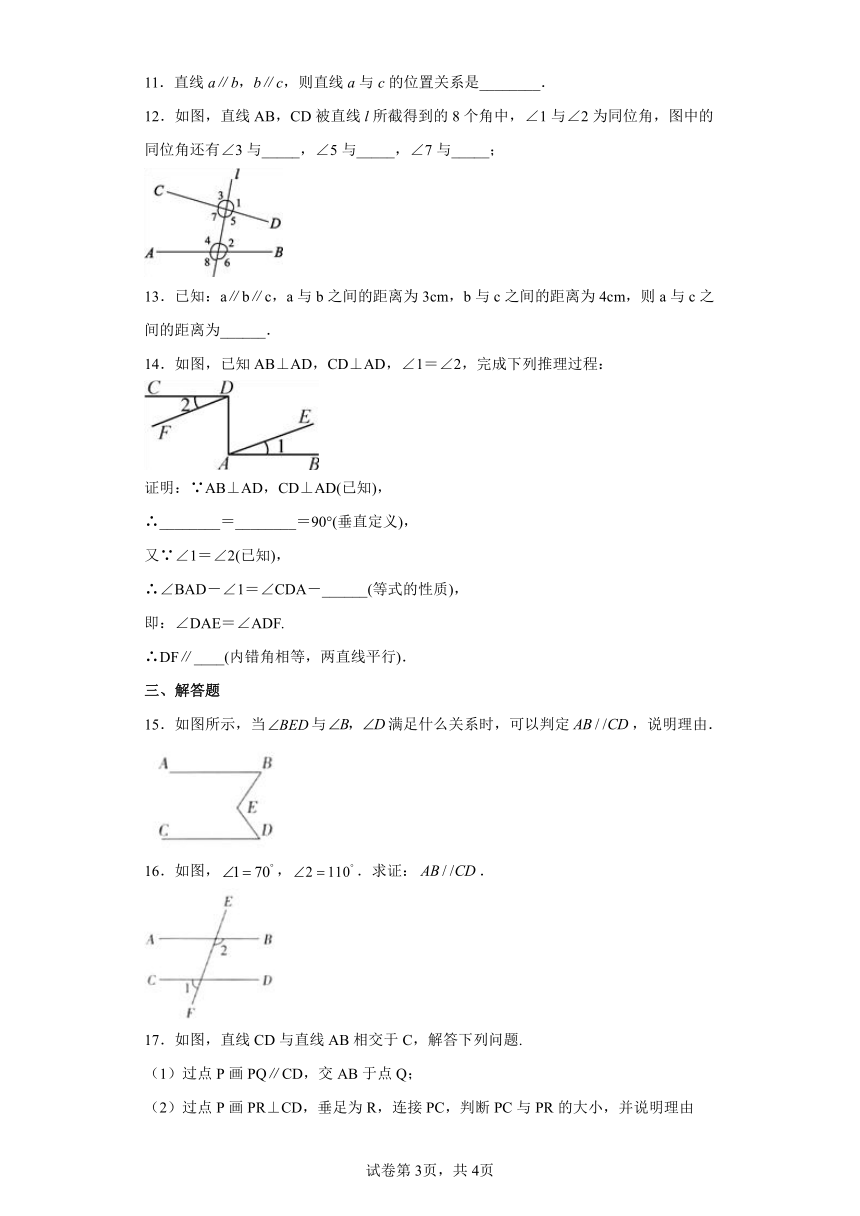
11.直线a∥b,b∥c,则直线a与c的位置关系是________.
12.如图,直线AB,CD被直线l所截得到的8个角中,∠1与∠2为同位角,图中的同位角还有∠3与_____,∠5与_____,∠7与_____;
13.已知:a∥b∥c,a与b之间的距离为3cm,b与c之间的距离为4cm,则a与c之间的距离为______.
14.如图,已知AB⊥AD,CD⊥AD,∠1=∠2,完成下列推理过程:
证明:∵AB⊥AD,CD⊥AD(已知),
∴________=________=90°(垂直定义),
又∵∠1=∠2(已知),
∴∠BAD-∠1=∠CDA-______(等式的性质),
即:∠DAE=∠ADF.
∴DF∥____(内错角相等,两直线平行).
三、解答题
15.如图所示,当与满足什么关系时,可以判定,说明理由.
16.如图,,.求证:.
17.如图,直线CD与直线AB相交于C,解答下列问题.
(1)过点P画PQ∥CD,交AB于点Q;
(2)过点P画PR⊥CD,垂足为R,连接PC,判断PC与PR的大小,并说明理由
18.如图都是4×4的网格正方形,且每个小正方形边长都为1,请你利用无刻度直尺,按下列要求画图(保留作图痕迹,不写作法).
(1)在图1中,画直线AB∥CD,且AB与CD之间的距离为2.
(2)在图2中,画一个直角三角形,使三角形的顶点都在格点上,且面积为3.
试卷第1页,共3页
试卷第2页,共2页
参考答案:
1.A
【解析】
试题解析:∵∠1=∠2,
∴a∥b;
故选A.
2.B
【解析】
解:∵a⊥b,a⊥c
∴a∥c.
故选:B.
3.A
【解析】
∵AB∥CD,
∴∠BEF+∠DFE=180°,
∵EG与FG分别是∠BEF与∠DFE的角平分线,
∴∠1=∠BEF,∠2=∠DFE,
∴∠1+∠2=∠BEF +∠DFE =(∠BEF+∠DFE)=90°,
∴∠EGF=90°,
∴EG⊥FG.
故选:A.
4.A
【解析】
解:
故(1)可判定;
故(2)可判定;
,不能判定故(3)不能判定;
,不能判定故(4)不能判定.
故选:
5.D
【解析】
解:先根据要求画出图形,图形如下图所示:
根据所画图形可知:D正确.
故选:D
6.C
【解析】
解:因为三角板含有30°的角,所以∠B=60°,当∠ENB+∠B=180°时,根据“同旁内角互补,两直线平行”,可使CB∥EF,此时∠ENB=180°-∠B=180°-60°=.
故选C.
7.D
【解析】
∵∠EMD=65°,∠MNB=115°,
∴∠CMN=∠EMD=65°,
∴∠CMN+∠MNB=180°,
∴AB∥DC
故选D.
8.B
【解析】
解:①两点之间的所有连线中,线段最短,正确;
②相等的角不一定是对顶角,但对顶角相等,故本小题错误;
③过直线外一点有且仅有一条直线与已知直线平行,故本小题错误;
④若AC=BC,且A、B、C三点共线,则点C是线段AB的中点,否则不是,故本小题错误,
⑤在同一平面内,过一点有且只有一条直线与已知直线垂直,正确;
所以,正确的结论有①⑤共2个.
故选:B.
9.C
【解析】
A. 因为和是同旁内角,所以根据不能得到,故A选项错误;
B. 因为和不是同位角也不是内错角,所以根据不能得到,故B选项错误;
C. 因为和是同旁内角,所以根据可以得到,故本选项正确;
D. 和虽然是同位角,但根据只可以得出,故本选项错误.
故本题选C.
10.同位角相等,两直线平行;或在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行
【解析】
解法一:∵∠1=∠2=90°,
∴l′∥l(同位角相等,两直线平行).
则两条垂线平行的理由为:同位角相等,两直线平行.
解法二:根据同一平面内,垂直于同一条直线的两条直线平行可知,两条垂线平行.
故答案为同位角相等,两直线平行;或在同一平面内,垂直于同一条直线的两条直线平行可知,两条垂线平行.
11.平行
【解析】
解:∵直线a∥b,b∥c,
∴a∥c,
则直线a与c的位置关系是平行,
故答案为:平行.
12. ∠4 ∠6 ∠8
【解析】
由同位角定义知:∠3与∠4、∠5与∠6、∠7与∠8是同位角,
故答案为:∠4、∠6、∠8
13.7cm或1cm.
【解析】
①如图1,当b在a、c之间时,
a与c之间距离为3+4=7(cm);
②如图2,c在b、a之间时,
a与c之间距离为4﹣3=1(cm);
故答案是:7cm或1cm.
14.∠DAB ,∠ADC ,∠2 ,AE.
【解析】
试题解析:证明: (已知),
(垂直定义).
又 (已知),
(等式的性质),
即
(内错角相等,两直线平行).
故答案分别是:
15.当时,,见解析.
【解析】
解:当时,.
理由如下:
如图,连接.
在中,.
∵(已知),
∴(等量代换),
即.
∴(同旁内角互补,两直线平行).
16.见解析
【解析】
证明:如图,∵(已知),
∴(对顶角相等),
∴,
∴(同旁内角互补,两直线平行).
17.(1)见解析;(2)作图见解析;PC>PR;垂线段最短
【解析】
解:(1)如图,PQ∥CD,交AB于点Q;
(2)如图PR⊥CD,
PC与PR的大小为:PC>PR,理由是:垂线段最短.
18.(1)见解析;(2)见解析.
【解析】
解:(1)图1中AB、CD为所画.
(2)图2中△ABC为所画.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.已知如图直线a,b被直线c所截,下列条件能判断a∥b的是( )
A.∠1=∠2 B.∠2=∠3 C.∠1=∠4 D.∠2+∠5=180°
2.在同一平面内三条不同的直线a、b、c,其中a⊥b,a⊥c,则直线b与直线c的关系是( )
A.相交 B.平行 C.垂直 D.不确定
3.若两平行直线被第三条直线所截,则一对同旁内角的角平分线的关系是( )
A.互相垂直 B.互相平行 C.相交但不垂直 D.以上都不对
4.如图,直线a,b被直线c所截,现给出下列四个条件:(1);(2);(3);(4),其中能判定的条件的序号是( )
A.(1),(2) B.(1),(3) C.(1),(4) D.(3),(4)
5.下列说法正确的是( )
A.、、是直线,若,,则
B.、、是直线,若,,则
C.、、是直线,若,,则
D.、、是直线,若,,则
6.如图,一根直尺EF压在三角板 的角∠BAC上,欲使CB∥EF,则应使∠ENB的度数为( )
A. B. C. D.
7.如图,直线EF分别交CD、AB于M、N,且∠EMD=65°,∠MNB=115°,则下列结论正确的是( )
A.∠A=∠C B.∠E=∠F C.AE∥FC D.AB∥DC
8.下列说法正确的有( )
①两点之间的所有连线中,线段最短;
②相等的角叫对顶角;
③过一点有且只有一条直线与已知直线平行;
④若AC=BC,则点C是线段AB的中点;
⑤在同一平面内,经过一点有且只有一条直线与已知直线垂直.
A.1个 B.2个 C.3个 D.4个
9.如图,在四边形中,点在上,连接,下列说法正确的是( ).
A.因为,所以
B.因为,所以
C.因为,所以
D.因为,所以
二、填空题
10.木工师傅用“丁”字尺(长、宽两尺接成“丁”字,两尺的夹角是)画出工件边缘的两条垂线,则这两条垂线平行,理由是______________.
11.直线a∥b,b∥c,则直线a与c的位置关系是________.
12.如图,直线AB,CD被直线l所截得到的8个角中,∠1与∠2为同位角,图中的同位角还有∠3与_____,∠5与_____,∠7与_____;
13.已知:a∥b∥c,a与b之间的距离为3cm,b与c之间的距离为4cm,则a与c之间的距离为______.
14.如图,已知AB⊥AD,CD⊥AD,∠1=∠2,完成下列推理过程:
证明:∵AB⊥AD,CD⊥AD(已知),
∴________=________=90°(垂直定义),
又∵∠1=∠2(已知),
∴∠BAD-∠1=∠CDA-______(等式的性质),
即:∠DAE=∠ADF.
∴DF∥____(内错角相等,两直线平行).
三、解答题
15.如图所示,当与满足什么关系时,可以判定,说明理由.
16.如图,,.求证:.
17.如图,直线CD与直线AB相交于C,解答下列问题.
(1)过点P画PQ∥CD,交AB于点Q;
(2)过点P画PR⊥CD,垂足为R,连接PC,判断PC与PR的大小,并说明理由
18.如图都是4×4的网格正方形,且每个小正方形边长都为1,请你利用无刻度直尺,按下列要求画图(保留作图痕迹,不写作法).
(1)在图1中,画直线AB∥CD,且AB与CD之间的距离为2.
(2)在图2中,画一个直角三角形,使三角形的顶点都在格点上,且面积为3.
试卷第1页,共3页
试卷第2页,共2页
参考答案:
1.A
【解析】
试题解析:∵∠1=∠2,
∴a∥b;
故选A.
2.B
【解析】
解:∵a⊥b,a⊥c
∴a∥c.
故选:B.
3.A
【解析】
∵AB∥CD,
∴∠BEF+∠DFE=180°,
∵EG与FG分别是∠BEF与∠DFE的角平分线,
∴∠1=∠BEF,∠2=∠DFE,
∴∠1+∠2=∠BEF +∠DFE =(∠BEF+∠DFE)=90°,
∴∠EGF=90°,
∴EG⊥FG.
故选:A.
4.A
【解析】
解:
故(1)可判定;
故(2)可判定;
,不能判定故(3)不能判定;
,不能判定故(4)不能判定.
故选:
5.D
【解析】
解:先根据要求画出图形,图形如下图所示:
根据所画图形可知:D正确.
故选:D
6.C
【解析】
解:因为三角板含有30°的角,所以∠B=60°,当∠ENB+∠B=180°时,根据“同旁内角互补,两直线平行”,可使CB∥EF,此时∠ENB=180°-∠B=180°-60°=.
故选C.
7.D
【解析】
∵∠EMD=65°,∠MNB=115°,
∴∠CMN=∠EMD=65°,
∴∠CMN+∠MNB=180°,
∴AB∥DC
故选D.
8.B
【解析】
解:①两点之间的所有连线中,线段最短,正确;
②相等的角不一定是对顶角,但对顶角相等,故本小题错误;
③过直线外一点有且仅有一条直线与已知直线平行,故本小题错误;
④若AC=BC,且A、B、C三点共线,则点C是线段AB的中点,否则不是,故本小题错误,
⑤在同一平面内,过一点有且只有一条直线与已知直线垂直,正确;
所以,正确的结论有①⑤共2个.
故选:B.
9.C
【解析】
A. 因为和是同旁内角,所以根据不能得到,故A选项错误;
B. 因为和不是同位角也不是内错角,所以根据不能得到,故B选项错误;
C. 因为和是同旁内角,所以根据可以得到,故本选项正确;
D. 和虽然是同位角,但根据只可以得出,故本选项错误.
故本题选C.
10.同位角相等,两直线平行;或在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行
【解析】
解法一:∵∠1=∠2=90°,
∴l′∥l(同位角相等,两直线平行).
则两条垂线平行的理由为:同位角相等,两直线平行.
解法二:根据同一平面内,垂直于同一条直线的两条直线平行可知,两条垂线平行.
故答案为同位角相等,两直线平行;或在同一平面内,垂直于同一条直线的两条直线平行可知,两条垂线平行.
11.平行
【解析】
解:∵直线a∥b,b∥c,
∴a∥c,
则直线a与c的位置关系是平行,
故答案为:平行.
12. ∠4 ∠6 ∠8
【解析】
由同位角定义知:∠3与∠4、∠5与∠6、∠7与∠8是同位角,
故答案为:∠4、∠6、∠8
13.7cm或1cm.
【解析】
①如图1,当b在a、c之间时,
a与c之间距离为3+4=7(cm);
②如图2,c在b、a之间时,
a与c之间距离为4﹣3=1(cm);
故答案是:7cm或1cm.
14.∠DAB ,∠ADC ,∠2 ,AE.
【解析】
试题解析:证明: (已知),
(垂直定义).
又 (已知),
(等式的性质),
即
(内错角相等,两直线平行).
故答案分别是:
15.当时,,见解析.
【解析】
解:当时,.
理由如下:
如图,连接.
在中,.
∵(已知),
∴(等量代换),
即.
∴(同旁内角互补,两直线平行).
16.见解析
【解析】
证明:如图,∵(已知),
∴(对顶角相等),
∴,
∴(同旁内角互补,两直线平行).
17.(1)见解析;(2)作图见解析;PC>PR;垂线段最短
【解析】
解:(1)如图,PQ∥CD,交AB于点Q;
(2)如图PR⊥CD,
PC与PR的大小为:PC>PR,理由是:垂线段最短.
18.(1)见解析;(2)见解析.
【解析】
解:(1)图1中AB、CD为所画.
(2)图2中△ABC为所画.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
