2021-2022学年人教版七年级数学下册5.1相交线练习(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版七年级数学下册5.1相交线练习(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 369.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-21 15:28:27 | ||
图片预览




文档简介
5.1 相交线
一、单选题
1.如图,AB、CD、EF相交于点O,且CD⊥AB,那么∠1和∠2的关系是( )
A.∠1+∠2=180° B.∠1+∠2=90° C.∠1=∠2 D.无法确定
2.如图,直线、交于点,则下列结论中一定成立的是( )
A. B.
C. D.
3.如图,的邻补角是( )
B.和
C. D.和
4.如图所示,是平角,是射线,、分别是、的角平分线,若,则的度数为( )
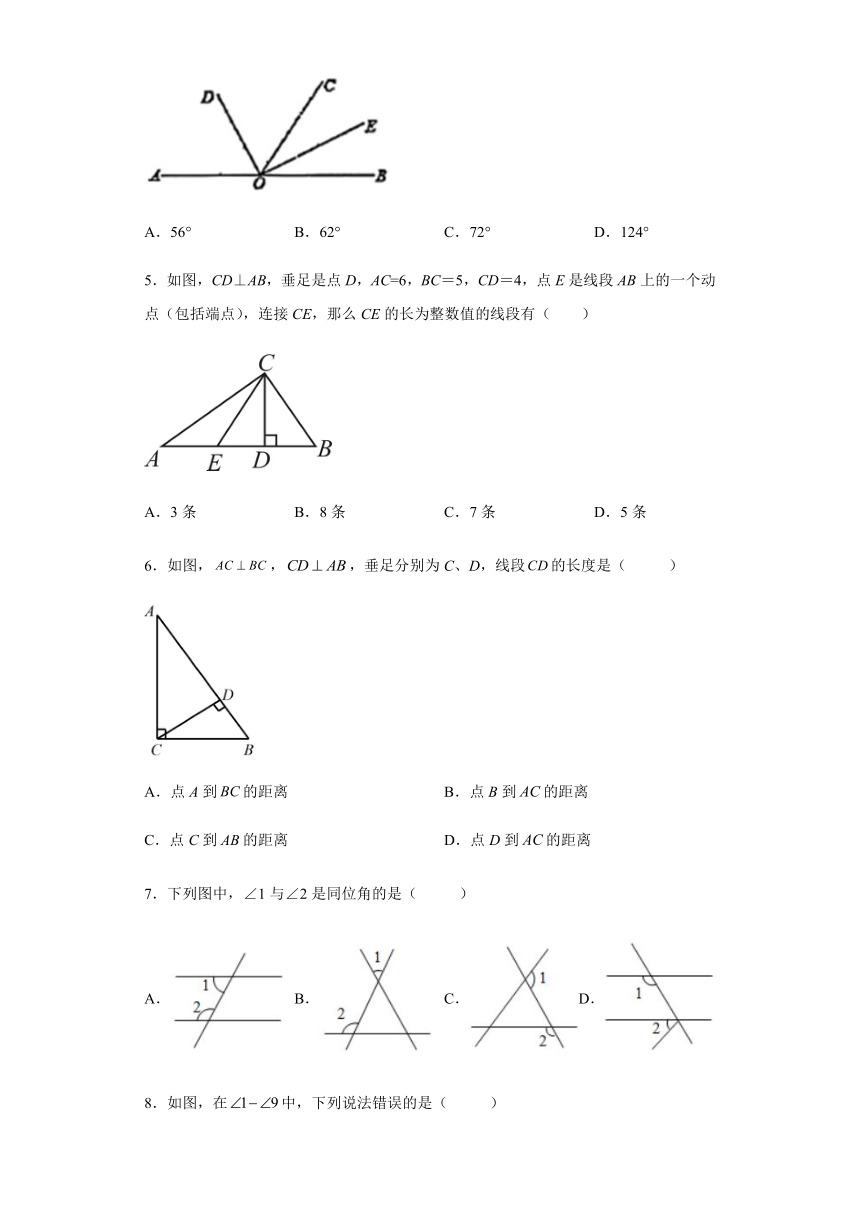
A.56° B.62° C.72° D.124°
5.如图,CD⊥AB,垂足是点D,AC=6,BC=5,CD=4,点E是线段AB上的一个动点(包括端点),连接CE,那么CE的长为整数值的线段有( )
A.3条 B.8条 C.7条 D.5条
6.如图,,,垂足分别为C、D,线段的长度是( )
A.点A到的距离 B.点B到的距离
C.点C到的距离 D.点D到的距离
7.下列图中,∠1与∠2是同位角的是( )
A. B. C.D.
8.如图,在中,下列说法错误的是( )
A.和是一对内错角 B.和是一对同位角
C.和是一对同旁内角 D.和是一对内错角
9.观察下列图形并阅读图形下方的文字,像这样,条直线相交,交点的个数最多为( )
A. B. C. D.
10.如图,直线,相交于点,,,平分,给出下列结论:①当时,;②为的平分线;③若时,;④.其中正确的结论有( )
A.4个 B.3个 C.2个 D.1个
二、填空题
11.射线OA表示的方位角是南偏东,射线OB与射线OA构成平角,那么射线OB所表示的方位角是___.
12.如图,OE⊥AB于点O,OC为∠AOE内的一条射线,OD是OC的反射向延长线,OF平分∠AOD,∠COE=20°,则∠COF的度数为 _____.
13.如图,直线AC和FD相交于点B,下列判断:①∠GBD和∠HCE是同位角;②∠ABD和∠ACH是同位角;③∠FBC和∠ACE是内错角;④∠FBC和∠HCE是内错角;⑤∠GBC和∠BCE是同旁内角.其中正确的是____.(填序号)
14.如图,点O在直线AB上,过O作射线OC,∠BOC=100°,一直角三角板的直角顶点与点O重合,边OM与OB重合,边ON在直线AB的下方.若三角板绕点O按每秒10°的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,则t的值为________.
解答题
15.如图,直线DE,BC被直线AB所截.
(1)∠1和∠2,∠1和∠3,∠1和∠4各是什么位置关系的角?
(2)如果∠1=∠4,那么∠1和∠2相等吗?∠1和∠3互补吗?为什么?
16.补充下列证明,并在括号内填上推理依据.
已知:如图,∠AOB+∠BOC=180°,OE平分∠AOB,OF平分∠BOC.求证:OE⊥OF.
证明:∵OE平分∠AOB,OF平分∠BOC,( )
∴∠1=∠AOB,∠2=∠BOC.( )
又∵∠AOB+∠BOC=180°,( )
∴∠1+∠2=(∠AOB+∠BOC)=______°( )
∴OE⊥OF.( )
17.如图,直线AB,CD相交于点O,射线OE把分成两部分.
(1)写出图中的对顶角___________,的补角是___________.
(2)已知,且,求的度数
18.如图,已知直线AB、CD相交于点O,OE平分∠BOD,OF平分∠COE,∠2:∠1=4:1,求∠AOF.
19.直角三角板的直角顶点在直线上,平分.
(1)在图1中,若,求;
(2)在图1中,若,________(用含的式子表示);
(3)将图1中的三角板绕顶点旋转至图2的位置,探究:写出和的度数之间的关系,并说明理由.
试卷第1页,共3页
答案
1.C
2.B
3.D
4.B
5.A
6.C
7.B
8.D
9.B
10.B
11.北偏西25°
12.125°
13.②③⑤
14.5或23
15.解:(1)∠1和∠2是内错角,∠1和∠3是同旁内角,∠1和∠4是同位角;
(2)∠1和∠2相等,∠1和∠3互补.
理由如下:
∵∠1=∠4,
∴DE∥BC,
∴∠1=∠2,∠1+∠3=180°
16.证明:∵OE平分∠AOB,OF平分∠BOC,(已知)
∴∠1=∠AOB,∠2=∠BOC.(角平分线的定义)
又∵∠AOB+∠BOC=180°,(已知)
∴∠1+∠2=(∠AOB+∠BOC)=90°.(等式性质)
∴OE⊥OF.(垂直的定义)
17.(1)解:根据题意得:的对顶角为;
的补角是,
故答案为:,;
(2)解:∵,,
∴,
∵,
∴,
∵,
∴.
18.解:设,则,
∵平分,
∴,
∵,
∴,
∴,
∵,
∴,
∵平分,
∴,
∵,
∴.
19.(1)解:∵,,
∴,,
又平分,
∴,
∴;
(2)解:∵,,
∴,,
又平分,
∴,
∴;
(3),理由如下:
∵点在上,
∴,
∵平分,
∴,
∵,
∴,
即:.
答案第1页,共2页
一、单选题
1.如图,AB、CD、EF相交于点O,且CD⊥AB,那么∠1和∠2的关系是( )
A.∠1+∠2=180° B.∠1+∠2=90° C.∠1=∠2 D.无法确定
2.如图,直线、交于点,则下列结论中一定成立的是( )
A. B.
C. D.
3.如图,的邻补角是( )
B.和
C. D.和
4.如图所示,是平角,是射线,、分别是、的角平分线,若,则的度数为( )
A.56° B.62° C.72° D.124°
5.如图,CD⊥AB,垂足是点D,AC=6,BC=5,CD=4,点E是线段AB上的一个动点(包括端点),连接CE,那么CE的长为整数值的线段有( )
A.3条 B.8条 C.7条 D.5条
6.如图,,,垂足分别为C、D,线段的长度是( )
A.点A到的距离 B.点B到的距离
C.点C到的距离 D.点D到的距离
7.下列图中,∠1与∠2是同位角的是( )
A. B. C.D.
8.如图,在中,下列说法错误的是( )
A.和是一对内错角 B.和是一对同位角
C.和是一对同旁内角 D.和是一对内错角
9.观察下列图形并阅读图形下方的文字,像这样,条直线相交,交点的个数最多为( )
A. B. C. D.
10.如图,直线,相交于点,,,平分,给出下列结论:①当时,;②为的平分线;③若时,;④.其中正确的结论有( )
A.4个 B.3个 C.2个 D.1个
二、填空题
11.射线OA表示的方位角是南偏东,射线OB与射线OA构成平角,那么射线OB所表示的方位角是___.
12.如图,OE⊥AB于点O,OC为∠AOE内的一条射线,OD是OC的反射向延长线,OF平分∠AOD,∠COE=20°,则∠COF的度数为 _____.
13.如图,直线AC和FD相交于点B,下列判断:①∠GBD和∠HCE是同位角;②∠ABD和∠ACH是同位角;③∠FBC和∠ACE是内错角;④∠FBC和∠HCE是内错角;⑤∠GBC和∠BCE是同旁内角.其中正确的是____.(填序号)
14.如图,点O在直线AB上,过O作射线OC,∠BOC=100°,一直角三角板的直角顶点与点O重合,边OM与OB重合,边ON在直线AB的下方.若三角板绕点O按每秒10°的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,则t的值为________.
解答题
15.如图,直线DE,BC被直线AB所截.
(1)∠1和∠2,∠1和∠3,∠1和∠4各是什么位置关系的角?
(2)如果∠1=∠4,那么∠1和∠2相等吗?∠1和∠3互补吗?为什么?
16.补充下列证明,并在括号内填上推理依据.
已知:如图,∠AOB+∠BOC=180°,OE平分∠AOB,OF平分∠BOC.求证:OE⊥OF.
证明:∵OE平分∠AOB,OF平分∠BOC,( )
∴∠1=∠AOB,∠2=∠BOC.( )
又∵∠AOB+∠BOC=180°,( )
∴∠1+∠2=(∠AOB+∠BOC)=______°( )
∴OE⊥OF.( )
17.如图,直线AB,CD相交于点O,射线OE把分成两部分.
(1)写出图中的对顶角___________,的补角是___________.
(2)已知,且,求的度数
18.如图,已知直线AB、CD相交于点O,OE平分∠BOD,OF平分∠COE,∠2:∠1=4:1,求∠AOF.
19.直角三角板的直角顶点在直线上,平分.
(1)在图1中,若,求;
(2)在图1中,若,________(用含的式子表示);
(3)将图1中的三角板绕顶点旋转至图2的位置,探究:写出和的度数之间的关系,并说明理由.
试卷第1页,共3页
答案
1.C
2.B
3.D
4.B
5.A
6.C
7.B
8.D
9.B
10.B
11.北偏西25°
12.125°
13.②③⑤
14.5或23
15.解:(1)∠1和∠2是内错角,∠1和∠3是同旁内角,∠1和∠4是同位角;
(2)∠1和∠2相等,∠1和∠3互补.
理由如下:
∵∠1=∠4,
∴DE∥BC,
∴∠1=∠2,∠1+∠3=180°
16.证明:∵OE平分∠AOB,OF平分∠BOC,(已知)
∴∠1=∠AOB,∠2=∠BOC.(角平分线的定义)
又∵∠AOB+∠BOC=180°,(已知)
∴∠1+∠2=(∠AOB+∠BOC)=90°.(等式性质)
∴OE⊥OF.(垂直的定义)
17.(1)解:根据题意得:的对顶角为;
的补角是,
故答案为:,;
(2)解:∵,,
∴,
∵,
∴,
∵,
∴.
18.解:设,则,
∵平分,
∴,
∵,
∴,
∴,
∵,
∴,
∵平分,
∴,
∵,
∴.
19.(1)解:∵,,
∴,,
又平分,
∴,
∴;
(2)解:∵,,
∴,,
又平分,
∴,
∴;
(3),理由如下:
∵点在上,
∴,
∵平分,
∴,
∵,
∴,
即:.
答案第1页,共2页
