青岛版八年级下册数学 6.1 平行四边形及其性质 课件(共18张PPT)
文档属性
| 名称 | 青岛版八年级下册数学 6.1 平行四边形及其性质 课件(共18张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-22 08:16:54 | ||
图片预览






文档简介
(共18张PPT)
第6章 平行四边形
6.1 平行四边形及其性质(1)
Contents
目录
01
02
03
04
旧知回顾
学习目标
新知探究
随堂练习
05
课堂小结
1、理解平行四边形的概念定义;
2、探索并掌握平行四边形对边相等、对角相等等性质,并根据性质进行简单的推理.
1、四边形的内角和为_____, 外角和为_____.
3、如何测得点a到直线b的距离?
2、已知:a∥b,c∥d,则
⑴ ∠1=∠2( )
∠2=∠3( )
⑵ ∠1+∠4=___ ( )
∠3+∠4=___ ( )
∴∠1=∠3 ( )
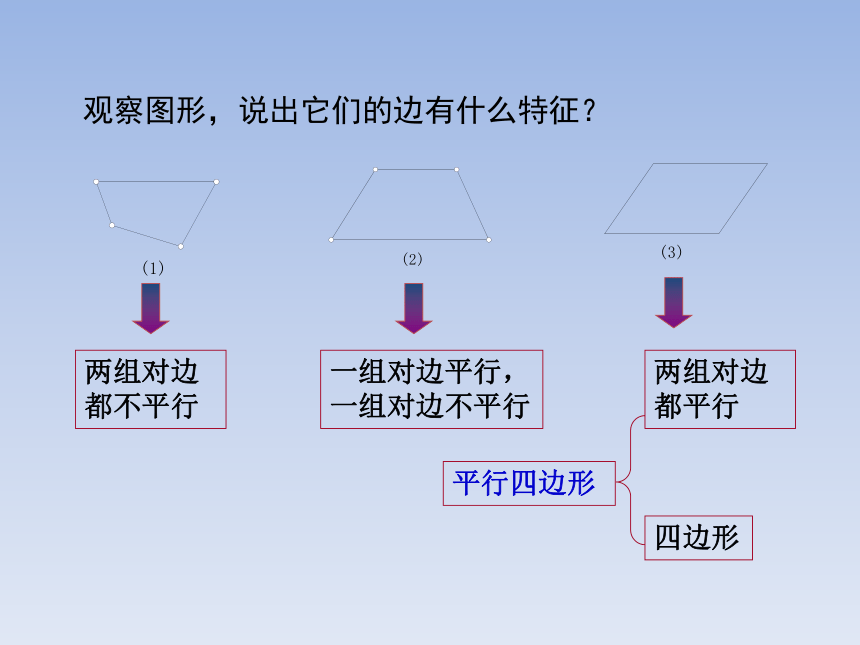
两组对边都不平行
一组对边平行,一组对边不平行
两组对边都平行
四边形
平行四边形
观察图形,说出它们的边有什么特征?
你能举出生活中常见的一些含有平行四边形的实例吗?
两组对边分别平行的四边形叫做平行四边形.
读作:平行四边形ABCD
A
D
B
C
记作: ABCD
平行四边形
几何语言:
∵四边形ABCD是平行四边形
∴四边形ABCD是平行四边形
AB∥CD,
AD∥BC
∴
AB∥CD,
AD∥BC
∵
A
D
B
C
平行四边形
对边分别平行的四边形
对平行四边形的理解
A
B
C
D
平行四边形相关概念
平行四边形相对的边称为对边, 相对的角称为对角.
对边:AB与CD; BC与DA.
对角: ∠ABC与∠CDA;
∠BAD与∠DCB.
如图,EF∥BC∥AD, GH∥AB∥CD, EF与GH相交于点O,则图中共有___个平行四边形.
A
O
H
F
E
D
C
B
G
9
用两个全等的三角形纸片可以拼出几种形状不同的平行四边形?
从拼图可以得到什么启示?
小结:
平行四边形可以是由两个全等的三角形组成,因此在解决平行四边形的问题时,通常可以连接对角线转化为两个全等的三角形进行解题.
已知: ABCD
求证:AB=CD,BC=DA;
∠B=∠D,∠A=∠C.
1
2
3
4
即∠BAD=∠DCB
∵四边形ABCD是平行四边形
∴AB∥CD,AD∥BC
∴∠1=∠2,∠3=∠4
∠1=∠2
AC=CA
∠3=∠4
∴ △ABC≌△CDA(ASA)
∴AB=CD,BC=DA,
∠B=∠D
又∵∠1=∠2,∠4=∠3
∴∠1+∠4=∠2+∠3
在△ABC和△CDA中
证明:连接AC
平行四边形的性质定理
几何语言:
A
D
B
C
∵四边形ABCD是平行四边形
∴AB=CD,AD=BC
性质定理1:平行四边形的对边相等.
性质定理2:平行四边形的对角相等.
∵四边形ABCD是平行四边形
∴∠A=∠C,∠B=∠D
几何语言:
求证:(1)夹在两平行直线间的平行线段相等.
(2)如果两条直线平行,那么一条直线上
各点到另一条直线的距离相等.
(1)已知:如图, , A,D是直线 上的任意两点,过点 A,D 作 , 分别交 于点B, C.
求证:AB=CD
证明:
(平行四边形定义)
(平行四边形的性质定理1)
例1
已知:如图, ,A,D是直线 上的任意两点,AB ,
垂足是B, DC ,垂足是C.
求证:AB=CD
证明:
(2)求证:如果两条直线平行,那么一条直线上各点到另一条直线的距离相等.
1.如图,在
若∠A=130°,则∠B=______ 、∠C=______ 、∠D=______
ABCD中,
A:基础知识:
B:变式训练:
(1)若∠A+ ∠C= 200°,则∠A=______ 、∠B=______
(2)若∠A:∠B= 5:4,则∠C=______ 、∠D=______
C
D
A
B
50°
130°
50°
100°
80°
100°
80°
C:拓展延伸:
如图,在
ABCD中,
1、∠A:∠B: ∠C :∠D的度数可能是( )
A、1:2:3:4 B、3:2:3:2
C、2:3:3:2 D、2:2:3:3
2、连接AC, 若∠D=80°, ∠DAC=40°则, ∠B=_____,
∠BAC=______.
B
80°
60°
习题P8,第1、2题.
作 业
本节课主要学习了哪些知识
1、本节课研究了什么图形的性质?
2、什么是平行四边形?
3、平行四边形有哪些性质?
性质定理1:平行四边形的对边相等.
性质定理2:平行四边形的对角相等.
第6章 平行四边形
6.1 平行四边形及其性质(1)
Contents
目录
01
02
03
04
旧知回顾
学习目标
新知探究
随堂练习
05
课堂小结
1、理解平行四边形的概念定义;
2、探索并掌握平行四边形对边相等、对角相等等性质,并根据性质进行简单的推理.
1、四边形的内角和为_____, 外角和为_____.
3、如何测得点a到直线b的距离?
2、已知:a∥b,c∥d,则
⑴ ∠1=∠2( )
∠2=∠3( )
⑵ ∠1+∠4=___ ( )
∠3+∠4=___ ( )
∴∠1=∠3 ( )
两组对边都不平行
一组对边平行,一组对边不平行
两组对边都平行
四边形
平行四边形
观察图形,说出它们的边有什么特征?
你能举出生活中常见的一些含有平行四边形的实例吗?
两组对边分别平行的四边形叫做平行四边形.
读作:平行四边形ABCD
A
D
B
C
记作: ABCD
平行四边形
几何语言:
∵四边形ABCD是平行四边形
∴四边形ABCD是平行四边形
AB∥CD,
AD∥BC
∴
AB∥CD,
AD∥BC
∵
A
D
B
C
平行四边形
对边分别平行的四边形
对平行四边形的理解
A
B
C
D
平行四边形相关概念
平行四边形相对的边称为对边, 相对的角称为对角.
对边:AB与CD; BC与DA.
对角: ∠ABC与∠CDA;
∠BAD与∠DCB.
如图,EF∥BC∥AD, GH∥AB∥CD, EF与GH相交于点O,则图中共有___个平行四边形.
A
O
H
F
E
D
C
B
G
9
用两个全等的三角形纸片可以拼出几种形状不同的平行四边形?
从拼图可以得到什么启示?
小结:
平行四边形可以是由两个全等的三角形组成,因此在解决平行四边形的问题时,通常可以连接对角线转化为两个全等的三角形进行解题.
已知: ABCD
求证:AB=CD,BC=DA;
∠B=∠D,∠A=∠C.
1
2
3
4
即∠BAD=∠DCB
∵四边形ABCD是平行四边形
∴AB∥CD,AD∥BC
∴∠1=∠2,∠3=∠4
∠1=∠2
AC=CA
∠3=∠4
∴ △ABC≌△CDA(ASA)
∴AB=CD,BC=DA,
∠B=∠D
又∵∠1=∠2,∠4=∠3
∴∠1+∠4=∠2+∠3
在△ABC和△CDA中
证明:连接AC
平行四边形的性质定理
几何语言:
A
D
B
C
∵四边形ABCD是平行四边形
∴AB=CD,AD=BC
性质定理1:平行四边形的对边相等.
性质定理2:平行四边形的对角相等.
∵四边形ABCD是平行四边形
∴∠A=∠C,∠B=∠D
几何语言:
求证:(1)夹在两平行直线间的平行线段相等.
(2)如果两条直线平行,那么一条直线上
各点到另一条直线的距离相等.
(1)已知:如图, , A,D是直线 上的任意两点,过点 A,D 作 , 分别交 于点B, C.
求证:AB=CD
证明:
(平行四边形定义)
(平行四边形的性质定理1)
例1
已知:如图, ,A,D是直线 上的任意两点,AB ,
垂足是B, DC ,垂足是C.
求证:AB=CD
证明:
(2)求证:如果两条直线平行,那么一条直线上各点到另一条直线的距离相等.
1.如图,在
若∠A=130°,则∠B=______ 、∠C=______ 、∠D=______
ABCD中,
A:基础知识:
B:变式训练:
(1)若∠A+ ∠C= 200°,则∠A=______ 、∠B=______
(2)若∠A:∠B= 5:4,则∠C=______ 、∠D=______
C
D
A
B
50°
130°
50°
100°
80°
100°
80°
C:拓展延伸:
如图,在
ABCD中,
1、∠A:∠B: ∠C :∠D的度数可能是( )
A、1:2:3:4 B、3:2:3:2
C、2:3:3:2 D、2:2:3:3
2、连接AC, 若∠D=80°, ∠DAC=40°则, ∠B=_____,
∠BAC=______.
B
80°
60°
习题P8,第1、2题.
作 业
本节课主要学习了哪些知识
1、本节课研究了什么图形的性质?
2、什么是平行四边形?
3、平行四边形有哪些性质?
性质定理1:平行四边形的对边相等.
性质定理2:平行四边形的对角相等.
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
