2.2.1 利用”同位角“判定两直线平行与平行公理基础训练(含解析)
文档属性
| 名称 | 2.2.1 利用”同位角“判定两直线平行与平行公理基础训练(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 312.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-22 15:40:28 | ||
图片预览

文档简介
必刷题《2.2.1利用“同位角”判定两直线平行与平行公理》刷基础
知识点一 同位角
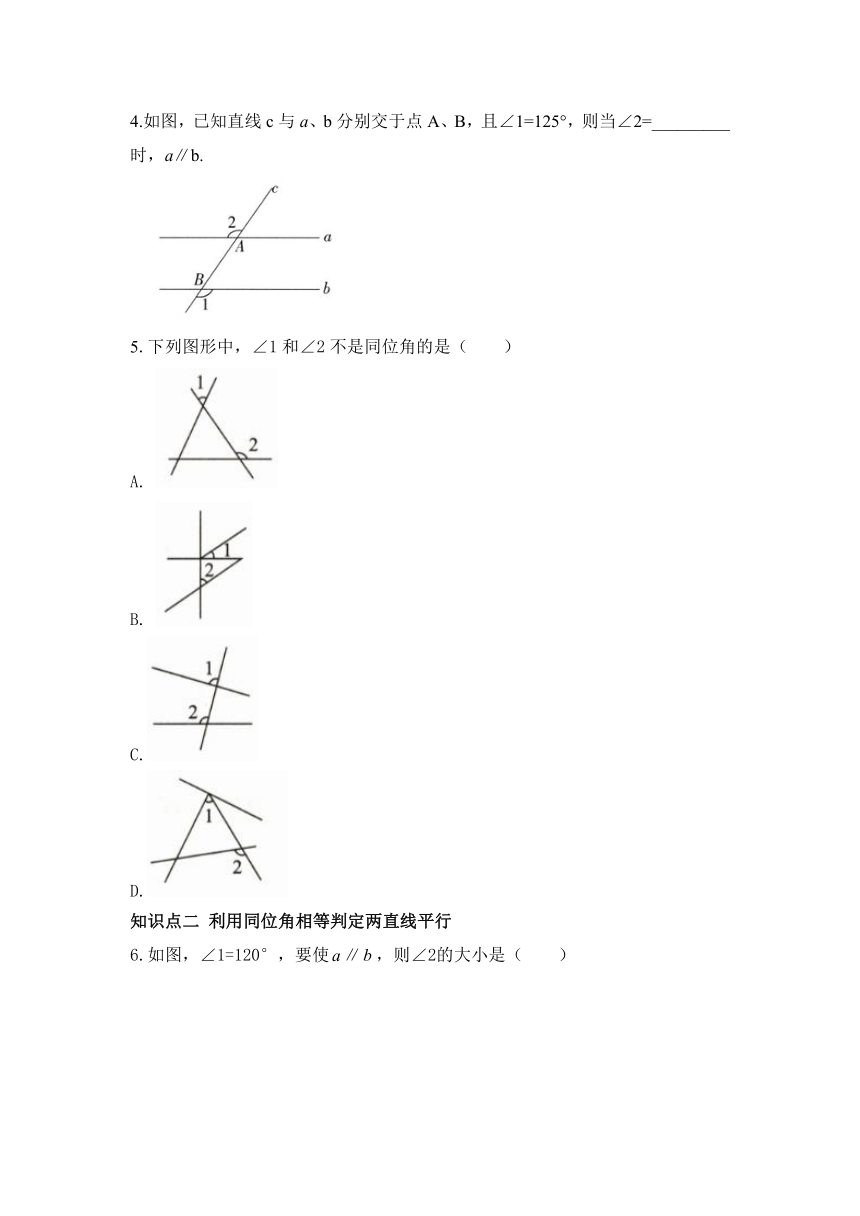
1.如图,直线被直线所截,与∠1是同位角的是( )
A.∠2
B.∠3
C.∠4
D.∠5
2.如图,将木条a,b与c钉在一起,∠1=70°,∠2=50°,要使木条a与b平行,则木条a旋转的度数至少是( )
A.10°
B.20°
C.50°
D.70°
3.如图,下列条件中,可以用“同位角相等,两直线平行”判定AB∥CD的是( )
A.∠1=∠5
B.∠B=∠5
C.∠2=∠5
D.∠5+∠B=180°
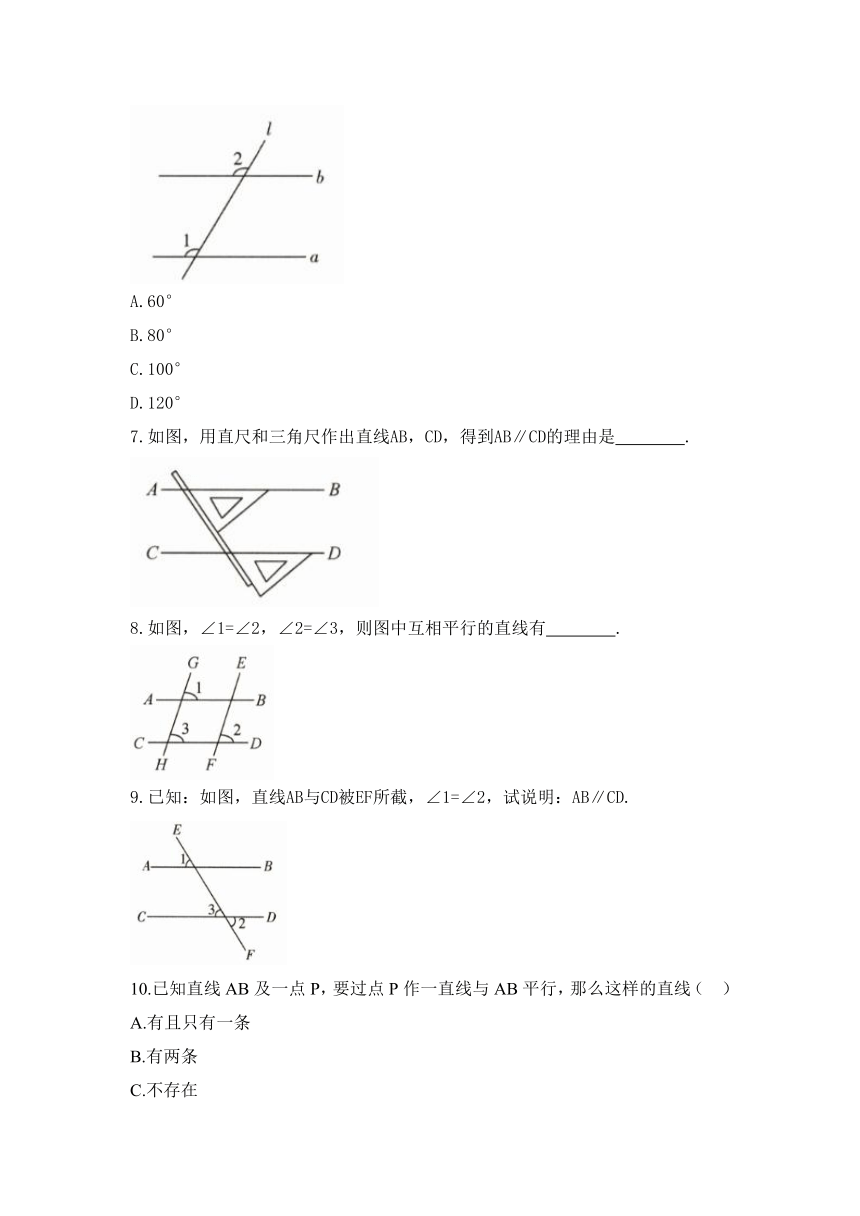
4.如图,已知直线c与a、b分别交于点A、B,且∠1=125°,则当∠2=_________时,a∥b.
5.下列图形中,∠1和∠2不是同位角的是( )
A.
B.
C.
D.
知识点二 利用同位角相等判定两直线平行
6.如图,∠1=120°,要使∥,则∠2的大小是( )
A.60°
B.80°
C.100°
D.120°
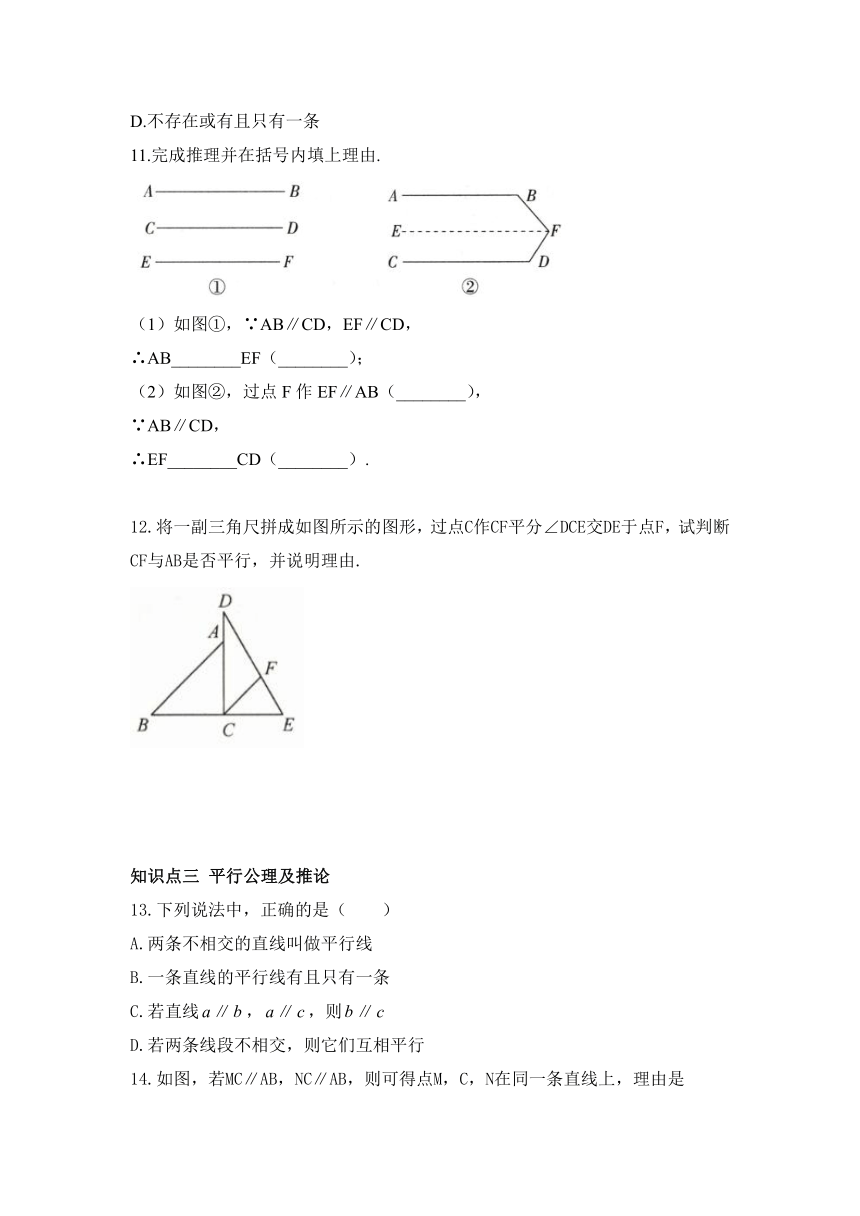
7.如图,用直尺和三角尺作出直线AB,CD,得到AB∥CD的理由是 .
8.如图,∠1=∠2,∠2=∠3,则图中互相平行的直线有 .
9.已知:如图,直线AB与CD被EF所截,∠1=∠2,试说明:AB∥CD.
10.已知直线AB及一点P,要过点P作一直线与AB平行,那么这样的直线( )
A.有且只有一条
B.有两条
C.不存在
D.不存在或有且只有一条
11.完成推理并在括号内填上理由.
(1)如图①,∵AB∥CD,EF∥CD,
∴AB________EF(________);
(2)如图②,过点F作EF∥AB(________),
∵AB∥CD,
∴EF________CD(________).
12.将一副三角尺拼成如图所示的图形,过点C作CF平分∠DCE交DE于点F,试判断CF与AB是否平行,并说明理由.
知识点三 平行公理及推论
13.下列说法中,正确的是( )
A.两条不相交的直线叫做平行线
B.一条直线的平行线有且只有一条
C.若直线∥,∥,则∥
D.若两条线段不相交,则它们互相平行
14.如图,若MC∥AB,NC∥AB,则可得点M,C,N在同一条直线上,理由是
.
15.如图,将一张长方形的硬纸片ABCD对折后打开,折痕为EF,把长方形ABEF平摊在桌面上,另一面CDFE无论怎样改变位置,总有CD∥AB,为什么?
知识点四 易错点 对平行的前提条件理解不透
16.下列语句:
①不相交的两条直线叫平行线;
②在同一平面内,两条直线的位置关系只有两种:相交和平行;
③如果线段AB和线段CD不相交,那么直线AB和直线CD平行;
④如果两条直线都和第三条直线平行,那么这两条直线平行;
⑤过一点有且只有一条直线与已知直线平行.
正确的个数是( )
A.1
B.2
C.3
D.4
参考答案
1.答案:B
解析:因为直线被直线所截,∠1与∠3在直线的同侧,在直线的同旁,所以∠3与∠1是同位角,故选B.
2.答案:B
解析:要使a∥b,需∠1=∠2=50°,70°-50°=20°,故选B.
3.答案:B
解析:∠5和∠B是直线AB和直线CD被直线BE所截得的同位角.故选B.
4.答案:125°
解析:如图,∠1=∠3=125°,根据同位角相等,两直线平行可知当∠2=∠3=125°时,a∥b.
5.答案:B
解析:“三线八角”是由三条直线构成的,因为选项B中∠1和∠2是由四条直线构成的,所以∠1和∠2不是同位角.故选B.
6.答案:D
解析:如果∠2=∠1=120°,那么∥.所以要使∥,则∠2的大小是120°.故选D.
7.答案:同位角相等,两直线平行
解析:由图可知,作出的是一对相等的同位角.
8.答案:EF∥GH,AB∥CD
解析:因为∠1=∠2,∠2=∠3,所以∠1=∠3,根据“同位角相等,两直线平行”可判定AB∥CD,EF∥GH.
9.答案:因为∠2=∠3(对顶角相等),又因为∠1=∠2(已知),所以∠1=∠3,所以AB∥CD(同位角相等,两直线平行).
解析:
10.答案:D
解析:当点P在直线AB上时,这样的直线不存在;当点P在直线AB外时,这样的直线有且只有一条.
11.答案:见解析
解析:(1)∵AB∥CD,EF∥CD,
∴AB∥EF(平行于同一条直线的两条直线互相平行).
(2)过点F作EF∥AB(过直线外一点可作一条直线与已知直线平行),
∵AB∥CD,
∴EF∥CD(平行于同一条直线的两条直线互相平行).
12.答案:CF∥AB.理由如下:因为图中是一副三角尺,所以∠DCE=90°,∠B=45°.因为CF平分∠DCE,所以∠ECF=∠DCE=45°.所以∠B=∠ECF.所以CF∥AB(同位角相等,两直线平行).
解析:
13.答案:C
解析:在同一平面内,两条不相交的直线才是平行线,选项A错误;一条直线的平行线有无数条,选项B错误;若直线∥,∥,根据“平行于同一条直线的两条直线互相平行”,知∥,选项C正确;判断两条线段是否平行,是看它们所在的直线是否平行,选项D错误.故选C.
14.答案:过直线外一点有且只有一条直线与这条直线平行
解析:因为MC∥AB,NC∥AB,由“过直线外一点有且只有一条直线与这条直线平行”可知M,C,N在同一条直线上.
15.答案:因为AB∥EF,CD∥EF,所以AB∥CD(平行于同一条直线的两条直线互相平行).
解析:
16.答案:B
解析:①不相交的两条直线叫平行线,前提必须是在同一平面内,故错误;②在同一平面内,两条直线的位置关系只有两种:相交和平行,正确;③如果线段AB和线段CD不相交,那么直线AB和直线CD不一定平行,错误;④如果两条直线都和第三条直线平行,那么这两条直线平行,正确;⑤过直线外一点有且只有一条直线与已知直线平行,故错误.故选B.
易错警示 判断两条直线的位置关系,必须强调在同一平面内;如果不强调有可能两条直线是异面(高中会学).
知识点一 同位角
1.如图,直线被直线所截,与∠1是同位角的是( )
A.∠2
B.∠3
C.∠4
D.∠5
2.如图,将木条a,b与c钉在一起,∠1=70°,∠2=50°,要使木条a与b平行,则木条a旋转的度数至少是( )
A.10°
B.20°
C.50°
D.70°
3.如图,下列条件中,可以用“同位角相等,两直线平行”判定AB∥CD的是( )
A.∠1=∠5
B.∠B=∠5
C.∠2=∠5
D.∠5+∠B=180°
4.如图,已知直线c与a、b分别交于点A、B,且∠1=125°,则当∠2=_________时,a∥b.
5.下列图形中,∠1和∠2不是同位角的是( )
A.
B.
C.
D.
知识点二 利用同位角相等判定两直线平行
6.如图,∠1=120°,要使∥,则∠2的大小是( )
A.60°
B.80°
C.100°
D.120°
7.如图,用直尺和三角尺作出直线AB,CD,得到AB∥CD的理由是 .
8.如图,∠1=∠2,∠2=∠3,则图中互相平行的直线有 .
9.已知:如图,直线AB与CD被EF所截,∠1=∠2,试说明:AB∥CD.
10.已知直线AB及一点P,要过点P作一直线与AB平行,那么这样的直线( )
A.有且只有一条
B.有两条
C.不存在
D.不存在或有且只有一条
11.完成推理并在括号内填上理由.
(1)如图①,∵AB∥CD,EF∥CD,
∴AB________EF(________);
(2)如图②,过点F作EF∥AB(________),
∵AB∥CD,
∴EF________CD(________).
12.将一副三角尺拼成如图所示的图形,过点C作CF平分∠DCE交DE于点F,试判断CF与AB是否平行,并说明理由.
知识点三 平行公理及推论
13.下列说法中,正确的是( )
A.两条不相交的直线叫做平行线
B.一条直线的平行线有且只有一条
C.若直线∥,∥,则∥
D.若两条线段不相交,则它们互相平行
14.如图,若MC∥AB,NC∥AB,则可得点M,C,N在同一条直线上,理由是
.
15.如图,将一张长方形的硬纸片ABCD对折后打开,折痕为EF,把长方形ABEF平摊在桌面上,另一面CDFE无论怎样改变位置,总有CD∥AB,为什么?
知识点四 易错点 对平行的前提条件理解不透
16.下列语句:
①不相交的两条直线叫平行线;
②在同一平面内,两条直线的位置关系只有两种:相交和平行;
③如果线段AB和线段CD不相交,那么直线AB和直线CD平行;
④如果两条直线都和第三条直线平行,那么这两条直线平行;
⑤过一点有且只有一条直线与已知直线平行.
正确的个数是( )
A.1
B.2
C.3
D.4
参考答案
1.答案:B
解析:因为直线被直线所截,∠1与∠3在直线的同侧,在直线的同旁,所以∠3与∠1是同位角,故选B.
2.答案:B
解析:要使a∥b,需∠1=∠2=50°,70°-50°=20°,故选B.
3.答案:B
解析:∠5和∠B是直线AB和直线CD被直线BE所截得的同位角.故选B.
4.答案:125°
解析:如图,∠1=∠3=125°,根据同位角相等,两直线平行可知当∠2=∠3=125°时,a∥b.
5.答案:B
解析:“三线八角”是由三条直线构成的,因为选项B中∠1和∠2是由四条直线构成的,所以∠1和∠2不是同位角.故选B.
6.答案:D
解析:如果∠2=∠1=120°,那么∥.所以要使∥,则∠2的大小是120°.故选D.
7.答案:同位角相等,两直线平行
解析:由图可知,作出的是一对相等的同位角.
8.答案:EF∥GH,AB∥CD
解析:因为∠1=∠2,∠2=∠3,所以∠1=∠3,根据“同位角相等,两直线平行”可判定AB∥CD,EF∥GH.
9.答案:因为∠2=∠3(对顶角相等),又因为∠1=∠2(已知),所以∠1=∠3,所以AB∥CD(同位角相等,两直线平行).
解析:
10.答案:D
解析:当点P在直线AB上时,这样的直线不存在;当点P在直线AB外时,这样的直线有且只有一条.
11.答案:见解析
解析:(1)∵AB∥CD,EF∥CD,
∴AB∥EF(平行于同一条直线的两条直线互相平行).
(2)过点F作EF∥AB(过直线外一点可作一条直线与已知直线平行),
∵AB∥CD,
∴EF∥CD(平行于同一条直线的两条直线互相平行).
12.答案:CF∥AB.理由如下:因为图中是一副三角尺,所以∠DCE=90°,∠B=45°.因为CF平分∠DCE,所以∠ECF=∠DCE=45°.所以∠B=∠ECF.所以CF∥AB(同位角相等,两直线平行).
解析:
13.答案:C
解析:在同一平面内,两条不相交的直线才是平行线,选项A错误;一条直线的平行线有无数条,选项B错误;若直线∥,∥,根据“平行于同一条直线的两条直线互相平行”,知∥,选项C正确;判断两条线段是否平行,是看它们所在的直线是否平行,选项D错误.故选C.
14.答案:过直线外一点有且只有一条直线与这条直线平行
解析:因为MC∥AB,NC∥AB,由“过直线外一点有且只有一条直线与这条直线平行”可知M,C,N在同一条直线上.
15.答案:因为AB∥EF,CD∥EF,所以AB∥CD(平行于同一条直线的两条直线互相平行).
解析:
16.答案:B
解析:①不相交的两条直线叫平行线,前提必须是在同一平面内,故错误;②在同一平面内,两条直线的位置关系只有两种:相交和平行,正确;③如果线段AB和线段CD不相交,那么直线AB和直线CD不一定平行,错误;④如果两条直线都和第三条直线平行,那么这两条直线平行,正确;⑤过直线外一点有且只有一条直线与已知直线平行,故错误.故选B.
易错警示 判断两条直线的位置关系,必须强调在同一平面内;如果不强调有可能两条直线是异面(高中会学).
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
