2.2.2 利用“内错角、同旁内角”判定两直线平行基础训练(含解析)
文档属性
| 名称 | 2.2.2 利用“内错角、同旁内角”判定两直线平行基础训练(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 412.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-22 17:07:13 | ||
图片预览


文档简介
必刷题《2.2.2利用“内错角、同旁内角”判定两直线平行》刷基础
知识点一 内错角
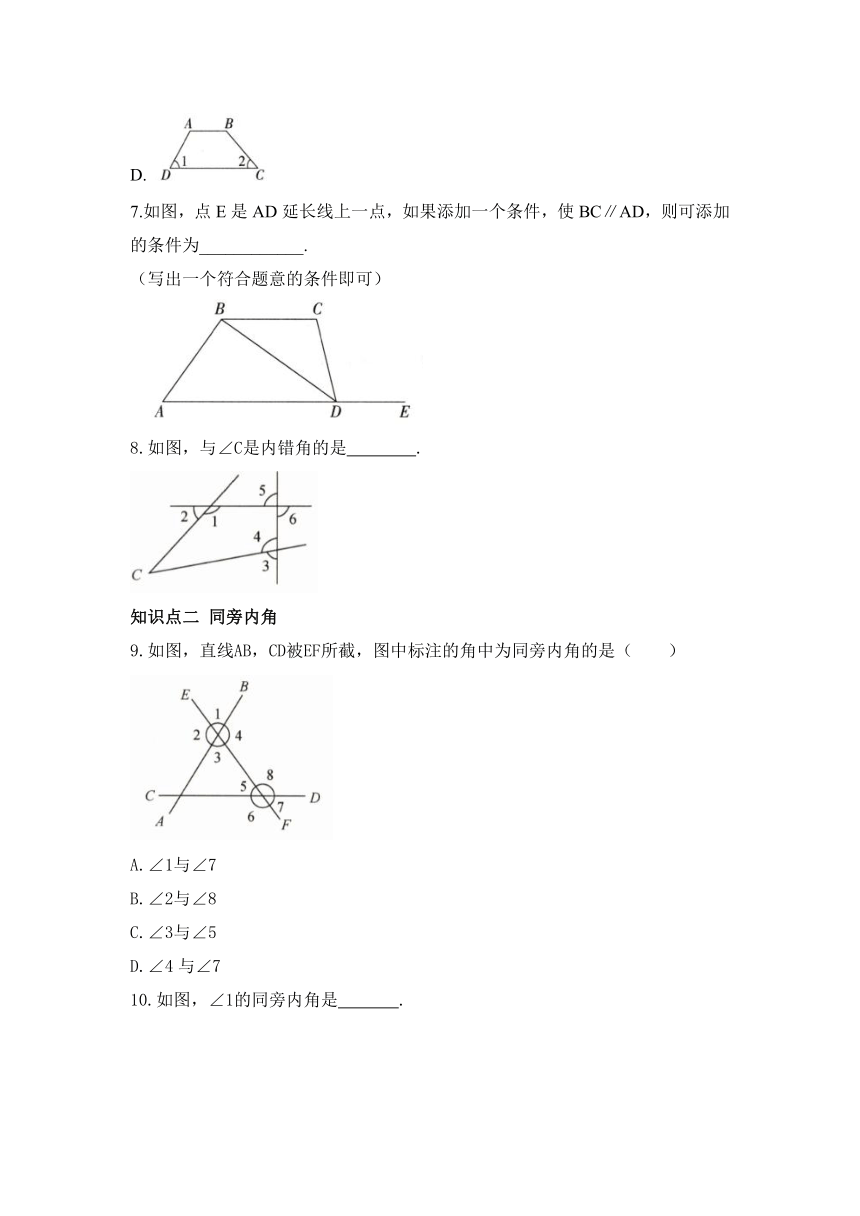
1.试在图中找出∠1的内错角.
2.请指出图中∠A的同旁内角.
3.下列图形中,∠1和∠2是内错角的是( )
A.
B.
C.
D.
4.如图所示,两只手的食指和拇指在同一平面内,它们构成的一对角可以看成( )
A.内错角
B.同位角
C.同旁内角
D.对顶角
5.如图,不能判定直线a∥b的条件是( )
A.∠1=∠3
B.∠1=∠4
C.∠2+∠4=180°
D.∠1=∠5
6.下列图形中,由∠1=∠2能得到AB∥CD的是( )
A.
B.
C.
D.
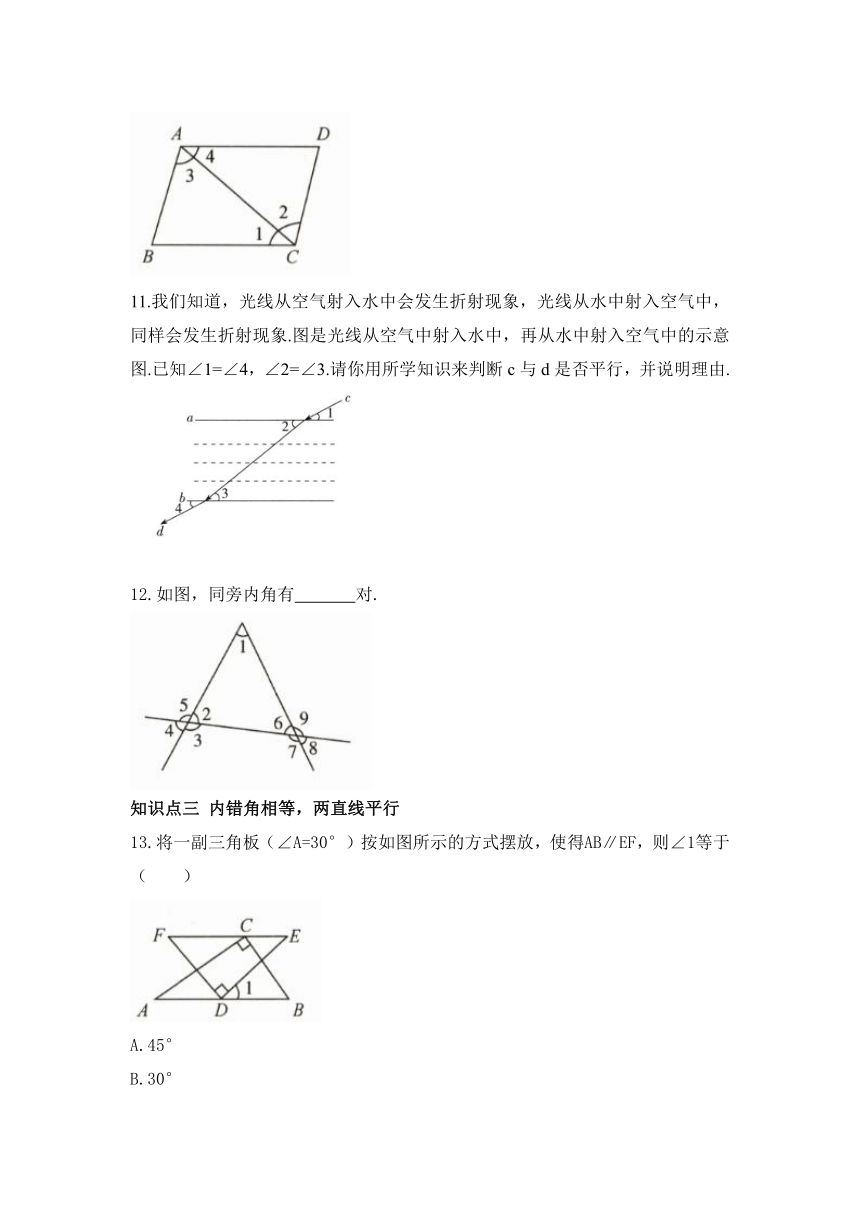
7.如图,点E是AD延长线上一点,如果添加一个条件,使BC∥AD,则可添加的条件为____________.
(写出一个符合题意的条件即可)
8.如图,与∠C是内错角的是 .
知识点二 同旁内角
9.如图,直线AB,CD被EF所截,图中标注的角中为同旁内角的是( )
A.∠1与∠7
B.∠2与∠8
C.∠3与∠5
D.∠4与∠7
10.如图,∠1的同旁内角是 .
11.我们知道,光线从空气射入水中会发生折射现象,光线从水中射入空气中,同样会发生折射现象.图是光线从空气中射入水中,再从水中射入空气中的示意图.已知∠1=∠4,∠2=∠3.请你用所学知识来判断c与d是否平行,并说明理由.
12.如图,同旁内角有 对.
知识点三 内错角相等,两直线平行
13.将一副三角板(∠A=30°)按如图所示的方式摆放,使得AB∥EF,则∠1等于( )
A.45°
B.30°
C.65°
D.75°
14.如图,已知∠A=∠F,∠C=∠E,试说明:BE∥CD.
知识点四 同旁内角互补,两直线平行
15.如图,是一个由4条线段构成的“鱼”形图案,已知:∠1=50°,∠2=50°,∠3=130°.找出图中所有的平行线,并说明理由.
参考答案
1.答案:见解析
解析:将题图分解为如图①②所示的两个图形.
所以∠1的内错角有两个,分别为∠CGB,∠FGB.
2.答案:见解析
解析:将题图分解为如图①②所示的两个图形.
所以∠A的同旁内角有三个,分别为∠ACD,∠ACB,∠B.
3.答案:B
解析:若两个角是内错角,则这两个角必须位于两条被截直线之间(内),且位于截线两侧,符合这个要求的是选项B的图,故选B.
4.答案:A
解析:两只手的食指和拇指在同一平面内,它们构成的一对角可看成是内错角.故选A.
5.答案:D
解析:A项,∠1=∠3时,直线a∥b,故此选项不符合题意;B项,∠1=∠4时,直线a∥b,故此选项不符合题意;C项,∠2+∠4=180°时,直线a∥b,故此选项不符合题意;D项,∠1=∠5时,无法得到直线a∥b,故此选项符合题意.故选D.
6.答案:B
解析:根据内错角相等,两直线平行,可知B选项正确,故选B.
7.答案:∠A+∠ABC=180°(答案不唯一)
解析:若∠A+∠ABC=180°,则BC∥AD;
若∠C+∠ADC=180°,则BC∥AD;
若∠CBD=∠ADB,则BC∥AD;
若∠C=∠CDE,则BC∥AD.
8.答案:∠2,∠3
解析:如题图所示,与∠C是内错角的是∠2,∠3.故答案是∠2,∠3.
9.答案:C
解析:∠1与∠7不是直线AB,CD被EF所截而成的同旁内角,故A选项错误;∠2与∠8不是直线AB,CD被EF所截而成的同旁内角,故B选项错误;∠3与∠5是直线AB,CD被EF所截而成的同旁内角,故C选项正确;∠4与∠7不是直线AB,CD被EF所截而成的同旁内角,故D选项错误.故选C.
10.答案:∠3,∠B
解析:∠1与∠3,∠1和∠B是同旁内角.
11.答案:见解析
解析:c∥d理由如下:如图,
因为∠2+∠5=∠3+∠6,∠2=∠3,所以∠5=∠6,
因为∠1=∠4,所以∠1+∠5=∠4+∠6(等式的性质),
所以c∥d(内错角相等,两直线平行).
12.答案:4
解析:∠1和∠2,∠1和∠6,∠2和∠6,∠3和∠7是同旁内角,共4对.故答案为4.
13.答案:A
解析:因为△DEF中,∠E=45°,所以当∠1=45°时,∠1=∠E,所以EF∥AB.故选A.
14.答案:如图,设AF与BE,CD分别交于点G,H.因为∠A=∠F,∠C=∠E,∠A+∠C+∠AHC=180°,∠F+∠E+∠FGE=180°,所以∠AHC=∠FGE,所以BE∥CD(内错角相等,两直线平行).
解析:
15.答案:BF∥CE,BC∥EF.
理由如下:因为∠1=50°,∠2=50°,所以∠1=∠2,所以BF∥CE.因为∠2=50°,∠3=130°,所以∠2+∠3=180°,所以BC∥EF.
解析:
知识点一 内错角
1.试在图中找出∠1的内错角.
2.请指出图中∠A的同旁内角.
3.下列图形中,∠1和∠2是内错角的是( )
A.
B.
C.
D.
4.如图所示,两只手的食指和拇指在同一平面内,它们构成的一对角可以看成( )
A.内错角
B.同位角
C.同旁内角
D.对顶角
5.如图,不能判定直线a∥b的条件是( )
A.∠1=∠3
B.∠1=∠4
C.∠2+∠4=180°
D.∠1=∠5
6.下列图形中,由∠1=∠2能得到AB∥CD的是( )
A.
B.
C.
D.
7.如图,点E是AD延长线上一点,如果添加一个条件,使BC∥AD,则可添加的条件为____________.
(写出一个符合题意的条件即可)
8.如图,与∠C是内错角的是 .
知识点二 同旁内角
9.如图,直线AB,CD被EF所截,图中标注的角中为同旁内角的是( )
A.∠1与∠7
B.∠2与∠8
C.∠3与∠5
D.∠4与∠7
10.如图,∠1的同旁内角是 .
11.我们知道,光线从空气射入水中会发生折射现象,光线从水中射入空气中,同样会发生折射现象.图是光线从空气中射入水中,再从水中射入空气中的示意图.已知∠1=∠4,∠2=∠3.请你用所学知识来判断c与d是否平行,并说明理由.
12.如图,同旁内角有 对.
知识点三 内错角相等,两直线平行
13.将一副三角板(∠A=30°)按如图所示的方式摆放,使得AB∥EF,则∠1等于( )
A.45°
B.30°
C.65°
D.75°
14.如图,已知∠A=∠F,∠C=∠E,试说明:BE∥CD.
知识点四 同旁内角互补,两直线平行
15.如图,是一个由4条线段构成的“鱼”形图案,已知:∠1=50°,∠2=50°,∠3=130°.找出图中所有的平行线,并说明理由.
参考答案
1.答案:见解析
解析:将题图分解为如图①②所示的两个图形.
所以∠1的内错角有两个,分别为∠CGB,∠FGB.
2.答案:见解析
解析:将题图分解为如图①②所示的两个图形.
所以∠A的同旁内角有三个,分别为∠ACD,∠ACB,∠B.
3.答案:B
解析:若两个角是内错角,则这两个角必须位于两条被截直线之间(内),且位于截线两侧,符合这个要求的是选项B的图,故选B.
4.答案:A
解析:两只手的食指和拇指在同一平面内,它们构成的一对角可看成是内错角.故选A.
5.答案:D
解析:A项,∠1=∠3时,直线a∥b,故此选项不符合题意;B项,∠1=∠4时,直线a∥b,故此选项不符合题意;C项,∠2+∠4=180°时,直线a∥b,故此选项不符合题意;D项,∠1=∠5时,无法得到直线a∥b,故此选项符合题意.故选D.
6.答案:B
解析:根据内错角相等,两直线平行,可知B选项正确,故选B.
7.答案:∠A+∠ABC=180°(答案不唯一)
解析:若∠A+∠ABC=180°,则BC∥AD;
若∠C+∠ADC=180°,则BC∥AD;
若∠CBD=∠ADB,则BC∥AD;
若∠C=∠CDE,则BC∥AD.
8.答案:∠2,∠3
解析:如题图所示,与∠C是内错角的是∠2,∠3.故答案是∠2,∠3.
9.答案:C
解析:∠1与∠7不是直线AB,CD被EF所截而成的同旁内角,故A选项错误;∠2与∠8不是直线AB,CD被EF所截而成的同旁内角,故B选项错误;∠3与∠5是直线AB,CD被EF所截而成的同旁内角,故C选项正确;∠4与∠7不是直线AB,CD被EF所截而成的同旁内角,故D选项错误.故选C.
10.答案:∠3,∠B
解析:∠1与∠3,∠1和∠B是同旁内角.
11.答案:见解析
解析:c∥d理由如下:如图,
因为∠2+∠5=∠3+∠6,∠2=∠3,所以∠5=∠6,
因为∠1=∠4,所以∠1+∠5=∠4+∠6(等式的性质),
所以c∥d(内错角相等,两直线平行).
12.答案:4
解析:∠1和∠2,∠1和∠6,∠2和∠6,∠3和∠7是同旁内角,共4对.故答案为4.
13.答案:A
解析:因为△DEF中,∠E=45°,所以当∠1=45°时,∠1=∠E,所以EF∥AB.故选A.
14.答案:如图,设AF与BE,CD分别交于点G,H.因为∠A=∠F,∠C=∠E,∠A+∠C+∠AHC=180°,∠F+∠E+∠FGE=180°,所以∠AHC=∠FGE,所以BE∥CD(内错角相等,两直线平行).
解析:
15.答案:BF∥CE,BC∥EF.
理由如下:因为∠1=50°,∠2=50°,所以∠1=∠2,所以BF∥CE.因为∠2=50°,∠3=130°,所以∠2+∠3=180°,所以BC∥EF.
解析:
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
