北师大版七年级数学下册《平行线性质与判定的综合》基础训练(含答案)
文档属性
| 名称 | 北师大版七年级数学下册《平行线性质与判定的综合》基础训练(含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 450.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-22 00:00:00 | ||
图片预览

文档简介
《平行线性质与判定的综合》基础训练
知识点1 综合运用平行线的性质与判定进行计算或说理
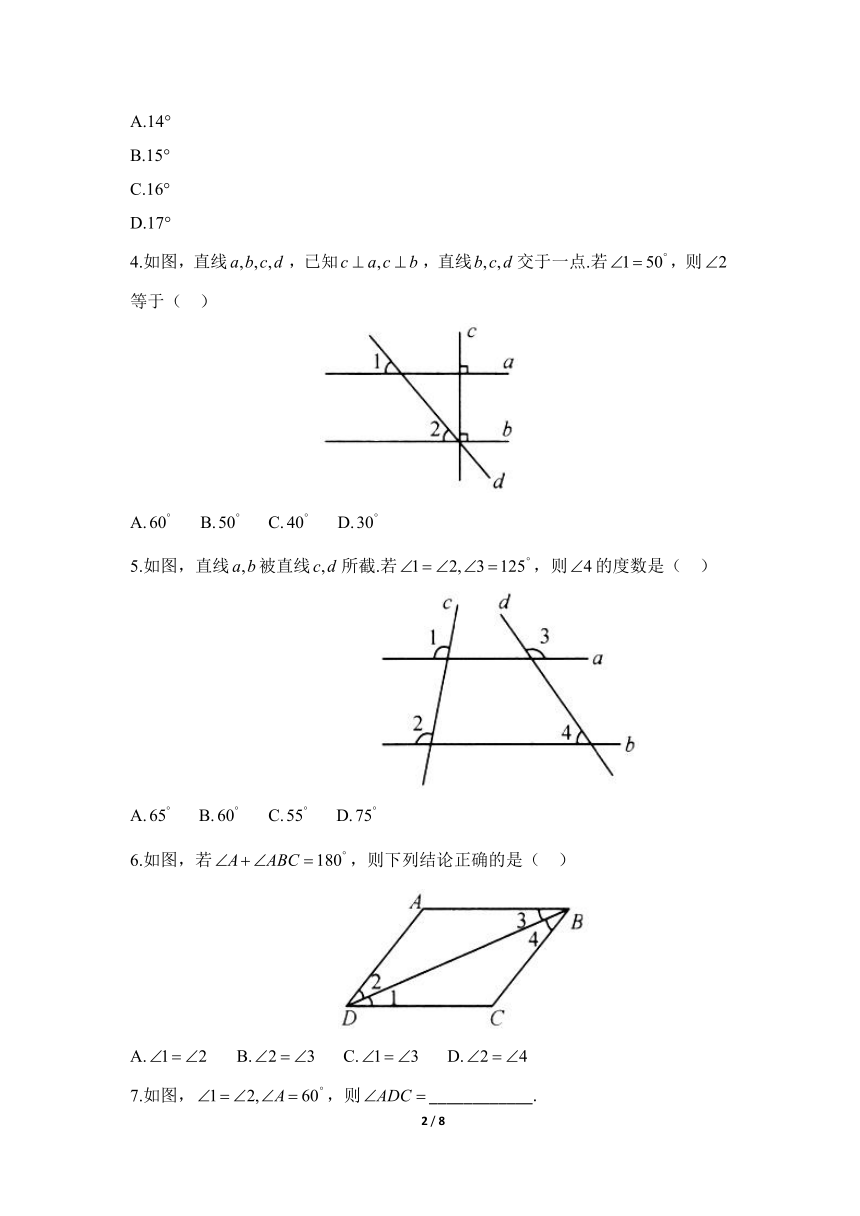
1.如图,已知a∥b,∠1=58°,则∠2的大小是( )
A.122°
B.85°
C.58°
D.32°
2.如图,直线EB∥FD,直线c分别交EB、FD于点A、C,∠BAC的平分线交直线FD于点G,若∠2=50°,则∠1的度数是( )
A.50°
B.60°
C.80°
D.100°
3.如图,一块含有30°角的直角三角板的两个顶点放在直尺的对边上.如果∠2=44°,那么∠1的度数是( )
A.14°
B.15°
C.16°
D.17°
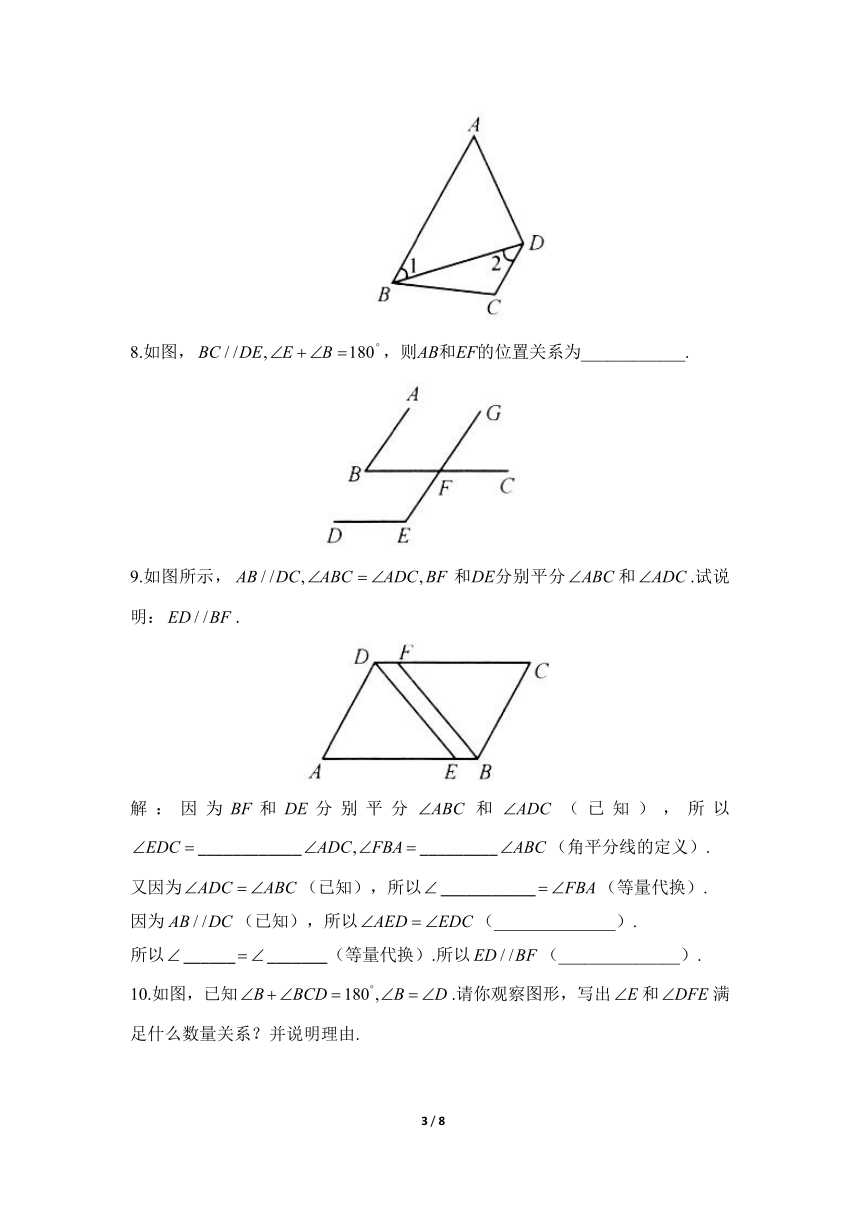
4.如图,直线,已知,直线交于一点.若,则等于( )
A. B. C. D.
5.如图,直线被直线所截.若,则的度数是( )
A. B. C. D.
6.如图,若,则下列结论正确的是( )
A. B. C. D.
7.如图,,则____________.
8.如图,,则AB和EF的位置关系为____________.
9.如图所示,和DE分别平分和.试说明:.
解:因为BF和DE分别平分和(已知),所以_____________________(角平分线的定义).
又因为(已知),所以___________(等量代换).
因为(已知),所以(______________).
所以_____________(等量代换).所以(______________).
10.如图,已知.请你观察图形,写出和满足什么数量关系?并说明理由.
知识点2 利用平行线的性质与判定解决实际问題
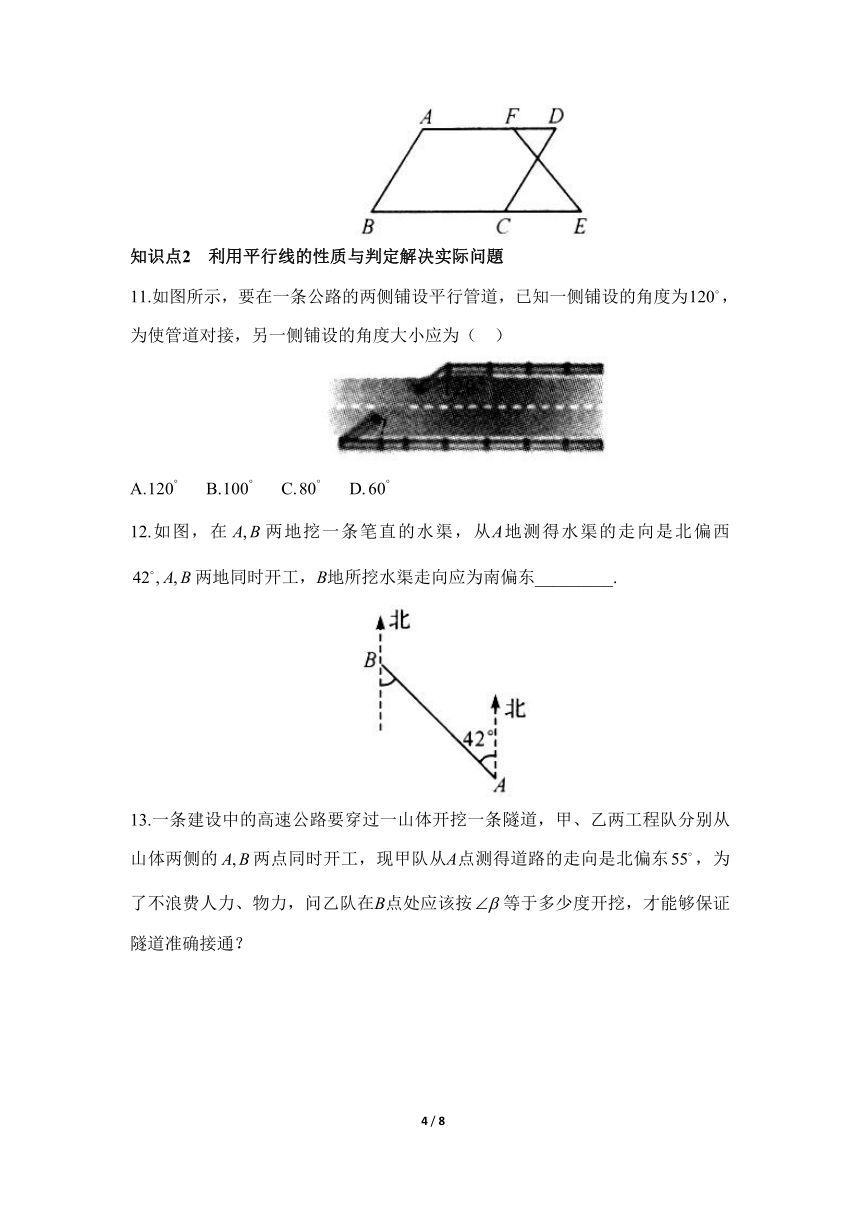
11.如图所示,要在一条公路的两侧铺设平行管道,已知一侧铺设的角度为,为使管道对接,另一侧铺设的角度大小应为( )
A. B. C. D.
12.如图,在两地挖一条笔直的水渠,从A地测得水渠的走向是北偏西两地同时开工,B地所挖水渠走向应为南偏东_________.
13.一条建设中的高速公路要穿过一山体开挖一条隧道,甲、乙两工程队分别从山体两侧的两点同时开工,现甲队从A点测得道路的走向是北偏东,为了不浪费人力、物力,问乙队在B点处应该按等于多少度开挖,才能够保证隧道准确接通?
14.如图,B处在A处的南偏西45°方向,C处在B处的北偏东80°方向.
(1)求∠ABC的度数;
(2)要使CD∥AB,D处应在C处的什么方向?
15.如图,已知CD⊥AB,GF⊥AB,∠B=∠ADE,试说明∠1=∠2.
16.如图,已知AB∥CD,∠1=∠2,∠3=∠4,求证:
(1)∠4=∠DAC;
(2)AD∥BE.
参考答案
1、B 2.C 3.D
4.答案:C
解析:∵a∥b,∴∠1=∠2,
∵∠1=58°,∴∠2=58°,故选C.
5.答案:C
解析:∵EB∥FD,∴∠BAG=∠2=50°,
∵AG平分∠BAC,∴∠GAC=∠BAG=50°,
∴∠1=180°-∠BAG-∠GAC=80°,故选C.
6.答案:C
解析:根据题意可知∠2+∠3=60°,因为∠2=44°,所以∠3=16°,再根据直尺的对边平行,可知∠1=∠3=16°.
7. 8.平行
9. 两直线平行,内错角相等 同位角相等,两直线平行
10.解:.理由如下:因为,所以.所以.所以.
11.D 12.
13.解:因为指北方向平行,且两点走向形成一条直线,即,所以和就构成了一对同旁内角.所以,即.因此,乙队在B点处应该按开挖.
14.答案:见解析
解析:(1)如图,由题意,得∠FAB=45°.
因为AF∥BE,所以∠FAB=∠ABE=45°,
因为∠EBC=80°,所以∠ABC=35°.
(2)D处在C处的南偏西45°方向.
理由如下:如图,因为CG∥BE,
所以∠GCB=∠EBC=80°.
因为∠GCD=45°,所以∠BCD=35°,
所以∠ABC=∠BCD=35°,所以CD∥AB.
15.答案:见解析
解析:证明:∵∠B=∠ADE(已知),
∴DE∥BC(同位角相等,两直线平行),
∴∠1=∠DCB(两直线平行,内错角相等).
∵CD⊥AB,GF⊥AB,∴∠BDC=90°,∠BFG=90°,
∴CD∥FG(同位角相等,两直线平行),
∴∠2=∠DCB(两直线平行,同位角相等).
∴∠1=∠2(等量代换).
16.答案:见解析
解析:证明:(1)∵AB∥CD,
∴∠4=∠BAF.
∵∠1=∠2,
∴∠BAF=∠1+∠CAF=∠2+∠CAF=∠DAC,
∴∠4=∠DAC.
(2)∵∠4=∠DAC,∠3=∠4,
∴∠3=∠DAC,∴AD∥BE.
5 / 5
知识点1 综合运用平行线的性质与判定进行计算或说理
1.如图,已知a∥b,∠1=58°,则∠2的大小是( )
A.122°
B.85°
C.58°
D.32°
2.如图,直线EB∥FD,直线c分别交EB、FD于点A、C,∠BAC的平分线交直线FD于点G,若∠2=50°,则∠1的度数是( )
A.50°
B.60°
C.80°
D.100°
3.如图,一块含有30°角的直角三角板的两个顶点放在直尺的对边上.如果∠2=44°,那么∠1的度数是( )
A.14°
B.15°
C.16°
D.17°
4.如图,直线,已知,直线交于一点.若,则等于( )
A. B. C. D.
5.如图,直线被直线所截.若,则的度数是( )
A. B. C. D.
6.如图,若,则下列结论正确的是( )
A. B. C. D.
7.如图,,则____________.
8.如图,,则AB和EF的位置关系为____________.
9.如图所示,和DE分别平分和.试说明:.
解:因为BF和DE分别平分和(已知),所以_____________________(角平分线的定义).
又因为(已知),所以___________(等量代换).
因为(已知),所以(______________).
所以_____________(等量代换).所以(______________).
10.如图,已知.请你观察图形,写出和满足什么数量关系?并说明理由.
知识点2 利用平行线的性质与判定解决实际问題
11.如图所示,要在一条公路的两侧铺设平行管道,已知一侧铺设的角度为,为使管道对接,另一侧铺设的角度大小应为( )
A. B. C. D.
12.如图,在两地挖一条笔直的水渠,从A地测得水渠的走向是北偏西两地同时开工,B地所挖水渠走向应为南偏东_________.
13.一条建设中的高速公路要穿过一山体开挖一条隧道,甲、乙两工程队分别从山体两侧的两点同时开工,现甲队从A点测得道路的走向是北偏东,为了不浪费人力、物力,问乙队在B点处应该按等于多少度开挖,才能够保证隧道准确接通?
14.如图,B处在A处的南偏西45°方向,C处在B处的北偏东80°方向.
(1)求∠ABC的度数;
(2)要使CD∥AB,D处应在C处的什么方向?
15.如图,已知CD⊥AB,GF⊥AB,∠B=∠ADE,试说明∠1=∠2.
16.如图,已知AB∥CD,∠1=∠2,∠3=∠4,求证:
(1)∠4=∠DAC;
(2)AD∥BE.
参考答案
1、B 2.C 3.D
4.答案:C
解析:∵a∥b,∴∠1=∠2,
∵∠1=58°,∴∠2=58°,故选C.
5.答案:C
解析:∵EB∥FD,∴∠BAG=∠2=50°,
∵AG平分∠BAC,∴∠GAC=∠BAG=50°,
∴∠1=180°-∠BAG-∠GAC=80°,故选C.
6.答案:C
解析:根据题意可知∠2+∠3=60°,因为∠2=44°,所以∠3=16°,再根据直尺的对边平行,可知∠1=∠3=16°.
7. 8.平行
9. 两直线平行,内错角相等 同位角相等,两直线平行
10.解:.理由如下:因为,所以.所以.所以.
11.D 12.
13.解:因为指北方向平行,且两点走向形成一条直线,即,所以和就构成了一对同旁内角.所以,即.因此,乙队在B点处应该按开挖.
14.答案:见解析
解析:(1)如图,由题意,得∠FAB=45°.
因为AF∥BE,所以∠FAB=∠ABE=45°,
因为∠EBC=80°,所以∠ABC=35°.
(2)D处在C处的南偏西45°方向.
理由如下:如图,因为CG∥BE,
所以∠GCB=∠EBC=80°.
因为∠GCD=45°,所以∠BCD=35°,
所以∠ABC=∠BCD=35°,所以CD∥AB.
15.答案:见解析
解析:证明:∵∠B=∠ADE(已知),
∴DE∥BC(同位角相等,两直线平行),
∴∠1=∠DCB(两直线平行,内错角相等).
∵CD⊥AB,GF⊥AB,∴∠BDC=90°,∠BFG=90°,
∴CD∥FG(同位角相等,两直线平行),
∴∠2=∠DCB(两直线平行,同位角相等).
∴∠1=∠2(等量代换).
16.答案:见解析
解析:证明:(1)∵AB∥CD,
∴∠4=∠BAF.
∵∠1=∠2,
∴∠BAF=∠1+∠CAF=∠2+∠CAF=∠DAC,
∴∠4=∠DAC.
(2)∵∠4=∠DAC,∠3=∠4,
∴∠3=∠DAC,∴AD∥BE.
5 / 5
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
