人教版七年级数学下册6.3 实数(第一课时) 教案
文档属性
| 名称 | 人教版七年级数学下册6.3 实数(第一课时) 教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 120.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-22 10:43:15 | ||
图片预览

文档简介
《实数》教学设计
【教材】人教版七年级数学下册 6.3实数 第1课时
【教材分析】《实数》是在对算术平方根的研究的基础上,实现数的范围到有理数后的进一步扩展。由激起学生思维的火花,揭示现实空间无限不循环小数的存在,并从本质上理解无理数与有理数的区别。
【学情分析】学生对有理数和平方根已有初步的了解,也已经了解近似数,掌握计算器的简单运用;学生思维仍较直观,无理数显得比较抽象,难以理解;学生对的探索是本课的关键,不仅得到无理数的概念,还有利于培养学生的分析、探索的能力。
【教学目标】
知识与技能
让学生通过研读课文,从感性上认可无理数的存在,并通过探索说出无理数的特征,弄清有理数与无理数的本质区别,了解并掌握无理数、实数的概念以及实数的分类,知道实数与数轴上的点的一一对应关系。
过程与方法
让学生体验利用有理数引出无理数和实数的过程,在教学中渗透类比、数形结合的数学思想方法;通过研读课文教会学生自主学习的方法,掌握数学阅读的学习模式。
情感态度价值观
培养学生热爱数学的情感和勇于发现真理的科学精神,渗透数形结合及分类的思想和对立统一、矛盾转化的辨证唯物主义观点。
【教学重点】无理数、实数的意义;在数轴上表示实数。
【教学难点、关键】无理数与有理数的本质区别;实数与数轴上的点的一一对应关系。
【教学方法】数学总结教学。
【教学过程设计】
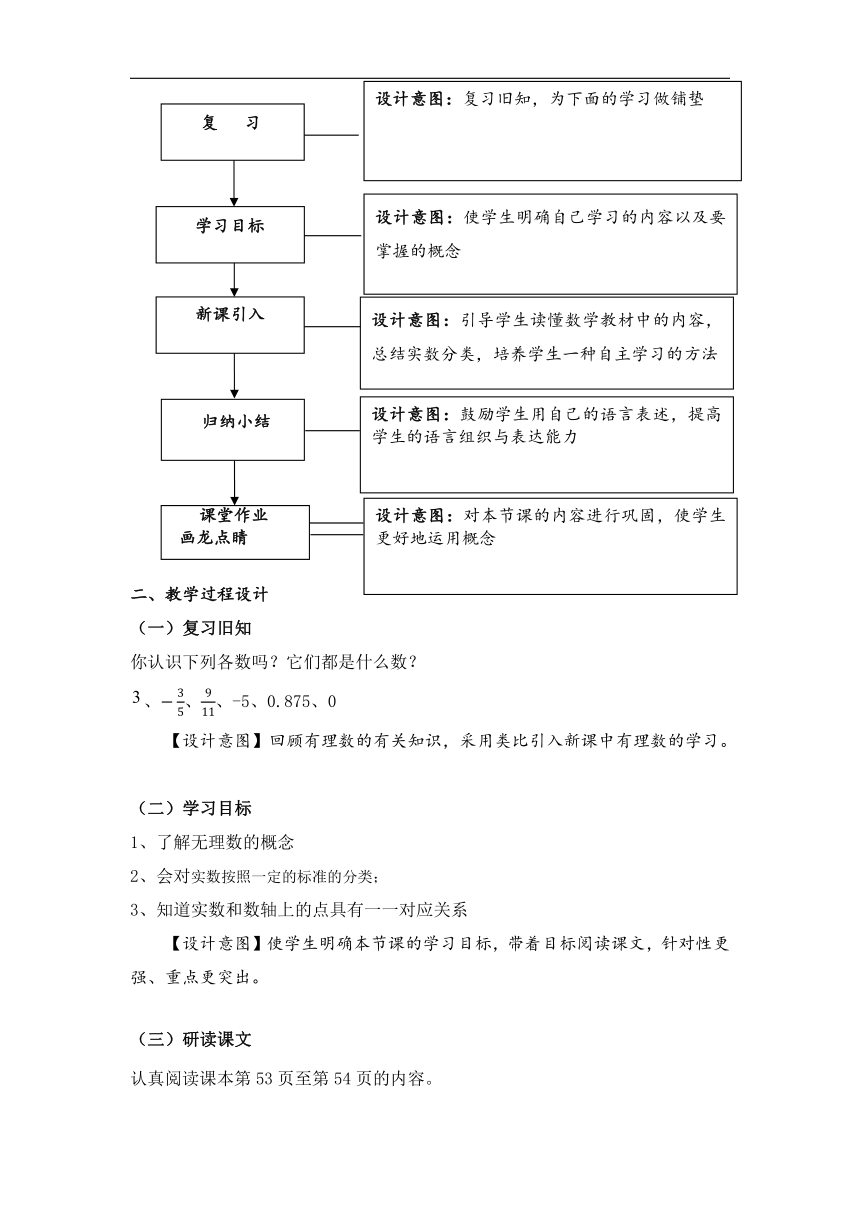
一、教学流程设计
二、教学过程设计
(一)复习旧知
你认识下列各数吗?它们都是什么数?
、、、-5、0.875、0
【设计意图】回顾有理数的有关知识,采用类比引入新课中有理数的学习。
(二)学习目标
1、了解无理数的概念
2、会对实数按照一定的标准的分类;
3、知道实数和数轴上的点具有一一对应关系
【设计意图】使学生明确本节课的学习目标,带着目标阅读课文,针对性更强、重点更突出。
(三)研读课文
认真阅读课本第53页至第54页的内容。
【设计意图】书本是新课学习的基础。
(四)新课导入
1、观察下列各数的小数形式:
【设计意图】回顾平方根、立方根的有关知识,让学生感受实数的存在并引入新课。
2、完成下面练习,并体验知识点的形成过程。
3、使用计算器计算,把下列有理数写成小数的形式,你有什么发现?
=______,=______,=______, =______, =______, =______。
我们发现,上面的有理数都可以写成________ 或者 的形式。
归纳 事实上,任何一个 都可以写成有限小数或无限循环小数的形式。反过来, 任何__________________________也都是有理数。
观察 我们知道,很多数的平方根和立方根都是无限不循环小数,无限不循环小数又叫做 _ __。例如 , , , 等都是 ____ 。
也是 。
结论 有理数和无理数统称为 。
试一试 我们学过的数可以这样分类:
像有理数一样,无理数也有正负之分。例如,,是 ,,,是 。由于非0有理数和无理数都有正负之分,所以实数也可以这样分类:
【设计意图】此题引导学生自主阅读课文,指导学生一种有效的学习方法,使学生不至于盲目自学而是有据可依,在感官上认识无理数和实数,了解无理数和实数的概念,由有理数和无理数的比较体验数学分类思想方法。
4、 合作探究 达成目标(此部分为课堂展示部分,结合书本知识)
我们知道,每个有理数都可以用数轴上的点来表示,那么无理数是否也可以用数轴上的点表示出来呢?你能在数轴上找到表示无理数的点吗?
从课本图6.3-1中可以看出的长是 ,所以对应的数是 .
总结 (1)每个有理数都可以用数轴上的点来表示。
事实上,每一个 也都可以用数轴上的 表示出来。这就是说,数轴上的点有些表示 数,有些表示 数。
(2)当从有理数扩充到实数以后,实数与数轴上的点就是 ___ 的,即每一个实数都可以用数轴上的 _来表示;反过来,数轴上的每一个点都是表示一个 。
【设计意图】让学生继续阅读课文,结合数轴进一步探究、理解实数的性质,使学生在阅读中思考,在思考中体验数形结合的数学思想方法。
四、归纳小结
(一)谈谈本节课的收获是什么?
(二)你认为本节课需要注意的地方有哪些?
【设计意图】让学生回顾本节课的重点内容,理解实数的概念、性质,培养学生梳理知识的能力、归纳能力和表达能力。
五、课堂作业
1、下列各数 ,, , , , 中,有理数的个数有( )
A 2个 B 3个 C 4个 D 5个
2、把下列各数分别填入相应的集合里:
正有理数{ }
负有理数{ }
正无理数{ }
负无理数{ }
3判断题
(1)无理数是无限小数,无限小数就是无理数。 ( )
(2)无理数包括正无理数,0,负无理数 ( )
(3)带根号的数都是无理数,不带根号的数都是有理数 ( )
(4)是一个分数 ( )
【设计意图】强化训练分层处理有较大的弹性,体现了练习的巩固性和发展性原则,尊重学生的个体差异,满足多样化的学习需要,从而让不同的学生在数学上得到不同的发展。
【教材】人教版七年级数学下册 6.3实数 第1课时
【教材分析】《实数》是在对算术平方根的研究的基础上,实现数的范围到有理数后的进一步扩展。由激起学生思维的火花,揭示现实空间无限不循环小数的存在,并从本质上理解无理数与有理数的区别。
【学情分析】学生对有理数和平方根已有初步的了解,也已经了解近似数,掌握计算器的简单运用;学生思维仍较直观,无理数显得比较抽象,难以理解;学生对的探索是本课的关键,不仅得到无理数的概念,还有利于培养学生的分析、探索的能力。
【教学目标】
知识与技能
让学生通过研读课文,从感性上认可无理数的存在,并通过探索说出无理数的特征,弄清有理数与无理数的本质区别,了解并掌握无理数、实数的概念以及实数的分类,知道实数与数轴上的点的一一对应关系。
过程与方法
让学生体验利用有理数引出无理数和实数的过程,在教学中渗透类比、数形结合的数学思想方法;通过研读课文教会学生自主学习的方法,掌握数学阅读的学习模式。
情感态度价值观
培养学生热爱数学的情感和勇于发现真理的科学精神,渗透数形结合及分类的思想和对立统一、矛盾转化的辨证唯物主义观点。
【教学重点】无理数、实数的意义;在数轴上表示实数。
【教学难点、关键】无理数与有理数的本质区别;实数与数轴上的点的一一对应关系。
【教学方法】数学总结教学。
【教学过程设计】
一、教学流程设计
二、教学过程设计
(一)复习旧知
你认识下列各数吗?它们都是什么数?
、、、-5、0.875、0
【设计意图】回顾有理数的有关知识,采用类比引入新课中有理数的学习。
(二)学习目标
1、了解无理数的概念
2、会对实数按照一定的标准的分类;
3、知道实数和数轴上的点具有一一对应关系
【设计意图】使学生明确本节课的学习目标,带着目标阅读课文,针对性更强、重点更突出。
(三)研读课文
认真阅读课本第53页至第54页的内容。
【设计意图】书本是新课学习的基础。
(四)新课导入
1、观察下列各数的小数形式:
【设计意图】回顾平方根、立方根的有关知识,让学生感受实数的存在并引入新课。
2、完成下面练习,并体验知识点的形成过程。
3、使用计算器计算,把下列有理数写成小数的形式,你有什么发现?
=______,=______,=______, =______, =______, =______。
我们发现,上面的有理数都可以写成________ 或者 的形式。
归纳 事实上,任何一个 都可以写成有限小数或无限循环小数的形式。反过来, 任何__________________________也都是有理数。
观察 我们知道,很多数的平方根和立方根都是无限不循环小数,无限不循环小数又叫做 _ __。例如 , , , 等都是 ____ 。
也是 。
结论 有理数和无理数统称为 。
试一试 我们学过的数可以这样分类:
像有理数一样,无理数也有正负之分。例如,,是 ,,,是 。由于非0有理数和无理数都有正负之分,所以实数也可以这样分类:
【设计意图】此题引导学生自主阅读课文,指导学生一种有效的学习方法,使学生不至于盲目自学而是有据可依,在感官上认识无理数和实数,了解无理数和实数的概念,由有理数和无理数的比较体验数学分类思想方法。
4、 合作探究 达成目标(此部分为课堂展示部分,结合书本知识)
我们知道,每个有理数都可以用数轴上的点来表示,那么无理数是否也可以用数轴上的点表示出来呢?你能在数轴上找到表示无理数的点吗?
从课本图6.3-1中可以看出的长是 ,所以对应的数是 .
总结 (1)每个有理数都可以用数轴上的点来表示。
事实上,每一个 也都可以用数轴上的 表示出来。这就是说,数轴上的点有些表示 数,有些表示 数。
(2)当从有理数扩充到实数以后,实数与数轴上的点就是 ___ 的,即每一个实数都可以用数轴上的 _来表示;反过来,数轴上的每一个点都是表示一个 。
【设计意图】让学生继续阅读课文,结合数轴进一步探究、理解实数的性质,使学生在阅读中思考,在思考中体验数形结合的数学思想方法。
四、归纳小结
(一)谈谈本节课的收获是什么?
(二)你认为本节课需要注意的地方有哪些?
【设计意图】让学生回顾本节课的重点内容,理解实数的概念、性质,培养学生梳理知识的能力、归纳能力和表达能力。
五、课堂作业
1、下列各数 ,, , , , 中,有理数的个数有( )
A 2个 B 3个 C 4个 D 5个
2、把下列各数分别填入相应的集合里:
正有理数{ }
负有理数{ }
正无理数{ }
负无理数{ }
3判断题
(1)无理数是无限小数,无限小数就是无理数。 ( )
(2)无理数包括正无理数,0,负无理数 ( )
(3)带根号的数都是无理数,不带根号的数都是有理数 ( )
(4)是一个分数 ( )
【设计意图】强化训练分层处理有较大的弹性,体现了练习的巩固性和发展性原则,尊重学生的个体差异,满足多样化的学习需要,从而让不同的学生在数学上得到不同的发展。
