人教版八年级数学上册 12.3 角的平分线性质的应用 教学设计
文档属性
| 名称 | 人教版八年级数学上册 12.3 角的平分线性质的应用 教学设计 | 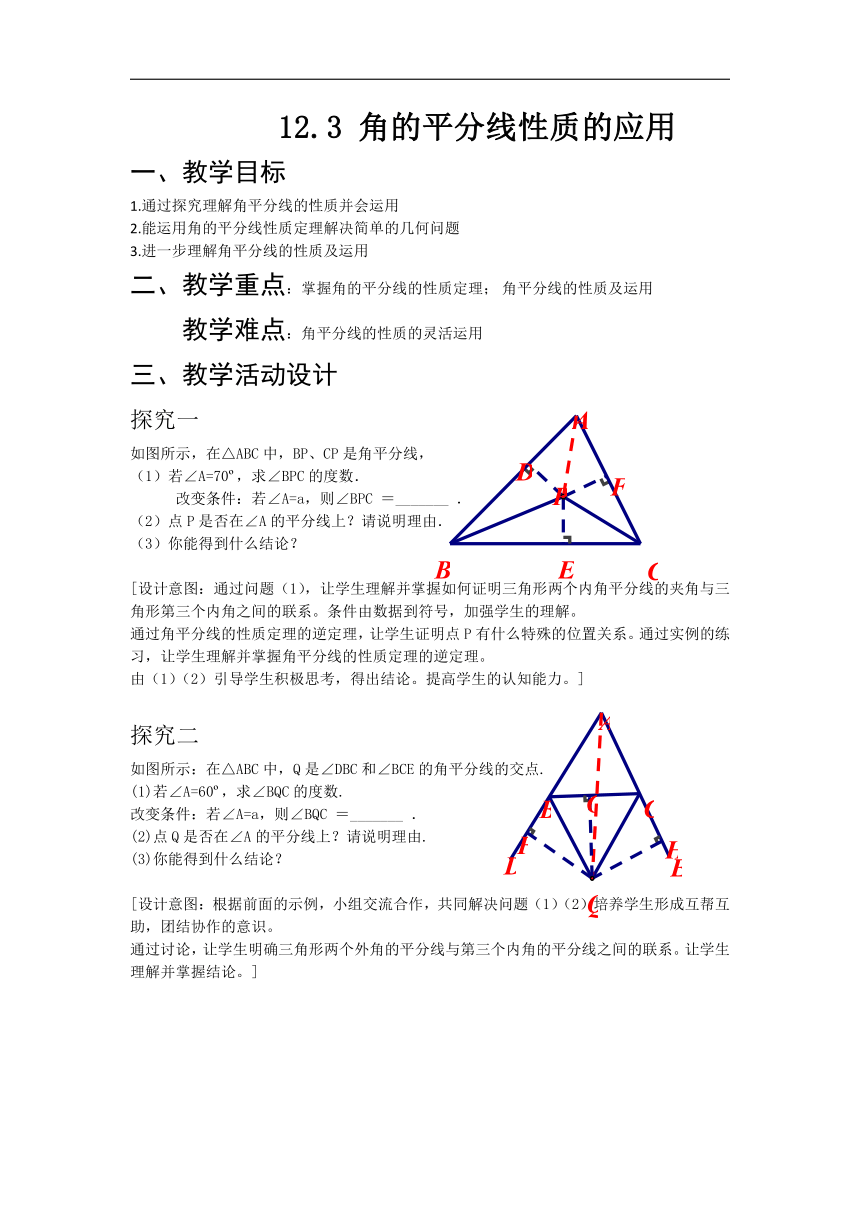 | |
| 格式 | doc | ||
| 文件大小 | 230.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-22 10:50:24 | ||
图片预览

文档简介
12.3 角的平分线性质的应用
一、教学目标
1.通过探究理解角平分线的性质并会运用
2.能运用角的平分线性质定理解决简单的几何问题
3.进一步理解角平分线的性质及运用
二、教学重点:掌握角的平分线的性质定理; 角平分线的性质及运用
教学难点:角平分线的性质的灵活运用
三、教学活动设计
探究一
如图所示,在△ABC中,BP、CP是角平分线,
(1)若∠A=70 ,求∠BPC的度数.
改变条件:若∠A=a,则∠BPC =_______ .
(2)点P是否在∠A的平分线上?请说明理由.
(3)你能得到什么结论?
[设计意图:通过问题(1),让学生理解并掌握如何证明三角形两个内角平分线的夹角与三角形第三个内角之间的联系。条件由数据到符号,加强学生的理解。
通过角平分线的性质定理的逆定理,让学生证明点P有什么特殊的位置关系。通过实例的练习,让学生理解并掌握角平分线的性质定理的逆定理。
由(1)(2)引导学生积极思考,得出结论。提高学生的认知能力。]
探究二
如图所示:在△ABC中,Q是∠DBC和∠BCE的角平分线的交点.
(1)若∠A=60 ,求∠BQC的度数.
改变条件:若∠A=a,则∠BQC =_______ .
(2)点Q是否在∠A的平分线上?请说明理由.
(3)你能得到什么结论?
[设计意图:根据前面的示例,小组交流合作,共同解决问题(1)(2)培养学生形成互帮互助,团结协作的意识。
通过讨论,让学生明确三角形两个外角的平分线与第三个内角的平分线之间的联系。让学生理解并掌握结论。]
思考
由应用一、二你还能得到哪些结论?
1.∠BPC+ ∠BQC=180°
2.A、P、Q三点共线
3.∠BQA = ∠BCA
4.到三角形三边距离相等的点有4个
[设计意图:配合老师的引导与提示,认真思考,积极回答。重点培养学生的解题思路以及归纳概括能力。]
练习一
如图,有三条公路两两相交于A、B、C点处,现计划修建一个加油站,要求到三条公路的距离相等,那么该如何选择加油站的位置?
[设计意图:让学生做一些针对性较强的练习,提高认知。通过具体的练习题,让学生能做到举一反三。]
练习二
如图,在△ABC中,∠ABC=60 ,AD、CE分别平分∠BAC、∠ACB,且AD、CE交于点O.
(1)求∠COD的度数;
(2)求证:OD=OE
[设计意图:通过实例的练习,让学生理解并掌握如何利用角平分线的性质解决各种问题。让学生做一些针对性较强的练习,提高认知。教师给予一定的提示以及肯定和鼓励激发他们学习的积极性和主动性。]
四、教学反思
1、通过具体情境使学生能够比较容易的运用定理
许多学生学习了定理后,遇到相对应的题目往往不知道该怎样用定理,通过一些对应的题目,或者用数学语言给出条件,让学生得出结论,并说出相应的定理,可以强化学生对定理的运用能力。
2、注重分析思路,学生学会思考问题,注重书写格式,让学生学会清楚的表达思考的过程。在证明的选题上,注意了减缓坡度,循序渐进。
E
D
F
P
B
A
C
D
E
F
H
G
Q
A
B
C
D
E
P
Q
A
B
C
P
N
M
O
E
D
A
C
B
一、教学目标
1.通过探究理解角平分线的性质并会运用
2.能运用角的平分线性质定理解决简单的几何问题
3.进一步理解角平分线的性质及运用
二、教学重点:掌握角的平分线的性质定理; 角平分线的性质及运用
教学难点:角平分线的性质的灵活运用
三、教学活动设计
探究一
如图所示,在△ABC中,BP、CP是角平分线,
(1)若∠A=70 ,求∠BPC的度数.
改变条件:若∠A=a,则∠BPC =_______ .
(2)点P是否在∠A的平分线上?请说明理由.
(3)你能得到什么结论?
[设计意图:通过问题(1),让学生理解并掌握如何证明三角形两个内角平分线的夹角与三角形第三个内角之间的联系。条件由数据到符号,加强学生的理解。
通过角平分线的性质定理的逆定理,让学生证明点P有什么特殊的位置关系。通过实例的练习,让学生理解并掌握角平分线的性质定理的逆定理。
由(1)(2)引导学生积极思考,得出结论。提高学生的认知能力。]
探究二
如图所示:在△ABC中,Q是∠DBC和∠BCE的角平分线的交点.
(1)若∠A=60 ,求∠BQC的度数.
改变条件:若∠A=a,则∠BQC =_______ .
(2)点Q是否在∠A的平分线上?请说明理由.
(3)你能得到什么结论?
[设计意图:根据前面的示例,小组交流合作,共同解决问题(1)(2)培养学生形成互帮互助,团结协作的意识。
通过讨论,让学生明确三角形两个外角的平分线与第三个内角的平分线之间的联系。让学生理解并掌握结论。]
思考
由应用一、二你还能得到哪些结论?
1.∠BPC+ ∠BQC=180°
2.A、P、Q三点共线
3.∠BQA = ∠BCA
4.到三角形三边距离相等的点有4个
[设计意图:配合老师的引导与提示,认真思考,积极回答。重点培养学生的解题思路以及归纳概括能力。]
练习一
如图,有三条公路两两相交于A、B、C点处,现计划修建一个加油站,要求到三条公路的距离相等,那么该如何选择加油站的位置?
[设计意图:让学生做一些针对性较强的练习,提高认知。通过具体的练习题,让学生能做到举一反三。]
练习二
如图,在△ABC中,∠ABC=60 ,AD、CE分别平分∠BAC、∠ACB,且AD、CE交于点O.
(1)求∠COD的度数;
(2)求证:OD=OE
[设计意图:通过实例的练习,让学生理解并掌握如何利用角平分线的性质解决各种问题。让学生做一些针对性较强的练习,提高认知。教师给予一定的提示以及肯定和鼓励激发他们学习的积极性和主动性。]
四、教学反思
1、通过具体情境使学生能够比较容易的运用定理
许多学生学习了定理后,遇到相对应的题目往往不知道该怎样用定理,通过一些对应的题目,或者用数学语言给出条件,让学生得出结论,并说出相应的定理,可以强化学生对定理的运用能力。
2、注重分析思路,学生学会思考问题,注重书写格式,让学生学会清楚的表达思考的过程。在证明的选题上,注意了减缓坡度,循序渐进。
E
D
F
P
B
A
C
D
E
F
H
G
Q
A
B
C
D
E
P
Q
A
B
C
P
N
M
O
E
D
A
C
B
