人教版八年级数学上册12.2.3三角形全等的判定 教学设计
文档属性
| 名称 | 人教版八年级数学上册12.2.3三角形全等的判定 教学设计 |

|
|
| 格式 | docx | ||
| 文件大小 | 977.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-22 00:00:00 | ||
图片预览

文档简介
§12.2.3三角形全等的判定
一、教学目标:
1、掌握三角形全等的“角边角”“角角边”条件.
2、能运用全等三角形的条件,解决简单的推理证明问题.
二、教学重难点:
重点:掌握三角形全等的“角边角”“角角边”条件
难点:运用全等三角形的条件进行推理证明
三、教学准备: 三角板
四、教学方法:合作、探究
五、教学过程:
(一)创设情境:
如图,小明不慎将一块三角形模具打碎为两块,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形模具吗 如果可以,带哪块去合适 你能说明其中理由吗
1、问题导入
如果知道两个三角形的两个角及一条边分别对应相等,这两个三角形一定全等吗?
这时应该有两种不同的情况:
(1)两个角及两角的夹边;
(2)两个角及其中一角的对边
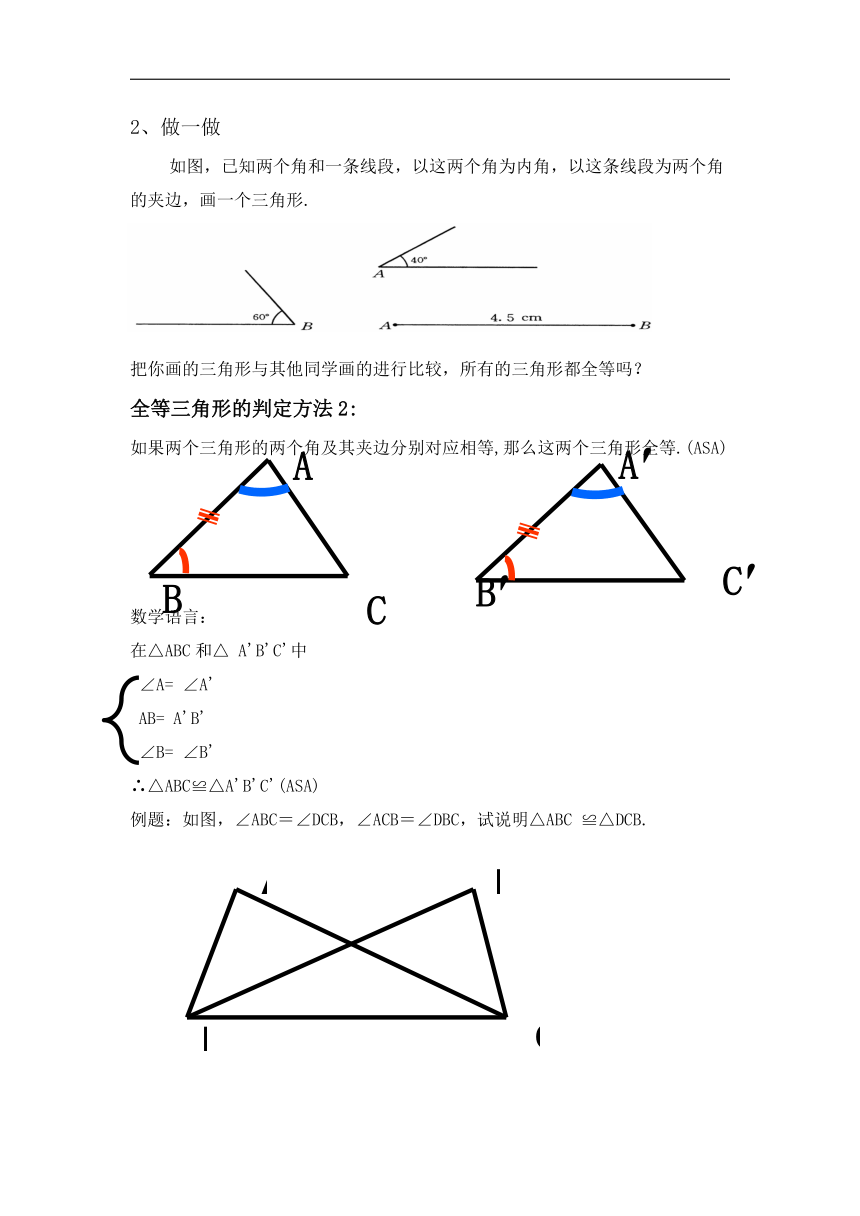
2、做一做
如图,已知两个角和一条线段,以这两个角为内角,以这条线段为两个角的夹边,画一个三角形.
把你画的三角形与其他同学画的进行比较,所有的三角形都全等吗?
全等三角形的判定方法2:
如果两个三角形的两个角及其夹边分别对应相等,那么这两个三角形全等.(ASA)
数学语言:
在△ABC和△ A'B'C'中
∠A= ∠A'
AB= A'B'
∠B= ∠B'
∴△ABC≌△A'B'C'(ASA)
例题:如图,∠ABC=∠DCB,∠ACB=∠DBC,试说明△ABC ≌△DCB.
(二)探究:
思考:如果两个三角形有两个角和其中一个角的对边分别对应相等,那么这两个三角形是否全等
全等三角形的判定方法3:
如果两个三角形的两个角及其中一个角的对边分别对应相等,那么这两个三角形全等.(AAS)
数学语言:
在△ABC和△ A'B'C'中
∠A= ∠A'
∠B= ∠B'
BC= B'C'
∴△ABC≌△ A'B'C'(AAS)
总结:
(1)两角和它们的夹边对应相等的两个三角形全等,简写成“角边角”或“ASA”
(ASA)
(2)两角和其中一角的对边对应相等的两个三角形全等,简写成“角角边”或“AAS”
(三)练习
1. 根据题目条件,判别下面的两个三角形是否全等,并说明理由.
2.要使下列各对三角形全等,需要增加什么条件?
(1) (2)
3.如图,已知AB与CD 相交于O,∠A=∠D,CO=BO,说明△AOC与△DOB全等的理由.
思考题:
4. 已知:如图,△ABC ≌△A’B’C’,AD、A’D’ 分别是△ABC 和△A’B’C’的高。试说明AD= A’D’ ,并用一句话说出你的发现。
拓展:
1、全等三角形对应边上的中线相等?
2、全等三角形对应角的平分线相等?
六、小结:
本节课我们主要学习了有关全等三角形的“两角一边”识别方法,有两种情况:
1. 两个角及两角的夹边;
2.两个角及其中一角的对边。
到目前为此,我们共学了几种识别三角形全等的方法?
七、作业
1.P44习题 第4 5 11题
2.基础训练P32-34第二课时
一、教学目标:
1、掌握三角形全等的“角边角”“角角边”条件.
2、能运用全等三角形的条件,解决简单的推理证明问题.
二、教学重难点:
重点:掌握三角形全等的“角边角”“角角边”条件
难点:运用全等三角形的条件进行推理证明
三、教学准备: 三角板
四、教学方法:合作、探究
五、教学过程:
(一)创设情境:
如图,小明不慎将一块三角形模具打碎为两块,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形模具吗 如果可以,带哪块去合适 你能说明其中理由吗
1、问题导入
如果知道两个三角形的两个角及一条边分别对应相等,这两个三角形一定全等吗?
这时应该有两种不同的情况:
(1)两个角及两角的夹边;
(2)两个角及其中一角的对边
2、做一做
如图,已知两个角和一条线段,以这两个角为内角,以这条线段为两个角的夹边,画一个三角形.
把你画的三角形与其他同学画的进行比较,所有的三角形都全等吗?
全等三角形的判定方法2:
如果两个三角形的两个角及其夹边分别对应相等,那么这两个三角形全等.(ASA)
数学语言:
在△ABC和△ A'B'C'中
∠A= ∠A'
AB= A'B'
∠B= ∠B'
∴△ABC≌△A'B'C'(ASA)
例题:如图,∠ABC=∠DCB,∠ACB=∠DBC,试说明△ABC ≌△DCB.
(二)探究:
思考:如果两个三角形有两个角和其中一个角的对边分别对应相等,那么这两个三角形是否全等
全等三角形的判定方法3:
如果两个三角形的两个角及其中一个角的对边分别对应相等,那么这两个三角形全等.(AAS)
数学语言:
在△ABC和△ A'B'C'中
∠A= ∠A'
∠B= ∠B'
BC= B'C'
∴△ABC≌△ A'B'C'(AAS)
总结:
(1)两角和它们的夹边对应相等的两个三角形全等,简写成“角边角”或“ASA”
(ASA)
(2)两角和其中一角的对边对应相等的两个三角形全等,简写成“角角边”或“AAS”
(三)练习
1. 根据题目条件,判别下面的两个三角形是否全等,并说明理由.
2.要使下列各对三角形全等,需要增加什么条件?
(1) (2)
3.如图,已知AB与CD 相交于O,∠A=∠D,CO=BO,说明△AOC与△DOB全等的理由.
思考题:
4. 已知:如图,△ABC ≌△A’B’C’,AD、A’D’ 分别是△ABC 和△A’B’C’的高。试说明AD= A’D’ ,并用一句话说出你的发现。
拓展:
1、全等三角形对应边上的中线相等?
2、全等三角形对应角的平分线相等?
六、小结:
本节课我们主要学习了有关全等三角形的“两角一边”识别方法,有两种情况:
1. 两个角及两角的夹边;
2.两个角及其中一角的对边。
到目前为此,我们共学了几种识别三角形全等的方法?
七、作业
1.P44习题 第4 5 11题
2.基础训练P32-34第二课时
