北师大版八年级下册 2.5 一元一次不等式与一次函数 课件(共27张)
文档属性
| 名称 | 北师大版八年级下册 2.5 一元一次不等式与一次函数 课件(共27张) |  | |
| 格式 | zip | ||
| 文件大小 | 751.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-22 11:37:27 | ||
图片预览





文档简介
(共27张PPT)
第二章 一元一次不等式与 一元一次不等式组
2.5 一元一次不等式 与一次函数
·
1.通过作函数图象、观察函数图象,进一步理解函数的概念,并从中初步体会一元一次不等式与一次函数的内在联系.
2.通过具体问题初步体会一次函数的变化规律与一元一次不等式的解集的联系.
3.感知不等式、函数、方程的不同作用与内在联系.
·
重点:初步建立“数”(一元一次不等式)与“形”(一次
函数)之间的关系,根据一次函数图象求一元一次
不等式的解集.
难点:理解一元一次不等式与一次函数的关系.
利用图象
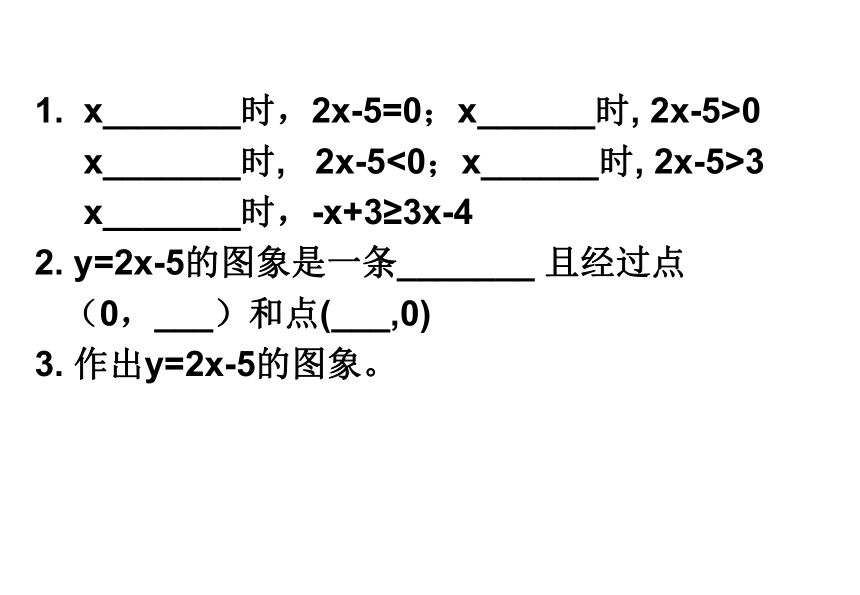
1. x_______时,2x-5=0;x______时, 2x-5>0
x_______时, 2x-5<0;x______时, 2x-5>3
x_______时,-x+3≥3x-4
2. y=2x-5的图象是一条_______ 且经过点
(0,___)和点(___,0)
3. 作出y=2x-5的图象。
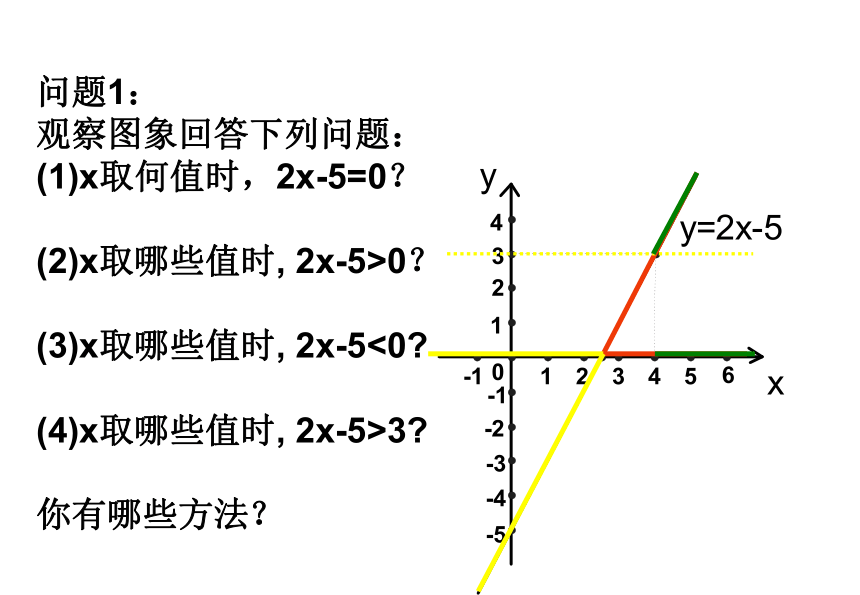
问题1:
观察图象回答下列问题:
x取何值时,2x-5=0?
x取哪些值时, 2x-5>0?
x取哪些值时, 2x-5<0
x取哪些值时, 2x-5>3
你有哪些方法?
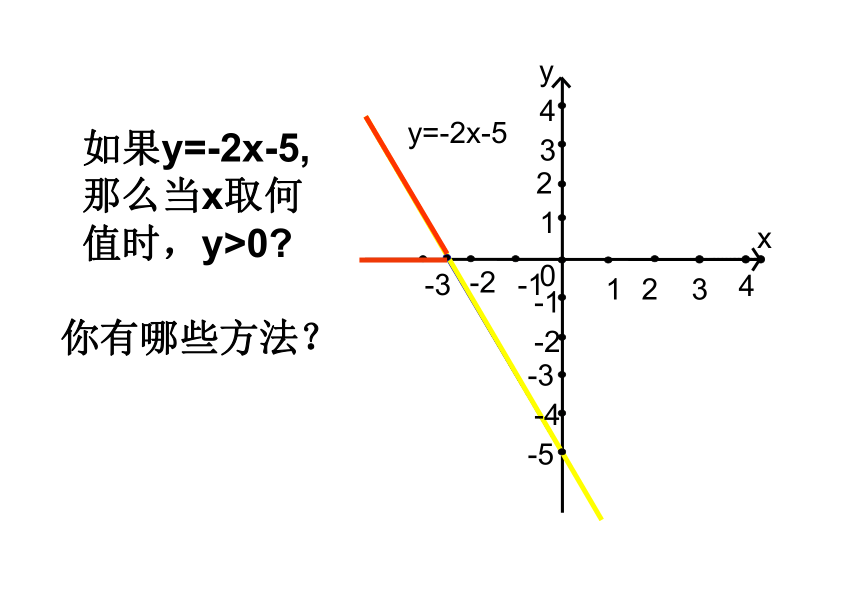
如果y=-2x-5,
那么当x取何
值时,y>0
你有哪些方法?
1
2
3
4
-1
-2
-3
-1
-2
-3
-4
0
1
2
3
4
x
-5
y
y=-2x-5
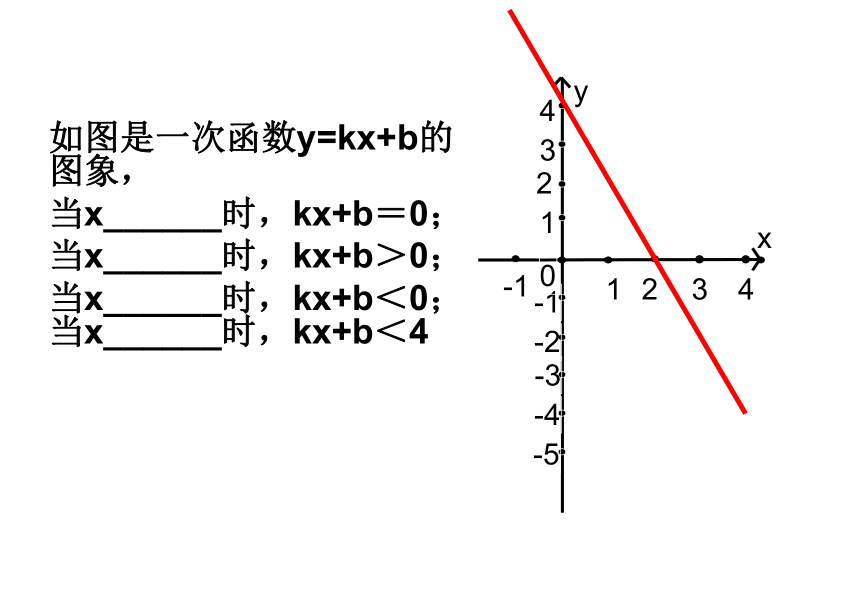
如图是一次函数y=kx+b的图象,
当x______时,kx+b=0;
当x______时,kx+b>0;
当x______时,kx+b<0;当x______时,kx+b<4
1
2
3
4
-1
-1
-2
-3
-4
0
1
2
3
4
-5
y
x
一元一次不等式与一次函数在 决策型应用题中的应用
1.根据实际问题设求知数x, y1, y2
2.列出y1, y2与x的函数关系式
3. 分别讨论三种情况,解出方程和不等式
4.写出结论
C
B
x≤2
>1500千米
【例1】已知一次函数的图象过点A(1,4)、B(-1,0)两点,求函数解析式并画出它的图象,并求:(1)x为何值时,y>0,y=0,y<0;(2)当-3<x<0时,y的取值范围;(3)当-2≤y≤2时,x的取值范围.
解析:(1)把A(1,4)、B(-1,0)代入y=kx+b可求出解析式;(2)画出图象结合图象解决,当-3<x<0时,-4<y<2;当-2≤y≤2时,-2≤x≤0.
解:设一次函数的解析式为y=kx+b,则k+b=4,-k+b=0,∴k=2,b=2.∴y=2x+2.∴一次函数的图象如图,由图象可知:(1)当x>-1时,y>0;当x=-1时,y=0;当x<-1时,y<0;(2)当-3<x<0时,-4<y<2;(3)当-2≤y≤2时,-2≤x≤0.
解析:由直线y=kx+b经过A(-2,-1)和B(-3,0),可求出解析式:y=-x-3,从而12x<-x-3,-x-3<0,解得-3<x<-2.
【例2】如图,直线y=kx+b经过点A(-2,-1)和B(-3,0)两点,则不等式12x<kx+b<0的解集为 .
-3<x<-2
解析:由于题设中商场投资情况是未知的,不能直接比较,应根据投资情况列函数解析式,分类进行比较判断.
【例3】某市场计划投入一笔资金采购一批紧俏商品,经过市场调查发现,如果月初出售,可获利15%,并可用本和利再投资其他商品,到月末又可获利10%;如果月末出售,可获利30%,但要付出仓库费用700元.根据商场情况,如何购销获利较多?
解:设商场投资x元,在月初出售,到月末可获利y1元,在月末出售,可获利y2元,则y1=(1+10%)(x+15%x)-x=0.265x,y2=0.3x-700.利用函数图象比较大小,在直角坐标系中,作出两函数的图象如图所示,得两图象的交点横坐标为20000.由图象可知x>20000时,选择月末出售获利较多,当x=20000时,选择两者任一种都一样;当x<20000时,选择月初销售获利较多.
【例4】某校需要添置部分办公桌,现从两个家具店得到信息:同样的办公桌每张标价均为225元,甲店的优惠条件是购买办公桌不超过10张,按标价付费,超过10张,超过的部分打8折;乙店的优惠条件是购买办公桌一律打9折,若该校计划购买x张办公桌,在甲、乙两店购买所需费用分别为y1、y2(元).(1)试分别写出y1、y2与x之间的函数关系式;(2)请你帮助该校选择在哪个家具店购买办公桌比较合算.解析:由题意知,费用的多少跟购买办公室的数量有关,因此可根据题意设出的办公桌数量x张,分别写出两个家具店所需费用的函数关系式,建立函数模型,然后作比较,分y1>y2,y1=y2,y1<y2讨论.
解析:由题意知,费用的多少跟购买办公室的数量有关,因此可根据题意设出的办公桌数量x张,分别写出两个家具店所需费用的函数关系式,建立函数模型,然后作比较,分y1>y2,y1=y2,y1<y2讨论.
解:解法1:(1)(解析法)根据题意得,当x>10时,y1=225×10+(x-10)×225×0.8=180x+450,y2=225×0.9x=202.5x;当x≤10时,y1=225x,y2=225×0.9x=202.5x;(2)由(1)可知当x≤10时,去乙店购买合算.当x>10时,若y1>y2,则去乙店购买合算,即180x+450>202.5x,解得x<20;若y1=y2,则去甲、乙两店收费相同,即180x+450=202.5x,解得x=20;若y1<y2,则去甲店购买合算,即180x+450<202.5x,解得x>20.答:该校购买办公桌少于20张时,去乙店购买合算;该校购买办公桌20张时,甲、乙两店收费相同;该校购买办公桌多于20张时,去甲店购买合算.
解法2:(图象法)(1)同解法1.(2)当x≤10时同解法1,当x>10时,设去甲、乙两店购买的费用差为y元,则y=y1-y2=(180x+450)-202.5x=-22.5x+450.画出一次函数y=-22.5x+450的图象如图所示,它与x轴的交点为(20,0),由图象可知:①当x<20时,y>0,即y1>y2,去乙店购买合算;②当x=20时,y=0,即y1=y2,甲、乙两店费用相同;③当x>20时,y<0,即y1<y2,去甲店购买合算.答:该校购买办公桌少于20张时,去乙店购买合算;该校购买办公桌20张时,甲、乙两店费用相同;该校购买办公桌多于20张时,去甲店购买合算.
A
A
(1,0)
x<3
解:画图略;(1)x>2
(2)-1≤x≤5
理解函数的概念,并从中初步体会一元一次不等式与一次函数的内在联系.通过具体问题初步体会一次函数的变化规律与一元一次不等式的解集的联系.使学生从整体上认识不等式,感受函数、方程、不等式的作用.
第二章 一元一次不等式与 一元一次不等式组
2.5 一元一次不等式 与一次函数
·
1.通过作函数图象、观察函数图象,进一步理解函数的概念,并从中初步体会一元一次不等式与一次函数的内在联系.
2.通过具体问题初步体会一次函数的变化规律与一元一次不等式的解集的联系.
3.感知不等式、函数、方程的不同作用与内在联系.
·
重点:初步建立“数”(一元一次不等式)与“形”(一次
函数)之间的关系,根据一次函数图象求一元一次
不等式的解集.
难点:理解一元一次不等式与一次函数的关系.
利用图象
1. x_______时,2x-5=0;x______时, 2x-5>0
x_______时, 2x-5<0;x______时, 2x-5>3
x_______时,-x+3≥3x-4
2. y=2x-5的图象是一条_______ 且经过点
(0,___)和点(___,0)
3. 作出y=2x-5的图象。
问题1:
观察图象回答下列问题:
x取何值时,2x-5=0?
x取哪些值时, 2x-5>0?
x取哪些值时, 2x-5<0
x取哪些值时, 2x-5>3
你有哪些方法?
如果y=-2x-5,
那么当x取何
值时,y>0
你有哪些方法?
1
2
3
4
-1
-2
-3
-1
-2
-3
-4
0
1
2
3
4
x
-5
y
y=-2x-5
如图是一次函数y=kx+b的图象,
当x______时,kx+b=0;
当x______时,kx+b>0;
当x______时,kx+b<0;当x______时,kx+b<4
1
2
3
4
-1
-1
-2
-3
-4
0
1
2
3
4
-5
y
x
一元一次不等式与一次函数在 决策型应用题中的应用
1.根据实际问题设求知数x, y1, y2
2.列出y1, y2与x的函数关系式
3. 分别讨论三种情况,解出方程和不等式
4.写出结论
C
B
x≤2
>1500千米
【例1】已知一次函数的图象过点A(1,4)、B(-1,0)两点,求函数解析式并画出它的图象,并求:(1)x为何值时,y>0,y=0,y<0;(2)当-3<x<0时,y的取值范围;(3)当-2≤y≤2时,x的取值范围.
解析:(1)把A(1,4)、B(-1,0)代入y=kx+b可求出解析式;(2)画出图象结合图象解决,当-3<x<0时,-4<y<2;当-2≤y≤2时,-2≤x≤0.
解:设一次函数的解析式为y=kx+b,则k+b=4,-k+b=0,∴k=2,b=2.∴y=2x+2.∴一次函数的图象如图,由图象可知:(1)当x>-1时,y>0;当x=-1时,y=0;当x<-1时,y<0;(2)当-3<x<0时,-4<y<2;(3)当-2≤y≤2时,-2≤x≤0.
解析:由直线y=kx+b经过A(-2,-1)和B(-3,0),可求出解析式:y=-x-3,从而12x<-x-3,-x-3<0,解得-3<x<-2.
【例2】如图,直线y=kx+b经过点A(-2,-1)和B(-3,0)两点,则不等式12x<kx+b<0的解集为 .
-3<x<-2
解析:由于题设中商场投资情况是未知的,不能直接比较,应根据投资情况列函数解析式,分类进行比较判断.
【例3】某市场计划投入一笔资金采购一批紧俏商品,经过市场调查发现,如果月初出售,可获利15%,并可用本和利再投资其他商品,到月末又可获利10%;如果月末出售,可获利30%,但要付出仓库费用700元.根据商场情况,如何购销获利较多?
解:设商场投资x元,在月初出售,到月末可获利y1元,在月末出售,可获利y2元,则y1=(1+10%)(x+15%x)-x=0.265x,y2=0.3x-700.利用函数图象比较大小,在直角坐标系中,作出两函数的图象如图所示,得两图象的交点横坐标为20000.由图象可知x>20000时,选择月末出售获利较多,当x=20000时,选择两者任一种都一样;当x<20000时,选择月初销售获利较多.
【例4】某校需要添置部分办公桌,现从两个家具店得到信息:同样的办公桌每张标价均为225元,甲店的优惠条件是购买办公桌不超过10张,按标价付费,超过10张,超过的部分打8折;乙店的优惠条件是购买办公桌一律打9折,若该校计划购买x张办公桌,在甲、乙两店购买所需费用分别为y1、y2(元).(1)试分别写出y1、y2与x之间的函数关系式;(2)请你帮助该校选择在哪个家具店购买办公桌比较合算.解析:由题意知,费用的多少跟购买办公室的数量有关,因此可根据题意设出的办公桌数量x张,分别写出两个家具店所需费用的函数关系式,建立函数模型,然后作比较,分y1>y2,y1=y2,y1<y2讨论.
解析:由题意知,费用的多少跟购买办公室的数量有关,因此可根据题意设出的办公桌数量x张,分别写出两个家具店所需费用的函数关系式,建立函数模型,然后作比较,分y1>y2,y1=y2,y1<y2讨论.
解:解法1:(1)(解析法)根据题意得,当x>10时,y1=225×10+(x-10)×225×0.8=180x+450,y2=225×0.9x=202.5x;当x≤10时,y1=225x,y2=225×0.9x=202.5x;(2)由(1)可知当x≤10时,去乙店购买合算.当x>10时,若y1>y2,则去乙店购买合算,即180x+450>202.5x,解得x<20;若y1=y2,则去甲、乙两店收费相同,即180x+450=202.5x,解得x=20;若y1<y2,则去甲店购买合算,即180x+450<202.5x,解得x>20.答:该校购买办公桌少于20张时,去乙店购买合算;该校购买办公桌20张时,甲、乙两店收费相同;该校购买办公桌多于20张时,去甲店购买合算.
解法2:(图象法)(1)同解法1.(2)当x≤10时同解法1,当x>10时,设去甲、乙两店购买的费用差为y元,则y=y1-y2=(180x+450)-202.5x=-22.5x+450.画出一次函数y=-22.5x+450的图象如图所示,它与x轴的交点为(20,0),由图象可知:①当x<20时,y>0,即y1>y2,去乙店购买合算;②当x=20时,y=0,即y1=y2,甲、乙两店费用相同;③当x>20时,y<0,即y1<y2,去甲店购买合算.答:该校购买办公桌少于20张时,去乙店购买合算;该校购买办公桌20张时,甲、乙两店费用相同;该校购买办公桌多于20张时,去甲店购买合算.
A
A
(1,0)
x<3
解:画图略;(1)x>2
(2)-1≤x≤5
理解函数的概念,并从中初步体会一元一次不等式与一次函数的内在联系.通过具体问题初步体会一次函数的变化规律与一元一次不等式的解集的联系.使学生从整体上认识不等式,感受函数、方程、不等式的作用.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
